Towards a Fully Nonlinear Sharp Sobolev Trace Inequality

Jeffrey S.Case and Yi Wang ∗

1 109 McAllister Building,Penn State University,University Park,PA 16802

2 Department of Mathematics,Johns Hopkins University,Baltimore,MD 21218.

Abstract. We classify local minimizers among all conformally flat metrics in the Euclidean(n+1)-ball,n=4 or n=5,for which the boundary has unit volume,subject to an ellipticity assumption. We also classify local minimizers of the analogous functional in the critical dimension n+1=4. If minimizers exist, this implies a fully nonlinear sharp Sobolev trace inequality. Our proof is an adaptation of the Frank–Lieb proof of the sharp Sobolev inequality, and in particular does not rely on symmetrization or Obata-type arguments.

Key words: conformally covariant operator; boundary operator; σk-curvature;Sobolev trace inequality;fully nonlinear PDE.

1 Introduction

The first sharp Sobolev trace inequality was proven by Escobar[21]. In geometric terms,he showed that if g is any conformally flat metric on the Euclidean ball Bn+1⊂Rn+1,n>1,of radius one,then

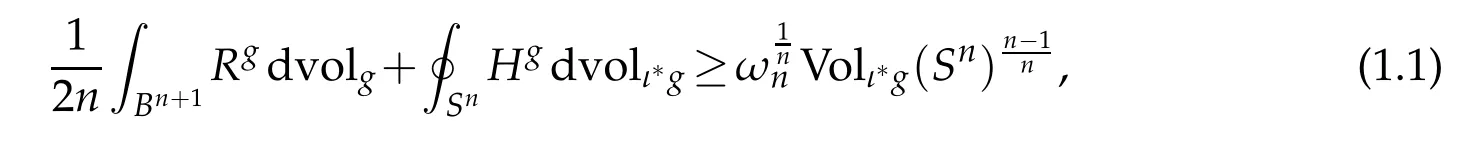
where ωnis the volume of the standard n-sphere, ι: Sn→Bn+1is the inclusion of Sn=∂Bn+1,and Hgis the mean curvature of Sninduced by g,with the convention that Snhas mean curvature 1 with respect to the standard metric. Moreover,he showed that equality holds in (1.1) if and only if g is flat. His proof relies on an Obata-type argument which classifies all conformally flat,scalar flat metrics g on the ball for which the boundary has constant mean curvature. The inequality (1.1) plays a crucial role in studying a version of the boundary Yamabe problem;see[2,22,31–33]and references therein.

In analytic terms,Eq. (1.1)states that

Initial studies of the σk-curvature involved constructing minimizers of the total σkcurvature functional among all volume-normalized metrics in the positive k-cone (e.g.[29, 30, 37]). In the critical case of dimension four, Chang, Gursky and Yang [13] noted that one could instead work in the positive 1-cone provided the total σ2-curvature was positive.Later studies(e.g.[26,27,36])generalized this to show that one can minimize in the positive (k−1)-cone under a suitable integral assumption. For example, combining results of Guan and Wang[28]and Ge and Wang[26]yields sharp fully nonlinear Sobolev inequalities of closed n-spheres,n>4,stated in terms of the σ2-curvature and the positive 1-cone. Note that Obata’s argument generalizes to prove that any conformally flat metric of constant σk-curvature on the sphere has constant sectional curvature, subject to the above ellipticity condition[14,38].

Given k∈N, S.Chen[18]defined the Hk-curvature of the boundary of a Riemannian manifold(Xn+1,g)in terms of elementary symmetric functions of the Schouten tensor of the interior and the second fundamental form of the boundary. The key points are that H1is the mean curvature;, g∈[g0],when written in terms of a fixed boundary metric g0,depends only on the tangential two-jet of u and the normal derivative of u along the boundary;and,provided k≤2 or g is locally conformally flat,

In the critical dimension n+1=2k,one instead expects a Lebedev–Milin-type inequality stated in terms of the functional Fk(cf.[1, 5,35]). This is analogous to sharp Onofritype inequalities known on closed spheres(cf.[16,17,28,34,35]).

with equality if and only if g is flat.

Theorem 1.1. Let(Bn+1,dx2),n=4 or 5,be the closed unit ball in Euclidean(n+1)-space and suppose that g ∈C1is a local minimizer of S2: V →R. Then g=dx2up to the action of the conformal group of Bn+1.

In comparison with our previous work [12], Theorem 1.1 removes the pinching assumption but imposes the stronger assumption that g∈C1is a local minimizer of S2: V→R,rather than just a critical point. We expect that the dimensional assumption n≤5 can be removed.

Theorem 1.2. Let(B4,dx2)be the closed unit ball in Euclidean four-space. Suppose that g∈C1is a local minimizer of F2: V →R.Then g=dx2up to the action of the conformal group of B4.

We remark that in Theorem 1.1 and Theorem 1.2 we assume g is a local minimizer of V as our proofs are based on the first and the second variation formulas. We also require g∈C1for ellipticity. We do not know whether a local minimizer of S2(or F2)on V ∩C1is a local minimizer on V,but hope to investigate this later.

We prove Theorem 1.1 and Theorem 1.2 by adapting the rearrangement-free proof by Frank and Lieb[23]of Aubin’s sharp Sobolev inequality[3]. Indeed,this same technique gives a new proof of (1.1); see Subsection 5.1 for details. To the best of our knowledge,this is the first time the Frank–Lieb argument has been employed on manifolds with boundary.

The Frank–Lieb argument exploits conformal covariance and a nice formula for the commutator of the conformal Laplacian on the sphere with a first spherical harmonic;similar properties allow Frank and Lieb to also prove sharp Sobolev inequalities on the CR spheres[24]. Our proof also exploits conformal invariance and nice commutator formulae,this time both in the interior and on the boundary of Bn+1. An intriguing question is whether our proofs can be adapted to CR manifolds.

In another direction, we verify Conjecture 1.1 and Conjecture 1.2 when k=2 with nonsharp constants.

Theorem 1.3. Let (Bn+1,dx2), n>3, be the closed unit ball in Euclidean (n+1)-space. Then there exists some constant C>0 such that

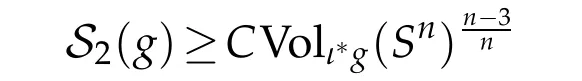
for all g∈C1.

Theorem 1.4. Let (B4,dx2) be the closed unit ball in Euclidean four-space. Then there exists some constant C>0 such that,

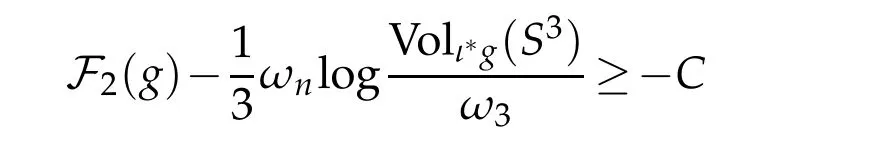
for all metric g∈C1,

This article is organized as follows. In Section 2 we collect some useful background information on the σ2-and H2-curvatures. In Section 3 we prove Theorem 1.3 and Theorem 1.4. In Section 4 we explain how conformal invariance and the assumption of a local minimizer are used in the Frank–Lieb argument. In Section 5 we give a new proof of(1.1)and prove Theorem 1.1 and Theorem 1.2.

2 Background

Let(Xn+1,g)be a Riemannian manifold. The Schouten tensor is

The first Newton tensor T1is the section of S2T∗X given by

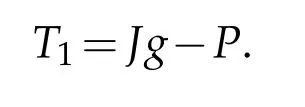
A consequence of G˚arding’s work on hyperbolic polynomials [25] is that if g is in the positive elliptic 2-cone,

then T1>0;see[9]. Moreover,if then T1≥0. The importance of this observation comes from the conformal transformation formula for the σ2-curvature:

which are differential in each of their inputs. These operators have two key properties.First,they are conformally covariant: If gu=u8

n−3g,then

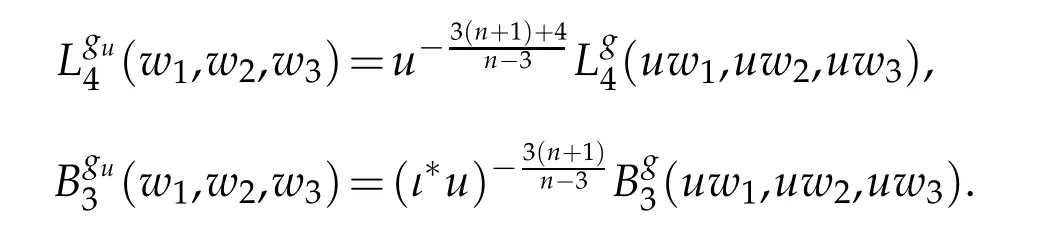
Second,the pair(L4;B3)is formally self-adjoint: The map

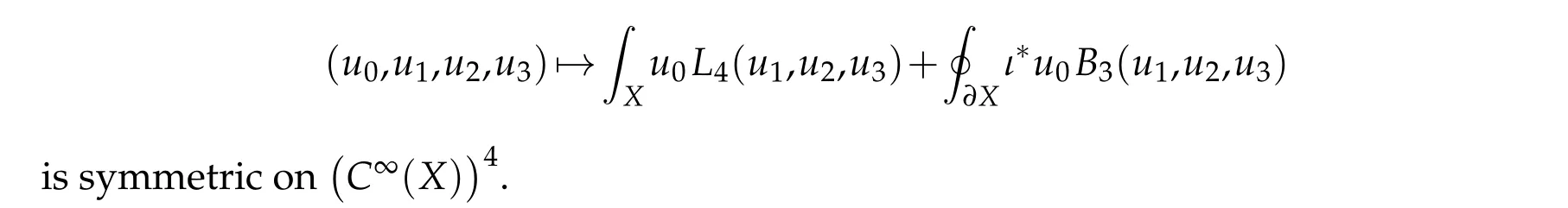
We require the following explicit formula for L4and B3under certain geometric conditions:

Lemma 2.1. Let(Xn+1,g)be a Ricci flat manifold. Then

where the fourth equality also uses the assumption that g is Ricci flat.

Lemma 2.2. Let (Xn+1,g) be a Ricci flat manifold with umbilic boundary of constant mean curvature H. Then

Proof. On the one hand,the conformal transformation law for the mean curvature implies that

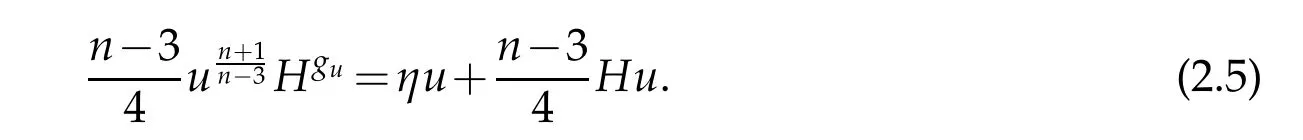
On the other hand,the assumptions that g is Ricci flat and ∂X is umbilic imply,using(2.4),that

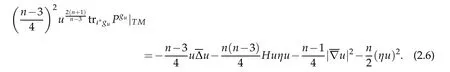
Combining these formulae with the definition of B3yields the desired result.

It will be useful to express L4and B3in alternative forms. To that end,we introduce some operators.

Definition 2.1. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space,n/=3. We define σ1: C∞(B)→C∞(B),T1: C∞(B)→C∞(B;S2T∗B),and H: C∞(B)→C∞(∂B)by

As suggested by our notation, the point of these operators is that they are closely related to the corresponding geometric objects defined with respect to the metric gu:=dx2,but with the extra benefit of being polynomial in u and its covariant derivatives.The relations to geometric objects defined with respect to guare given by the following lemma. This also indicates how to extend the definitions of σ1, T1, and H to general manifolds with boundary.

Lemma 2.3. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space. Then

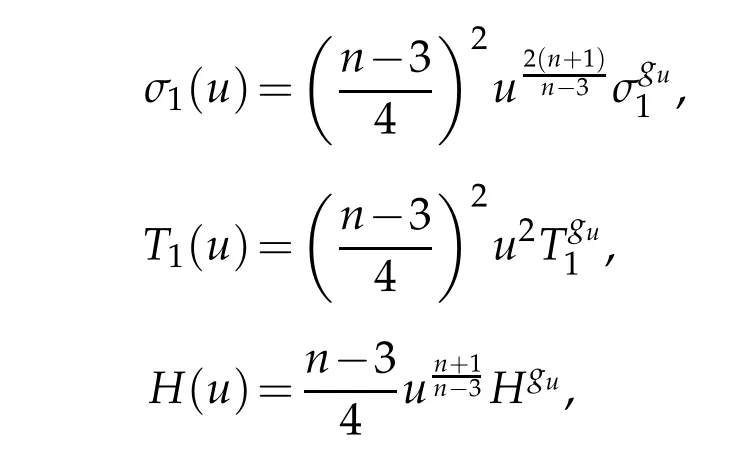
where gu:=dx2. In particular,each of σ1,T1,and H is conformally covariant.

Proof. The equations for σ1(u)and T1(u)follow from(2.4). The equation for H(u)follows from(2.5).

A useful corollary of Lemma 2.3 is the following expression for T1(u)(η,η).

Corollary 2.1. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space. Then

Proof. On the one hand,Lemma 2.3 implies that

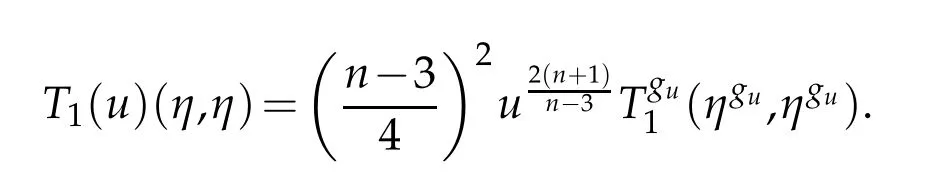
On the other hand,it holds that

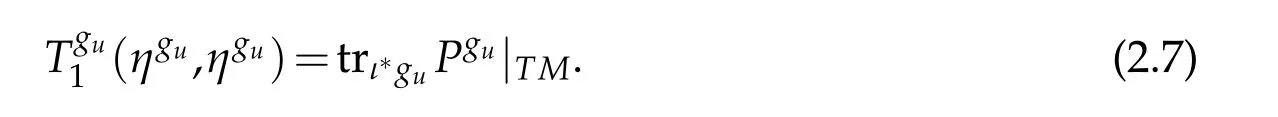
Applying(2.6)yields the desired conclusion.

Lemma 2.3 also implies the following useful formulas for L4and B3.

Proposition 2.1. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space. Then

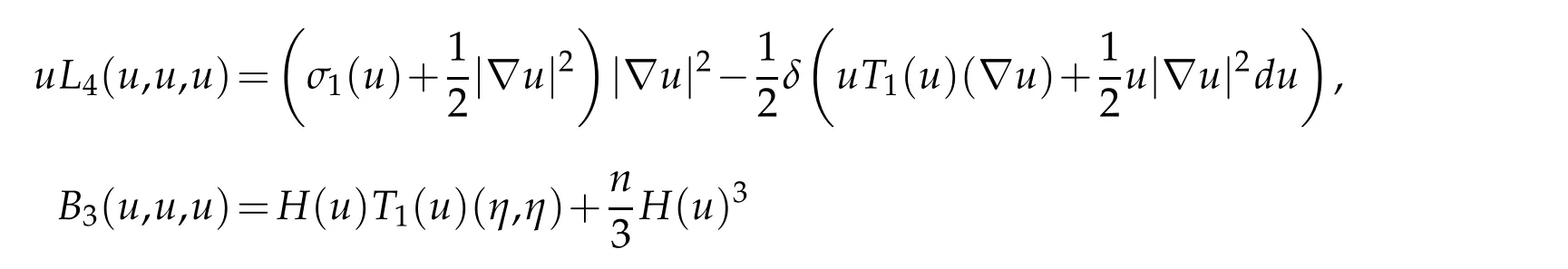
for all u∈C∞(B).

Combining this with(2.9)yields the formula for uL4(u,u,u).

2.1 The four-dimensional case

In dimension four, the behavior of σ2and H2under conformal change of metric is also controlled by conformally covariant polydifferential operators. The following result can also be derived from Lemma 2.1 and Lemma 2.2 by analytic continuation in the dimension.See[11]for a general discussion on closed manifolds.

Then

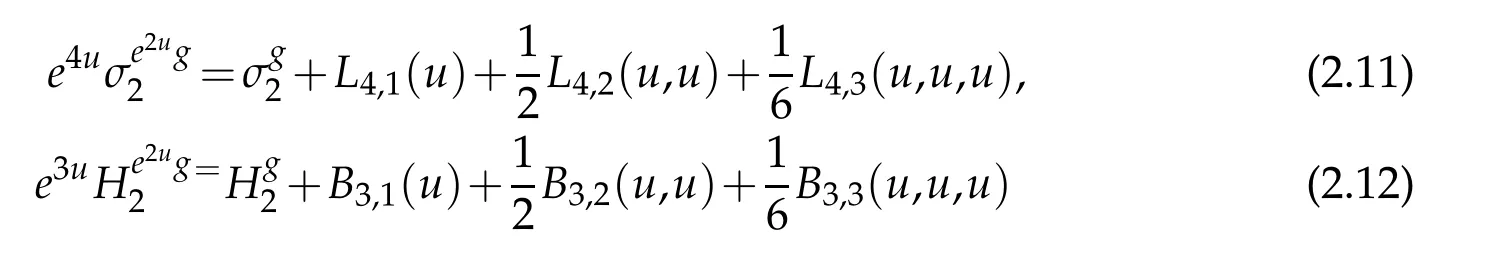
for all u∈C∞(X).

Proof. We directly compute that

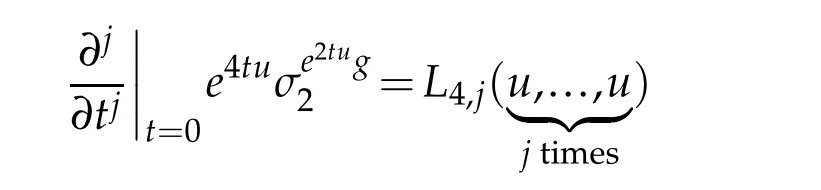
for all integers 1≤j≤4,with the convention L4,4=0. Integrating along the path te2tug,t∈[0,1],yields(2.11).

Since ∂X is umbilic,we directly compute that

for all integers 1≤j≤4,with the convention B3,4=0. Integrating along the path t2tug,t∈[0,1],yields(2.12).

One important property of the operators L4,jand B3,jis their transformation under conformal change of metrics,generalizing(2.11)and(2.12),respectively.

Corollary 2.2. Let (X4,g) be a Riemannian manifold with umbilic boundary. For any integer 1≤j≤3,it holds that

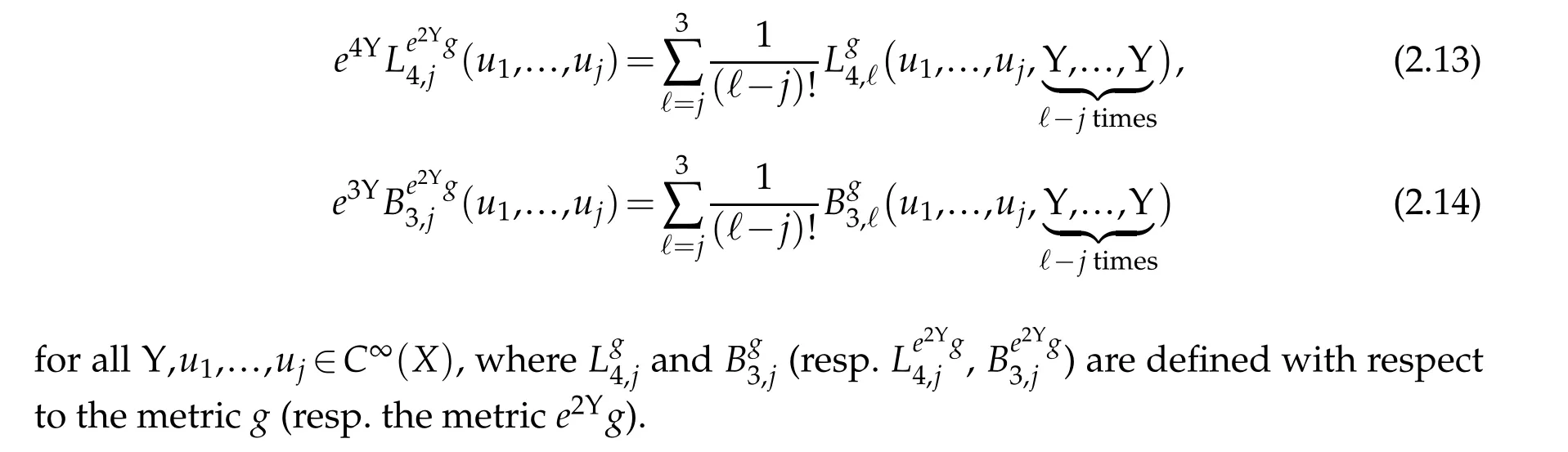
Remark 2.1. One can easily show that Lemma 2.4 and Corollary 2.2 also hold in the nonumbilic case with only a slight change to the definition of B3,1.

Proof. Using(2.11)to compute e4(Υ+tu)in two ways yields

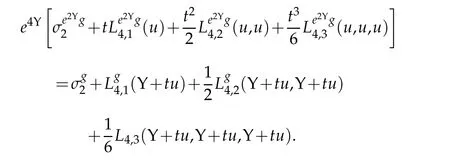
Equating coefficients of t and polarizing yields (2.13). The verification of (2.14) follows similarly from(2.12).

Another important property of the operators L4,jand B3,jis that the pairs (L3,j;B3,j)are formally self-adjoint;i.e.the maps

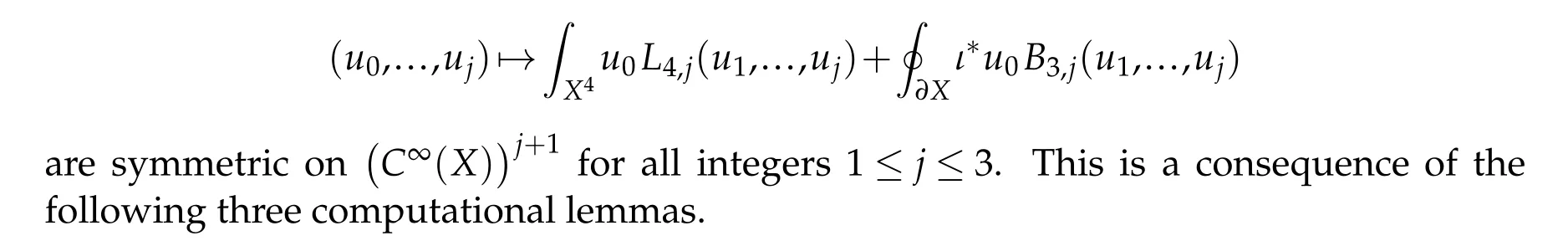
Lemma 2.5. Let(X4,g)be a compact Riemannian manifold with umbilic boundary. Then

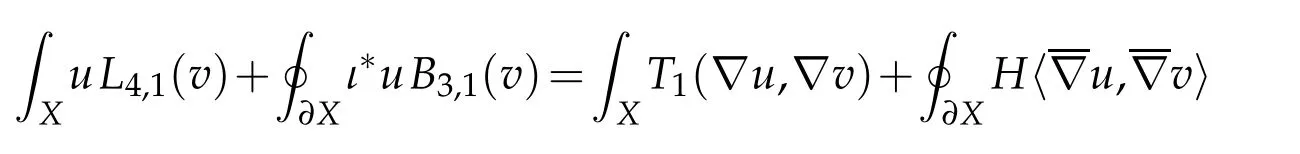
for all u,v∈C∞(X).

Proof. It directly follows from Lemma 2.4 that

Since ∂X is umbilic, T1(η,∇v)=〈∇H,∇v〉(see[10,Lemma 2.1]). The conclusion readily follows.

Lemma 2.6. Let(X4,g)be a compact Riemannian manifold with umbilic boundary. Then

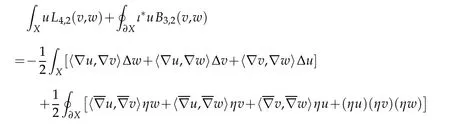
for all u,v,w∈C∞(X).

Proof. It follows directly from Lemma 2.4 that

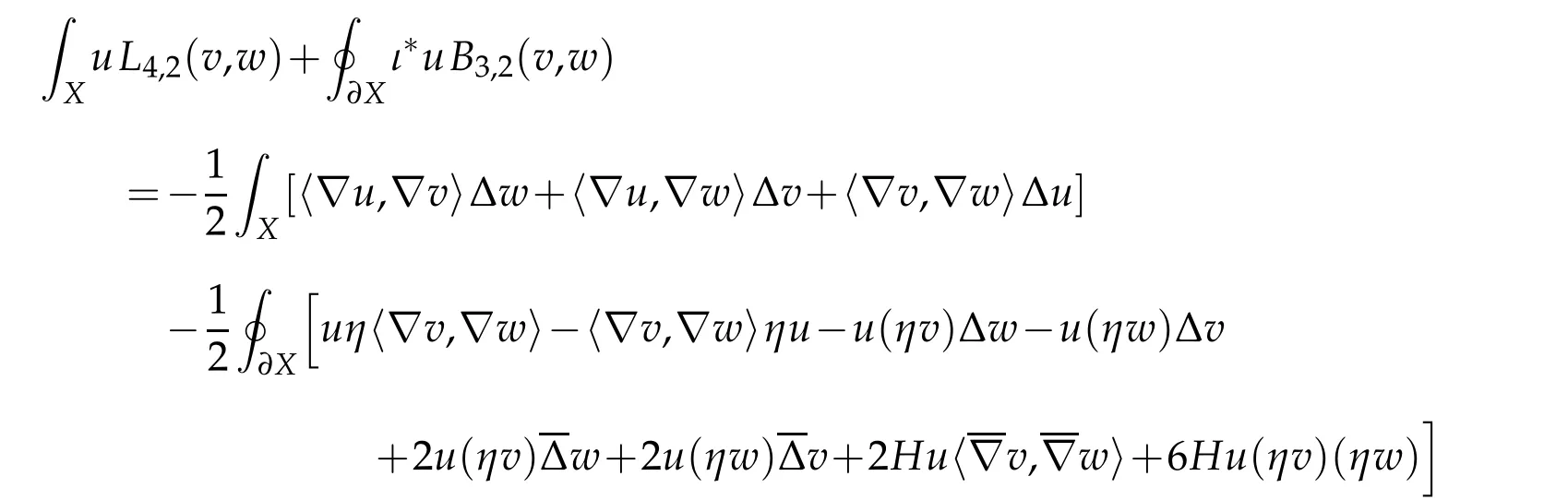
Since ∂X is umbilic,

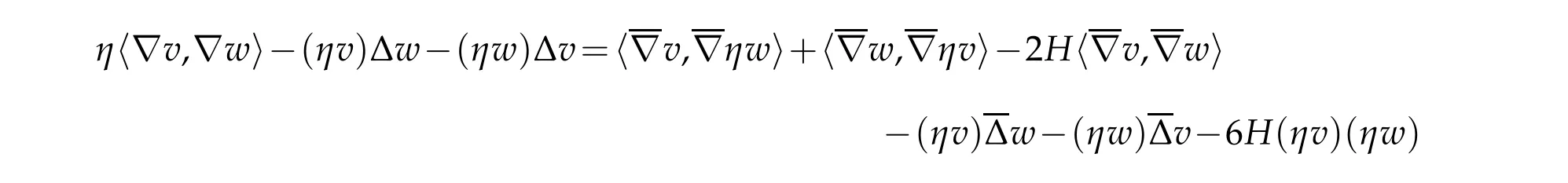
(see[10,Lemma 2.3]). The conclusion readily follows.

Lemma 2.7. Let(X4,g)be a compact Riemannian manifold with umbilic boundary. Then

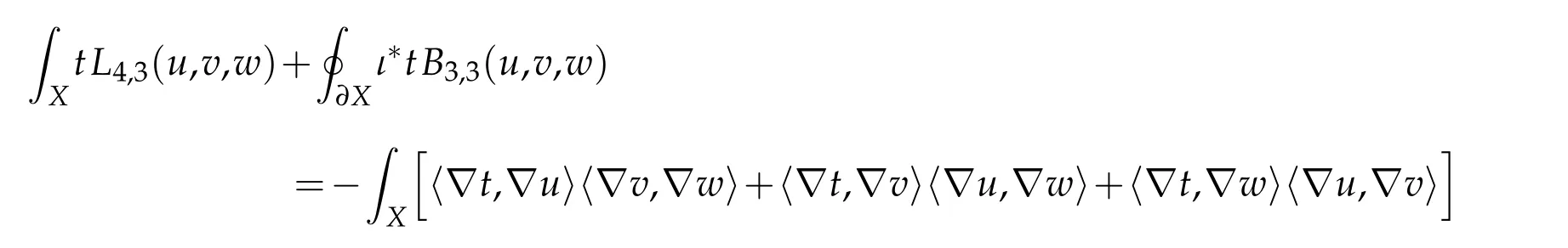
for all t,u,v,w∈C∞(X).

Proof. This follows directly from Lemma 2.4.

3 A non-sharp fully nonlinear Sobolev trace inequality

The remainder of this article is concerned with the functional

defined with respect to the unit ball in Euclidean (n+1)-space and its analogue when n=3. Note that,by the conformal invariance of L4and B3,

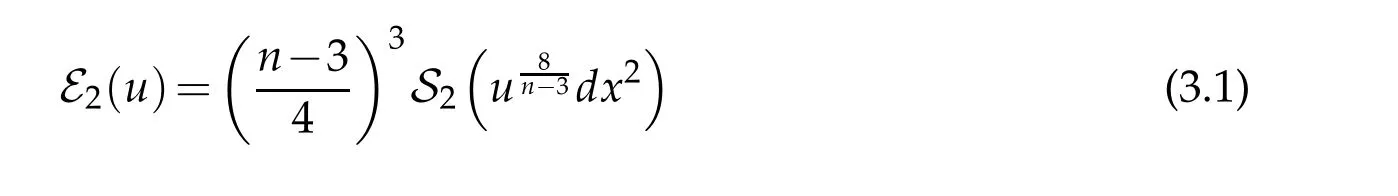
for all positive u ∈C∞(B). The main result of this section is the following (non-sharp)fully nonlinear Sobolev trace inequality in

Note that C1equals the set(1.5)under the correspondence u～=u8

n−3dx2.Recall the statement of Theorem 1.3. We note that it is equivalent to the following theorem.

Theorem 3.1. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space. Then

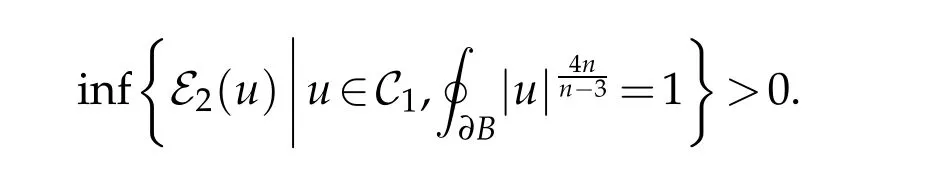
Proof. We first derive a general formula for E4(u)making no assumptions on u. Proposition 2.1 implies that

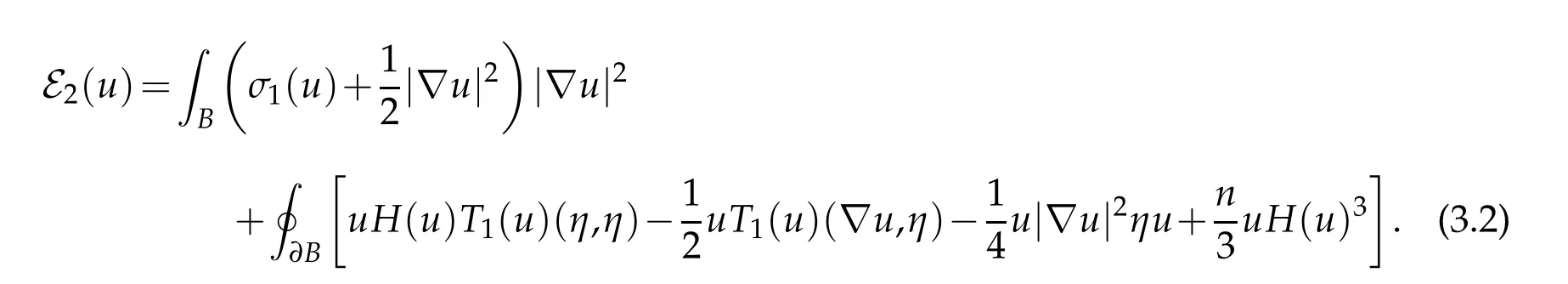
To simplify this,first note that

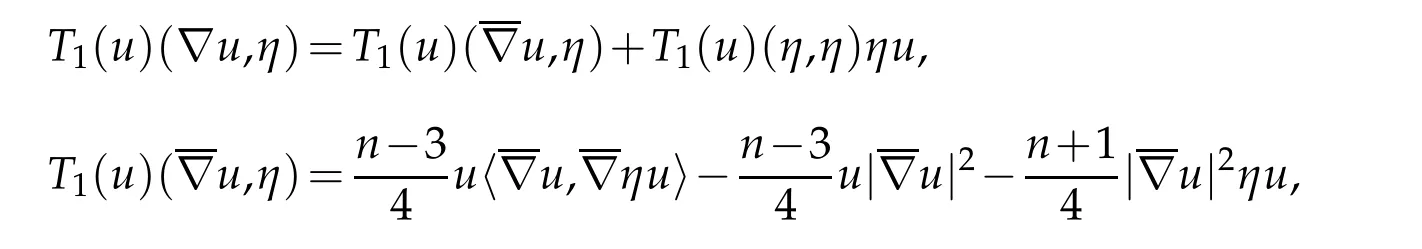
where the second equality uses Definition 2.1 and the fact that ∂B is umbilic with second fundamental form II=ι∗dx2. We conclude that

where the second equality uses Corollary 2.1. Combining this with (3.2) and using the definition of H(u)yields

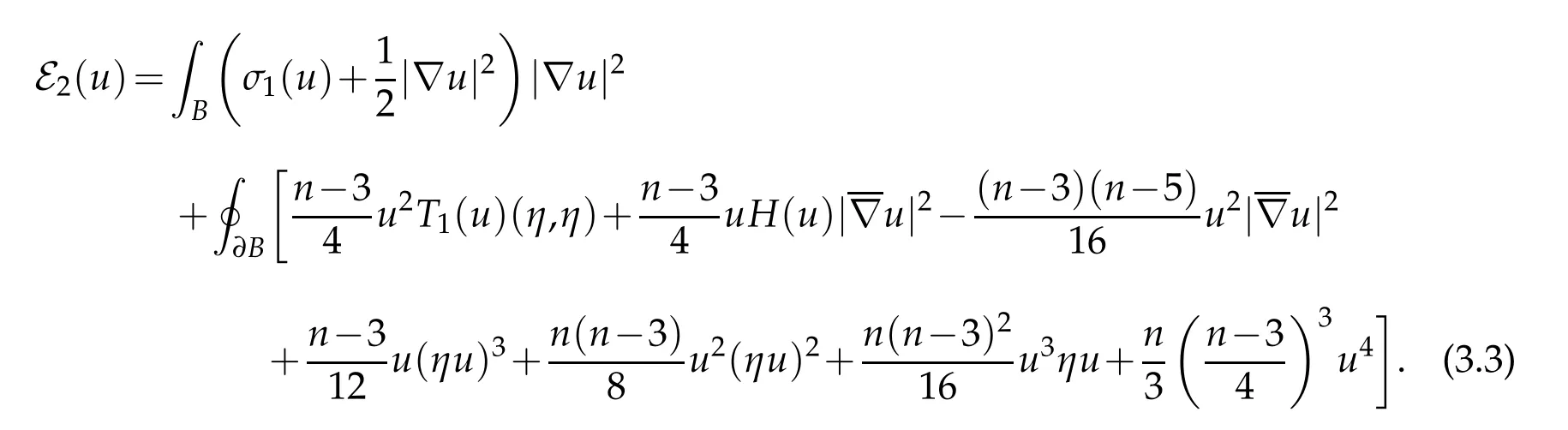
Using Corollary 2.1 again yields Combining this with(3.3)yields

3.1 The four dimensional case.

We omit the superscript g when the background metric is clear from context. We require the following equivalent formula for F2.

Lemma 3.1. Let(X4,g)be a compact Riemannian manifold with umbilic boundary. Then

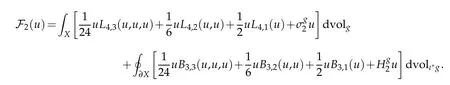
Proof. Lemma 2.4 immediately implies that

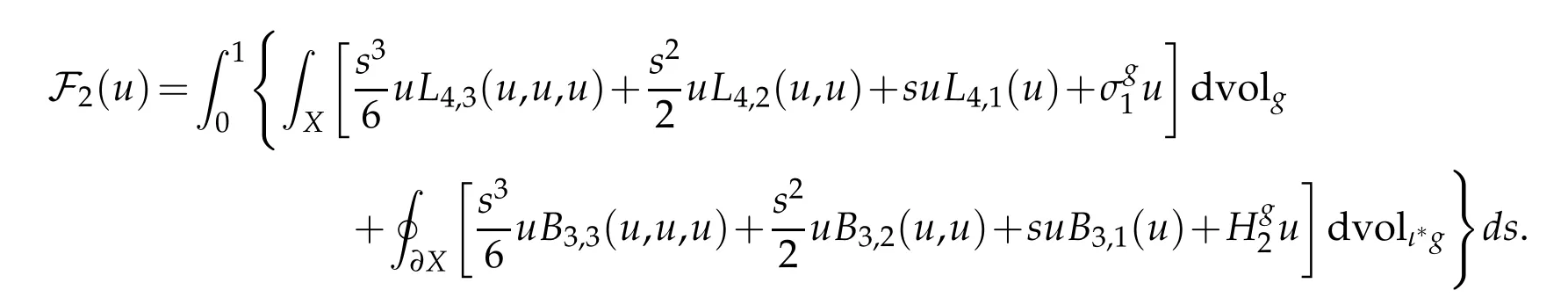
The conclusion readily follows.

The functional F2is conformally invariant,in the sense that it satisfies the following cocycle condition(cf.[7]).

Lemma 3.2. Let(X4,g)be a compact Riemannian manifold with umbilic boundary. Then

for all u,v∈C∞(X).

Proof. This follows directly from Corollary 2.1 and Lemma 3.1.

Adapting an argument of Chang and Yang[16]yields the following specialization of Lemma 3.2 to the Euclidean four-ball.

Corollary 3.1. Let(B4,dx2)be the closed unit ball in Euclidean four-space. Then

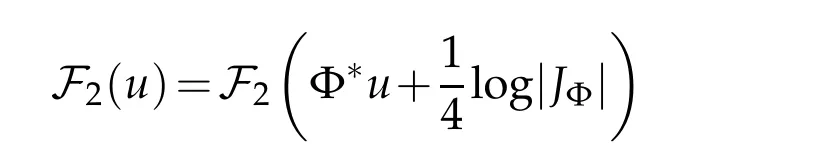
for all u∈C∞(B)and all Φ∈Conf(B4;S3),the group of conformal diffeomorphisms of B4which fix the boundary,where|JΦ|is the Jacobian determinant,dvolΦ∗dx2=|JΦ|dvoldx2.

Proof. First observe that(3.7)yields

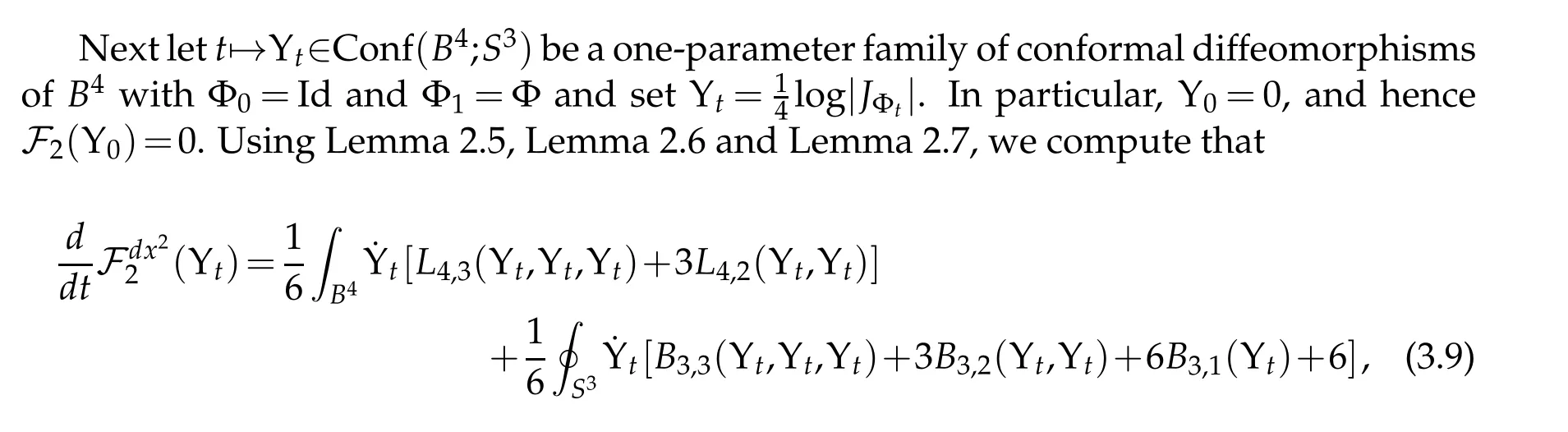
for all t∈[0,1]. Inserting this into(3.9)yields

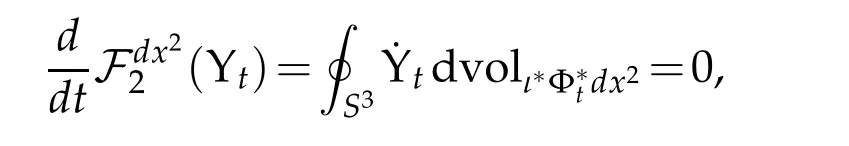
where the last equality uses the fact that VolΦ∗tdx2(S3)is constant. In particular,

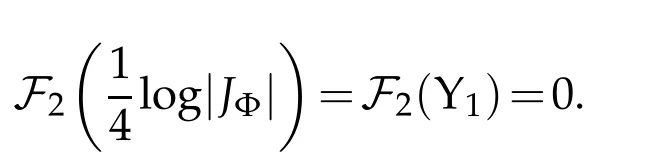
Inserting this into(3.8)yields the desired conclusion.

It is more useful to write F2(u) after integration by parts. Given our focus in this article,we restrict our attention to the unit ball in Euclidean four-space.

Lemma 3.3. Let(B4,dx2)be the closed unit ball in Euclidean four-space. Then

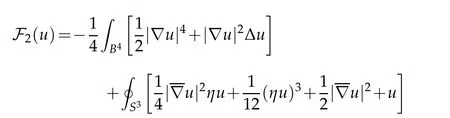
for all u∈C∞(B).

Proof. First observe that dx2is Ricci flat,and hence Tdx21 =0,and S3=∂B4is umbilic and has constant mean curvature H=1. The conclusion follows from Lemma 2.5,Lemma 2.6,Lemma 2.7 and Lemma 3.1.

To establish our Lebedev–Milin-type inequality,we again need to restrict to the conformal metrics of nonnegative scalar curvature and positive mean curvature. To that end,define σ1: C∞(B4)→C∞(B4)and H: C∞(B4)→C∞(S3)by

Note that

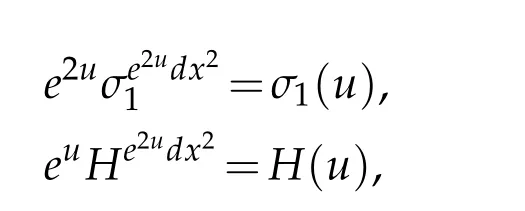
justifying our notation. Set

Note that C1equals the set(1.5)under the correspondence u～=e2udx2used in(3.6).

Our Lebedev–Milin-type inequality establishes a uniform lower bound on the functional G2: C1→R,

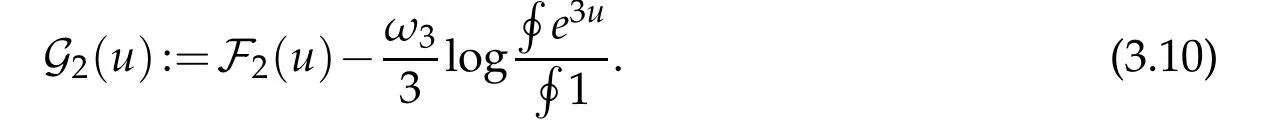
Among the key properties of G2are that it is scale in and conformally invariant. These properties allow us study G2in the subspace S∩C1,where

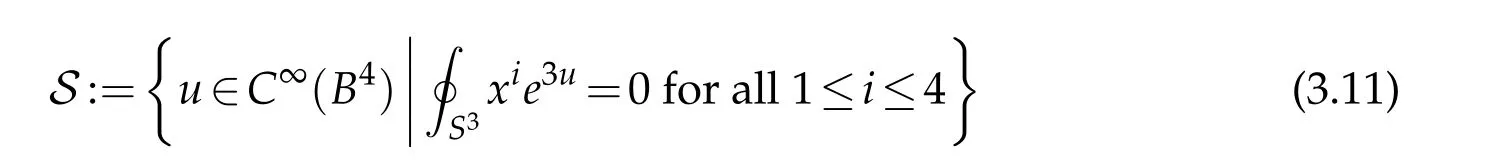
and x1,...,x4denote the standard Cartesian coordinates on B4. Our Lebedev–Milin-type inequality then follows from an improved Moser–Trudinger trace inequality for functions u∈S involving the L4-norm of ∇u in the interior(cf.[4]). The remainder of this subsection is devoted to explaining these points.

We begin by establishing the conformal and scale invariance of G2.

Lemma 3.4. Let(B4,dx2)be the closed unit ball in Euclidean four-space, let c∈R be constant,and let Φ∈Conf(B4;S3)be a conformal diffeomorphism of B4. Then

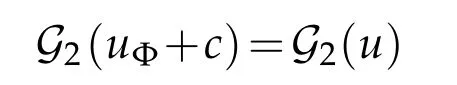
for all u∈C∞(B4),where

Proof. It is clear that G2(u)=G2(u+c)for all u∈C∞(M)and all c∈R. Since Φ is conformal,we see that dvolΦ∗ι∗dx2=|JΦ|3/4dvolι∗dx2. Thus,by change of variables,

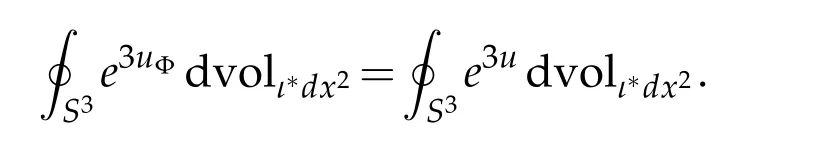
Combining this display with Corollary 3.1 yields G2(uΦ)=G2(u). The desired conclusion follows from these two observations.

Lemma 3.4 implies that the infima of G2: C1→R and G2: S∩C1→R agree.

Lemma 3.5. Let (B4,dx2) be the closed unit ball in Euclidean four-space and let u ∈C∞(M).Then there is a Φ∈Conf(B4;S3)such that uΦ∈S,where uΦis defined by(3.12). In particular,

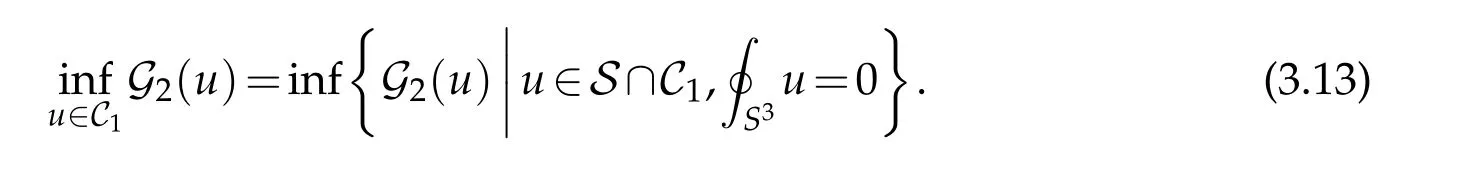
Proof. Applying [23, Lemma B.1]x to the function e3u◦ι on ∂B yields an elementΦ ∈Conf(S3)such thatu:=u◦ι◦Φ+13log|JΦ|satisfies

When restricted to elements of the set(3.11)of balanced functions,the constant 128ω3/81 in Proposition 3.1 improves by a factor of almost two. A similar phenomenon for closed manifolds was first observed by Aubin [4]. Our proof below adapts ideas of Aubin[4]and of Branson,Chang and Yang[6].

Proposition 3.2. Let (B4,dx2) be the closed unit ball in Euclidean four-space. For any ε>0,there is a constant C=C(ε)such that

Given an integer 1≤i≤4,denote

Combining(3.15)–(3.17),and(3.23)with suitable choices of η and ε1yields(3.14).

We are now able to prove our Lebedev–Milin-type inequality. Recall the statement of Theorem 1.4 and note that it is equivalent to the following form:

Theorem 3.2. Let(B4,dx2)be the closed unit ball in Euclidean four-space. Then

Proof. By Lemma 3.5,it suffices to prove that

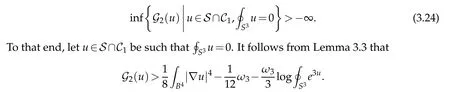
Applying Proposition 3.2 with ε=5/27 yields(3.24).

4 A spectral inequality at local minimizers

The Frank–Lieb argument[23]proving sharp Hardy–Littlewood–Sobolev inequalities begins with a spectral inequality satisfied by any local minimizer of the problem in question. When n≥4,we are concerned with the local minimizers of E2: V →R for

Now,since u is a critical point of E2: V →R,it satisfies

Combining this with(4.2)yields

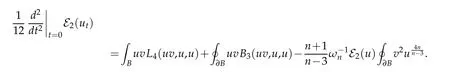
Now apply the assumption that u is a local minimizer of E2: V →R.

Define the commutators of L4and B3with multiplication operators by

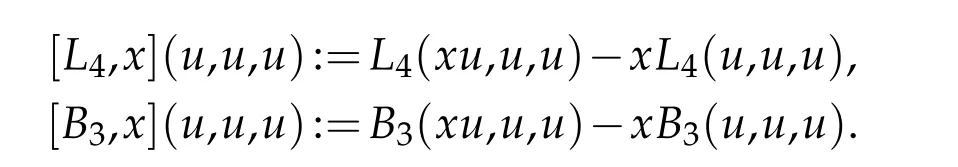
The core of the Frank–Lieb argument is contained in the following estimate.

Corollary 4.1. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space and let u be a local minimizer of E2: V →R. Suppose additionally that

The conclusion now follows from(4.3)and the definitions of the commutators.

One typically calls functions u which satisfy (4.4) balanced. It is well-known [15,23]that this condition can always be achieved by a suitable M¨obius transformation. For conformally covariant problems, this means that local minimizers, if they exist,can always be taken to be balanced. Specifically:

Proposition 4.2. Let(Bn+1,dx2)be the closed unit ball in Euclidean(n+1)-space and let u be a local minimizer of E2: V →R. Then there is a Φ∈Conf(Bn+1;Sn)such that

is a balanced local minimizer of E2: V →R.

Proof. First observe that,by change of variables,u∈V if and only if uΦ∈V. Moreover,by the diffeomorphism invariance of E2,we see that

for all u∈C∞(B)and all Φ∈Conf(Bn+1;Sn). In fact,Eq. (3.1)implies that

4.1 The four-dimensional case

When n=3, the relevant functional G2is (3.10). This functional is scale invariant (see Lemma 3.4), so there is no need to impose an additional volume normalization. The analogue of Proposition 4.1 when n=3 is as follows:

Proposition 4.3. Let(B4,dx2)be the closed unit ball in Euclidean four-space and let u be a local minimizer of G2: C∞(B)→R. Then

for all v∈C∞(B)such that

Proof. It follows from Lemma 2.5,Lemma 2.6 and Lemma 2.7 that

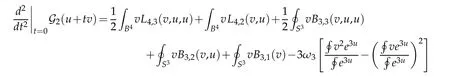
for all u,v ∈C∞(B). The conclusion follows by assuming that u is a local minimizer of G2: C∞(B)→R and v satisfies(4.7).

Note that the operators L4,j, B3,j, j=1,2,3,annihilate constants,in the sense that they give the zero function if at least one of their inputs is constant. This will make it relatively easy to apply the following immediate consequence of Proposition 4.3 for balanced minimizers.

Corollary 4.2. Let (B4,dx2) be the closed unit ball in Euclidean four-space and let u be a local minimizer of G2: C∞(B)→R. Suppose additionally that u ∈S for S as in (3.11).Then

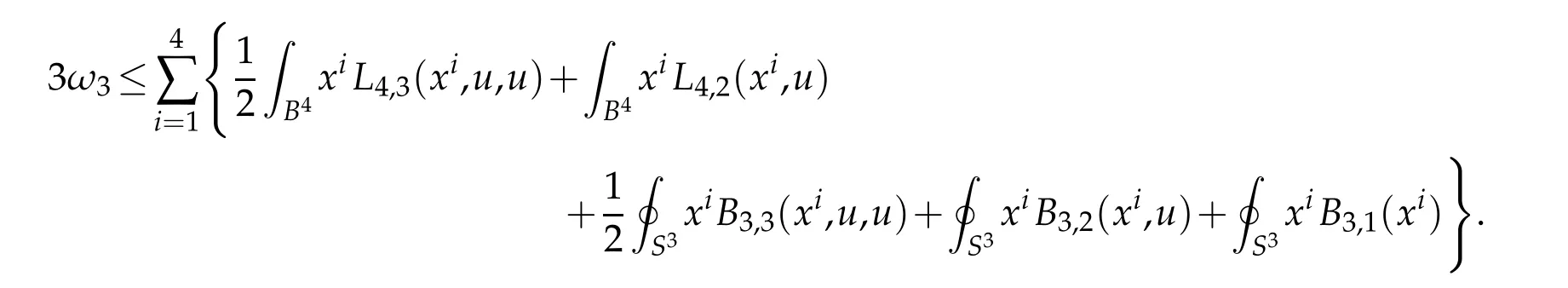
As in the higher-dimensional case(cf.Proposition 4.2),one can always assume that a local minimizer of G2: C∞(B)→R satisfies the balancing condition u∈S.

Proposition 4.4. Let(B4,dx2)be the closed unit ball in Euclidean four-space and let u be a local minimizer of G2: C∞(B)→R. Then there is a Φ ∈Conf(B4;S3) such that uΦ, as defined by(3.12),is a local minimizer of G2: C∞(B)→R and satisfies uΦ∈S.

Proof. Let u be a local minimizer of G2: C∞(B)→R. Lemma 3.5 yields a Φ∈Conf(B4;S3)such that uΦ∈S. Lemma 3.4 implies that G2(uΦ)=G2(u). It follows that uΦis a balanced local minimizer of G2: C∞(B)→R.

5 Classification of local minimizers

As indicated in Section 4, it remains to compute the commutators [L4,xi] and [B3,xi].To illustrate this strategy in a simple case, we first give a new proof that the only local minimizers of Escobar’s sharp Sobolev trace inequality (1.2) are the constant functions and their images under the action of the conformal group.

5.1 Escobar’s functional

The analogue of Corollary 4 is that

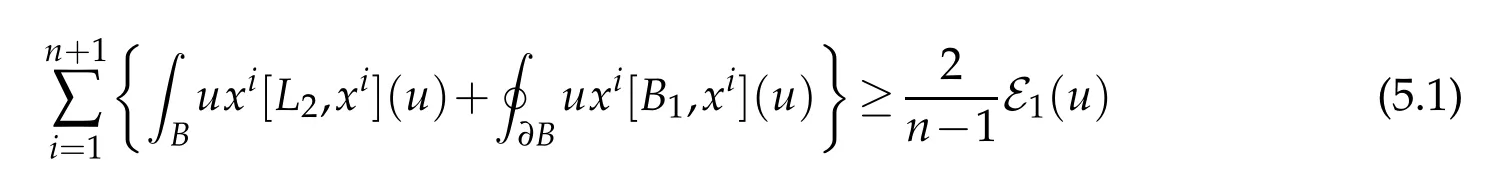
for all positive balanced local minimizers u of

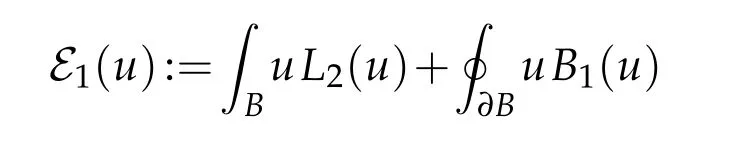
in the set

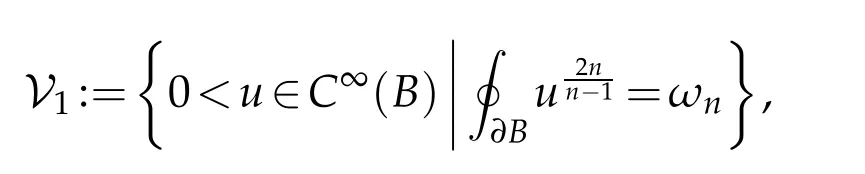
where a function u is balanced if

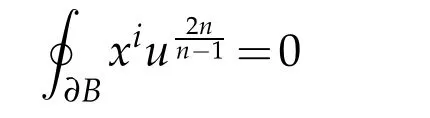
for all integers 1≤i≤n+1. Here we use the standard correspondenceubetween functions on Bn+1and conformally flat metrics.

It is straightforward to compute that

Inserting this into(5.1)and using the formula

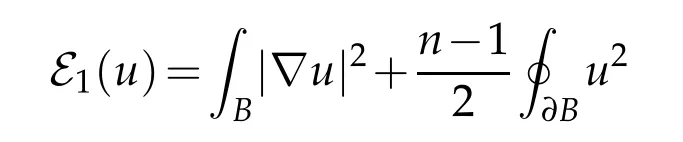
yields

where r2is the squared distance from the origin. Since u is a local minimizer of E1: V1→R,it satisfies L2u=0. Integrating this against(1−r2)u yields

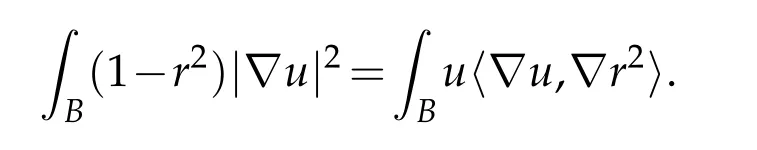
Combining this with(5.2)yields

Therefore u is constant.

5.2 The functional E2

Our objective is to classify local minimizers of the functional

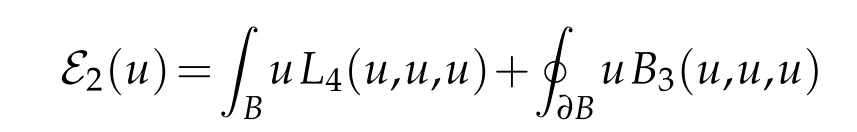
defined on the set

We assume our minimizers are in the nonnegative cone

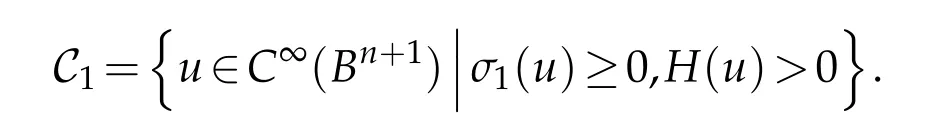
Note that local minimizers of E2: V →R are such that the first variation vanishes and the second variation is nonnegative.

Our first task is to compute the commutators[L4,xi]and[B3,xi]. This is accomplished in the following two lemmas.

Lemma 5.1. Let Bn+1be the closed unit ball in (n+1)-dimensional Euclidean space and let x denote a Cartesian coordinate in Rn+1. Then

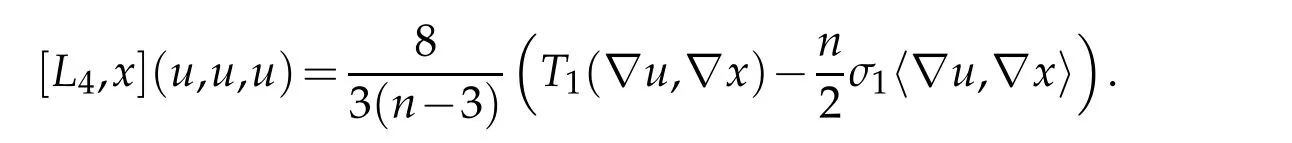
Proof. It follows immediately from Lemma 2.1 that

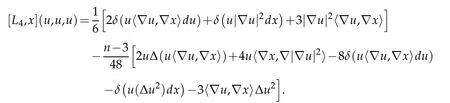
Expanding this out yields

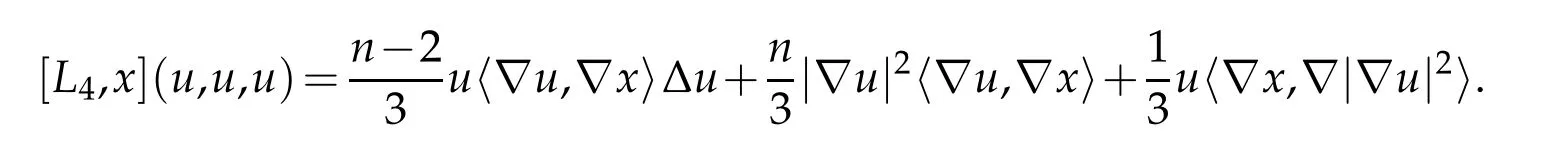
Rewriting this using Definition 2.1 yields the desired result.

Lemma 5.2. Let Bn+1be the closed unit ball in (n+1)-dimensional Euclidean space and let x denote a Cartesian coordinate in Rn+1. Then

Proof. Recall that ∂B is umbilic with constant mean curvature 1. It follows from Lemma 2.2 that

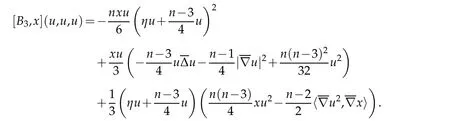
The final conclusion follows from Definition 2.1 and Corollary 2.1.

Analogous to Subsection 5.1,the application of the commutator formula in Lemma 5.1 will produce an interior integral involving T1(∇u,∇r2). Our second task is to find a useful estimate for this integral.

Lemma 5.3. Let(Bn+1,dx2)be the closed unit ball in(n+1)-dimensional Euclidean space and let r2∈C∞(B)denote the squared-distance from the origin. Then

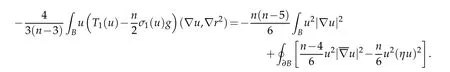
Proof. On the one hand,it follows from(2.8)and the identities ∇2r2=2dx2and trT1(u)=nσ1(u)that

On the other hand,it follows from Definition 2.1 that

Combining these displays yields

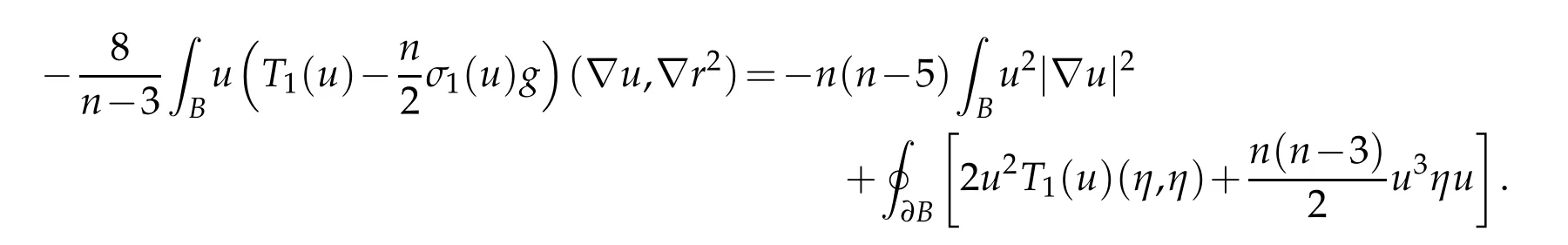
The final conclusion follows from(3.4).

We now have the ingredients in place to classify local minimizers of E2: V →R in dimension n+1≤6.

Proof of Theorem 1.1. Let u be a local minimizer of E2: V →R.Proposition 4.2 implies that,by using the action of Conf(Bn+1;Sn) if necessary, we may assume that u satisfies (4.4).

On the one hand,Corollary 4.1 states that

On the other hand,Lemma 5.1 and Lemma 5.2 imply that

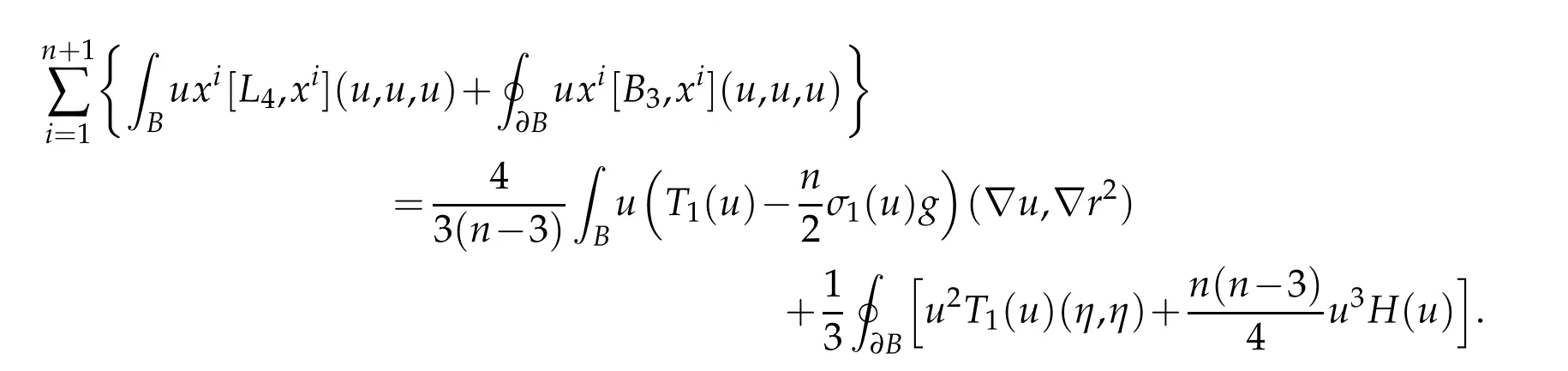
Combining these displays using(3.4)and Lemma 5.4 yields

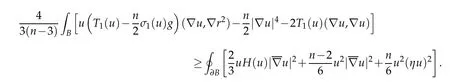
Combining this with Lemma 5.3 yields

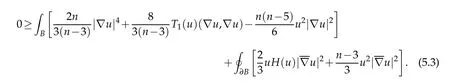
Since n ≤5, we see that the right-hand side is nonnegative, and hence equality holds in(5.3). Therefore u is constant.

5.3 The functional G2

We conclude by considering local minimizers u ∈C1of the functional G2: C∞(B4)→R defined by(3.10). Our first task is to compute L4,j(x,u,...,u)and B3,j(x,u,...,u).

Lemma 5.5. Let (B4,dx2) be the closed unit ball in Euclidean four-space and let x denote a Cartesian coordinate in R4. Then

for all u∈C∞(B).

Proof. By direct computation,

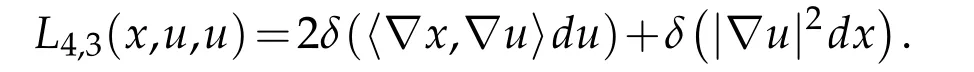
Expanding this using the fact ∇2x=0 yields(5.4). By direct computation again,

We deduce(5.5)from the facts that dx2is flat and ∇2x=0.

Lemma 5.6. Let (B4,dx2) be the closed unit ball in Euclidean four-space and let x denote a Cartesian coordinate in R4. Then

for all u∈C∞(B).

Proof. Recall that −∆x=3x. The conclusion follow by direct computation.

We obtain the following analogue of Lemma 5.3. Define the Γ(⊗2T∗S3)-valued differential operator T1by

Proof. First observe that

Therefore

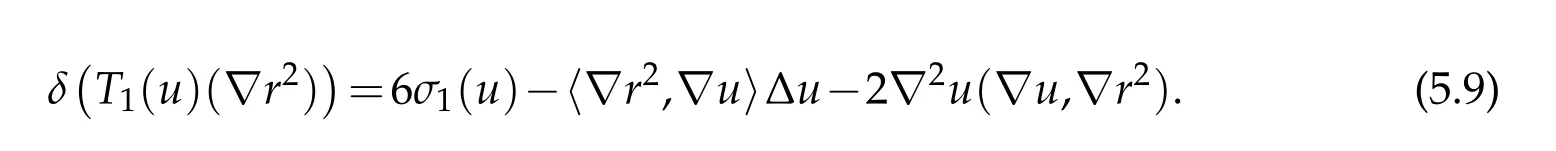
Second observe that

Combining these results with the Divergence Theorem yields the desired conclusion.

We now can classify local minimizers of G2: C∞(B4)→R which are in C1.

Proof of Theorem 1.2. Note that u ∈C∞(B4) is a local minimizer of G2: C∞(B)→R if and only if u+c is a local minimizer of F: V →R, where the constant c is chosen such that u+c∈V.

Let u ∈C1be a local minimizer of G2: C∞(B)→R. Proposition 4.4 implies that, by using the action of Conf(B4;S3) if necessary, we may assume that u ∈S. Combining Corollary 4.2,Lemma 5.5,Lemma 5.6 and(5.10)yields

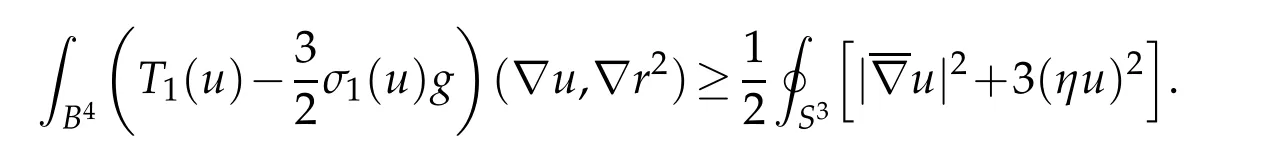
Combining this with Lemma 5.7 yields

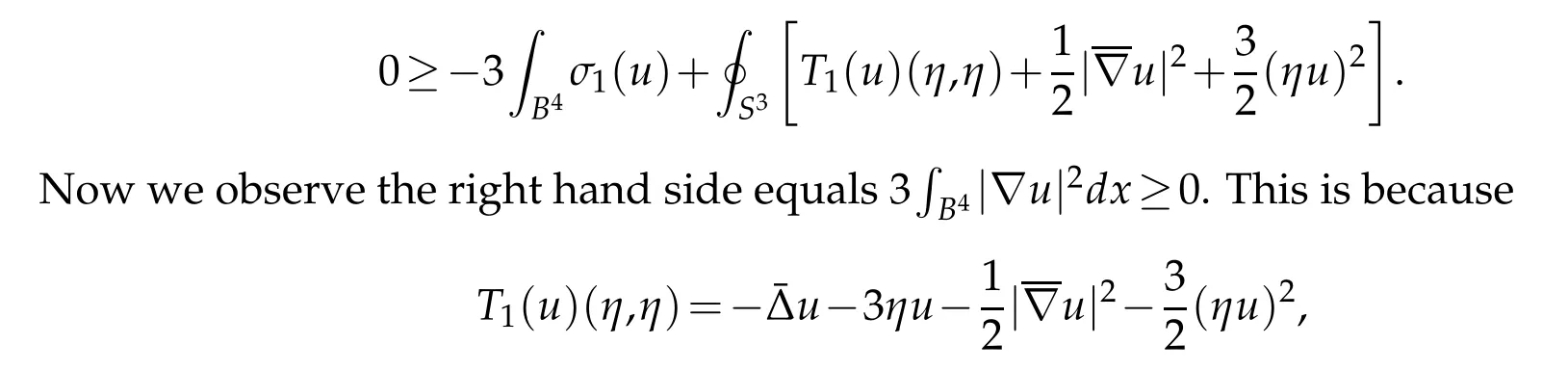
which implies

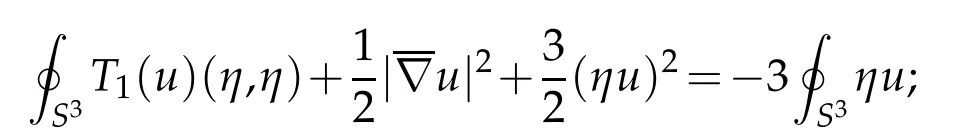
and in the meanwhile,

As a result,

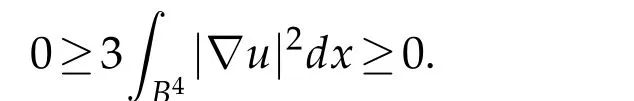
Thus equality holds in both steps.We conclude that u is constant,as desired.

Acknowledgments

The authors would like to thank Sun-Yung Alice Chang for her helpful comments on this work.They are also grateful to the referees for their valuable suggestions and comments.JSC was partially supported by a grant from the Simons Foundation(Grant No.524601).YW was partially supported by NSF CAREER Award DMS-1845033.