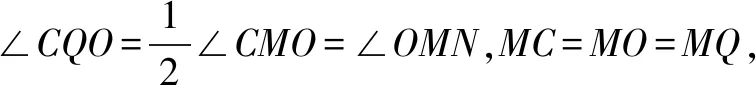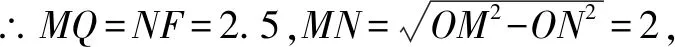巧构辅助圆 妙解几何问题
郑惠容
(福建省泉州市石狮市华侨中学 362700)
圆的有关知识是每年中考必考的内容之一.纵观近几年福建省的中考或质检的数学试题会发现,最后的两道压轴题中有时没有明显的圆的身影存在.但如果我们认真审题,就会发现,其实根据题目中的条件,我们可以自己构造一个辅助圆.那么怎样构造辅助圆呢?笔者结合实例,谈谈构造辅助圆的基本做法.
一、立足基础,利用圆的定义构造辅助圆
根据圆的定义:到一个定点的距离等于定值的点在同一个圆上.这是利用圆的定义添辅助圆的最基本方法.
例1(2016-2017学年福州市期末试题)如图1,C为线段AB上一点,分别以AC,BC为边在AB的同侧作等边三角形△HAC与等边△DCB,连接DH.
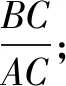
(2)在(1)的条件下,作点C关于直线DH的对称点E,连接AE,BE,求证:CE平分∠AEB;
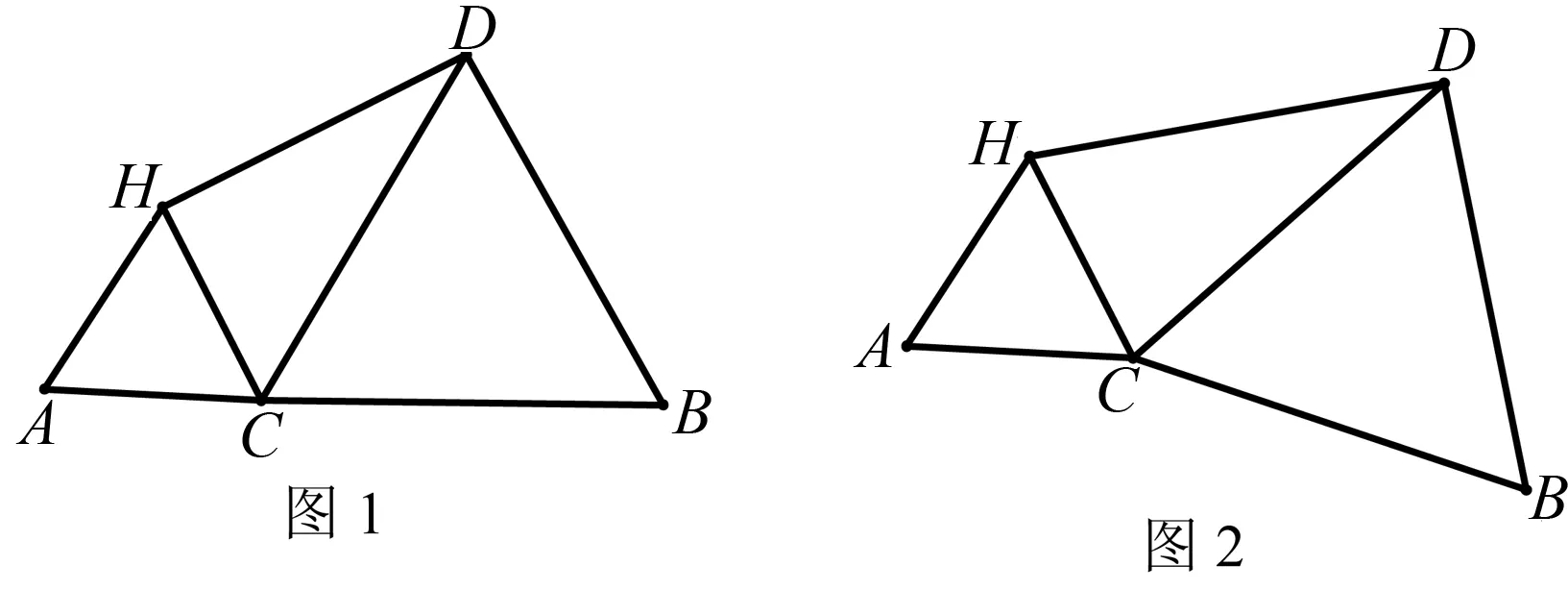
(3)现将图1中△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,C关于直线DH的对称点为E,则(2)中的结论是否成立并证明.
分析(3)根据对称性可知:HE=HC,又因为AH=HC,从而有HC=HA=HE,即A、C、E三点共圆.同理可知B、C、E三点也共圆.
证明(1)(2)略.
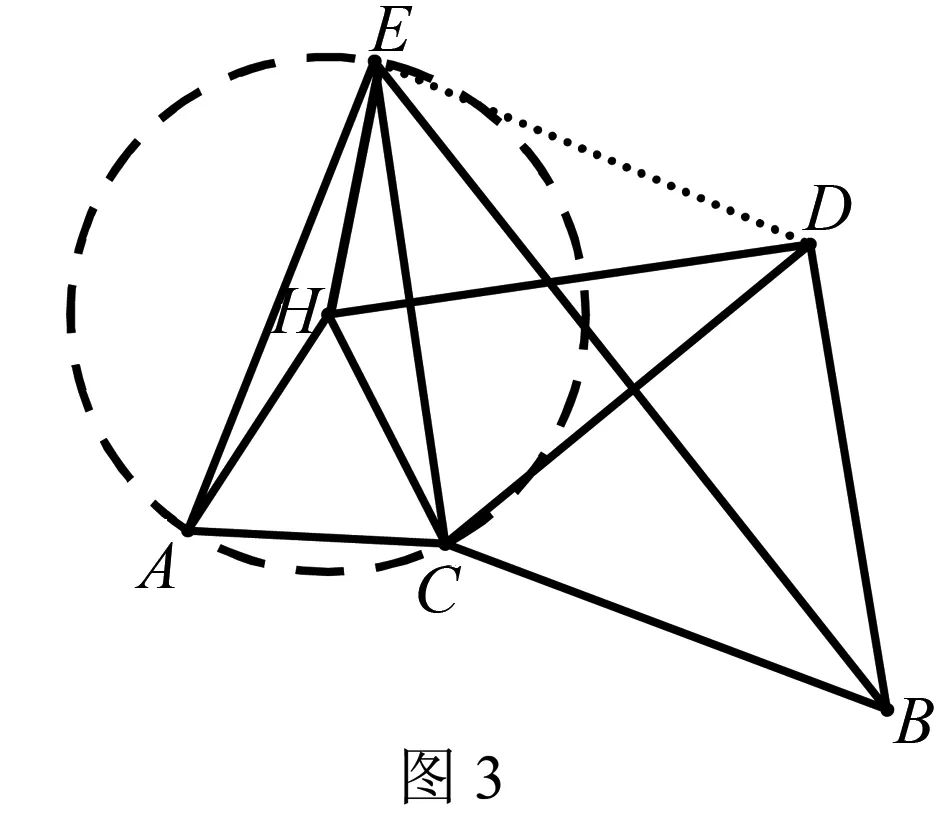
(3)结论仍正确.理由如下:
如图3,由对称性可知:HC=HE.
又∵HA=HC,∴HC=HA=HE,
∴A、C、E三点都在以点H为圆心,HA为半径的圆上.
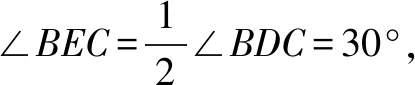
∴∠AEC=∠BEC,∴EC平分∠AEB.
本题解题的关键在于能够根据圆的定义,发现A、C、E三点在以点H为圆心的圆上,同样B、C、E三点在以点D为圆心的圆上,这样做出辅助圆后,就可利用圆周角定理解决问题了.
二、能力导向,利用90°的圆周角所对的弦是直径得到辅助圆
如果题目中出现三角形有一内角为90°,有时可以利用90°的圆周角所对的弦是直径得到辅助圆,然后把问题转化为圆中的问题,利用与圆有关知识来解决相关的问题,这体现了能力导向下培养学生数学思维.
例2(2013年福建省泉州市质检试题)如图4,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿射线CA以每秒2cm的速度运动,同时点Q从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
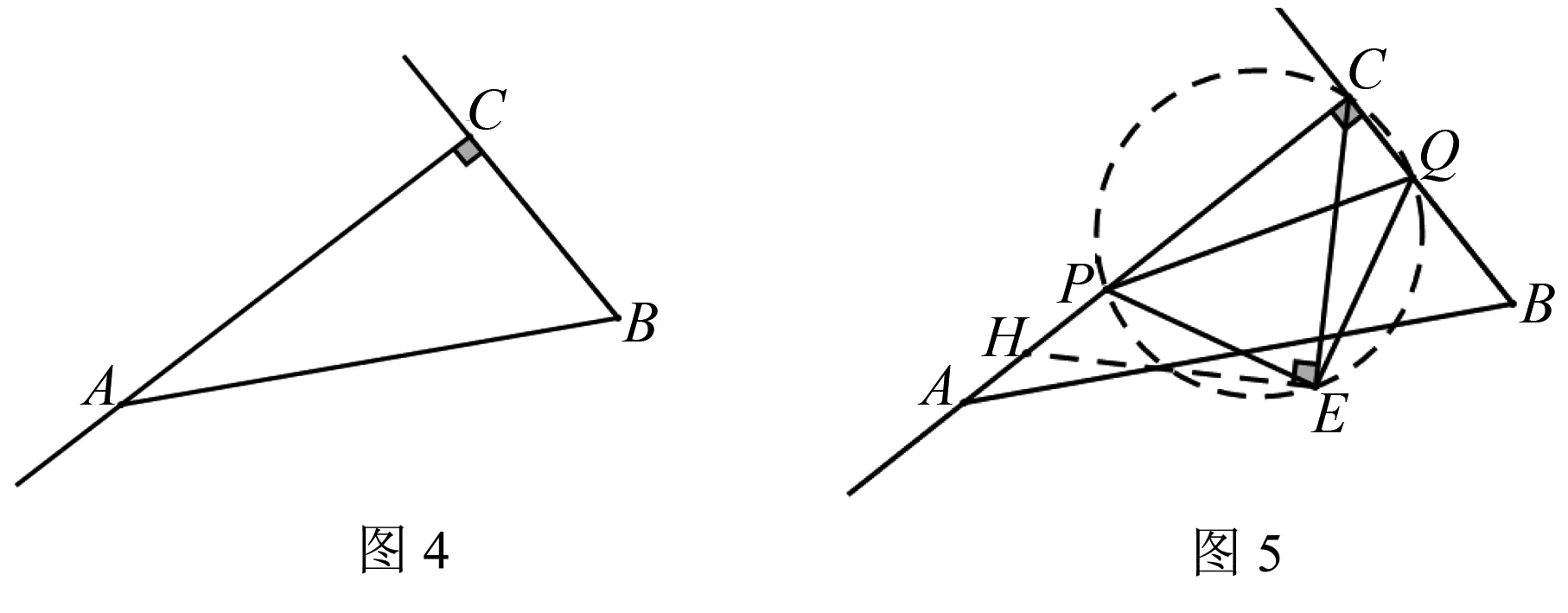
(1)(2)略.
(3)若∠ACB的平分线CE交△PCQ的外接圆于点E.试探求:在整个运动过程中,PC、QC、EC三者存在的数量关系式,并说明理由.
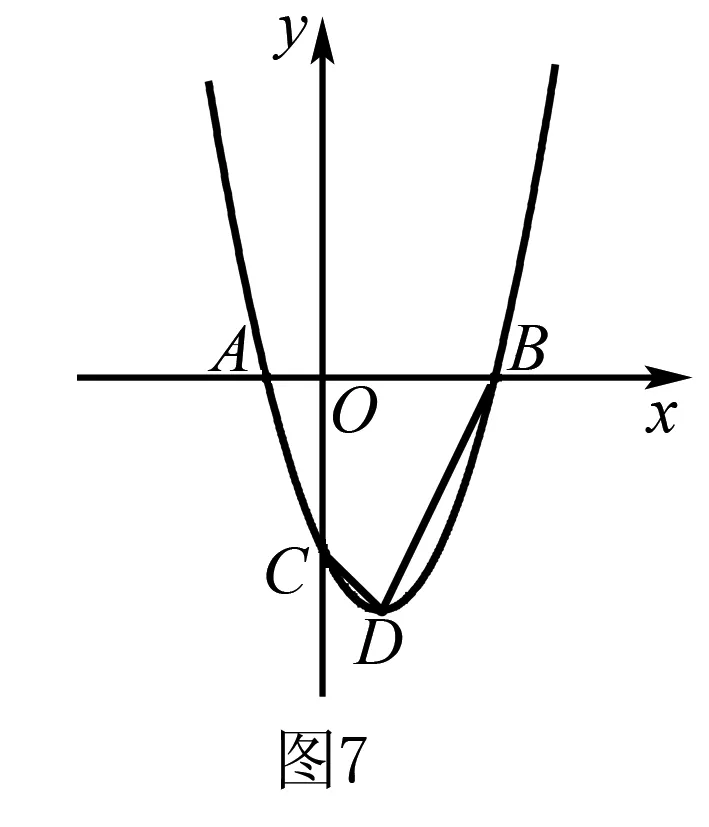
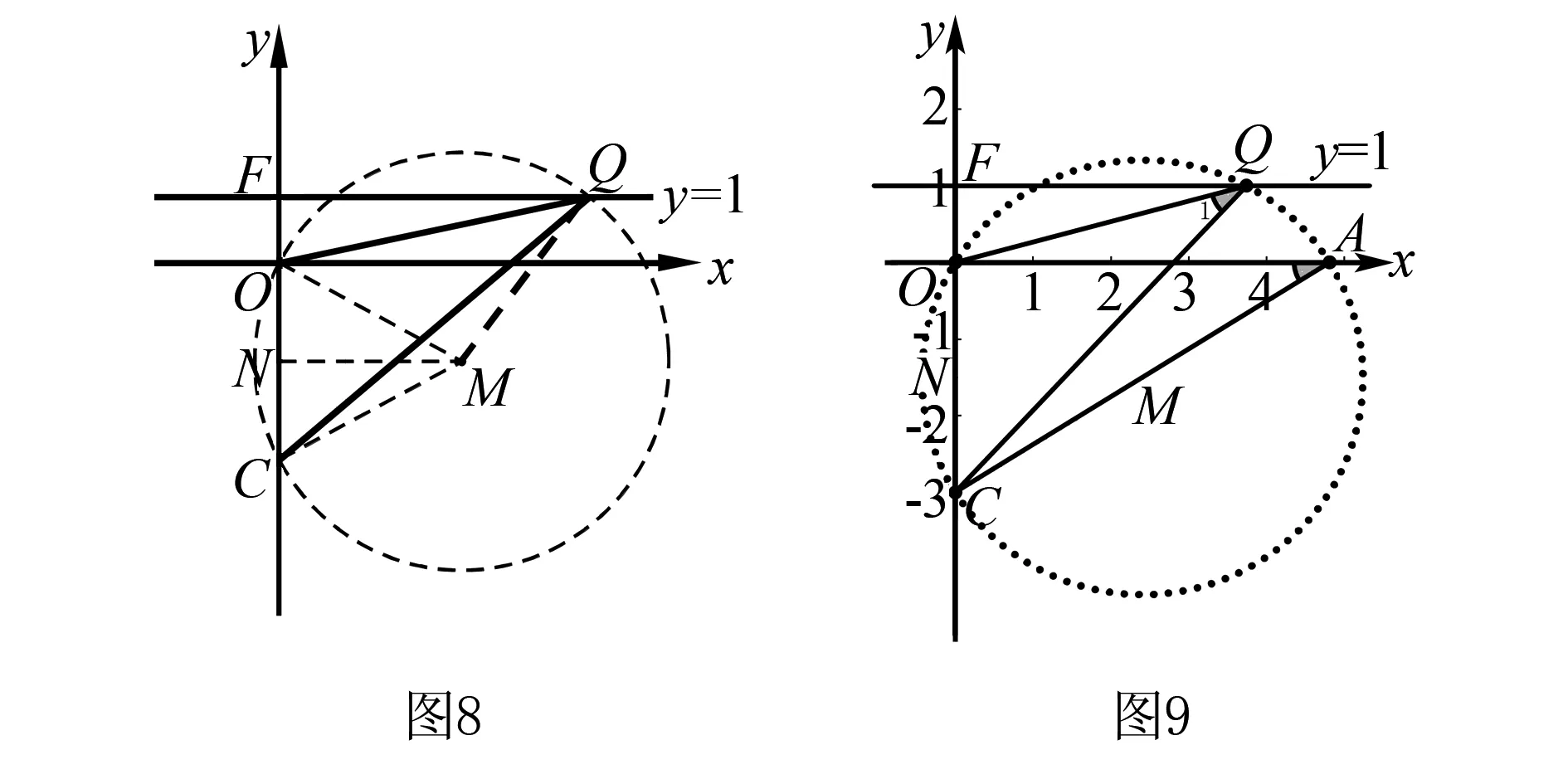
解(3)当0 ∵∠ACB=90°,∴PQ是△CPQ外接圆的直径, ∴∠QEP=90°即∠QEC+∠PEC=90°. 又∵CE平分∠ACB且∠ACB=90°, ∴∠QCE=∠PHE=45°, ∴△QCE≌△PHE(AAS),∴QC=PH. 在Rt△HEC中,EC2+EH2=HC2,EC=EH, 本题中,题目中并没有给出圆,这时要根据题目中给出的条件,画出△CPQ的外接圆,这样才能结合圆的有关性质、全等三角形和勾股定理来解决问题. 我们知道,不在同一直线的三点确定一个圆,有时可以利用这个基本事实来作辅助圆,特别是当三角形的一边为定值,而第三个顶点是一个动点时,要求与角有关的问题,可尝试作出辅助圆,看是否可以把问题转化为圆的有关计算.这需要更高层次的思维,因此,要关注学生差异,抚平台阶,让不同学习水平的学生得到不同程度的发展. 例3(2015年福建省泉州市质检试题)如图7,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点. (1)求b的值. (2)连结BD、CD,动点Q的坐标为(m,1). ①当四边形BQCD是平行四边形时,求m的值; ②连结OQ、CQ,当∠CQO最大时,求出点Q的坐标. 分析我们发现(2)中②问题中的△CQO的边OC是个定值,所以可大胆地构造出△CQO的外接圆⊙M,从而把∠CQO转化为圆心角∠CMO的一半来求. 解(1)(2)①略. ∴sin∠CQO的值随着OM的增大而减小. 又∵MO=MQ,∴当MQ取最小值时sin∠CQO最大, 即当MQ⊥直线y=1时,∠CQO最大, 此时⊙M与直线y=1相切. ∴Q1(2,1). 根据对称性,另一点Q2(-2,1)也符合题意. 综上所述,Q1(2,1),Q2(-2,1). 我们也可以设⊙M与x轴交于点A(如图9),这样就可以直接利用同弧所对的圆周角相等,把∠CQO转化为Rt△OAC中的∠OAC来解决. 本题的成功之处在于构造了过O、C、Q三点的⊙M,从而利用圆周角与圆心角之间的关系或同弧所对的圆周角相等、垂径定理、锐角三角函数的定义以及直线与圆的位置关系来解决问题. 从上面的几个例子我们可以发现,有些问题看似与圆无关,但根据问题的题设、结论或是图形提供的某些与圆的性质相关的信息,可以构造出辅助圆,然后就可以利用圆的相关性质来解决问题.事实告诉我们,只要能掌握好构造圆的基本方法构造出辅助圆,很多看似很难的几何问题就可以迎刃而解.辅助圆,是解决相关几何问题的“金钥匙”.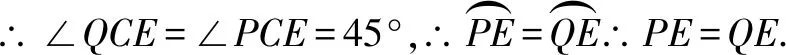
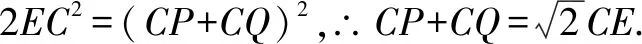
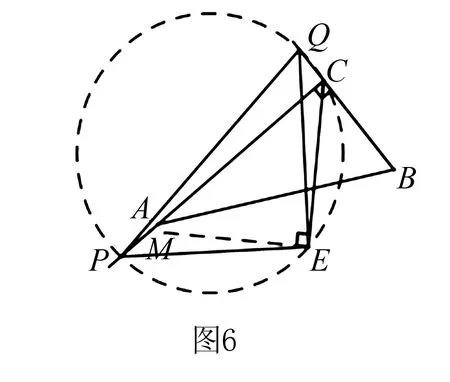

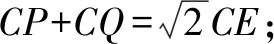
三、关注差异,作三角形的外接圆