基于振动法的岩体纵波波速测试

张一林 刘俊伟 张玉洁

(烟台大学土木工程学院，山东 烟台 264005)

0 引言

岩体指的是在一定空间范围内，包含各种软弱结构面的岩石组成的具有不连续性、非均质性、各向异性的地质体。通过对岩体进行地质勘探和岩体力学测试，可以根据结果的好坏将岩体区分为若干等级，同时对岩体的质量进行评价，从而为工程设计和施工提供具体的参数。岩土体波速测试技术现已广泛的用于工程地质勘察、环境与灾害地质调查、工程质量检测等方面[1]。

在《工程地质手册》(第5版)[2]中进行岩体纵波波速测试的方法主要分为地震波勘察法和超声波探测法，地震波法通过人工激发的弹性波在岩土体中的传播，来判定岩性和地质构造等；超声波法利用超声波在岩土体中的传播特性，解决工程中存在的一系列地质问题。地震法测试指标能代表一定空间范围内岩体的平均动弹性性能，故地震法测试的指标相对于超声波法更有实际意义[3]。赵秀菊等研究了声波速度与岩石硬度的相关关系、地面声波波速与井下测井声波速度相关关系，给出了获取的定性定量结论[4]，侯建国总结了超声技术应用在石材检测中的经验，讨论了石材质量与超声波的波速、振幅的关系[5]。

由于岩体中结构面分布复杂且造岩矿物组成成分不同，地震波的传播路径会受到一定程度的影响。本文针对此问题，提出了一种基于振动法的岩体纵波波速测试方法，并结合理论基础对位于烟台市牟平区养马岛兴运海洋牧场的试验场地进行了工程实测，并与ABAQUS数值模拟结果进行了比较，验证了本文方法的准确性。

1 试验原理

在弹性力学中，以Vp表示岩体中纵波的传播速度，则它们与岩体介质的弹性模量、剪切模量、泊松比之间有如下关系：

(1)

其中，E为岩体的弹性模量,MPa；G为岩体的剪切模量,MPa;ρ为岩体的质量密度,kg/m3;μ为泊松比。

目前工程上主要是根据单孔“一发双收”原理来利用超声波进行岩体纵波波速测试，测试装置由一个发射换能器和两个接收换能器组成[6]。超声波法的测试工艺要求较高，被检测的表面要有一定的光洁度，在室外试验时需要利用耦合剂保证换能器和孔内岩体之间充分的声耦合，否则会产生杂乱的反射波而干扰试验。

地震波法在钻孔附近采用人工振源激发地震波，在孔内不同深度布置三分量检波器接收纵波信号，利用传播时间和路程之比计算岩体的纵波波速。地震波法的试验原理和测试工艺较简单，但地震波在地下节理传播的过程中，岩体节理、裂隙等会影响波的传播规律，导致波的幅值衰减、高频滤波、信号延迟以及波传播速度的减慢，阻碍地震波的传播，加剧波的能量衰减[7]，并且由于波在节理裂隙中的反射和折射现象，并不能确定岩体中地震波的传播路径为直线，因此对后续的数据处理的精度影响较大。

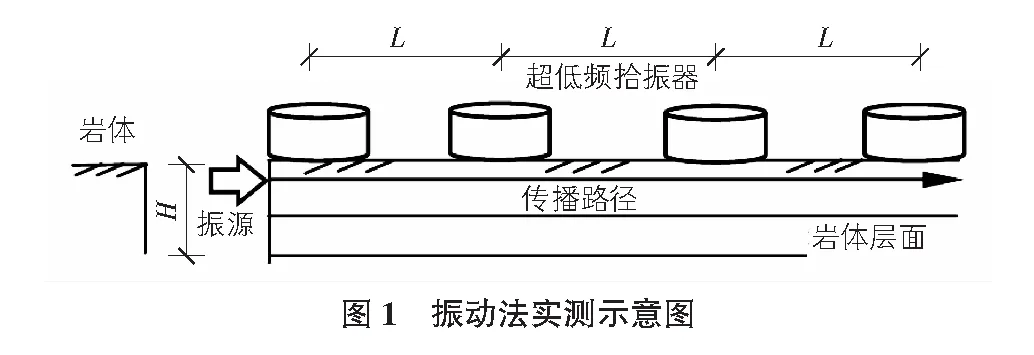
针对上述问题，本文提出了一种基于振动法的岩体纵波波速测试方法并进行了工程实测和ABAQUS数值模拟对比，地震波的频率一般为n×10 Hz～n×102Hz，而超声波的频率一般为n×103Hz～n×106Hz[8]。本文通过锤击激振产生振动波，振动波的主频较低，一般分布在20 Hz左右。钻孔勘察后在近地表的孔壁上激发振动波信号，通过耦合在岩体表面的多个超低频传感器接收信号，采用MATLAB编写互相关程序精确计算出波至时刻后计算纵波波速，本文方法可将纵波的传播路径近似看作水平向的直线进行计算，同时采用了超低频传感器以防止岩体的高频滤波作用，提高了试验精度，振动法测试示意图如图1所示。

互相关函数表示两个时间序列x(n)和y(n)在不同时刻取值之间的相关程度，x(n)和y(n)的相关系数定义如式(2)～式(5)所示：

(2)

ρxy的大小由rxy确定，

(3)

相关函数的定义：

(4)

(5)

当相关系数等于0时，则称x(n)和y(n)不相关；当相关系数越大时，相关性则越强。系统的时间滞后直接由输入输出互相关图中峰值时间的偏移来确定，因此峰值出现的点就是两个函数的偏移量。函数的偏移量即为两个拾振器接收到的同一组测试中同一波形的时间差，根据时差和拾振器之间的距离即可得到各组各段岩体的纵波波速。

2 工程算例

2.1 振动法试验

本次试验场地位于烟台市牟平区养马岛兴运海洋牧场，场地坐标北纬N37°28′47.79″，东经E121°37′29.98″。场地东侧、北侧临海，边坡高度约4 m～5 m，坡面倾角介于20°～30°之间，坡面岩石为全风化和强风化岩，岩体破碎，局部坡脚较缓处堆积第四系松散残坡积物且因海浪长期冲蚀已形成空洞。场地岩性主要为大理岩，岩体为破碎岩体。

现利用941型拾振器对岩体进行波速测试，为验证试验的准确性共进行六组对比试验。布置好仪器后利用TM-100型耦合剂将拾振器与岩体表面耦合，沿振源激发的纵波传播方向布置4台拾振器，试验中941型拾振器间隔分别为0.5 m,0.8 m,1.0 m,1.2 m,1.7 m,2.0 m，利用直尺量取并记录振源到初始传感器及每个拾振器之间的距离，在近地表的孔壁上激发若干次锤击振源，记录测试信号并完成振动法测试。

若测试仪器及测试方法无误，在同一组试验数据中相同振源的四个拾振器信号波形曲线大致吻合，起跳点有一定延时性，受到岩体内的节理裂隙影响，速度幅值会有明显的下降。现利用Origin软件进行数据分析，验证测试数据的准确性。将各通道记录的电压幅值按公式转换得到速度幅值，公式如式(6)所示：

(6)

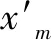
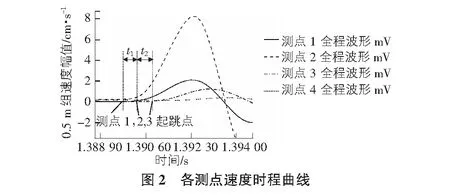
图2为拾振器在间隔0.5 m条件下的水平速度幅值的时程曲线图，t1,t2即为相邻波形之间的时差，通过互相关法计算各波形之间的时差求得波速。对比发现每组的前3台拾振器接受的水平速度幅值时程曲线波形大致相同，末处的拾振器由于距离振源较远，接收的信号变化并不明显，主要原因是因为岩体结构全部或大部遭到破坏，纵波在岩体传播过程中衰减严重，末处的拾振器接收到的信号较弱。

2.2 数值模拟

本文应用ABAQUS建立三维模型，若直接输入振动波会导致波动能量在计算区域内往复反射，且当波传达至人工截断的自由边界时，会在边界发生反射和折射，不符合岩体半无限空间的实际情况[9]。考虑到测试场地岩体为半无限介质模型，因此本文使用黏性边界模拟地震波的传播情况，相对于固定边界而且提高了数值模拟的准确性。

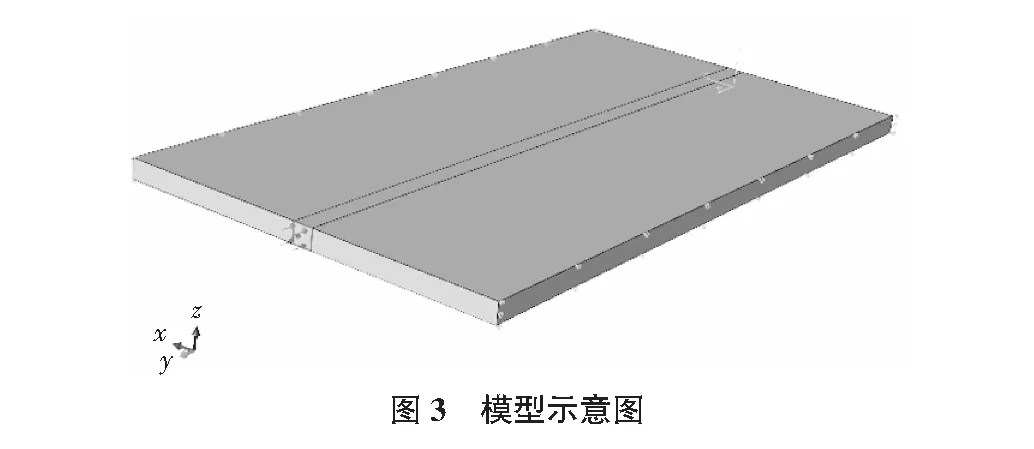
模型介质密度为2 500 kg/m3，杨氏模量E为9.62×109Pa，泊松比μ为0.3，模型大小为15 m×8 m×1 m,模型示意图如图3所示。考虑到岩体的风化，模型中瑞利阻尼的比例系数αR设置为14.75，βR为8×10-5，在模型底部利用Spring/Dashpots单元设置接地阻尼，实现黏性边界的施加，同时在模型一侧1 m×1 m的区域施加幅值力，幅值力的时间与力的大小为半正弦函数关系。为与振动法进行对比，将输出的四个结点的间距分别设置为0.5 m,0.8 m,1.0 m,1.2 m,1.7 m,2.0 m，为使三维模型精确的被单元体描述，采用十结点二次四面体单元划分网格后进行计算。

2.3 结果分析

数据处理结果如表1所示，振动法测试结果平均值为2 150.4 m/s，ABAQUS数值模拟结果平均值为2 256.4 m/s，根据《工程地质手册》(第五版)[2]，推算的测试场地的风化系数约为0.6，考虑到岩体的主要岩性为大理岩及其中的多种矿物成分，判断岩体纵波波速约在1 500 m/s～2 400 m/s的范围内，测试结果在此区间内，且振动法与数值模拟计算误差为-4.70%。

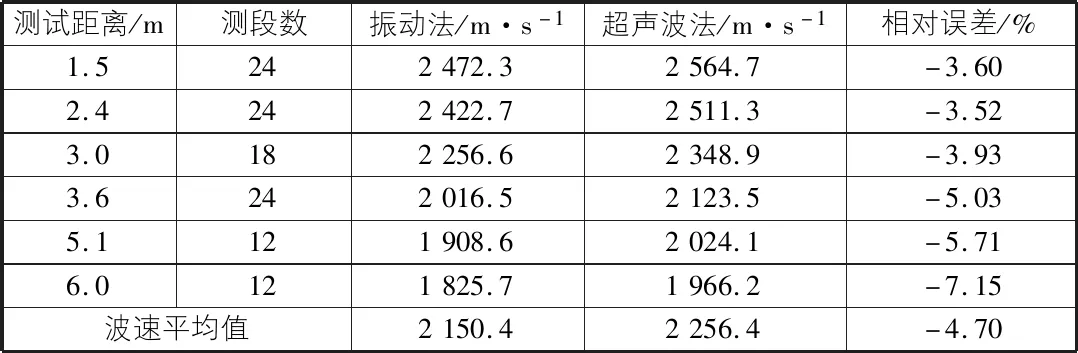
表1 岩体纵波波速测试结果

3 结语

1)本文提出了一种基于振动法的岩体纵波波速测试方法：在近地表的孔壁上激发振动波信号，通过耦合在岩体表面上的多个拾振器接收信号，因此可将波的传播路线看作水平方向的直线进行计算，采用MATLAB程序精确计算出振动波到达观测点的时间t，结合拾振器的位置和距离计算岩体的纵波波速。

2)通过与ABAQUS数值模拟的工程算例精度比较，振动法的测试误差约为-4.70%，在允许范围内，结果表明本文的研究方法可以进行低频的振动测试，解决工程中存在的一系列问题。