二次函数综合题中三角形面积的特殊求法

寇 亮

(甘肃省岷县城郊初级中学 748400)

随着基础教育课程改革的不断深入，人们越来越关注学生数学核心素养的培养.就数学学科而言，数学建模就是数学核心素养的六个方面之一.

求三角形面积的问题是几何问题中常见的问题之一，可用的方法也很多，比如三角形面积公式、割补、等积变形、三角函数等.本文介绍的方法是二次函数问题中实用的一种求面积的方法——铅垂法.

一、知识必备

1.三角形面积公式

2.“割补法”求面积

一些不规则图形或者不便直接计算面积的图形，一般采用“割补法”将其转化为规则图形或可直接计算面积的图形来处理.俗称做“做加法”或“做减法”.

二、方法提炼

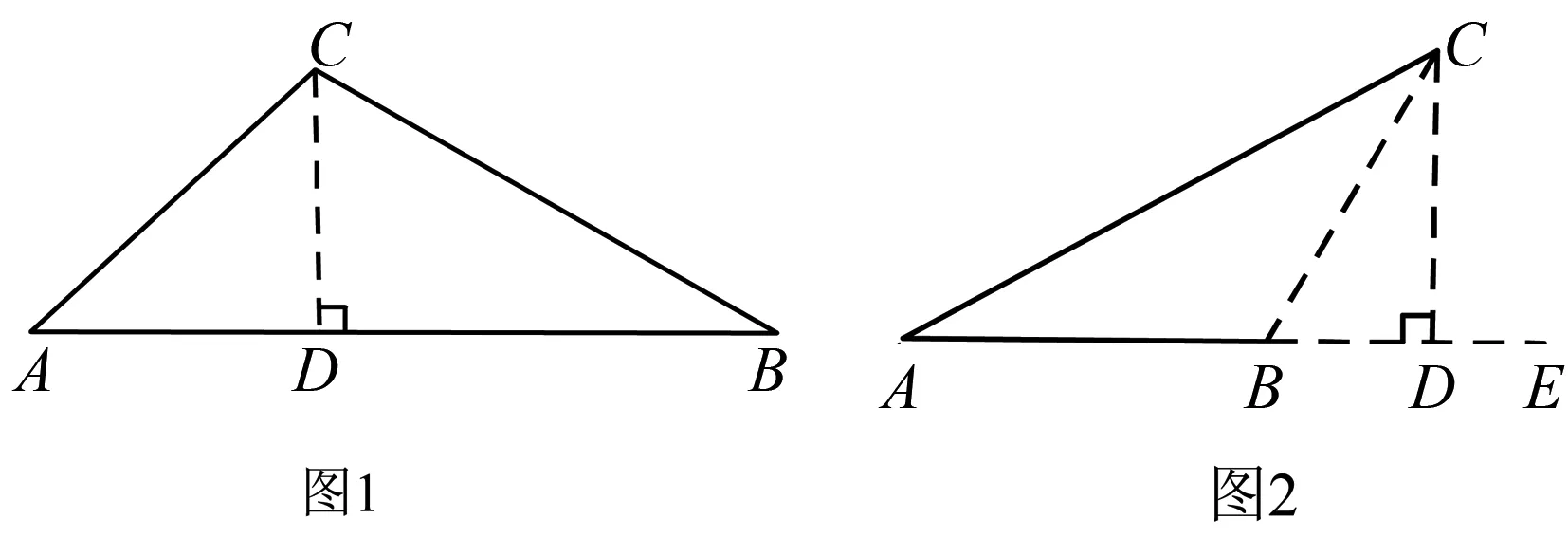
1.基本模型

证明过点C作CD⊥x轴于点D,交AB于点E, 过点A作AF⊥CE于点F,则有

(铅垂法求三角形面积的计算方法在解答题中并不能直接使用，需要加以推导.)

2.模型变式

当点C位于点A的左侧或点B的右侧时，如图4所示，上述计算模型还适用吗？

证明如图5，过点C作AD⊥x轴于点E,交AB的延长线于点D, 则有

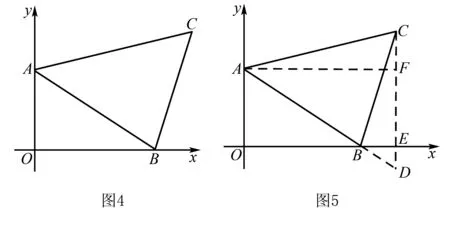
通过上述推理证明，说明无论C与A、B的相对位置如何，这种铅垂法求三角形面积的方法总是适用的，这类题目的构图方法、证明过程、以及最终结论是基本一致的.这一点体现了一些数学题目“万变不离其踪”的特点或者说同学们在学习过程中“以不变应万变”的学习方法.

3.模型升级

铅垂法求三角形面积的方法其实质是割补，重点不在三角形的三个点位置，而是取两个点作水平宽之后，能求出其对应的铅垂高！

(1)如图6，取AB作水平宽，过点C作CD⊥x轴交AB于点D，则CD即对应的铅垂高.

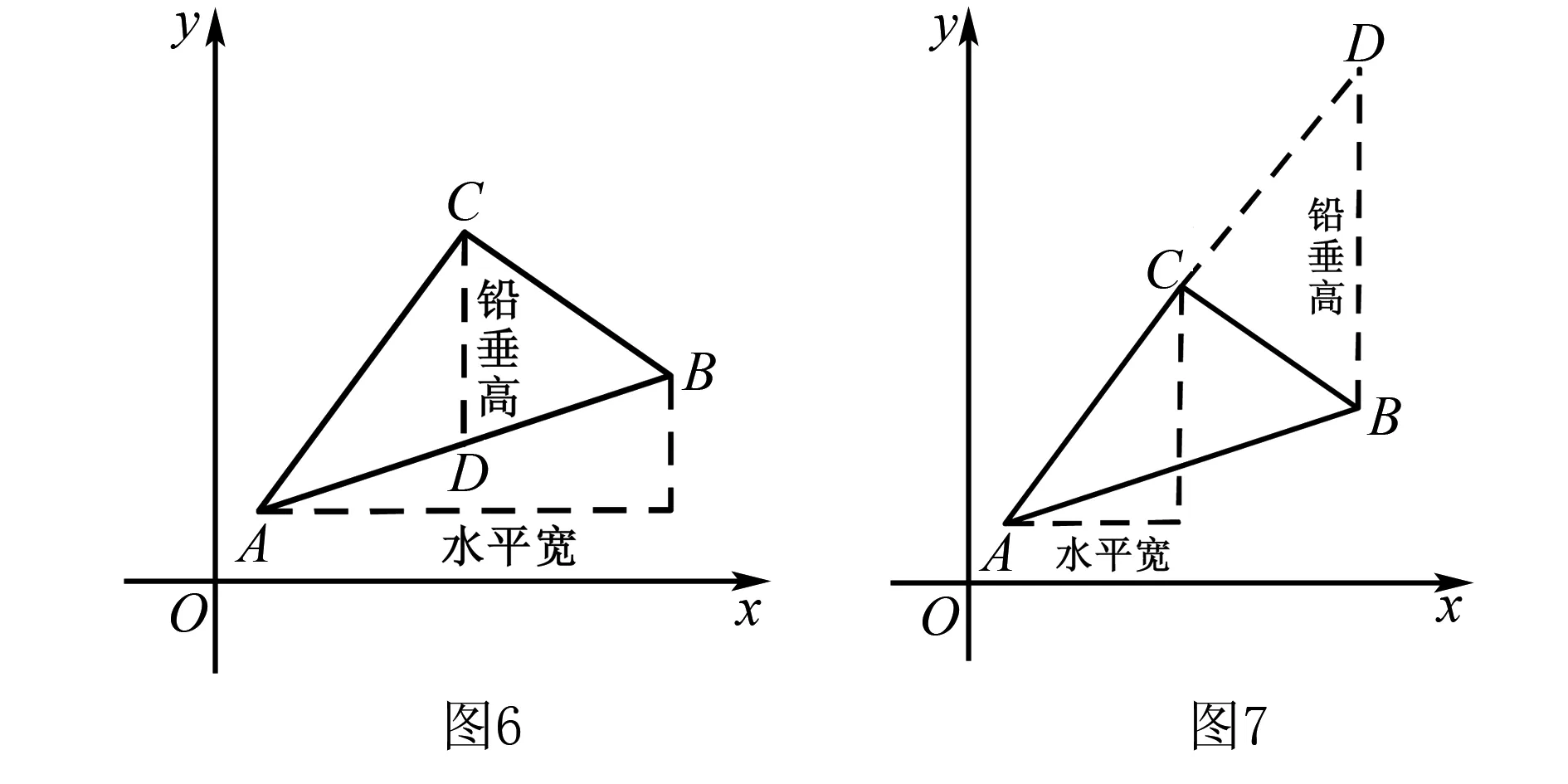
(2)如图7，取AC作水平宽，过点B作BD⊥x轴交AC的延长线于点D，BD即对应的铅垂高.

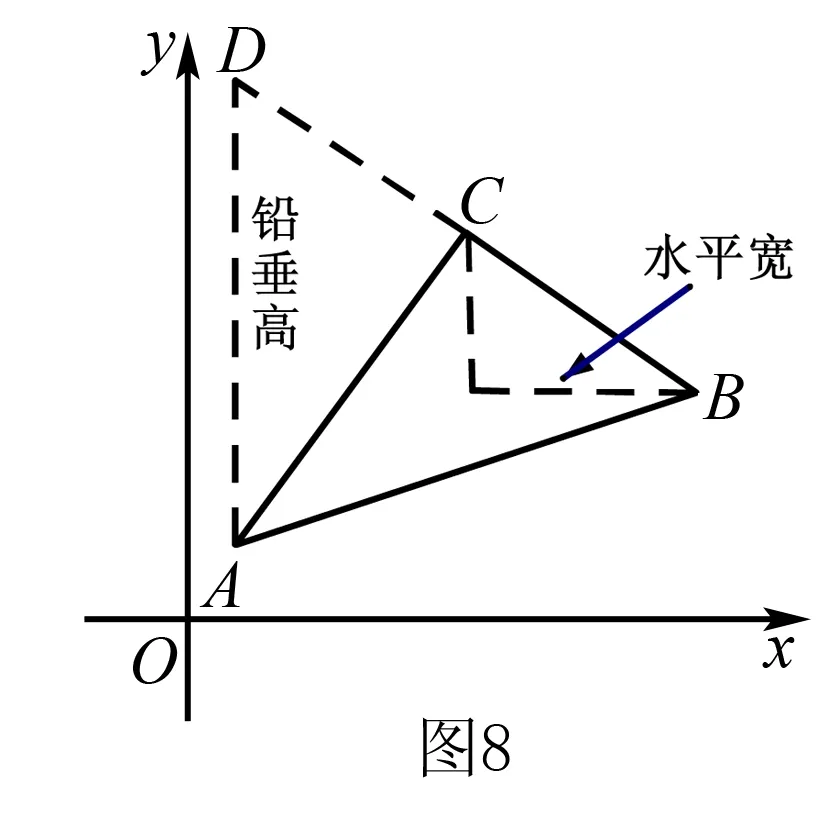
(3)如图8，取BC作水平宽，过点A作铅垂高为AD.甚至，还可以横竖互换，在竖直方向作水平宽，在水平方向作铅垂高.

三、实战演练

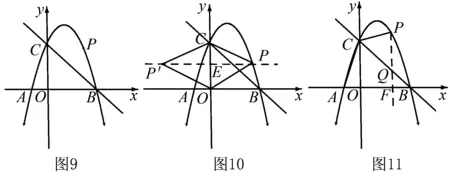
例题(2018年定西)如图9，已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.

(1)求二次函数y=ax2+2x+c的解析式；

(2)连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C，若四边形POP′C为菱形，请求出此时点P的坐标；

(3)当点P运动到什么位置时，四边形ACPB的面积最大？求出此时点P的坐标和四边形ACPB的最大面积.

解(1)将点B和点C的坐标代入函数解析式，得

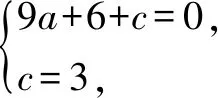
(2)若四边形POP′C为菱形，则点P在线段CO的垂直平分线上，如图10，连接PP′，则PE⊥CO，垂足为E.

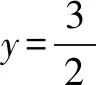
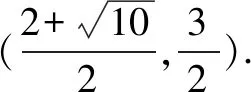
(3)如图11，P在抛物线上，设P(m，-m2+2m+3)，设直线BC的函数解析式为y=kx+b，将B和C的坐标代入解析式,可得

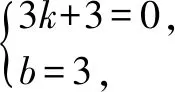
直线BC的函数解析为y=-x+3.

作PF⊥x轴于F，交BC于Q，设点Q的坐标为(m，-m+3)，

PQ=-m2+2m+3-(-m+3)=-m2+3m．

当y=0时，-x2+2x+3=0，

解得x1=-1，x2=3，OA=1，AB=3-(-1)=4，

S四边形ABPC=S△ABC+S△PCQ+S△PBQ

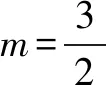
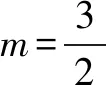
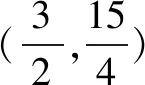
总之，二次函数综合题中用铅垂法求三角形面积的时候，关键是要抓住确定边，最好是沿着动点去做垂线，作完垂线之后再去确定铅垂高和水平宽，这样便于操作.在总结规律的基础上，通过习题加以巩固，才能达到较好的学习效果.