“从三角形内角和到多边形内角和”的探讨

叶巧玲

(广东省惠州市惠阳崇雅实验学校 516213)

一、创设欢乐情境，提出议题

1.猜谜语

(1)形状似座山,稳定性能坚.三竿首尾连,学问不简单.——(谜底：三角形)

(2)四个兄弟一样长,两两相对围成框,阅兵队形常用到,对称轴儿有四条.——(谜底：正方形)

(3)虽说是方块，却长四个角，四角一样大，对面一样长，邻边等不等，不必计长短.——(谜底：长方形)

设计意图：观看视频猜谜语，不但让学生在欢乐中快速进入课堂，还能拉近学生与老师的距离.

2.引出议题

设计意图：复习所学内容,鼓励学生积极回答问题，为新知识的学习营造良好的氛围.

二、课堂推理论证，激活思维

1.探索任意四边形的内角和

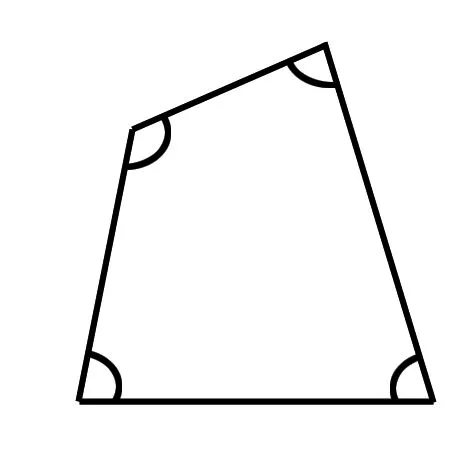
(1)测量法：误差

(2)分割法：严谨

将四边形分割成三角形可有以下三种情况，分别是：

点在内部 点在顶点处 点在边上

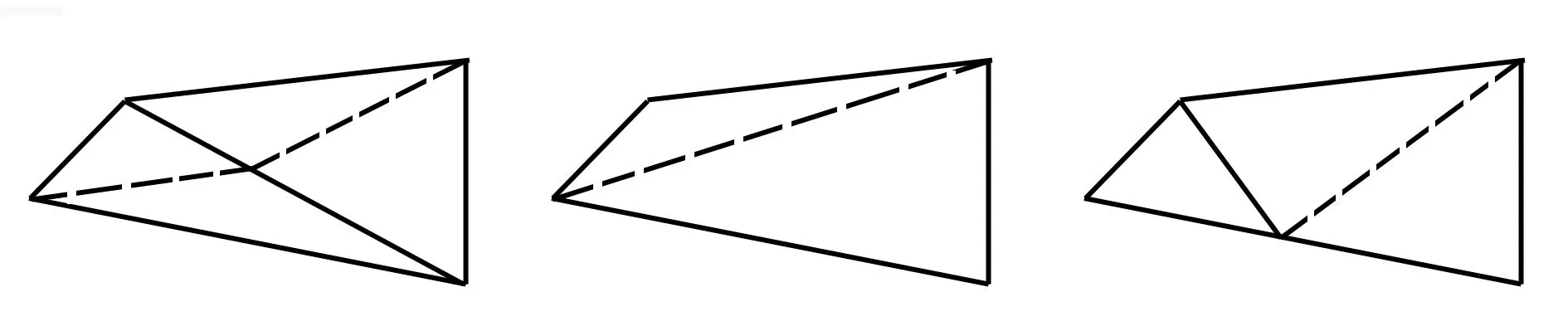
以上三种分割方法都可以将四边形分割成若干个三角形，进而将四边形内角和转化为若干个三角形内角和问题来探索，把未知问题转化成已知，可以借助此方法来探索n边形的内角和.

2.探索多边形内角和，从四、五、六边形入手探究，采用不同分割方法进行， 进而推出n边形内角和.

第一组：在多边形纸片上，连接内部任一点与所有顶点的线段，完成相应表格.

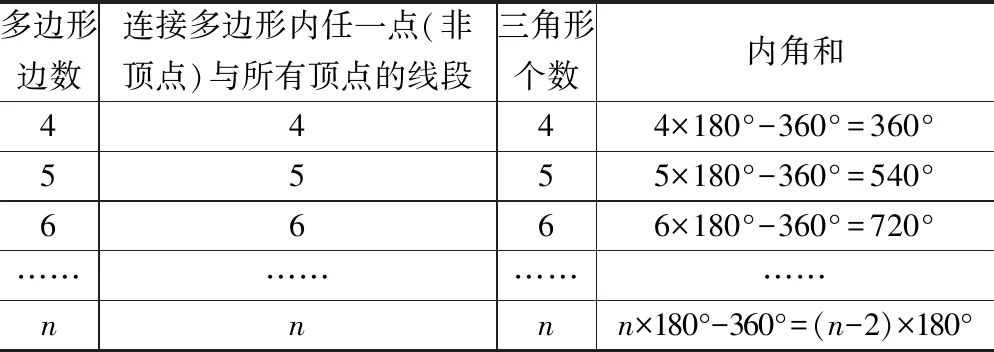
多边形边数连接多边形内任一点(非顶点)与所有顶点的线段三角形个数内角和4444×180°-360°=360°5555×180°-360°=540°6666×180°-360°=720°……………………nnnn×180°-360°=(n-2)×180°

第二组：在多边形纸片上，从一个顶点出发连接所有对角线，完成表格.

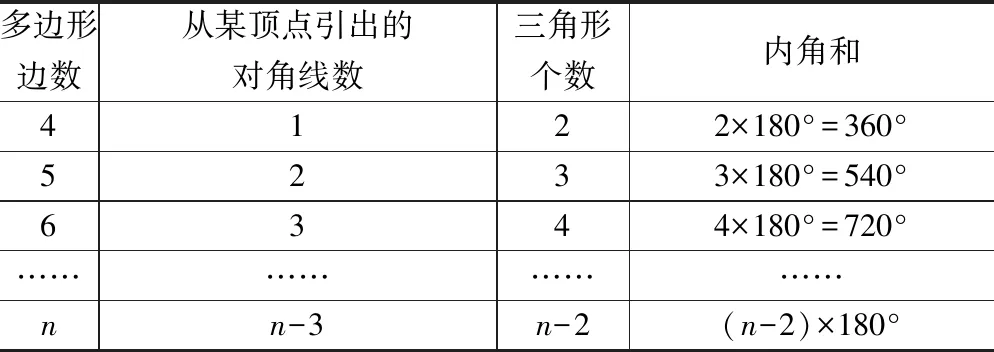
多边形边数从某顶点引出的对角线数三角形个数内角和4122×180°=360°5233×180°=540°6344×180°=720°……………………nn-3n-2(n-2)×180°

第三组：在多边形纸片上，连接某边上任一点(非顶点)与其他顶点，完成表格.

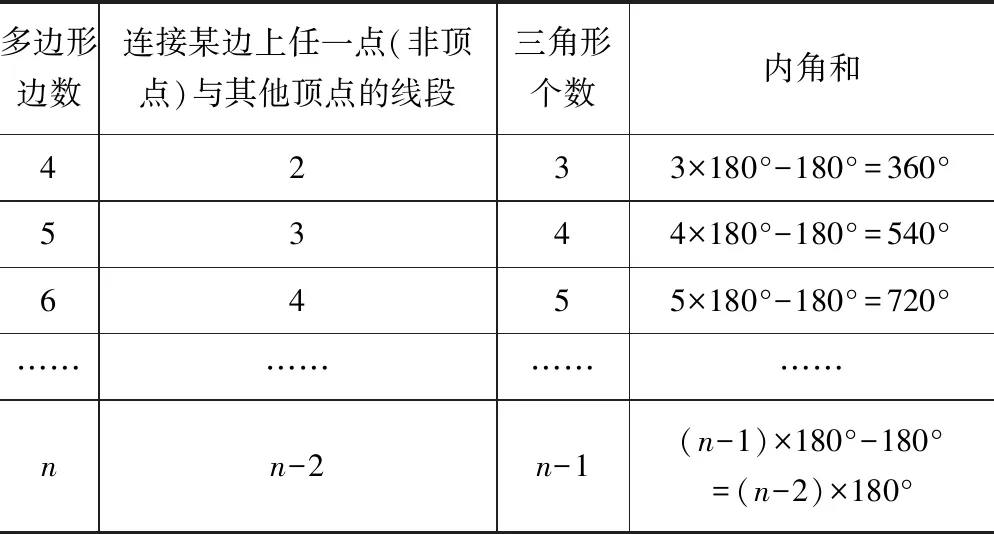
多边形边数连接某边上任一点(非顶点)与其他顶点的线段三角形个数内角和4233×180°-180°=360°5344×180°-180°=540°6455×180°-180°=720°……………………nn-2n-1(n-1)×180°-180°=(n-2)×180°

思考：以上三种情况的点在多边形内部或者边上，能不能在多边形外部取一点探究？

3.小结

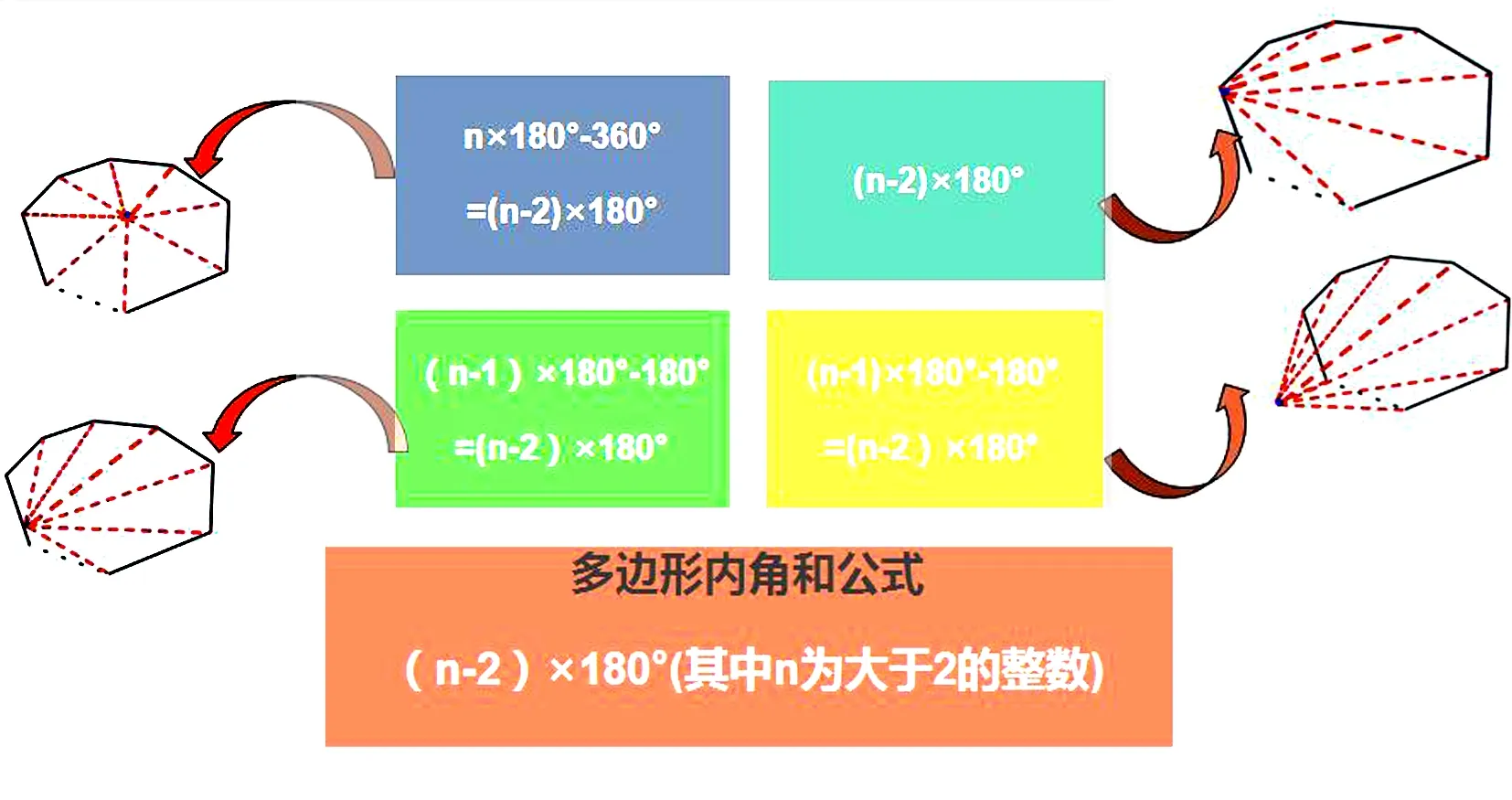
教师点拨：以上方法均可推出多边形内角和公式，其中点在多边形内部应该是学生最容易想到的，对角线的情况则对学生来说最容易记忆，但对角线的条数与分得三角形的个数又很容易混淆.

设计意图：借助辅助线将多边形转化成三角形内角和解决，是把未知转化为已知，从特殊情况到一般情况、从简单问题深入到复杂问题等方法的体验，同时提高学生的表达能力、动手能力及归纳能力.

三、例题深入学习，学以致用

例1

例2已知在四边形ABCD中有一组对角互补.求证：另一组对角互补.

证明如图，∠C+∠A=180°.

∵∠A+∠B+∠C+∠D=(4-2)×180°=360°,

∴∠B+∠D=360°-180°=180°.

即另一组对角互补.

变式训练：在四边形ABCD中，BA⊥AD，CB⊥DC,求∠B与∠1的关系.

解∠B=∠1.理由如下：

∵AD⊥AB，CD⊥CB,

∴ ∠A+∠C=180°.

∵∠A+∠C+∠B+∠ADC=(4-2)×180°=360°,

∴∠ADC+ ∠B=360°-180°=180°.

而∠ADC+∠1=180°，∴ ∠B=∠1.

设计意图：让学生在欢乐探索后，深入学习例题并学以致用，体验应用结论的成就感，同时考查学生对多边形内角和的掌握程度及运用公式的能力.

四、自主针对测评，巩固新知

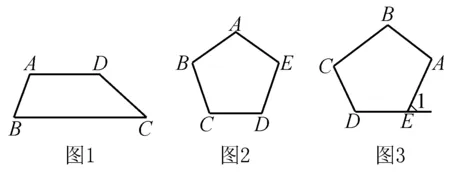
(1)(2017·广州)如图1，四边形ABCD中, ∠A=110 °，∠B=70 °, ∠D=120 °, 则∠C= (60 °).

(2)(2017·湖南) 如图2，多边形ABCDE的每个内角都相等，则每个内角为(108°) ．

(3)(2017·江苏)如图3， 在五边形ABCDE，若∠1=60°，那么∠A+ ∠B+ ∠C+ ∠D=(420°).

设计意图：预测“欢乐课堂”的教学效果，达到巩固新知的目的，与中考紧密联系，让学生有针对性地学习.

五、自主高效归纳，升华新知

知识回顾:1.从n边形的一个顶点出发，作出(n-3)条对角线，所分成的三角形个数是(n-2)个.

2.多边形内角和公式：(n-2)×180°.

设计意图：回顾本节课的重点，体会本节课的数学思想.

六、趣味作业布置，课后反馈

1.复习本课知识、回顾探索问题的思路与方法.

2.趣味思考： 2019年国庆来临之际，小晴想设计一个内角和是2019°的多边形图案,她能实现吗？

设计意图：引导学生回顾知识点，最后以一个有趣的数学问题引导学生思考并灵活运用本节课知识点.

七、课后总结经验，查漏补缺

以“欢乐课程”为线索，注重培养学生的口头表达能力、逻辑思维能力、动手能力等，采用师评、互评、自评三种方法对教学效果进行评价.

设计意图：为提高学生的表达能力、归纳能力等，鼓励学生畅所欲言，形成个人的知识框架.