巧设“问题串”增强课堂有效性——初中数学备考复习例谈

吴流坤 董 莉

(云南省玉溪市易门县教育科学研究所 651100)

“问题串”是指在一定的学习范围内或主题内，统一目标，按照一定逻辑结构精心设计的一组问题.使用“问题串”进行教学，实质上是引导学生带着问题(任务)进行积极的自主学习，由表及里，由浅入深地自我建构知识的过程.“问题串”教学设计的基本思路是：首先教师提出问题，然后学生带着问题阅读教材、独立思考、归纳的出自己的答案，最后师生共同总结，教师做出归纳、简评.“问题串”教学设计的最大优点在于学生在思考的过程中得出答案，经历了思考的过程.

美国心理学家布鲁纳指出，“教学过程是一种提出问题和解决问题的持续不断的活动，思维永远是从问题开始的”.特别在“问题串”的驱动下，学生的思维逻辑、学习激情、创新能力等方面均得到提高与增强.而初中生思维活跃，好奇心较强，因此，在教学中应改变传统教学方式，利用“问题串”优化习题教学模式，提升教学效果，培养学生的探究能力，具有重要的意义.

针对不同的教学内容如何设计有效的“问题串”，提高教学效果呢？下面结合自己深入一线课堂调研复习课时听到的案例谈几点思考.

一、设计整合型“问题串”，综合运用，提升学生运用能力

数学是一个整体，其不同的分支之间存在着实质性联系.为了使学生头脑中的知识点串成线、由线成面，全面系统地分析并解决问题，教师必不可少把零散问题进行有机整合.整合型“问题串”主要在知识的结合点处设计，注重知识间的内外、横纵联系.

例1一元二次方程复习

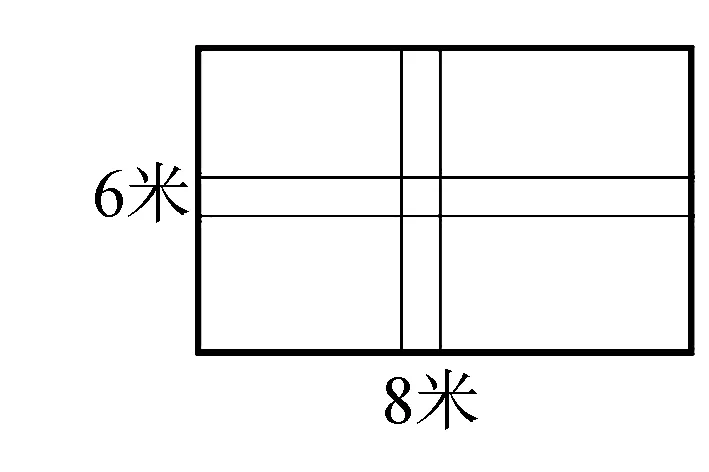
如图，在长为8米，宽为6米的矩形花园里修建两条宽度相等且互相垂直的道路，剩余部分进行绿化种植，要使绿化面积为24平方米.

问题1.道路的宽应为多少米？怎么求?

问题2.x2-14x+24=0这是什么方程？

问题3.x2-14x+24=0这个方程有解吗？有几个解？你是怎么判断的？

问题4.如果方程变成这样x2-14x+m=0，且方程有两个实数根,则m的取值范围是____；

问题5.再变成mx2-14x+24=0，且方程有两个实数根，则m的取值范围是____.

问题6.怎么解这个方程x2-14x+24=0？你还可以用哪些方法来解？

以上“问题串”从“点”出发，把“面”带出来呈现给学生，渗透数学方法、开拓学生思维，引导学生从不同的层次、角度、方式和起点去思考解决问题，全面提升学生综合运用能力，引导学生形成一个经纬交织、融会贯通的知识网络.

二、设计递进型“问题串”,经历知识的形成，培养学生的归纳能力

学生是数学学习活动的主体，任何外在的信息只有通过学生自己的加工和处理，才能内化成学生的认知，所以在复习教学中应注重学生的探究活动，说一说、想一想、动一动、做一做，让他们经历数学知识的形成过程.

递进型“问题串”的设计可从学生熟悉的情景入手，设计一串由近及远或简单到复杂或特殊到一般或具体到抽象的“问题串”，设计难度适中、排列有序、循序渐进，形成有层次的开放性系统，低起点、高落点，一步一步引导学生深入思考，使学生真正经历知识的发生和发展过程，更好地把握其内涵与外延，体验探究的过程，提高归纳能力.

复习二次函数时，学生对知识的梳理、学习方法的归纳能力直接影响学习效果.

例2二次函数y=x2-2x-3

问题1.它的图象是一条____.

问题2.开口向____.

问题3.对称轴是____.

问题4.顶点坐标是____.

问题5.抛物线与x轴的交点坐标是____.

问题6.抛物线与y轴的交点坐标是____.

问题7.化为顶点式为____.

问题8.化为两点式(交点式)为____.

问题9.用五点定位法画出函数的大致图象.

问题10.观察图象，当x____时，y随x的增大而增大;当x____时，y随x的增大而减小.

问题11.当x=____时，函数值y有最____值，这个最值是____.

问题12.观察图象，方程x2-2x-3=0的解是____.

问题13.当x取____时，函数值y>0；当x取____时，函数值y<0.

问题14.抛物线y=x2-2x-3可以由抛物线y=x2先向____平移____个单位，再向____平移____个单位而得到.

问题15.如图，S△ABM=____,S△ABC=____.

问题16.在抛物线y=x2-2x-3上是否存在点P，使得S△ABP=6?如果存在，求出P点坐标；如果不存在，请说明理由.

问题17.另有一条抛物线与抛物线y=x2-2x-3关于x轴对称，求这条抛物线的解析式.

以上由易到难的阶梯式呈现的“问题串”，面向了全体,适合不同层次的学生，有助于引导学生深层次地联想、比较、分析，有利于低层次的学生向更高的目标迈进，把复杂的二次函数零散的知识点串联起来，达到纵向深入，串点成线的目的，并减少了不必要的重复，以问题组带出知识点,以问题组带方法，引导学生以自主探索、合作交流的方式学习，整个学习过程放手给学生，把教师教翻转到了学生的学上来，让学生在解决“问题串”的过程中感受数学、体验数学和理解数学，发展解决问题的策略，树立正确的数学观.

三、设计变式型“问题串”，延伸拓展，培养学生发散思维能力

为了使学生对数学知识有更深层次的理解与运用，教师应向学生展示知识的不同面，引导学生多角度、多方位审视问题，认识问题的本质从而促进学生的发散思维和求异思维的发展.变式型“问题串”主要以教科书中例题、习题为对象，在保持原题本质的基础上进行延伸拓展，通常变换条件或结论或因果关系倒置，通过变式型问题串的训练，学生对某一孤立、零散的问题形成有规律可循的一系列问题，对所学知识举一反三、触类旁通，从而提高复习课堂教学的有效性.

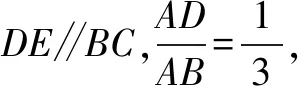
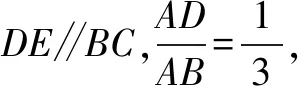
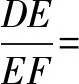
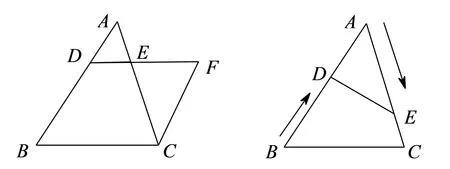
[变式问题3]如图，在△ABC中，AB=15cm，AC=10cm，点E从点A开始沿AC边向C点以1cm/s的速度移动，点D从点B开始沿BA边向点A以1cm/s的速度移动，如果点E、D分别从A、B同时出发(当E点到达C点时，D点同时停止)，问经过几秒钟后，△ADE与△ABC相似？

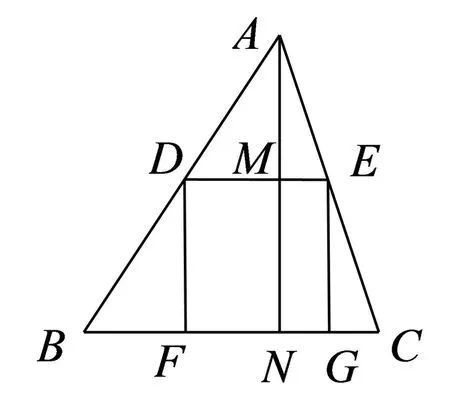
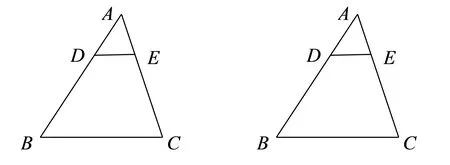
[变式问题4]△ABC是一块锐角三角形材料，D、E分别是AB、AC上的点，若DE∥BC，点F、G在边BC上，且BC=12cm，高AN=8cm，如果把四边形DFGE加工成正方形零件，这个正方形零件的边长是多少cm？

这些“问题串”涉及相似典型模型的应用，如，“A型”“X(8字)型”等，有利于巩固相似三角形的判定和性质，起到举一反三的作用，通过一个题的变式练习，渗透了模型思想、数形结合思想、方程思想等数学思想，随着问题的不断变换，不断解决，学生的思维能力得到了提高，有效地增强了学生思维的敏捷性和应变性，培养了学生思维的深刻性，从而提高复习效率.

四、设计适合学生认知特点的探索型“问题串”,发现规律，培养学生的探索能力

从数学的发展看，数学本身也是充满了观察与猜想的探索活动.探索型“问题串”能较好地帮助教师引领学生去探索和发现数学规律，更主要的是经历从特殊到一般，从一般到特殊这种探索规律、验证规律的过程，了解从特殊到一般，从一般到特殊的数学思想方法.

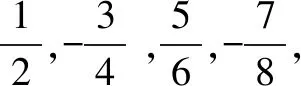
问题1.从分子变化来看你能发现什么规律？

问题2.从分母变化来看你能发现什么规律？

问题3.从各项符号变化来看你能发现什么规律？

解析分子：1，3，5，7，…是从1开始连续的奇数，奇数规律,即：2n-1；

分母：2，4，6，8，…是从2开始连续的偶数，偶数规律,即：2n；

符号：奇数位置为正，偶数位置为负(1，-1,1，-1，…),符号规律(利用-1的奇偶次方来判断)即:(-1)n+1.

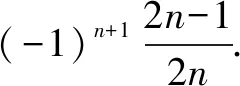
许多数学定理、性质、公式、法则的发现都要经历一个艰苦曲折的思维推理过程.探索型“问题串”的设计就要围绕定理、法则、公式的发生、形成、发展三个过程展开，通过引导学生观察、动手操作、比较分析、猜想归纳，在探究活动中学数学，获得数学学习的体验，提高探索能力，体味到数学的无穷魅力，以此促进学生的数学学习.

题5规律探究：如图，在三角点阵中，从上往下有无数多行，

其中，第一行有1个点，

第二行有2个点,

第三行有3个点,

第n行有n个点

问题1：前1行的点数和是____;

问题2：前2行的点数和是____;

问题3：前3行的点数和是____;

问题4：前4行的点数和是____;

问题5：前5行的点数和是____;

……

问题6：三角点阵中前n行的点数和是____.

前n行的点数和：1+2+3+…+(n-2)+(n-1)+n.

模仿高斯算法：设三角点阵中前n行点数和为S,

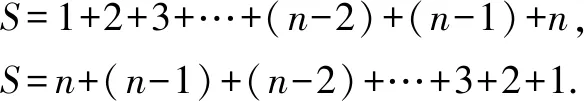
两式相加得：2S=(1+n)+(2+n-1)+(3+n-2)+…+(n-2+3)+(n-1+2)+(n+1),

以上“问题串”,化繁为简，让学生“细心观察-大胆猜想-精心验证-知难而进”，激发学生的学习欲望，从而由点到面的拓展,为学生采用合情推理(归纳与类比)探索未知世界积累了丰富的活动经验.

总之“问题是数学的心脏”，数学知识、思想、方法、观念都是在解决数学问题的过程中形成和发展起来的.所以，“问题串”的设计不仅要考虑教学内容，还要关注学生的心理特点和认知规律，只有精心设计“问题串”，并且“问题串”又在实际教和学中功效被充分的发挥和挖掘，这样才真正有助于学生思维活动的开展，才真正实现课堂的“有效”.