例谈初中数学解题训练教学

宋景华

(河南省安阳市幸福中学 455000)

在很长一段历史时期内，初中数学课程教育的基本任务就是为了提高学生的考试成绩，且多数教师都认为“课堂灌输”与“题海战术”是培养学生数学应试能力的重要措施，导致初中生背负着繁重的考试压力.但是，数学练习贵精不贵多，只要初中生能够从根本上把握某类题型的解题思路与解题策略，辅以必要的专项练习，那么不管数学问题条件、设问方式如何改变，只要这个问题遵循着数学知识的发展规律，那么初中生便能灵活应对，准确解答.因此，初中数学教师应该要充分利用典型的数学例题来组织解题训练，鼓励学生全程参与例题解析与例题变形、应用等学习过程，促使学生形成良好的问题解决能力，减少学生的解题困惑.

一、挖掘教材例题中的数学思想方法

数学思想方法实际上就是反映数学知识规律的抽象思想与解题规律，已经随着数学教育的素质教育发展成为最基本的教学任务.但是，传统的初中数学教师却过于看重理论知识的传授进度，忽视了数学思想方法的归纳与提炼，使得学生的数学知识记忆出现了零散、碎片化问题，限制了初中生解题能力的发展.对此，初中数学教师应该要积极挖掘教材例题所呈现的数学思想方法，显化每一个例题的解题规律，分门别类地归纳有效结论，为学生提供一个解题模板与思路.

就如在“图形的旋转”一课教材中，人教版教材中便有这样一道例题：

△ABC是等边三角形，△ABP顺时针旋转后能与△CBP′重合，请问旋转中心是哪一点？旋转角是几度？连接PP′后，△BPP′是什么图形？

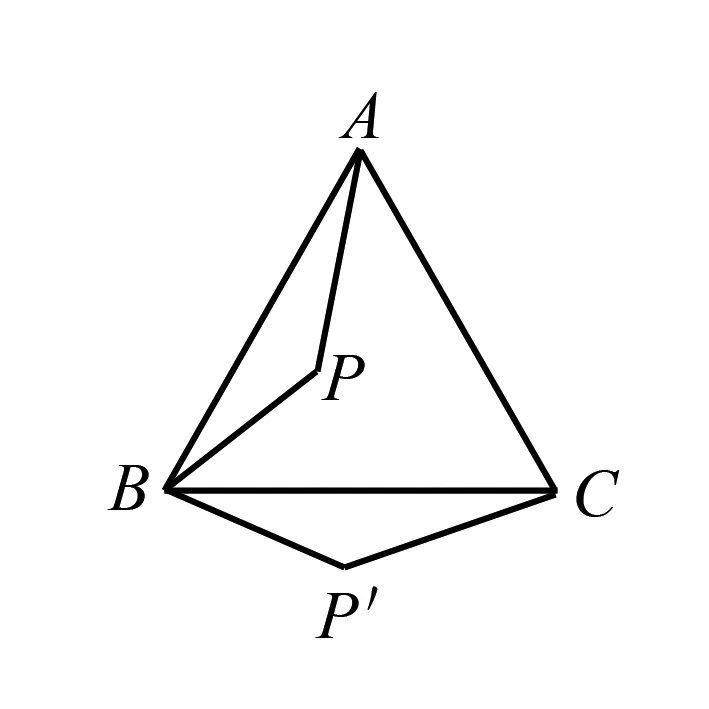
这个问题是“图形的旋转”一课的经典例题，也是最常出现的一种题型.在本例题解题过程中，学生需通过图片信息展开大胆想象，根据具体的几何证明完成解题任务，而这个思想活动便是数形结合思想方法.因此，在例题解析中，我就为学生解释了何为数形结合思想方法，借助这一数学思想突出了“空间与几何”板块常用的一种解题思路，引导学生回顾了自己利用数形结合思想方法的现实回忆.由此，学生便能准确理解数形结合思想方法的一般特征，切实优化自己的解题思维.

二、引导学生汇总例题解题思路之外的解题策略

我们都知道，“问题是数学的心脏”，在初中数学教材中设计例题也是为了降低数学知识的抽象性与逻辑性，使得初中生在例题解题过程中及时掌握相应的解题策略.但是，通常来讲，数学例题并不会汇总所有的解题方法，而是会呈现最为经典、最为重要的解题思路.针对这个特征，初中数学教师应该引导学生探究与归纳教材所演示的解题思路之外的其他解法，使其自主对比与归纳多种解法，以便在后续数学练习中随着题意条件、设问方式等灵活选择相应的解题方法，并进一步提升学生的解题能力.

就如在“一元二次方程”一课的课本例题中，人教版教材以框图形式展示了配方法的解题思路与计算步骤，由此引导学生学习配方法的由来与客观规律，以便切实引导学生掌握解答方程问题的常规思路.但是，除此之外，公因式、因式分解法等都是方程问题的重要解题策略.因此，我就让学生们用公因式、因式分解法、配方法同时解答教材例题，积极对比方程问题多元解法的优缺点，借此提升学生自身的解题能力.同时，方程与函数思想同样也是数学思想方法的重要组成部分，对学生的理性思维能力发展十分重要，也是后续数学学习中的重要学习思路.因此，我也借此强调了方程与函数思想的重要性，引导学生在列方程、解方程活动中强化自己的数学思想方法，促使学生在数学解题过程中提升自己的数学学科素养.

三、借助教材例题组织同类型解题训练

能力的形成必然需要通过大量的练习与实践检验，即便学生透彻理解了教材例题所反映的数学思想方法与解题策略，同样也需要学生在数学练习中积极应用，由此巩固课堂所学，提升自身的数学素养与解题能力.因此，初中数学教师应该要以教材例题作为切入点来设计同类型专项练习，促使初中生在解题训练中提升自身的数学学科素养，完善学生的解题经验.值得一提的是，在组织数学练习时，初中数学教师不可选择“题海战术”，而是要有针对性地设计具体的练习内容与练习数量.

就如在“实际问题与一元二次方程”一课中，人教版数学教材设计了传播问题、增长率问题、几何图形面积问题、匀变速问题四类实例，且每一类实例都需要学生列出相应的方程关系式，在已知量、未知量中建立等式关系.通过教材例题，学生可以及时应用一元二次方程知识，训练自己的认知水平，丰富自己解决数学问题的经验.为了进一步优化学生的数学思维能力，我也及时设计了专项一元二次方程应用题，基本都是以学生们熟悉的生活问题为背景，引导学生积极参与数学建模与问题解决活动.当然，由于本班学生的数学认知能力不同，所以我也注意调整了问题难度，以易、中、难三个层次保证本班学生都能积极参与方程训练.待学生完成数学练习之后，我会将6个学生分成一组，引导学生在小组内初步纠正不当答案，进而再实施培优辅差，落实练习辅导.

总而言之，例题是初中数学教材的宝贵资源.初中数学教师应该要积极突出学生在例题解析活动中的主动权，鼓励学生积极思考与主动创新，促使学生在例题学习中提升自身的数学解题能力.