多层玻璃窗应用于严寒地区宿舍的实测与模拟分析

汪秋刚， 李 靖， 额热艾汗， 任玉成

(石河子大学 水利建筑工程学院/给水排水工程系，新疆维吾尔自治区 石河子 832002)

0 引言

空气夹层被广泛应用于现代建筑围护结构中，如构造多层外门、多玻窗、通风窗、中空复合外墙、双层幕墙、Trombe墙、太阳能烟囱、通风光伏墙等[1]。外窗热损失在建筑能耗中的比例一直高居不下，多层玻璃窗结构无论是冬季保温，还是夏季隔热都被广泛认为具有较大的节能潜力[2-3]，在多层窗结构中，包含一层或多层的封闭空气夹层，利用空气的低导热系数增强整体保温性能；多层窗玻璃材质及厚度、空气夹层厚度、高宽比、温差都对传热系数都有很大的影响，学者们在这方面已经做了大量的工作[4-5]。

目前的研究基本上是对窗户单独的分析，因此，本文选取位于严寒地区的新疆石河子大学一有正常人为活动的单人宿舍，供暖初期在双层窗不同打开方式下进行了实测，分析了双层窗对室内热环境的影响。此外，利用数值模拟软件构造了多种类型的窗户，并进行了分析。

1 实测及分析

1.1 测试对象及方法

测试对象位于石河子大学建于2000年的宿舍楼，该楼窗户全部采用两层钢框玻璃窗夹空气腔的结构，散热器采暖，测试宿舍结构示意图如图1所示。

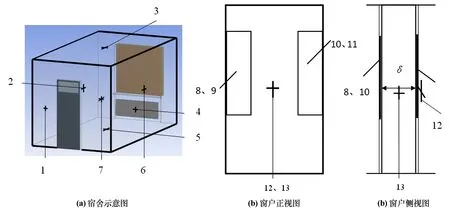
图1 宿舍结构及测点示意图

1—前墙测点；2—左墙测点；3—屋顶测点；4—散热器测点；5—地面测点；6—右墙测点；7—室内测点；8—左侧外窗；9—左侧内窗；10—右侧外窗；11—右侧内窗；12—窗内玻璃测点；13—空腔内测点

测试宿舍位于顶层，进深5 700 mm，宽3 000 mm，高3 100 mm，南向开窗，尺寸为1 740 mm×1 740 mm，空气夹层厚度为150 mm，其上布置四扇可独立打开的窗户。

测点布置参考《民用建筑室内热湿环境评价标准》[6]，各壁面度传感器布置在被测壁面中心，散热器温度传感器布置在肋片上，室内环境测点在宿舍中心，距地面1.4 m处，窗户空腔夹层温度传感器布置在中心，所有的温度传感器以铝箔纸覆盖，以减小周围壁面对其的辐射影响；此外还在室内测点及空腔内测点布置了微风仪；温湿度一体变送器用来测量室内相对湿度，置于室内环境测点，实测图如图2[7-8]。

图2 室内热环境实测图

温度传感器采用的是三线制、A级精度的PT100；空气流速的测量采用的是SNW-F3热线式室内微风传感器，量程0～5 m/s，测量精度0.2%FS，分辨率为0.05 m/s；温湿度变送器的型号是壁挂式的MIK-3TH；数据通过NHR-8700B蓝屏无纸记录仪自动采集。

在供暖初期，2017年10月28日～11月12日对双层窗在不同打开方式下室内热环境进行了实测，具体参数包括室内温湿度，室外环境温度，散热器及各维护结构内壁面温度，同时采集室内及双层窗空腔气流速度；数据每5 min钟自动保存一次。窗户打开方式整体分为封闭和通风两种形式，封闭环境有三种情况：10月28号8点40～31日8点40，窗户完全关闭；10月31日8点40～11月2日8点40，开启外侧两扇窗户；11月2日8点40～5日9点40，开启内侧两扇窗户。通风时具体情况为：11月5日9点40～8日9点40，开启左边外窗和右边内窗；8日9点40～10日0点，四扇窗户全部打开；10日0点～12日9点，开启右边两扇窗。

1.2 测试结果与分析

从图3可以看出，窗户封闭时室内温度波动较小，每日在15点左右达到最大值，平均温度21.4 ℃，最低为20.4 ℃，最高为23.6 ℃。室内相对湿度平均值为39.3%RH，最低为27.1%RH，最大为51.6%RH，波动较大，其波动趋势与室内气温的变化相反，查询活动记录，发现自然现象(降雨)和人为因素(洗漱)都能引起相对湿度大幅度的变化。期间散热器平均温度31 ℃，环境平均温度为10.3 ℃，室内、外平均温差10.1 ℃。

图4为三种不同通方式下，热环境相关参数情况。可以看出，室内温度出现了较大的波动，室内平风均温度为19.2 ℃，最大为24 ℃，最低时降到了15.2 ℃，仅开启两扇窗户时波动不明显，窗户全开时室内温度波幅达到了6 ℃。室内相对湿度平均值为33.1%RH，最低为28.4%RH，最大为39.2%。期间散热器平均温度29.2 ℃，环境平均温度为8.1 ℃，最大达到了18.7 ℃，室内、外平均温差11.1 ℃。

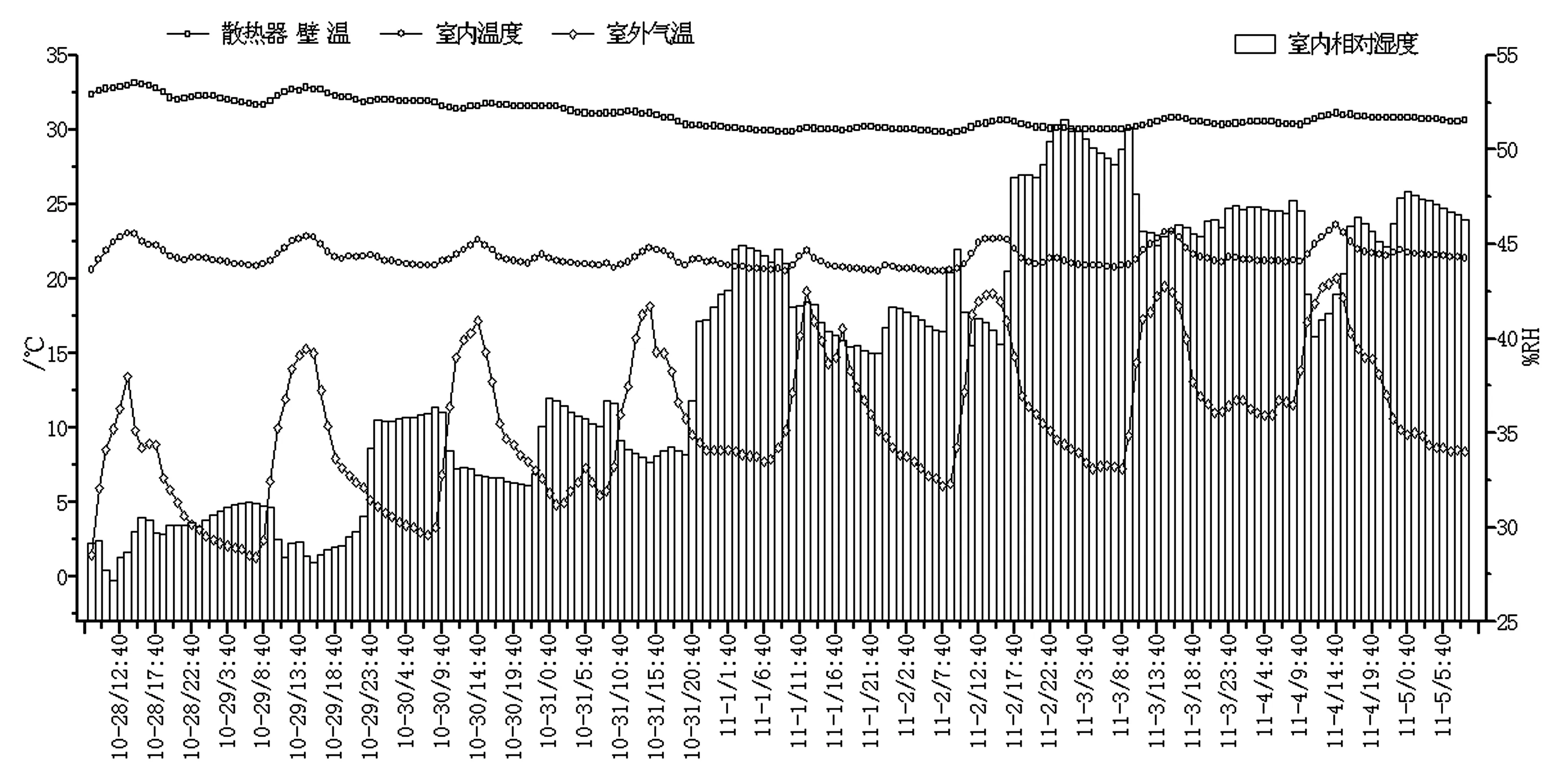
图3 封闭时热环境相关参数逐时曲线

图4 通风时热环境相关参数逐时曲线

房间周围壁面与人体之间产生的辐射换热对人体的冷热感觉影响很大，较低的壁面温度会对人体产生吹风感，令人感觉不舒适[9-10]。图5和图6分别为封闭和通风下，室内各壁面温度变化情况。封闭时，屋顶壁面平均温度为19.4 ℃，地面平均温度为22.2 ℃，玻璃窗内壁最低温度13.2 ℃，最高温度为39.2 ℃；通风时，屋顶壁面平均温度为18.2 ℃，最低时降到了15.7 ℃，地面平均温度为20 ℃，最低为16.8 ℃，玻璃窗内壁最低温度12.9 ℃，最高温度为38 ℃。可以看出，各壁面温度整体变化趋势是一致的，玻璃窗壁温波动最大，除玻璃壁外，屋顶始终是温度最低的地面，前墙次之，地面拥有最高的壁面温度。

对室内空气流速的监测结果显示，无论窗户封闭时还是通风条件下，室内空气流速不会超过0.1 m/s，主要是测试期间门一直处于关闭状态。

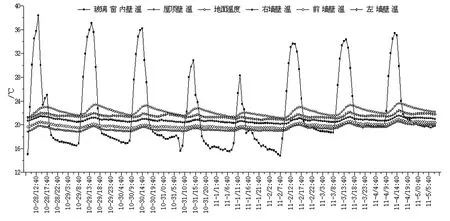
图5 封闭时时围护结构壁温逐时曲线

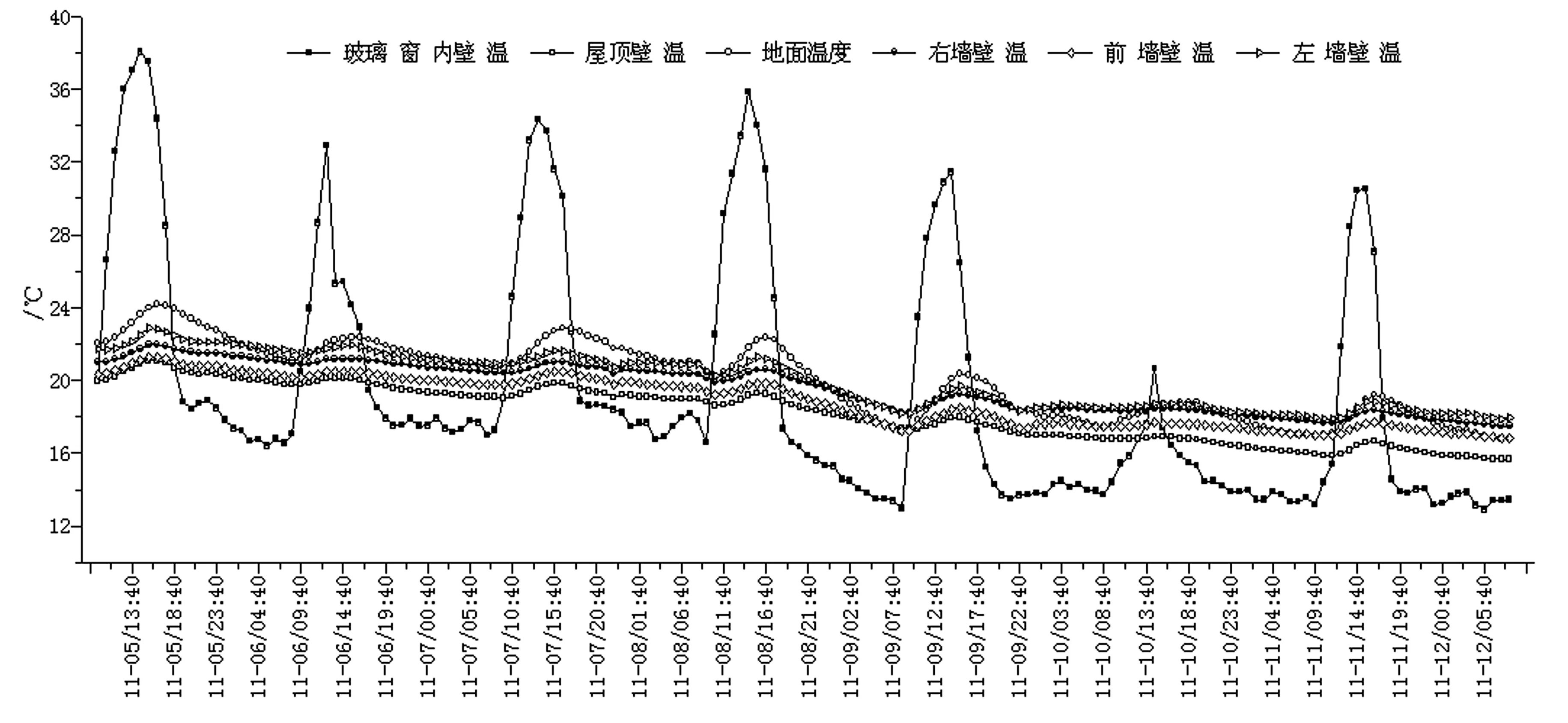
图6 通风时围护结构壁温逐时曲线

为进一步比较不同模式下通过各主要散热面的热量损失，对封闭时的散热量进行了分析，基于如下几个假设：

(1)室内空气与壁面的对流换热方式为大空间自然对流模式；

(2)各围护结构主要散热面温度均匀且为测点值；

(3)室内温度场均匀且为测点值。

玻璃窗及墙壁被视为竖平板，定性温度采取流体和壁面的平均值，特征长度取窗及墙高，屋顶被当做冷面向下的水平板来处理，地面当做热面向上的水平板来近似，特征长度采取当量长度，由式(2)得到，对流实验关联式为式(1)，所求得的Num为壁面的平均值[11]。

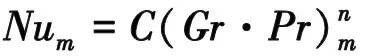
(1)

(2)

式中，

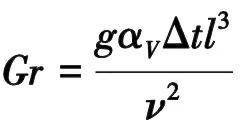
(3)

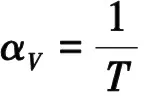
(4)

则，

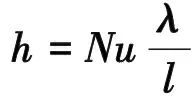
(5)

散热量，

Q=hAΔt

(6)

式(1)～(6)中Nu为壁面的努塞尔数；Gr为判断自然对流状态格拉晓夫数；Pr为定性温度下流体的普朗特数；L为水平板当量特征长度，m；Ap为平板换热面积，m2；P为平板周长，m；αV为体积膨胀系数，1/K；Δt为换热温差，℃；ν为流体的运动粘度，m2/s；h为壁面传热系数，W/(m2·K)；λ为定性温度下额流体导热系数，W/(m·K)；l为特征长度，m；Q为换热量，W。

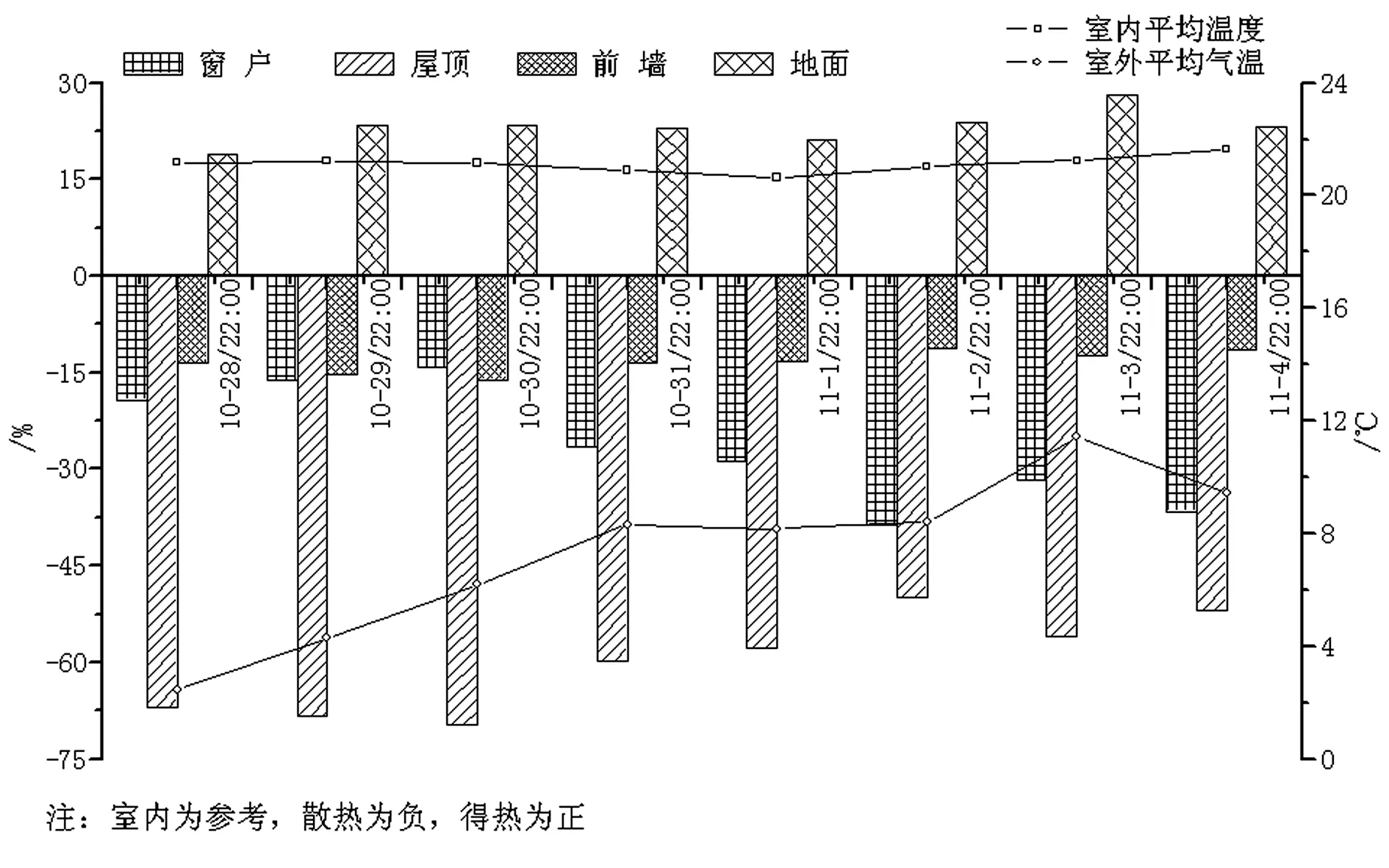
图7 夜间室内外温度及维护结构传热情况

对封闭环境下晚上10点～次日早上8点之间各维护结构的传热量进行了分析。结果如图7，窗户夜间散热情况与室外气温有相反的变化趋势，4扇窗户全部关闭时，通过窗户及前墙的散热量是相当的，通过屋顶的热量损失最大，占到了总散热量的68%左右，约为窗户散热量的4倍，通过地面楼板的得热量与总散热量相比，在22%左右。开启外侧两扇窗户时，通过窗户的散热量有明显的增加，占到了总散热量的27%左右，前墙的散热量占13%左右，通过地面楼板的得热量与总散热量相比，仍为22%左右。当内侧两扇窗户打开时，通过窗户的散热量占到了35%左右，屋顶仍然是热损失最大的地方。

2 多层窗模拟

带有空气夹层的窗户，自然对流是空腔内热传递的主要方式，影响传热速率的因素有很多，与结构相关的主要是夹层的高宽比。因此，在ANSYS Fluent平台下对不同类型窗户的传热性能进行了分析，为便于描述，窗户在竖直方向上分为单框、双框及三框，水平方向上分为单层、双层及三层(空气腔层数)，即目前实验对象的窗户结构可以称之为单框单层窗户。为深入了解窗厚δ的影响，在不同δ下，模拟了假想的纯导热状态，并与实际自然对流做了比较。

2.1 窗户物理模型

根据自然对流特性，将窗户简化成二维模型，为了保证现有的采光面积，高度始终为1 740 mm，改变窗厚δ、窗户空腔层数及框数来进行分析，窗框采用铝合金材料，对于双层及三层窗内部玻璃为3 mm。

壁面边界条件给的是第一类边界条件，高、低温壁面温度分别恒定为293 K、273 K，上下壁端部绝热，流体密度采用incompressible-idea-gas，其密度由式(7)确定，湍流模型选用RNG k-e模型。采用非定常计算，计算域初始温度同低温侧，为273 K，非稳态计算的迭代步长时间用式(8)估计；定性温度取平均值。利用ICEM CFD对空气夹层进行网格剖分，采取非均匀网格节点，壁面处加密，压力插值方案选择PRESTO！格式，压力-速度耦合方程用SIMPLE算法，动量、能量方程选用二阶迎风格式。

(7)

(8)

式中：ρ0为操作密度；Pop为操作压力；M为介质摩尔质量；R为气体常数，J/(mol·K)；T为热力学温度，K；L为特征长度，对封闭腔传热取夹层厚度δ，m；β为流体体胀系数，1/K；g为重力加速度，取9.8 m/s2；ΔT为换热温差。

2.2 模拟结果与分析

2.2.1 窗户封闭夹层流场特性

图8是不同窗户在稳态时的温度云图，从左到右依次是纯导热状态，单框单、双及三层窗，双框单、双及三层窗，三框单、双及三层窗。可以看出，窗户的分层，使得整个二维温度场在横向形成了高、低温分段，封闭腔自然对流等温线整体表现出“三段式”特点，即两侧靠近壁面区域，等温线接近于竖直，远离壁面区域，等温线接近于水平，且高宽比越小，这种特点越明显，高宽比越大，等温线越接近于一条倾斜的直线；纯导热状态的等温线是等间距的与竖壁平行的直线，温度梯度垂直等温线，沿水平方向。图9显示了δ为150mm的单框单层窗870mm处沿厚度方向温度及速度的变化，可以看出，温度的变化仅发生在紧靠两侧壁面的区域内，远离壁面的区域水平方向的温度梯度为零，即该区域内没有水平方向的热量传递；速度曲线呈“M”形，在边界层内具有最大的速度梯度，根据传热学知识，在贴壁无滑移边界条件下，热量只能以导热的方式穿过这个流体层；因此，整个腔体的传热过程为：高温侧壁面通过边界层以导热的方式将热量传递给上升的热流体，流体在低温侧受到冷却而下降，空气以环流的方式在高温侧和低温侧间流动换热。

图8 不同类型窗户温度云图

图9 高870 mm处的温度及速度分布图

2.2.2 传热系数h的变化

不同层数单框窗户的传热系数h与δ的关系如图10，δ在250 mm与45 mm之间时，各层窗户的传热系数h基本保持不变，同厚单层窗的h最大，双层窗次之，三层窗最小，即三层窗的保温性能最好；继续减小δ，各层窗户的h都明显地增加，双层与三层窗间的h基本相同，仍小于单层窗的，当δ小于15 mm后，h急剧上升，单层、双层及三层窗间的h趋于相同。

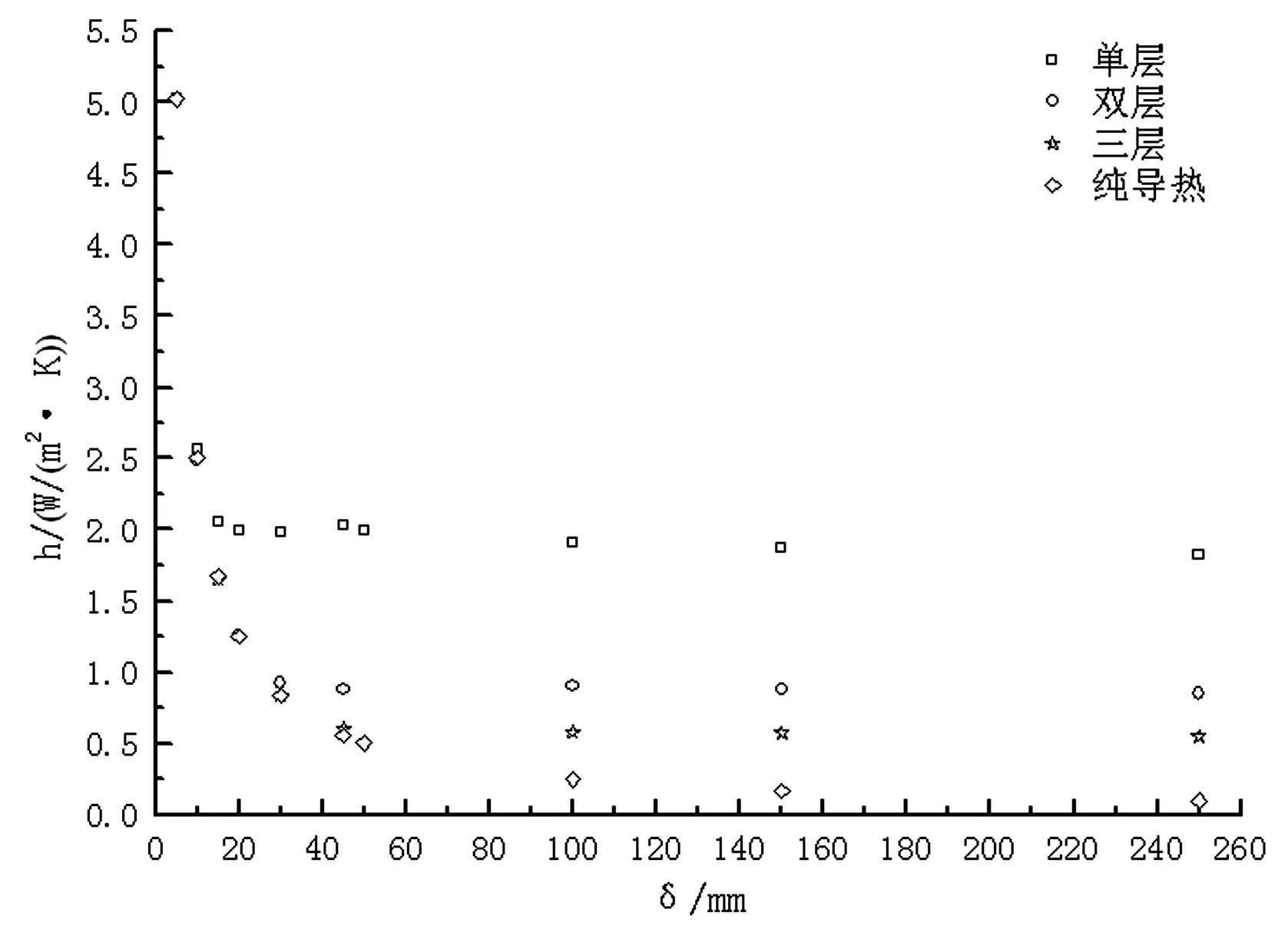
图10 不同窗厚δ下的传热系数

各类窗户空腔内的最大速度如图11，单层窗umax最大，三层窗最小，可见，正是窗户的分层限制了窗内自然对流的发展，从而减小了h，起到了更好的保温作用。

图11 不同窗厚δ下的流场最大速

假想纯导热状态下的传热系数在一定程度上能够反映一个对流传热问题中导热依靠导热传递的能量，以竖夹层Grδ来判断自然对流的状态，指出当Grδ≤2 860时，空腔内部热量依靠导热，根据已知条件求得这个临界δc为9.4 mm，与图10及表1显示了良好的一致性。当δ小于45 mm后，umax急剧下降，但整体h是增大的，结合图10可以发现，这主要是由于随着δ的减小导热在对流传热中的作用越来越明显，到δ为10 mm时，纯导热下h与δ单层窗几乎相等。

进一步对双框与三框不同层数、不同δ下的窗户进行分析，发现框数对h的影响可以忽略，表1是双框与三框不同窗户的h值，对比发现，双框与三框窗户h随δ及层数的变化规律与单框是相同的。对于双框窗当δ为250、150、100、45、30、20、10 mm时，双层窗h分别为单层窗的46%、47%、46%、45%、48%、66%、97%；当δ为250、150、100、45、30、15 mm时，三层窗h分别为单层窗的30%、30%、29%、32%、45%、83%。因此，根据以上分析，考虑到实际生产和使用方面的因素，厚为45 mm三层玻璃窗是最理想的窗户类型。

表1 不同类型窗户下的传热系数值

3 结论

(1)测试得知，封闭环境下该宿舍具有良好的热工性能，供暖初期，环境温度在0～20 ℃波动时，散热器温度保持在30 ℃左右时，就足以使得室内平均温度维持在21 ℃左右，日波动幅度不超过3 ℃，室内热环境稳定。仅开启两扇窗户时室内温度波动不明显，窗户全开时室内温度波幅达到了6 ℃。室内相对湿度受自然因素和人为活动的影响，会出现较大的波动。

(2)窗户封闭时对夜间通过各围护结构的热量进行分析，窗户完全关闭时，通过窗户的散热量占22%左右，外侧两扇窗户开启时，其值增大为27%，开启内侧两扇窗户时，窗户散热量占到了35%左右。

(3)对构造的窗户在ANSYS Fluent下分析得到，多层窗在竖向的分段，即框数对传热系数的影响很小，可忽略不计，多层窗在横向的分层，即空气腔的层数对多层窗传热系数有成倍的影响，在所构造的窗户类型中，三层窗具有最好的保温性能。通过计算，若采取改进的三层窗结构，现有窗户的散热损失能减少60%以上，从而大大减少冬季的供暖能耗，实现节能。