基于多层感知机的温室内番茄茎直径变化预测模型
陈毅飞,杨会民,马 艳,张新伟,喻 晨,王学农
(1.新疆农业科学院农业机械化研究所,乌鲁木齐 830091;2.新疆农业大学机电工程学院,乌鲁木齐 830052)
0 引 言
【研究意义】气候干旱与水资源匮乏是新疆的主要地域特征,伴随着农业种植面积不断扩大,水资源利用过度等问题,开发合理有效的灌溉策略及设备将具有更加重要的研究意义[1-3]。现代智能灌溉决策系统需要掌握作物的需水规律[4],目前作物需水规律主要有两大类诊断方法,一类是测量表征作物本体需水状况的指标[5, 6],主要为蒸腾系数及蒸腾量、光合速率、叶水势、茎秆径流和叶片膨压等[6, 7],但目前采集上述生理指标的传感器存在检测设备昂贵,叶水势、气孔导度等部分传感器对作物有不可逆转的破坏性,且难以实现实时在线监测,需要人工进行采样通过手持设备或实验室仪器进行检测[6, 8-10]。另一类主要是采集环境信息及测定土壤含水量的方法[11],市面上采集土壤含水量的传感器种类繁多,测量较为直接并且可以在线实时监测利用较为广泛,但是缺乏对作物本身需水情况可靠信息的测定,在实际应用中主要由人工对数据进行判断再得出灌溉决策[11-13]。【前人研究进展】目前国内外主要采用环境数据监测及预测作物茎直径变化的方法建立作物需水模型。国内王晓森等[14, 15]结合茄子及番茄不同生育期茎直径变化特征与气象因子采用了统计分析的方法进行了相关性研究并建立了茎秆变化多元回归方程,提出了针对茎秆成熟期的茎秆变化预测模型并取得了较好的成果。员玉良等[16]结合温室环境数据与茎秆变化数据采用了主成分回归的分析模型对番茄与向日葵的茎直径进行了预测,并取得了良好的预测效果国外。Gallardo等[17]利用茎秆变化传感器进行茎秆日变化量(TDF)的数据采集并将TDF测量应用在小茎秆草本植物的灌溉策略的制定中,Moreno等[18]将TDF测量方法应用在橄榄树等大型木本植物中并建立了基于TDF测量方法的灌溉策略。González Perea R等[19]通过分析番茄日空气温湿度、日土壤温湿度及风速等环境信息提出了基于自适应神经模糊算法的番茄灌溉等级预测模型。Olutobi Adeyemi等[20]基于高斯分布型贝叶斯估计算法针对温室生菜提出了植物叶片蒸腾速率数据驱动型预测模型,预测短时间内的作物蒸发速率进而判断作物是否存在水分亏缺状况并取得了较好效果。Anat Goldstein等[21]对荷荷巴树果园进行了环境数据采集并采用了提升决策树的机器学习方法对环境数据及土壤数据进行了数据挖掘提出了针对荷荷巴树的灌溉策略。以色列Phytech公司及B.F.Agritech公司已经研发出了基于果树茎秆变化及果实变化的果园关键变量自动监测系统[9],在以色列已商业化运行并取得了较好的成果,B.F.Agritech公司目前已引入国内并与国内私企联合开发基于茎直径变化的用于商业运作的设施番茄灌溉设备及策略。【本研究切入点】国外学者研究对象多为果树及大田作物,很少以温室作物为研究对象,国内学者的研究主要以基础研究为主,研究方法及手段较为单一且繁杂无法进行动态实时预测,较少有将环境信息与植物生态信息进行融合的研究。针对温室内番茄需水规律的模型参数不确定及系统非动态分析的问题研究文献不多。实际的温室作物需水模型预测往往存在诸多影响因素,需要模型及时调整控制参数进行校正并能过滤无关数据扰动,要求温室作物灌溉策略既能保证系统具有较强的鲁棒性,又能保证系统具有自适应性。【拟解决的关键问题】以温室番茄为研究对象,将一个生长周期采集的空气温湿度、土壤温湿度、太阳辐射等环境信息与叶片温度、茎秆变化值等植物本体数据集分成训练数据集、验证数据集及测试数据集,采用多层感知机(MLP)算法对环境与植物生态数据相融合的数据集进行训练并得到番茄茎秆变化短期(8 h以内)预测模型,为番茄智能灌溉策略提供进一步的数据决策支持。
1 材料与方法
1.1 材 料
2018年11月4日~2019年2月27日,试验在新疆农业科学院农业机械化研究所Venlo型铝合金玻璃温室(43°48′39.6″N,87°34′33.12″E)进行,一共种植了56株生长期相同的盆栽番茄样本,抽取了2株生长状态相似且同处于结果期的盆载番茄样本,番茄品种为天粉一号,所用花盆容量为10 L,规格为0.35 m(底)×0.3 m(高),采用基质栽培的方式,基质为草炭、蛭石和珍珠岩按3∶3∶1的比例混合而成,初始基质肥料含量为有机质58.62%、速效氮638.9 mg/kg、速效磷371.3 mg/kg、速效钾6 640 mg/kg。
利用植物生理生态数据采集系统(PM-11,Israel,BF-Agritech)每隔10 min连续自动采集环境数据与植物生理数据,主要指标为空气温度、空气相对湿度、土壤湿度、太阳有效辐射、叶片温度、茎秆直径变化。表1
温室内2株番茄的茎直径每天都会进行周期性变化,在水分供给正常时会有不同程度的增幅。试验将选取番茄结果期数据的茎直径变化量作为预测指标,LVDT传感器分别安装在距基质表层3~5 cm处连续监测茎直径变化,一共安装2个。番茄整个生长季共采集了72 800条数据,主要选取番茄结果期22 400条数据进行模型的建立及预测研究,并根据交叉验证原则按7∶2∶1的比例将数据集分成了训练集、验证集和测试集具体数据条数。图1,表2
1.2 方 法
1.2.1 MLP模型结构
采用多层感知机(MLP)进行茎直径变化非线性回归分析,MLP 是深度神经网络(DNN)中一种比较有代表性的前向结构人工神经网络。MLP在处理大样本量时,学习能力优于单层感知机与主成分分析法[22, 23]。误差逆传播(error Back Propagation,简称BP)算法将使多变量非线性回归问题的处理变得更加简化。通过建立MLP输入层、隐藏层、输出层三级网络结构,在前人的研究基础上将筛选之后的数据集输入网络中进行回归训练[24, 25]。最后通过确定每个输入节点与后面隐层之间的权值与偏置系数得到描述目标对象特征的预测模型,即茎直径变化。
表1 植物生理生态数据采集系统性能指标
Table 1 The Performance index of Plant physiological and ecological data collection system

测量参数Measurement Value型号Type精度Precision分辨率Resolution测量范围Measurement Range空气温度Air TemperatureATH-3ZT±0.5℃0.1℃-40~60℃空气相对湿度Air Relative HumidityATH-3ZH±2%RH0.1%RH3%~100%RH土壤湿度Soil MoistureSMTE-3Z±2%VWC0.1%VWC0~100%VWC太阳有效辐射Effective Solar RadiationPIR-1Z±5%1 μmol/(m2·s)0~2 500 μmol/(m2·s)叶片温度Leaf TemperatureLT-4Z0.1℃±0.2℃0~50℃茎秆直径变化Stem Diameter VariationSD-5Z±0.1%0.002 mm0~5 mm
注:VWC为体积含水量
Note:(Volumetric Water Content)
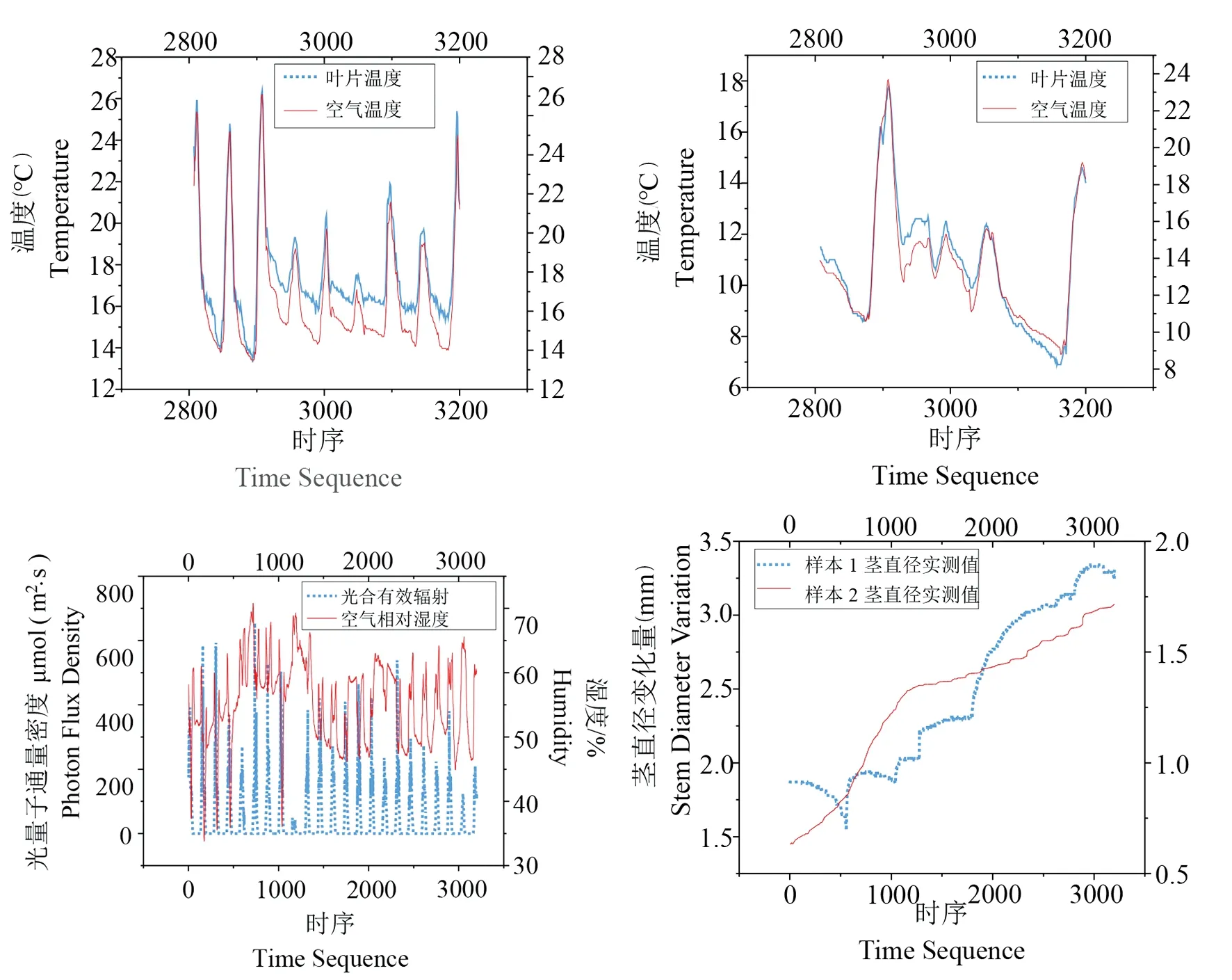
图1 番茄样本1和2环境及植物本体数据趋势
Fig.1 Trend of Environmental and Ontology data of tomato samples 1 and 2
表2 训练集、验证集和测试集条数
Table 2 Training Set, Verification Set and Test Set
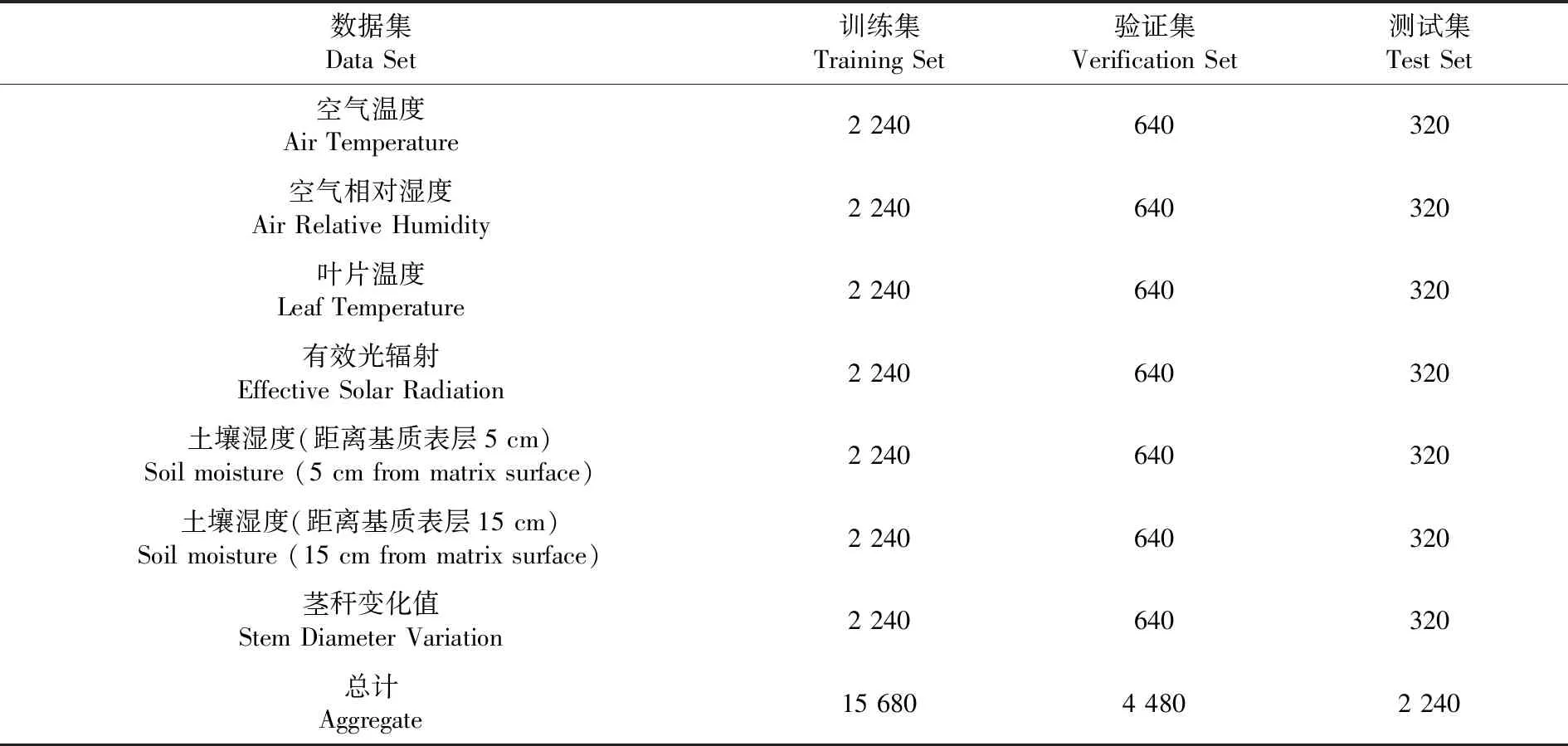
数据集Data Set训练集Training Set验证集Verification Set测试集Test Set空气温度Air Temperature2 240640320空气相对湿度Air Relative Humidity2 240640320叶片温度Leaf Temperature2 240640320有效光辐射Effective Solar Radiation2 240640320土壤湿度(距离基质表层5 cm)Soil moisture (5 cm from matrix surface)2 240640320土壤湿度(距离基质表层15 cm)Soil moisture (15 cm from matrix surface)2 240640320茎秆变化值Stem Diameter Variation2 240640320总计Aggregate15 6804 4802 240
1.2.2 MLP模型结构及训练算法
选取训练集数据中的空气温度、空气相对湿度、土壤湿度、叶片温度及有效光辐射等数据作为MLP模型的数据输入,茎直径变化量为已标定的目标输出值,建立以茎直径变化量为目标函数的多层感知机非线性回归模型[16]。MLP模型有多个节点层组成且为全连接,第一层是输入层,最后一层是输出层,中间称为隐含层,每一层包括确定数目的神经元。图 2

图2 多层感知机模型结构
Fig.2 Structure of Multi-Layer Perceptron Model
图1中输入层共有 6个输入变量(x1,x2,…,x6),通过sklearn平台中Grid SearchCV超参数网格搜索算法对3个隐含层进行参数优化得到各个隐含层的神经元数量(L(1):q个,L(2):p个,L(3):r个),输出层有 1个神经元(y),除去输出层,每一层均有一个偏置项(b1,b2,b3)。基于sklearn平台搭建的茎直径变化非线性回归分析的MLP模型,共构建了3层隐层,隐层节点分别设置为(100,30,30),具体MLP算法建立步骤如下。图1
1.2.2.1 输入

1.2.2.2 数据归一化
采用线性归一化函数将数据转换到[-1,1]之间,计算公式[26]如下:
公式中x表示样本数据,xmax和xmin分别表示样本数据中的最大值和最小值,y表示归一化后的数据,ymax和ymin分别表示归一化后数据的最大值和最小值。
1.2.2.3 数据L2正则化
在最小化残差平方和2 421的基础上加入L2范数的惩罚项使某些系数的估计为0,此dropout机制的引进可以降低过拟合的风险,公式中p为引入的p个预测变量,具体计算公式[27]如下。
(2)
(3)
1.2.2.4 循环遍历计算从输入层依次到隐含层到输出层的每个节点
每个节点的计算方法[18]如下:
xij=f(WiXi-1+bi-1).
(4)
式中:xij代表第i层第j个神经元的值;Wi为第i-1层到第i层第j个神经元的权值向量;Xi-1为第i-1层所有神经元的值向量;bi-1表示第i-1层的偏置;f为激活函数。激活函数采用ReLU函数:
f(x)=ReLU(x)=max(0,x).
(5)
1.2.2.5 参数估计通过Grid SearchCV超参数网格搜索算法[28]寻求并确定最优参数
使得MLP算法损失函数达到最小时停止计算,损失函数定义为:
(6)
式中h为MLP输出值;y为实际值;-2代表距离为2的范数。
1.2.2.6 经过全连接层计算后输出y值,经过反正则化与反归一化后得出茎秆变化预测值[29]
将预测值与实际监测值通过公式(7)与公式(8)对模型进行准确率与相关性的计算,最终完成茎秆直径预测模型的验证与评估工作进而判定该模型是否有效。
1.2.3 MLP模型预测与评估
将验证集代入到已建立的MLP模型,经过全连接层计算后输出y值,经过反正则化与反归一化后求出茎直径变化量的预测值[30]。对模型进行准确率与相关性的计算,最终完成茎秆直径预测模型的验证与评估工作进而判定该模型是否有效。同时将误差反馈回MLP模型并进行纠正,最终在不断地迭代搜索中获得改善后的MLP模型并得出均方根误差(Root Mean Square Error,简称RMSE),计算公式[31]:
(7)
公式中Ypre,i是第i条验证数据集的模型茎秆变化预测值,Yobs,i是第i条验证数据集的茎秆变化实际测量值,n是输入验证数据集的条数。最后将测试集带入改善后的MLP模型求出茎直径变化量的预测值并与实测值计算得出实际使用后的RMSE与回归系数(R2)用来评价已建立的MLP模型,R2计算公式[16]如下所示:
(8)

2 结果与分析
2.1 模型验收
采用Grid SearchCV超参数网格搜索算法参数寻优确定MLP模型中的隐含层数量、优化容忍度、激活函数、学习率等参数的最优组合[31],获得模型训练样本的R2值和RMSE值,根据R2值和RMSE值的大小确定最合适的MLP模型。使用的模型共构建了3层隐层,隐层节点数分别设置为(100,6,6),激活函数为ReLU函数。
将训练集中的空气温湿度、土壤湿度、光有效辐射及叶片温度等值构成MLP模型的6维输入向量(模型的输入向量需要进行f2正则化及归一化操作),番茄茎直径变化量为MLP模型的输出向量(模型的输出向量需要进行反归一化操作),在sklearn平台中构建其训练模型,训练结果。图3

图3 短期数据进行的茎直径变化量预测值与实测值比较
Fig. 3 Comparison between the Predicted and Measured values of Stem diameter variation from short-term data
MLP非线性回归对于番茄训练样本1的R2值为91.27%,RMSE值为0.169,对于番茄训练样本2的R2值为91.41%,RMSE值为0.163,非线性回归模型的学习效果还是比较理想的,说明研究提出的基于MLP非线性回归预测短期番茄茎直径变化量是切实可行的。对构建好的MLP非线性回归模型对测试集进行预测,共抽取了8 h左右共50组数据进行模型验证。图4
模型的预测结果与观测数据吻合良好,能将番茄茎直径变化趋势较好的预测,预测样本的R2值为0.945,RMSE值为0.209。表3
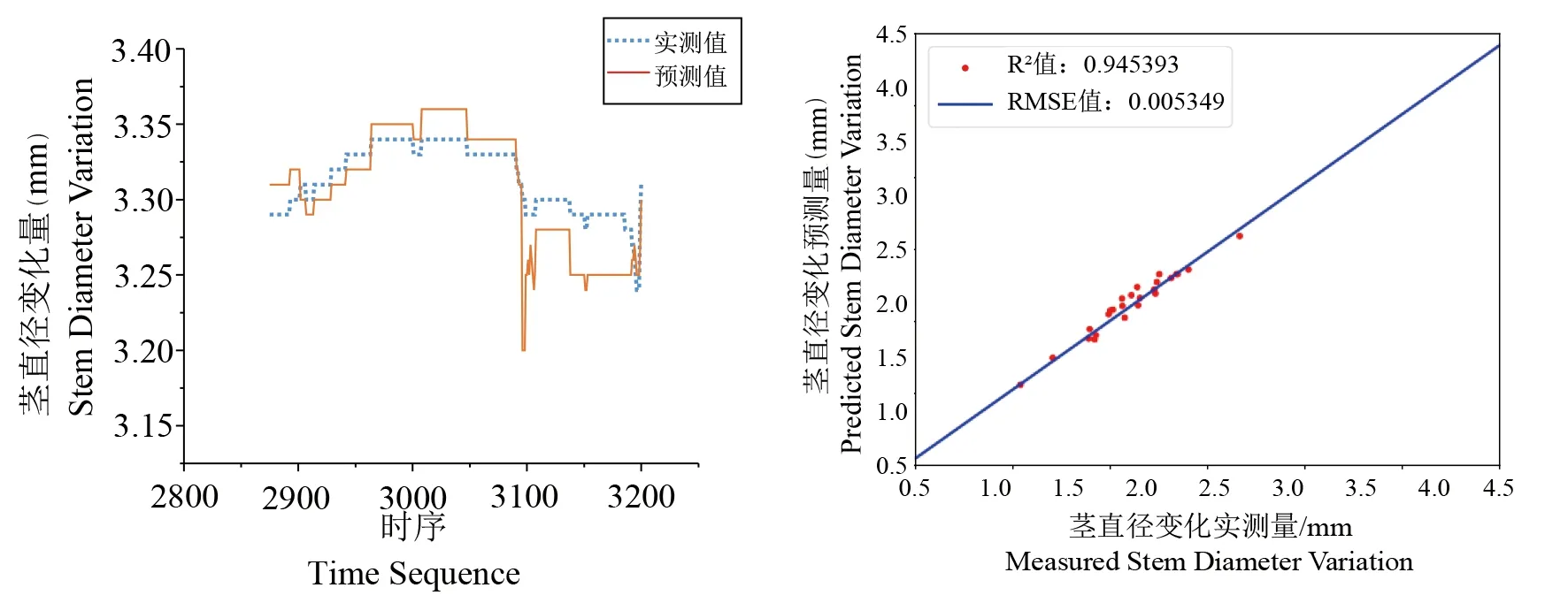
图4 测试集中茎直径变化量预测值与实测值比较
Fig. 4 Comparison between the Predicted and Measured values of Stem diameter variation in the test set
表3 部分试验数据
Table 3 Experimental data

时序Time Sequence预测值Predicted Value实测值Measured Value13.2643.29023.1993.13033.3333.34043.3323.34053.3383.34063.2843.29073.1253.12083.3113.30
2.2 模型评估
将试验获得数据集输入到MLP模型进行番茄茎直径变化量预测,并进行了5次随机数据抽取进行模型评估测试,最终将2个番茄样本共10次模型评估测试结果求平均值后得到模型最终评估结果R2:0.848,RMSE:0.20。表4
表4 预测值与实测值的误差
Table 4 Error between Predicted value and Measured value

样本SampleR2平均R2AueraneRMSE平均RMSEAverage番茄样本1Tomato Sample 10.9120.168番茄样本2Tomato Sample 20.8900.182
番茄样本1 的MLP非线性回归模型预测番茄茎直径变化量R2为0.912,RMSE值为0.168;番茄样本2的MLP非线性回归模型预测番茄茎直径变化量R2为0.890,RMSE值为0.182。该基于MLP非线性回归模型预测番茄茎直径变化量模型在番茄样本上的表现具有较高的预测精度,并具有较好的适应性。
3 讨 论
由于植物茎直径变化的影响因素来自环境因素、土壤含水量及植物自身生长发育等,因此,以处于生长缓慢期的番茄结果期的茎直径变化量为研究对象,利用多层感知机技术建立了一种短期番茄茎直径变化量多层感知机预测模型,该模型在前人研究的基础上选取了主要多种环境参数及植物本体参数并融合了深度学习算法,进而增加了模型的计算复杂度,此外选取参数的不足也会导致对预测结果有着不同程度的影响。
作物生长期的研究具有一定的局限性,基于MLP的番茄茎直径变化量预测模型的研究仅从结果期时间序列数据进行分析,而没有对番茄其他生长期及农艺等因素进行研究,例如果实成熟过程中需要进行一定的水分干旱胁迫防止番茄裂果,番茄定植初期第1次浇水后需要进行适量的干旱胁迫,这样更有利于番茄根部的发育。要准确预测番茄需水量,不能只考虑茎直径变化量的变化,应将外界环境、茎直径变化量、作物生长发育及农艺等因素共同考虑进行作物需水情景中建立有效的多模型融合的作物需水预测模型。
4 结 论
从生产实际出发,充分考虑番茄茎直径变化的动态特征,将多层感知机算法与植物本体数据及环境数据进行融合,以2018~2019年温室内番茄结果期实际采集数据为样本建立了短时间序列番茄茎直径变化量动态预测模型,动态预测和分析番茄结果期的茎直径的变化。该模型有效的将植物本体数据与多元环境数据进行了融合,更好的进行了番茄茎直径变化量的非线性拟合,相比以前单一的环境数据或植物生理生态数据的拟合技术,更能动态的描述茎直径变化的趋势。该MLP预测模型具有较好的预测精度,预测误差在可接受范围,具有一定的实用性,可用于新疆连栋温室内秋季番茄的茎直径变化量预测。

