基于有限元的飞轮电池转子系统振动分析与结构优化

秦 珅， 刘新华， 朱由锋

(1 山东中烟工业有限责任公司 青岛卷烟厂 ， 山东 青岛 266590)； 2山东科技大学 交通学院， 山东 青岛 266590)

0 引 言

飞轮电池是一种近年来兴起，利用转子旋转来储能的新兴物理电池，具有无污染、寿命长、维护成本低的优点，可广泛应用在交通、军工、航空航天等领域。由储能公式w=1/2·J·ω2可知，飞轮电池最大储能密度与转子转速大小成二次方关系。高转速下，转子质量偏心和磁场力分布不均的问题会增加转子系统的不稳定性[1]。转子系统运行转速与临界转速相近时，会产生振动加剧的共振现象，造成转子的失稳和变形，严重影响了飞轮电池的安全性和可靠性[2]。模态分析和谐响应分析能确定转子系统的固有频率和临界转速，为振动分析和结构优化提供了重要理论支撑。杨红进等通过ADAMS软件建立了飞轮转子与等效基础的机械模型，利用MATLAB软件建立了相应的不完全微分PID控制器模型，联合仿真分析了基础加速、减速、转弯和爬坡运动，以及因路面不平整引起的基础纵向振动、横向振动和俯仰振动对高速飞轮转子系统动态性能的影响[3]；吉利采用传递矩阵法，改变支承刚度值，计算出不同刚度条件下磁悬浮柔性转子的临界转速，得出了磁悬浮转子低阶临界转速与磁轴承支承刚度有关，高阶临界转速与飞轮转子有关的结论[4]；魏彤等提出了一种考虑功放环节α逆系统结合滑模控制器的解耦控制方法，成功消除了磁悬浮控制力矩陀螺径向磁悬浮转子强非线性、强陀螺效应耦合对系统稳定性的影响[5]；董淑成等对陀螺效应引起的转子失稳现象进行了实验分析，得出章动失稳由系统相位滞后引起，进动失稳由积分控制引起的结论，为控制系统设计、控制参数的选取提供了理论指导[6]。

有限元分析采用离散化方法，以实际工程模型和物理环境为中心，计算效率和精度都比较高[7]。Workbench软件具有集成性和参数化特点，能实现与CAE软件的高精度连接。本文采用Workbench软件对飞轮电池转子系统进行模态分析、谐响应分析和响应曲面优化分析。

1 模型建立

有文献作者设计的一款飞轮电池，结构如图1所示[8]。忽略能量转换转置、真空室的影响和对分析结果影响不大的工艺特征，如倒角、螺母等，在CATIA软件中建立了磁轴承轴套、电动机/发电机转子、推力盘和飞轮转子的三维模型，导入到Workbench软件中，如图2。

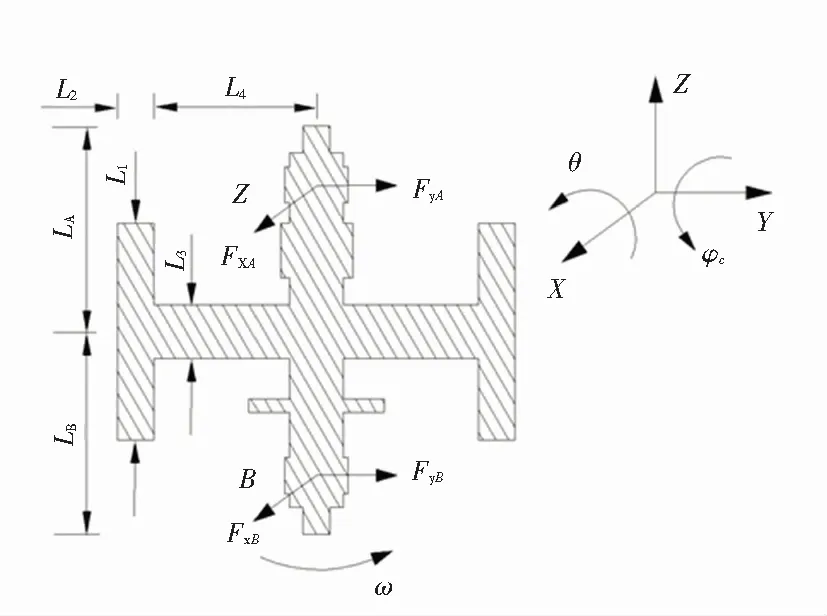
图1 飞轮电池结构图

图2 飞轮电池三维模型图

图1中，ω为转子转速，Mr为转子质量，θr为转子在yz平面内转角，φr为转子在xz平面内的转角，Jxr为转子绕x轴转动惯量，Jyr为转子绕y轴转动惯量，Jzr为转子的极转动惯量。A和B是磁悬浮轴承，LA为转子质心到轴承A质心的距离，LB为转子质心到轴承B质心的距离。L1为转子外环宽度，L2为转子外环高度，L3为轮毂宽度，L4为轮毂半径。

具体参数，见表1。

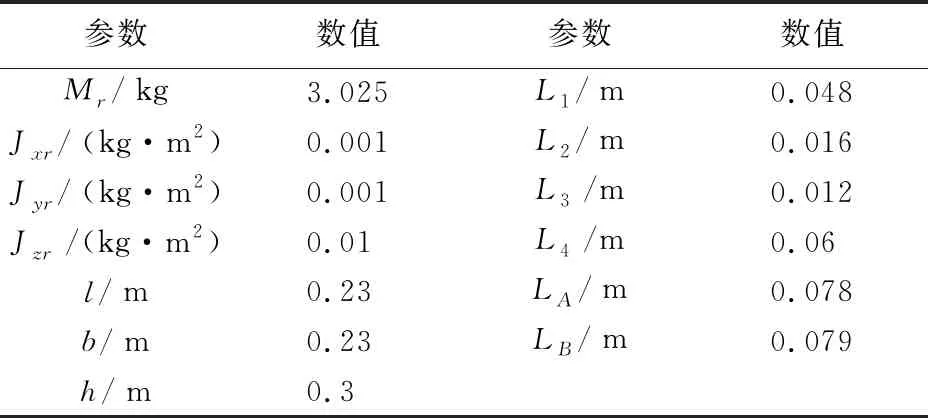
表1 飞轮电池相关参数

在engineering data选项中，为飞轮电池各部分添加材料属性。转子外环部分采用强度高、质量小的碳纤维复合材料T700。与转子外环结合的轮毂部分采用7075铝合金。推力盘固定在转轴上，采用纯铁材料。转轴及其它剩余部分采用合金钢。各材料属性详见表2。

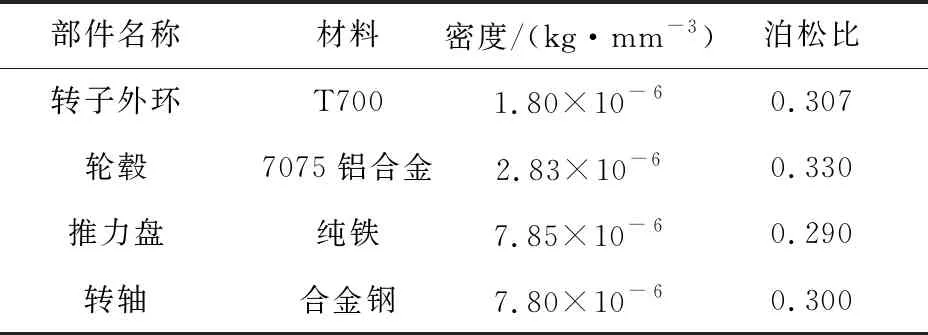
表2 转子系统各部件材料属性

网格划分质量好坏直接影响到软件求解精度和求解速度。网格尺寸太小，会增加电脑的计算时间和存储空间。飞轮转子是本文分析的重点，计算精度要高。转子外环和轮毂部分采用四面体网格划分方法中的Patch Conforming划分方法，网格划分细密，计算准确。转轴和其它部分采用自动划分方法。网格尺寸设置为默认，Relevance选项设置为50。飞轮电池模型划分网格后，节点数为111 860，单元数为63 394。模型如图3所示。

图3 飞轮电池网格划分

2 有限元分析

2.1 约束施加

飞轮电池竖直放置可有效抑制陀螺效应，系统稳定性高。采用磁悬浮轴承限制转子系统径向和轴向自由度。上下两端的保护轴承采用普通机械轴承。飞轮电池径向磁轴承与转轴之间，轴向磁轴承与推力盘之间都有微小间隙，转子系统旋转过程中会有径向和轴向的微小位移，将磁轴承近似成弹性支撑[10]，即将磁轴承约束等效成在Y方向和Z方向的弹簧约束。简化模型如图4所示。

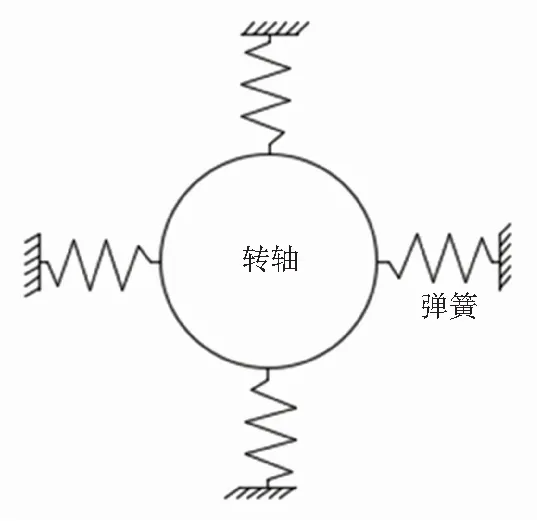
图4 磁轴承简化模型

磁轴承简化模型理解为外端是固定的定子，内端为自有约束的弹簧组成的弹性支撑。弹性支撑具有自由调节能力，与转子系统的位置密切相关，因在实际的工程应用中刚度可以灵活调整，在Workbench软件中将弹性支撑的Foundation stiffness选项设置为500 N/mm3，此时可以作为典型的柔性状态下的支持，贴近于磁悬浮轴承实际参数。施加载荷与约束后的模型，如图5所示。

图5 飞轮电池模型约束分布

2.2 有限元仿真

坎贝尔图横轴为转动角速度，纵轴为固有频率，其能确定旋转机械的共振频率和临界转速，非常适用于旋转机械的振动分析。

在workbench中将campbell diagram选项与coriolis effect选项分别设置为on，分别打开坎贝尔图项和陀螺效应项。在tabular data选项中设置转子系统初始转动角速度300 rad/s，最大旋转角速度为4 300 rad/s，步长为1 000 rad/s。

2.3 结果分析

飞轮电池磁悬浮转子系统前两阶振型图和坎贝尔图，如图6所示。转轴末端是转子系统变形较大的地方，进行谐响应分析时，不平衡力应施加在此处。

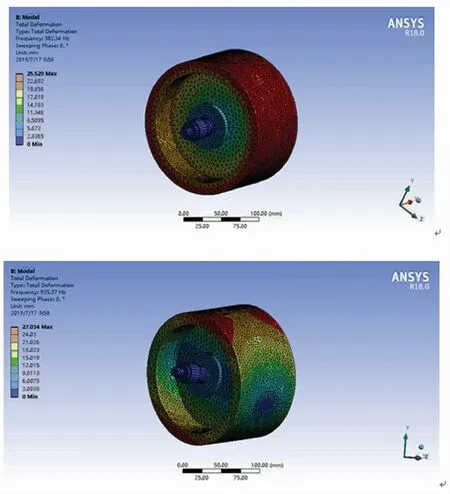
图6 磁悬浮转子系统前两阶振型图

弹性支撑为500 N/m3时，飞轮电池磁悬浮转子系统的坎贝尔图，如图7所示。黑色直线是设定的转速曲线，与彩色直线的交点是临界转速。进动有正进动和负进动。正进动更容易引起转子系统，负进动也不可忽略。磁悬浮转子系统的前两阶固有频率和临界转速见表3。

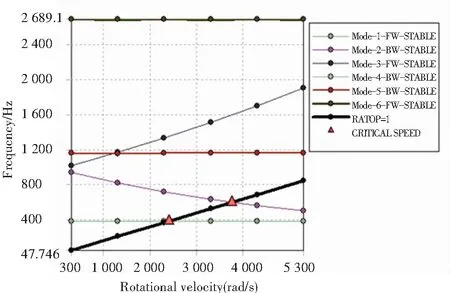
图7 坎贝尔图

表3 转子固有频率和临界转速

3 谐响应分析

飞轮电池转子材料的各向异性以及制造工艺的限制，会使转子质量分布不均匀。高速旋转时，会产生不平衡离心力。

如图8，Os，Or，Om分别为转子形心、旋转中心和质心，ω是转子转动角速度，OrOm=e1，OsOm=e2分别是旋转轴到质心的距离和偏心距。oxy是主动磁轴承坐标系，Orξη是转子自转坐标系。偏心距与转子自转坐标系ξ轴夹角为φ。

则，不平衡力简谐力表达式为式(1)和式(2)：

fx=Mreω2cos(ωt+φ),

(1)

fy=Mreω2sin(ωt+φ),

(2)

其中，e=e2-e1。

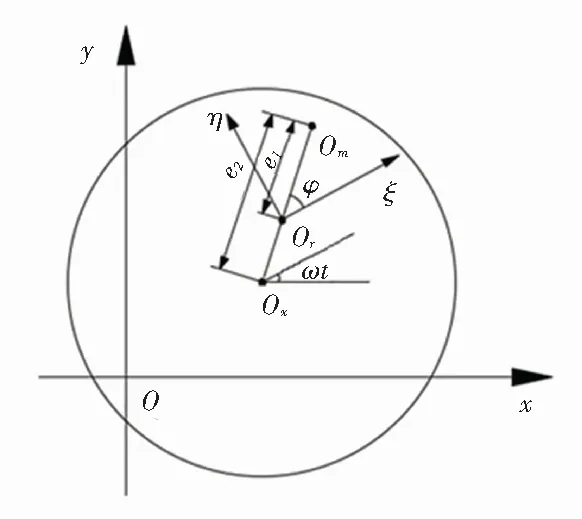
图8 转子不平衡示意图

前面模态分析已经得到转子的前两阶临界转速，考虑到转速越高，系统响应越剧烈和复杂。故主要研究当转子转速ω=3 700 rad/s时，飞轮电池转子系统的振动响应。

计算求得，对转子施加的不平衡简谐力为式(3)和式(4)：

(3)

(4)

飞轮电池转轴施加不平衡力后，转子表面，电机转子表面和前、后径向磁轴承轴套表面的频率响应曲线如图9所示。由图9可知，振动响应幅值在(300-1 300)Hz范围内较大，与固有频率的分布区域一致。在2 700 Hz处，有峰值，对应转速为5 100 rad/s，已超出飞轮电池工作转速，不会出现不稳定问题。激励频率和固有频率相同时，系统会发生共振，转子表面，电机转子表面和前、后磁轴承轴套表面有最大振动幅值。这与模态分析的前两阶固有频率基本吻合，验证了模态分析的有效性。

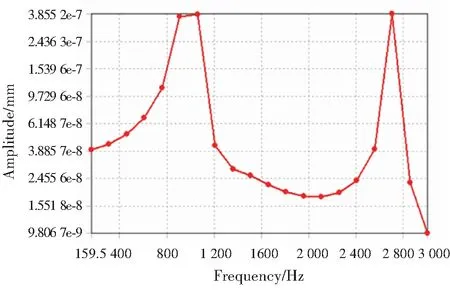
(a) 转子表面

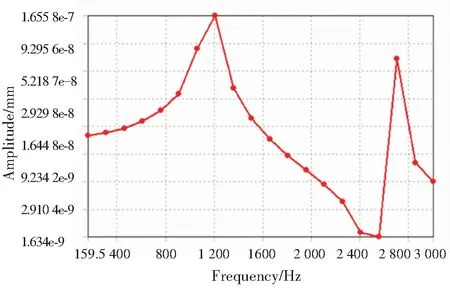
(b) 电机转子表面

(c) 前轴套表面

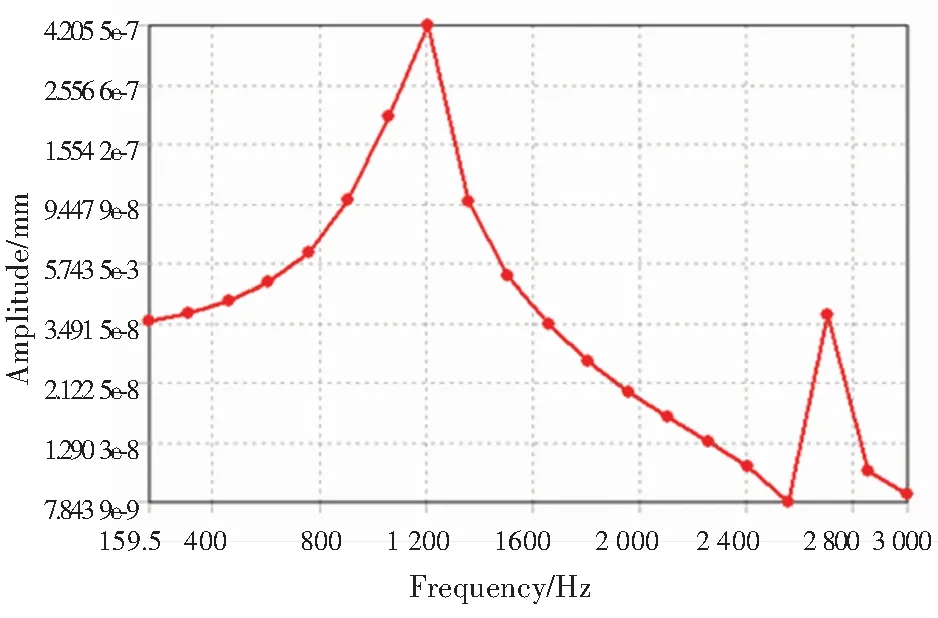
(d) 后轴套表面

4 结构优化设计

飞轮电池正常工作时会跨越临界转速区间，有强烈振动现象。本文采用优化转子外环和轮毂结构参数的方法，增大转子的临界转速数值，以此来提高飞轮电池的最大储能密度。以降低转子表面振动幅值为目标，对转子外环的宽度和高度，轮毂的宽度和半径以及转子转动角速度进行耦合分析。

本文以降低转子表面最大变形量为目标，在Workbench中使用响应曲面优化分析工具，对转子外环的宽度和高度，轮毂的宽度和半径进行优化设计。设定飞轮电池转子系统转速、转子外环的宽度和高度，轮毂的宽度和半径为输入变量，转子表面最大变形量和转轴等效应力为输出变量。外加载荷和约束与模态分析部分相同，如图10所示。

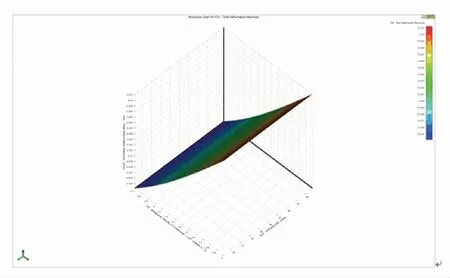
(a) 转子外环宽度

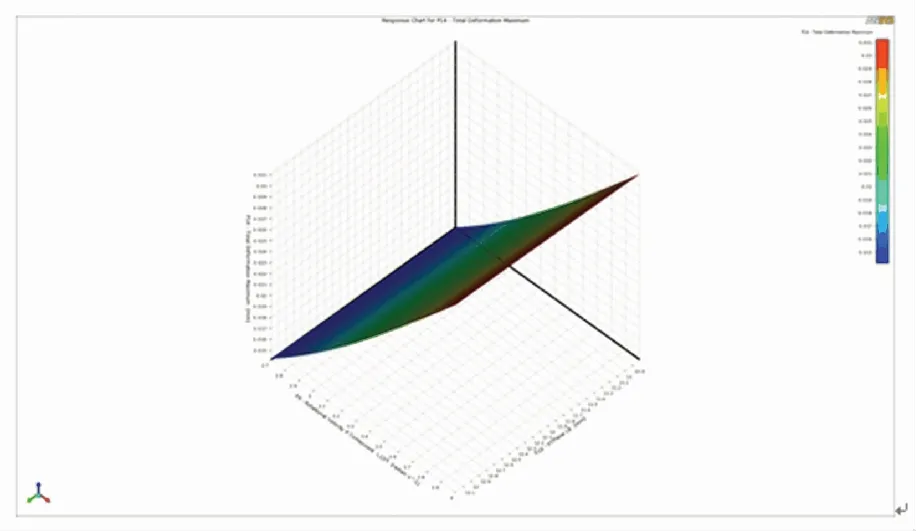
(c) 轮毂宽度

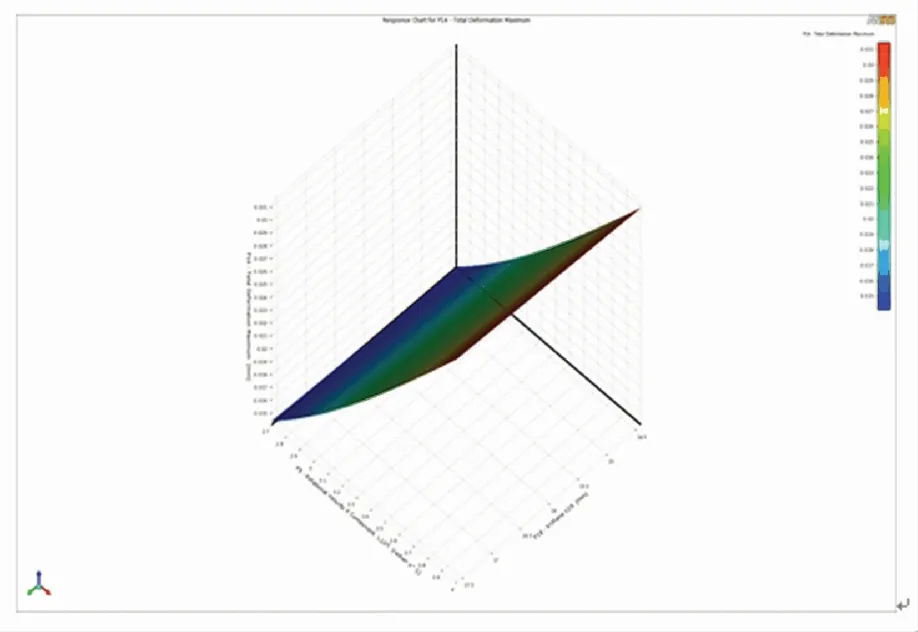
(b) 转子外环高度

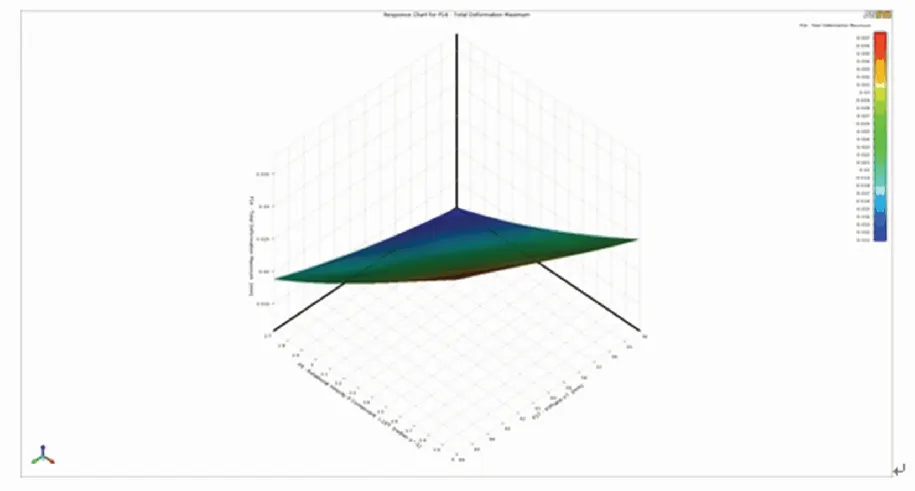
(d) 轮毂半径

由图10(a)可知，增加转子的转速，转子表面最大变形量逐渐增大。相同转速下，增大转子外环宽度，转子表面最大变形量先减小后增大。外环宽度为49.2 mm时，有最小值；由图10(b)可知，转子外环高度时相同，增加转子系统转速，转子表面最大变形量同样会不断增加。增加转子外环高度，转子表面最大变形量也是不断增大的；由图10(c)可知，增加转子转动角速度，转子表面最大变形量不断增大。相同转速下，轮毂宽度不断增大，转子表面的最大变形量呈现先减小后增大的趋势。轮毂宽度为11.4 mm时，转子表面最大变形量有最小值；由图10(d)可知，增大转子转速，转子表面最大变形量同样不断增大。相同转速时，轮毂半径与转子表面的最大变形量呈正相关关系。

转轴最大等效应力与转子外环、轮毂关系如图11所示。由图11(a)可知，增大转子外环宽度，转轴最大等效应力不断增大。外环宽度为49.2 mm时，转轴的最大等效应力为89.78 MPa，小于合金钢许用应力。由图11(b)可知，随着外环高度的增大，转轴最大等效应力呈现先增大后减小再增大的趋势。外环高度为16 mm时，转轴最大等效应力有最小值，为89.7 MPa。由图11(c)，增大轮毂宽度，转轴最大等效应力先增大后减小再增大。轮毂宽度为11.4 mm时，转轴的最大等效应力为93 MPa，小于合金钢许用应力。图11(d)与图11(a)类似，轮毂半径与转轴最大等效应力呈正相关关系。

(a) 转子外环宽度

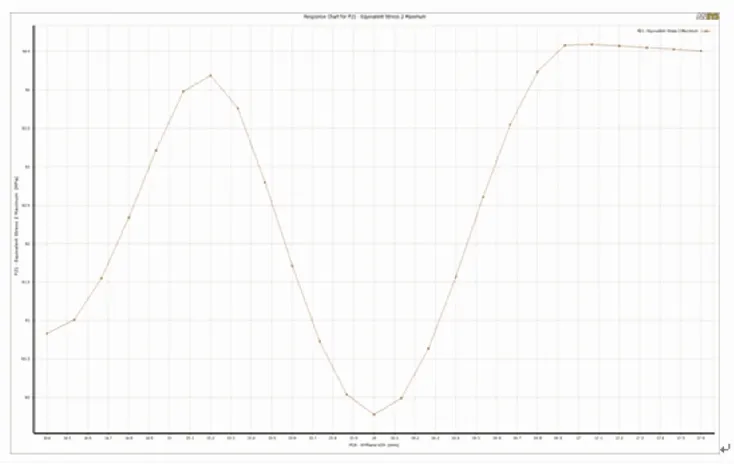
(b) 转子外环高度

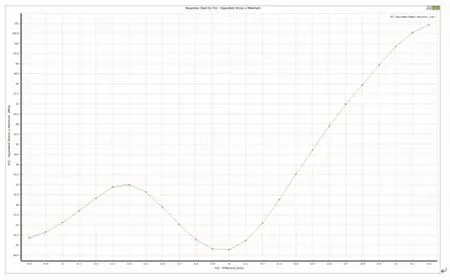
(c) 轮毂宽度

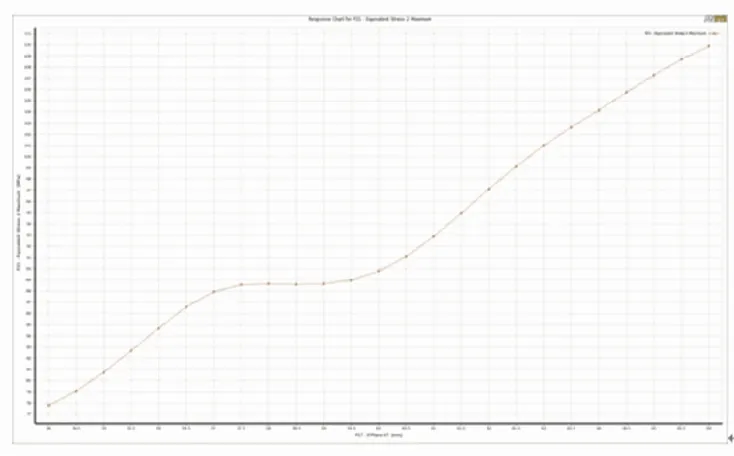
(d) 轮毂半径

综合考虑转子表面最大变形量、转轴最大等效应力与转子结构的关系和飞轮电池设计要求，在Workbench软件的DM模块，重新设定转子外环和轮毂的结构参数。其中，转子外环宽度为49.2 mm，转子外环高度为16 mm，轮毂宽度为11.4 mm，轮毂半径为62 mm。模态分析得到飞轮电池转子系统的坎贝尔图，如图12所示。由图12可知，一阶临界转速为2 627 rad/s，二阶临界转速为4 113 rad/s。相比结构优化之前，飞轮电池转子系统的二阶临界转速有了较大提升。根据储能密度公式，优化飞轮电池转子外环和轮毂结构后，提高了飞轮电池的储能密度。

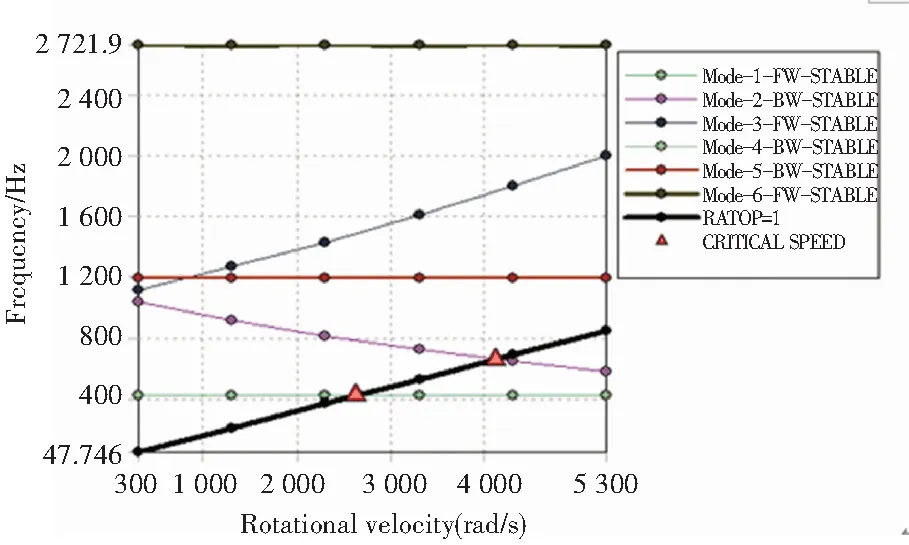
图12 坎贝尔图

5 结束语

本文使用Workbench软件通过模态分析、谐响应分析和响应曲面优化设计仿真分析了飞轮电池磁悬浮转子的动力学行为。仿真结果表明，转子系统临界转速位于工作转速区间内，会产生强烈共振现象。不平衡力作用时，转子系统不稳定性加剧，飞轮电池转子表面变形较大。采用直接优化方法，优化了转子外环和轮毂结构。仿真结果表明，尺寸改进后，飞轮电池转子系统的临界转速显著提高，提高了飞轮电池的最大储能密度。