基于大数据的大学生兴趣爱好特征聚类研究

贺 奇， 董延华， 宋嘉怡， 王 瑜

(吉林师范大学 计算机学院， 吉林 四平 136000)

0 引 言

信息技术普及与推广，直接影响各个领域的发展，特别是在社交网络领域中，越来越多的大学生群体选择在社交网络分享生活日常和兴趣爱好。在教育学中，Klassen等研究者强调兴趣爱好在个体追求知识和追求进步的过程中可以起到巨大的推动力[1]。而在计算机中，研究并分析兴趣爱好特征也有了长足的应用前景。本文首先收集一份从社交网络平台抽取的描述大学生基本信息和兴趣爱好的数据集，并对数据集进行预处理；其次，通过大数据分析的方法及原理，利用k-Means算法划分出五类大学生群体；最后，分析每一个群体所代表的兴趣爱好特征。

1 k-means聚类

k-means聚类算法即K均值算法是由MacQueen提出的，是一种无监督学习，同时也是基于划分的聚类算法[2]。k-means算法的基本思想：首先随机选取k个样本作为初始聚类中心，计算剩余的每个样本到初始聚类中心的欧氏距离，分别将其分配给与其最相似的聚类；其次，利用迭代的方法更新聚类中心的值，不断重复这一过程直到聚类中心不再变化。k-means算法的流程图如图1所示。该算法具有简单、快速、容易理解和效果好的优点，主要基于最小距离来划分样本对象，很适合本文的数据集。

2 分析过程

2.1 采集数据

为了让实验结果更加完整和精确，数据均匀采样2016年到2019年的大学一年级、二年级、三年级和四年级的社交网络信息。为了让实验结果更加丰富，每个样本都包含40个变量，例如gradyear,gender,age,friends这4个变量分别代表毕业年份、性别、年龄和好友数等基本信息。还有其余36个变量代表36个词语，这36个词语代表五大兴趣类：课外活动、时尚、宗教、浪漫和反社会行为。变量的大小取决于对应词语在社交网络平台中的频率和次数。最终收集了一份包含三万个样本的大学生社交网络信息数据集。

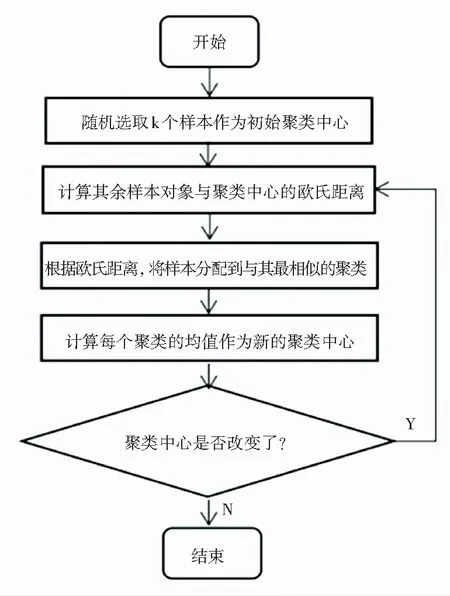
图1 k-means算法流程图

2.2 数据探索和预处理

性别变量和年龄变量中都存在缺失值，k-means无法直接处理，因此在构建模型之前，需要对缺失值进行处理，处理的方法有两种方案，一是删除，二是以某种方法填补。对于性别变量，利用pandas中的函数可以完成。而对于连续型变量年龄，在填补之前需要统计非缺失值的数量，从而能够计算缺失值数量。实验得出有2 724个样本(约9%)缺少性别数据，5 086个样本(约17%)缺少年龄数据。进一步观察年龄变量的描述性统计发现，最大值为106.927，最小值为3.086，显然有异常值。因为本文的样本是大学生样本，所以该最小值和最大值似乎不可信，因为现实中不太可能会有一个3岁或者106岁的人就读大学。这种异常数据往往会影响最终的建模分析结果，因此需要进行异常值处理。大学生的合理年龄区间为13～24岁，因此对于数据集，如果年龄在13～24岁之外，将其标记为空值。

(1)通过虚拟编码处理分类变量的缺失值。对于样本中的缺失值，其中一种方案是删除带有缺失值的样本。而数据的40个变量中只有二个变量存在缺失值，缺失值在数据中整体不多，直接删除缺失值会使数据变少，且直接删除往往会导致失去很多的可用数据。对于性别这种分类变量，缺失值的样本跟其他样本的差别明显，可以为性别变量增加一个单独的分类，将空值替换为“不清楚”。

由于k-means聚类算法需要计算样本之间的距离，还需要对分类变量虚拟编码(也称为OneHot编码)。虚拟编码将一个有K个取值的分类变量转换成K个二元变量。利用虚拟编码将性别变量转换成男生、女生和不清楚3个变量。这3个变量取值为0或1，分别代表某一大学生是否是某一性别类型。对于一个样本，在这3个变量下同时只能一个变量取值为1，其他变量取值为0。

(2)通过填补方法来处理数值变量的缺失值。与性别这种分类变量不同，对于年龄这种数值变量的缺失值，可以用一个特殊的值对缺失值进行填补，常用的填补值包括给定值、均值、中位数等。在本文中，使用的是最具代表性的均值填补法。均值的计算在默认情况下是无法对包含缺失值的数据计算均值的。通过给均值函数传入额外的参数，计算均值为17.252 428 851 574 9，在实验中对年龄数值变量保留三位小数，从而样本中年龄缺失值被正确填补为均值17.252。

(3)数据标准化。数据的标准化是很多多元统计方法必要的前期工作，如综合评价、聚类分析等。数据标准化的方法很多，用不同的标准化方法得到不同的结果，从而影响了对实际问题合理客观地认识和判断[3]。K-means聚类算法需要计算样本的距离，在构建模型之前，需要进行数据标准化。常用的方法有min-max标准化和Z-score标准化等。Z-score标准化又称标准差标准化，归一后的数据呈正态分布，即均值为零，如公式(1)：

(1)

其中，μ为所有样本数据的均值，如公式(2)；σ为所有样本数据的标准差，如公式(3)。Z-Score标准化算法简单方便，结果方便比较，不受数据量级的影响。因此在本文中直接采用Z-score标准化方法。

(2)

(3)

2.3 模型训练

Sklearn是scikit-learn的简写，sklearn是一个Python专用于机器学习的经典模块库，能够实现各种学习模型的算法，包含了数据预处理到模型训练的许多方面。为了将大学生社交网络信息数据进行聚类，使用sklearn中的KMeans类 。其中一个重要参数就是聚类数目，在本文中将聚类的个数设置为5。

3 聚类结果分析

聚类结果的定量性能评价指标有互信息、同质性和完备性等，但是这些指标并不能指示聚类结果是否达到本预期分析目标。本文分析目标是确定具有相似特质和兴趣爱好的大学生的分类。因此，很大程度上，需要的不是定量的评价指标结果，而是定性地对聚类结果进行分析。观察5个类别中每一个类的样本数目，如图2所示。

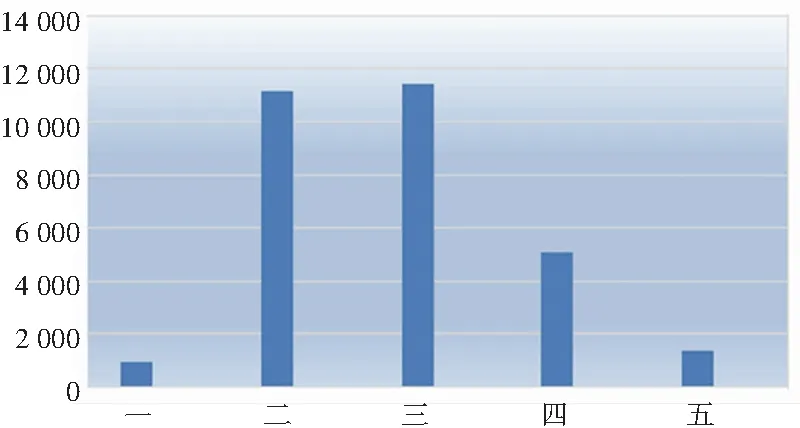
图2 聚类数目

在聚类的五个类中，最大的类中有11 441名大学生，最小的类中有969名大学生。需要注意的是，因为k-means聚类会随机选取初始的聚类中心，因此每次运行的结果可能也会不同。为了更好地理解每一个类所代表的大学生群体的特点，观察每一个类的聚类中心，聚类中心结果保存在聚类模型的中心点属性中。

因为数据已经使用Z-score方法标准化，可以直接通过观察聚类中心在每一个变量上的取值情况来分析每一个聚类中心的含义。如果聚类中心在某一个变量取值大于0，代表该聚类所代表的群体在该变量取值大于群体平均水平。首先，对上述聚类结果数据进行转置；其次，对每一个聚类中心的变量取值从大到小排序。通过观察每个聚类前6个变量来分析聚类所代表的群体，获得5种聚类，聚类结果见表1。

(1)聚类1占总数的3%，其中“时尚品牌”和“潮流品牌”2个变量取值大于3，“购物”变量取值大于1，说明这部分大学生比较关注时尚潮流，购物消费比较高,注重物质消费。第一个聚类所代表的大学生群体特点为爱好购物，追崇时尚，关注潮流服饰。

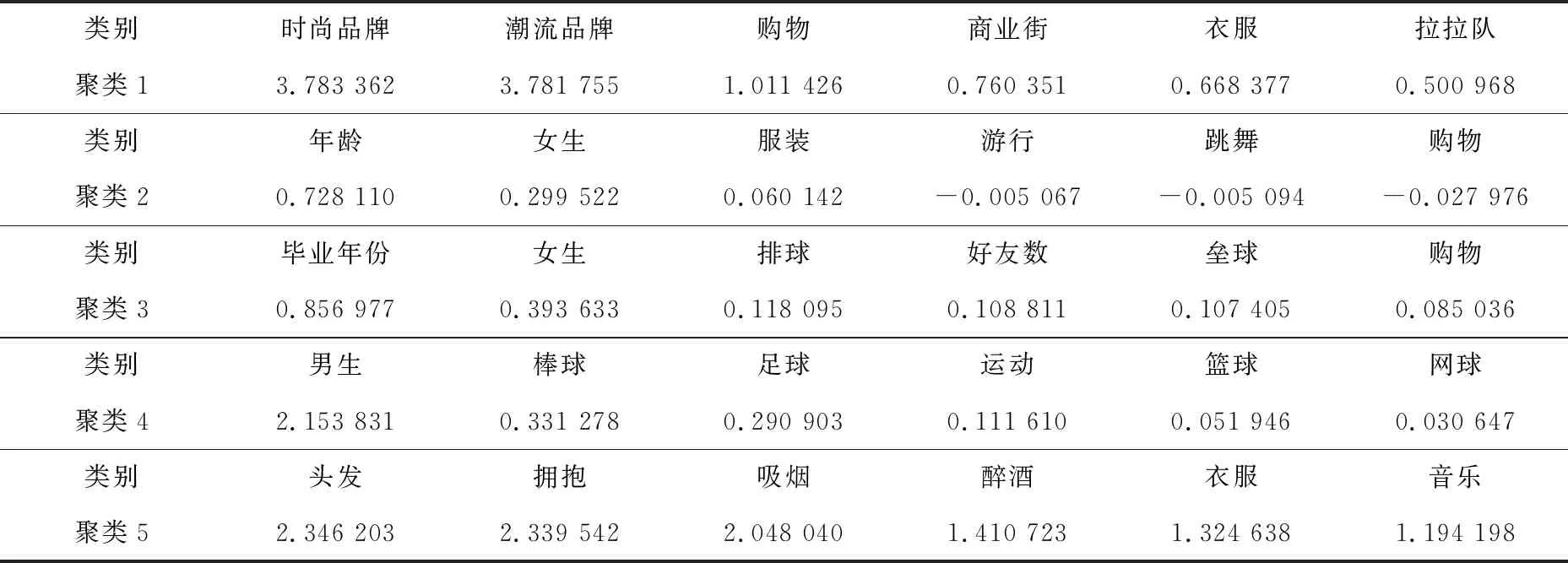
表1 聚类结果分类表

(2)聚类2占总数的37%，其中“年龄”、“女生”和“服装”等变量取值都大于0，第二个聚类所代表的大学生群体的特点为女生占大多数，大部分变量取值为负，这一类人群可能对应社交平台资料不全，且很少发布内容的群体。

(3)聚类3占总数的38%，其中“毕业年份”、“女生”、“排球”、“好友数”、“垒球”、“购物”、还有“火辣”、“商业街”和“英式足球”等变量取值都大于0，说明这部分大学生女生所占比例高。第3个聚类所代表的大学生群体的特点是爱好购物，爱好体育运动，女生居多。

(4)聚类4占总数的17%，其中“男生”变量取值远远大于0，显然男生居多。“棒球”、“足球”、“运动”、“篮球”、“网球”等变量取值都大于0，说明相对于女生来说，男生更热爱体育运动。第4个聚类所代表的大学生群体的特点是喜欢体育运动，大多为高年级男生。

(5)聚类5占总数的5%，其中“头发”、“拥抱”、“吸烟”变量都为大于2，“衣服”、“醉酒”、“音乐”、“摇滚”等变量取值都大于1，说明这部分大学生追求个性，注重外表，有自己的爱好。第5个聚类所代表的大学生群体的特点是喜欢浪漫，爱好音乐，有酗酒的习惯。

4 结束语

本文借助大数据平台对大学生社交网络信息进行聚类分析，利用k-means算法对具有相似特质和兴趣爱好的大学生进行了分类，获得五类大学生群体,并对每一个群体所代表的兴趣爱好做了特征分析，实现了数据挖掘的效果。相关学校可以通过聚类结果，探究大学生群体用户的兴趣关注点，分析兴趣爱好信息，有效地支持大学生的个性分析、行为分析和心理分析。