外接球求解的一招二式

赵钧锐

(河南省民权县高级中学高二29班 476800)

有关多面体外接球的问题在高考试题中屡见不鲜,而问题实质就是求球半径R或确定球心O的位置问题.本文通过近年来积累的部分试题中外接球的问题,谈外接球求解的一招二式.

一、一招——嵌于长方体

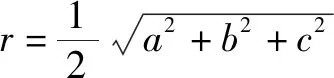
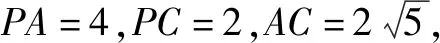
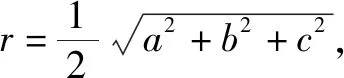
二、二式之一——小圆法

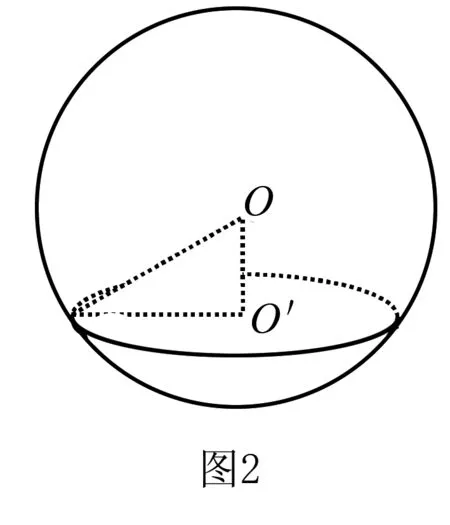
众所周知，圆有垂径定理，而球亦有类似性质，如图，利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质,确定球心位置.此法是运用OO′⊥⊙O′,而⊙O′是球的小圆，所以称此法为小圆法.

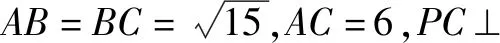
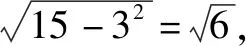
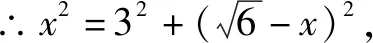
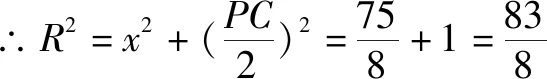
故选D．

评注利用解小圆法求几何体外接球的半径，是一种明了、行之有效的方法，解题的第一件事就是要找到球心O的位置.要找球心O的位置，没有固定的规律，要结合几何体的特征，发挥自己的空间想象力分析.找到球心O的位置后，再确定底面圆的圆心D位置，如何表示出球心O到截面圆圆心D的距离，这个是难点，要结合几何图形分析.

三、二式之二——坐标法

对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为O(x,y,z) ，利用球心到各顶点的距离相等建立方程组，解出球心坐标，从而得到球的半径长. 坐标的引入，使外接球问题的求解从烦琐的定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度.

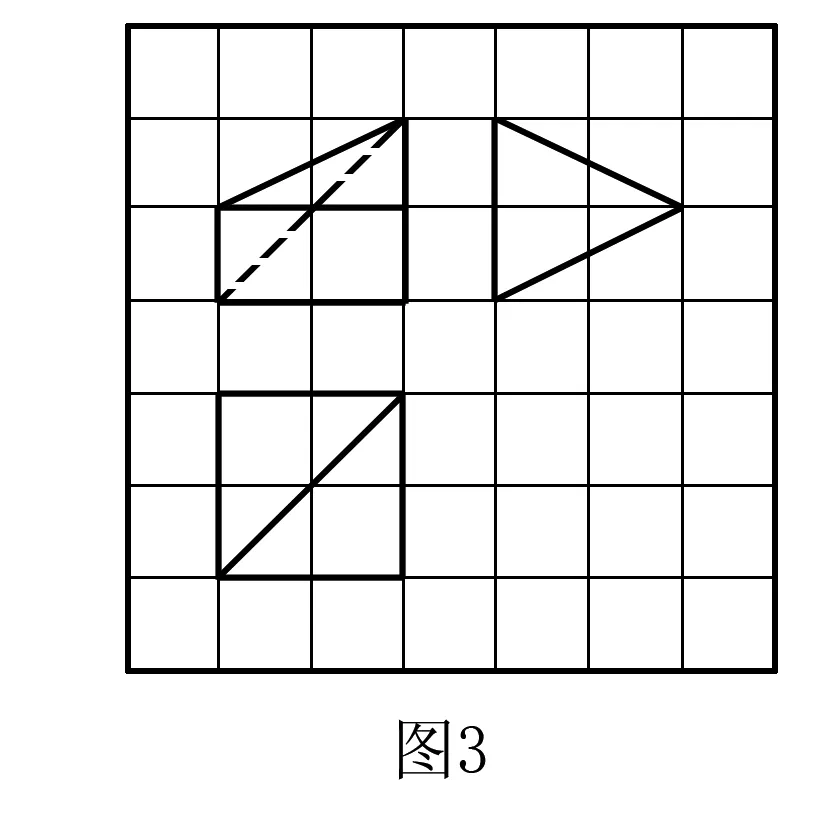
例3 如图小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为( ).

解由三视图可知，该几何体为如图4所示的四棱锥S-ABCD，其中四边形ABCD为矩形.

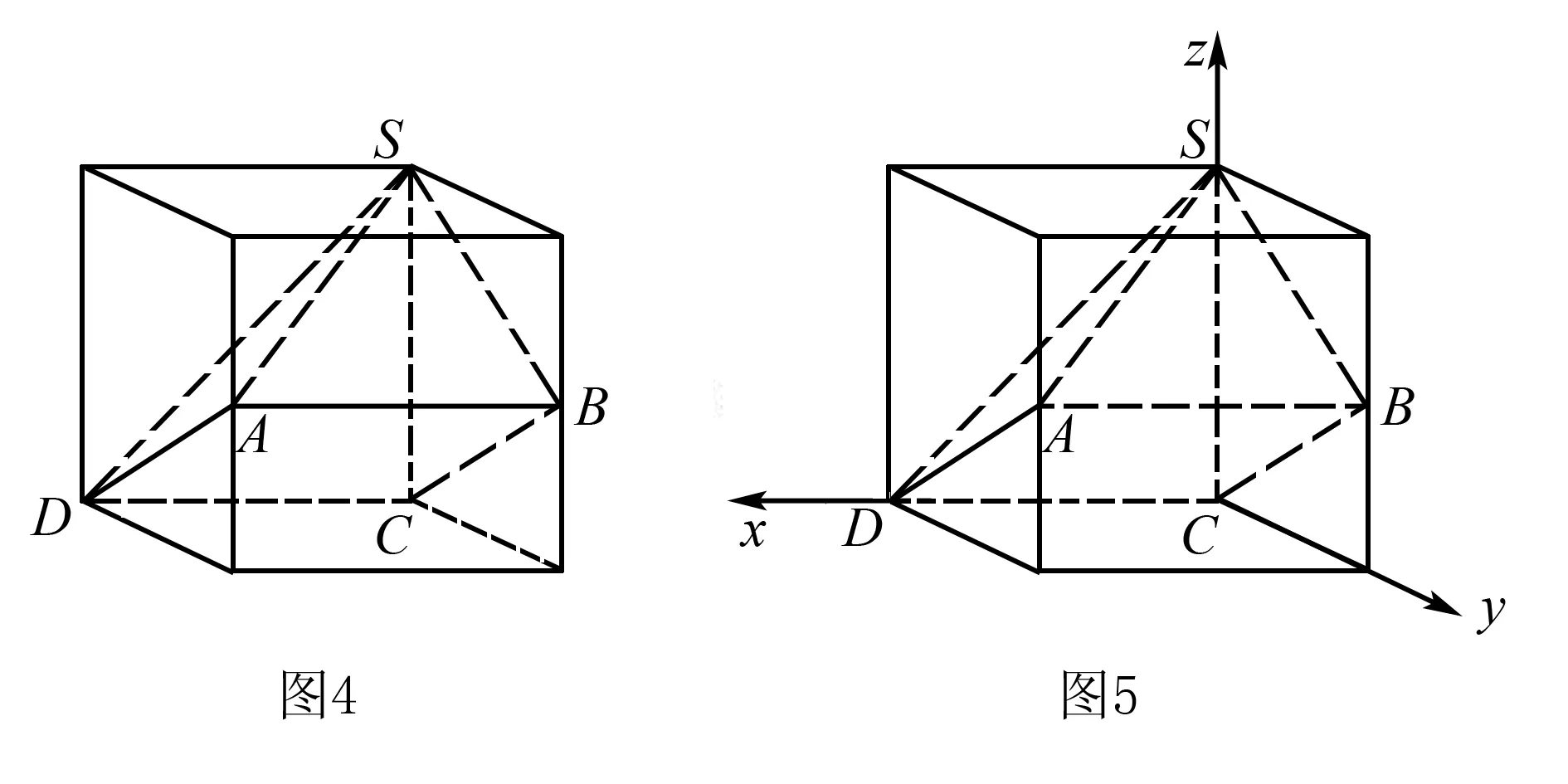
如图5，建立空间直角坐标系，则A(2,2,1),B(0,2,1),S(0,0,2).设球心O的坐标为(x,y,z)，则OS=OA,OS=OB,OS=OC,得到方程组

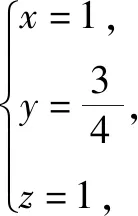
故选C．

评注由这个例子可以看出，对于规则和不规则的几何体外接球问题，通过设球心坐标解方程组的方法，不仅可以确定球心位置，也可以确定球半径，大大降低了思维难度，提高了做题的准确性.