回采工作面中间巷围岩稳定性研究

袁 芳 ，牟宗龙 ，杨 景 ，曹京龙 ，杨博飞

（1.中国矿业大学 江苏省矿山地震监测工程实验室，江苏 徐州 221116；2.中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州 221116；3.中国矿业大学 矿业工程学院，江苏 徐州 221116）

近年来，国内外学者分别从理论、数值及工程等方面研究了采空区边缘侧向应力场的分布特征[1-5]；且针对工作面前方煤岩层应力分布研究取得了丰富的成果[6-7]。而中间巷与工作面上下两巷成一定角度的布置方式导致其周围煤岩体在受到掘巷及重复采动影响时，应力场呈现出不同的分布特征[8]。文献[9]根据现场监测的巷道围岩变形量，分析了中间巷的受力及应力分布特征，认为中间巷与工作面上下两巷交叉点前后40 m 范围内三角区尖端及巷帮是加强支护的重点，但是观点缺乏足够的理论支承。文献[10]采用应变软化模型，分析了中间巷与工作面上下两巷相交段的围岩稳定性，认为中间巷不同程度的变形受到巷道角度的影响。多位学者分别针对不同矿井条件提出了工作面过中间巷的具体措施[11-14]，但是很少有学者从中间巷的层位优化研究中间巷的采动应力分布特点。中间巷作为辅运的关键巷道，通常在回采工作面前方开掘，但是随着工作面的回采，超前应力集中影响范围接近中间巷，易诱发巷道冒顶、冲击矿压等灾害[15-18]。因此研究中间巷合理的布置方式以及采动应力分布对于矿井特殊时期的安全高效生产具有重要意义。为此以中间巷为研究对象，考虑采动影响下，采用数值模拟与理论分析相结合的方式，对 9 种不同中间巷的围岩应力、位移和塑性区分布进行模拟和分析，探讨不同条件下中间巷以及工作面围岩变形规律，为中间巷的巷道设计提供理论参考依据，并提出适合深部矿井安全开采的合理的中间巷布置方式。

1 中间巷应力场力学分析

文献[19]提出的“内外应力场”理论，比较正确的反映了工作面侧向应力场的分布特征；文献[20]基于该理论建立了深部沿空巷道侧向应力场分布的工程力学模型。随着中间巷以及两侧煤巷的掘进，中间巷掘进影响区煤岩体应力重新分布，建立的中间巷侧向应力场模型如图1。

图1 中间巷侧向应力场力学模型Fig.1 Mechanical model of lateral stress field of middle roadway

由矿压分布规律[20]：

式中：h 为采高；H2为低位岩层厚度

式中：H 为采深；H1为高位岩层厚度。

式中：K1、K2为巷道帮部峰值应力集中系数。

在深部条件下，高位岩层形成的“外应力场”远大于“内应力场”，因此，由低位岩层在工作面形成的“内应力场”可忽略不计。

对中间巷应力场力学模型做如下简化：以采空区煤壁为坐标原点O，以煤层垂直方向为纵轴，以煤层上方顶板一点与采空区煤壁的水平距离为横轴，建立中间巷应力场直角坐标系，如图1。其中A、C、E分别为上覆岩层作用在煤岩体上不同位置处的应力峰值，假设掘巷后沿空巷道及中间巷顶板上方垂直应力下降为 nρgH（n 为应力折减系数，n≤1），将掘巷后中间巷煤岩体侧向应力分布曲线简化为分段函数。

图中 OA 段斜率为 K2ρgH/x1，则 σi= K2ρgHx/x1，同理，得出中间巷侧向应力场分段函数：

x1、x2、x3、x4、x5、x6分别表示：

式中：K1、K2、K3为巷道帮部峰值应力集中系数；a、b 分别为中间巷和沿空巷道宽度；c 为中间巷帮部峰值应力与原岩应力处的距离；l1为中间巷帮部峰值应力距离巷壁的距离；l2为中间巷与沿空巷道所夹煤体宽度；l3为保护煤柱宽度；ρ 为上覆岩层密度。

由式（4）、式（6）可知，在深部条件下，忽略 K2及n 得：

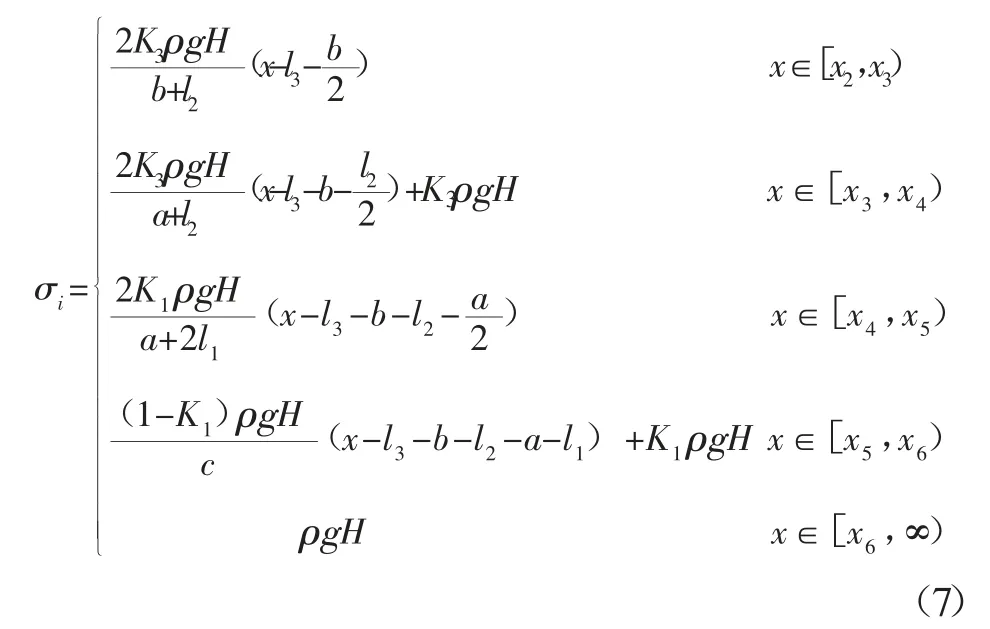
在实际开采中，还需要考虑工作面受采动应力kρgH 的影响，k 为动载系数，与工作面的地质条件和开采技术条件等因素有关，因此，中间巷周围煤岩体在回采期间的总支承压力为：

通常情况下，a、b、l3确定时，工作面支承压力分布 σ 与 l2的关系如下：当 x∈[x2,x3）∪[x4,x6)时，l2的宽度与 σ 成反比；当 x∈[x3,x4）时，l2的宽度与 σ 无法判断；当 x∈[x6,∞）时，l2的宽度与 σ 无关；同一工作面，中间巷与沿空巷道所夹煤体宽度l2随着中间巷与沿空巷道的夹角变化而变化；锐角时，角度越大，l2的变化速率越快，支承压力 σ 越大，至 90°时达到最大值；钝角时，支承压力随着角度的增大而减小。根据l2与工作面支承压力的关系，有必要从多个角度对中间巷工作面进行模拟研究。

2 数值模拟

中间巷采动应力分布受巷道自身的方位影响较大[21]。基于中间巷与工作面上、下两巷的位置关系，运用FLAC3D数值模拟分析软件多个θ 角度对中间巷进行研究，中间巷示意图如图2。中间巷工作面为分步开挖工作面，工作面宽度为250 m，采高6 m，该工作面一侧为实体煤，另一侧为采空区；采用更改强度参数的弹塑性求解法生成初始地应力场[22]。

分别模拟 40°、45°、60°、75°、90°、105°、120°、135°、150° 9 种不同夹角的中间巷，考虑边界效应，模型长×宽×高取800 m× 750 m× 236 m，模型底部及四周为固定边界，顶部为自由应力边界（模型顶部施加上覆岩层自重应力17.5 MPa），初始应力场按自重应力场考虑，数值模型如图3，物理力学参数见表1[23]；考虑到超前支承压力影响范围以及上区段采空区对中间巷工作面的影响，所以在开挖中间巷工作面之前，首先开挖上区段采空区，如图3。当工作面距离中间巷100 m 之前每50 m 开挖1 次，100 m 之后每 20 m 开挖 1 次。

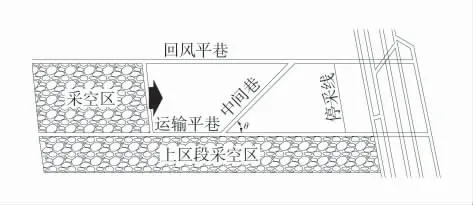
图2 中间巷示意图Fig.2 Diagram of middle lane

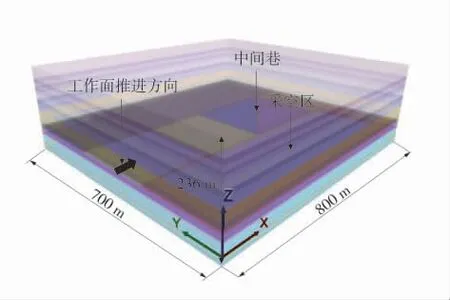
图3 中间巷FLAC3D 模型Fig.3 FLAC3D model of middle lane

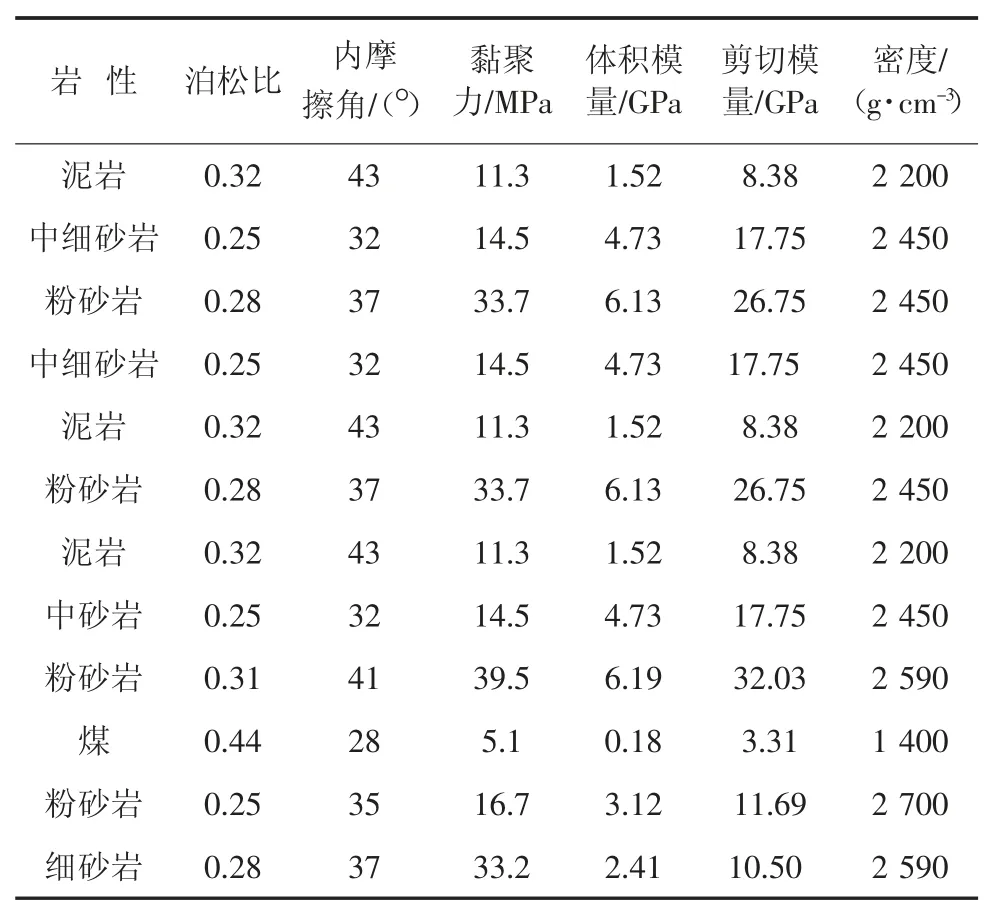
表1 岩层物理力学参数Table 1 Physical and mechanical parameters of rock strata

模拟得出煤层垂直应力为22.08 MPa，文献[24]采用水压致裂法在该地质条件下进行地应力测量，得出该地质条件下垂直应力均值为20.67 MPa；文献[25]运用钻孔套心应力解除法测得出垂直应力为23.89 MPa；2 种地应力测量方法得出的结果与数值模拟结果较为一致，证明了数值模拟结果的可靠性。

3 数值模拟结果分析

3.1 中间巷帮部垂直应力分布特征

根据中间巷与沿空巷道夹角的大小，中间巷可分为锐角中间巷（夹角小于或等于90°）和钝角中间巷（夹角大于90°）。工作面距离中间巷0 m，即中间巷处于最危险状态下巷道帮部垂直应力分布曲线如图4 和图5，曲线左侧为中间巷靠近采空区侧。

图4 锐角中间巷帮部垂直应力分布Fig.4 Vertical stress distribution of middle roadway at an acute angle

图5 钝角中间巷帮部垂直应力分布Fig.5 Vertical stress distribution of middle roadway edge at obtuse angle

锐角中间巷帮部垂直应力值和应力峰值随巷道角度的增加而增大，且各角度中间巷应力峰值位置位于沿中间巷倾向方向 15 m 处，其中，40°、45°、60°、75°、90°中间巷帮部峰值应力集中系数分别为：2.79、2.55、2.83、3.12、3.17。由于中间巷角度以及长度的变化，也就是说工作面的采动对中间巷的影响范围随着中间巷角度的增加而增大，导致了中间巷帮部应力值的差异。从图中可以看出，45°中间巷帮部垂直应力值和应力峰值均低于其他角度，而90°则相反。

钝角中间巷的帮部垂直应力分布特征与锐角中间巷相反，应力值随巷道角度的增加而减小，如图5，钝角中间巷垂直应力曲线呈两端高、中间低的“凹”型特征。帮部应力峰值位于中间巷倾斜方向10～15 m 处，各角度峰值应力集中系数分别为：2.97、2.68、2.26、2.51，与锐角中间巷 45°垂直应力相对应，135°中间巷同样低于其它角度，且135°峰值应力集中系数小于45°。因此，仅从中间巷帮部垂直应力的角度考虑，中间巷布置的合理角度应为135°。数值模拟中间巷帮部垂直应力变化规律与理论研究结论基本一致。

3.2 中间巷顶底板位移响应特征

巷道围岩变形量是反映巷道破坏程度和确定中间巷角度合理性的重要指标。40°～105°中间巷在不同的开挖步数下巷道顶底板变形量（x 负轴代表顶板，正轴代表底板，下同）如图6。

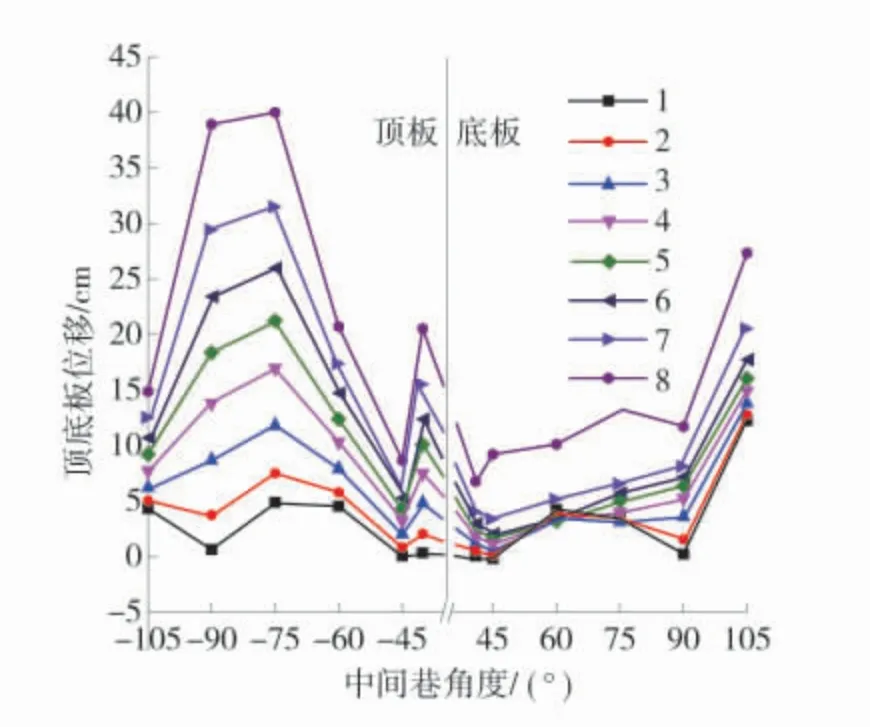
图6 中间巷顶底板位移响应曲线Fig.6 Displacement response curves of middle roadway roof and floor

从图6 中可看出，中间巷底板总变形量在相同进尺下随着角度的增加而增大；而顶板总变形量随着角度的增加先增大后减小，且90°、75°顶板变形量较大，说明对中间巷角度变化最敏感的是巷道顶板。各角度中间巷顶底板变形量范围为0.13～40.13cm，而45°中间巷巷道顶底板在不同开挖步数下的变形量为 2.3～8.8 cm，小于其它角度。因此，中间巷为45°时，顶底板变形量较小，中间巷角度较为合理。

120 °～150°巷道顶底板位移变化量如图7，曲线1～11 分别代表工作面的不同进尺。不同角度中间巷顶底板变形量为 3.32～27.69 cm，最大变形量约为45°时的 3 倍左右，所以，对比 120°～150° 中间巷顶底板变形量，中间巷布置的合理角度同样应为45°。

图7 中间巷顶底板位移响应曲线Fig.7 Displacement response curves of middle roadway roof and floor

3.3 中间巷煤岩体塑性区分布规律

塑性区是工作面回采过程中煤岩体发生塑性破坏的直观显示，塑性区形态决定了煤岩体的破坏形式及破坏程度[26,-27]，各角度中间巷历史塑性区体积分布如图8 和图9。

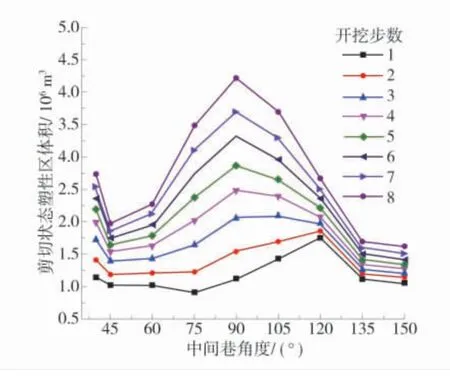
图8 历史剪切状态塑性区体积分布Fig.8 Volume distribution in plastic zone of historical shear state

图9 历史拉伸状态塑性区体积分布Fig.9 Volume distribution in plastic zone under historical tensile state

由图8 和图9 可知：不同角度中间巷塑性区体积都在最后一步达到最大值，且拉伸状态塑性区体积大于剪切状态塑性区体积，历史剪切和拉伸状态塑性区体积分别为 0.9×106～4.2×106m3、2.4×106～7.3×106m3。2 种不同破坏状态的塑性区体积在 45°、135°、150°时塑性区体积小，应力集中范围小，有利于巷道维护。锐角中间巷45°角在既有工况产生的剪切、拉伸塑性区体积为 2.0×106m3、4.0×106m3；钝角中间巷150°角在该条件下产生的剪切、拉伸塑性区体积为 1.6×106m3、3.7×106m3，对比 2 种不同类型的中间巷塑性区体积可知，150°中间巷为最优角度。

4 中间巷方案优化

中间巷角度方案优化示意图如图10。

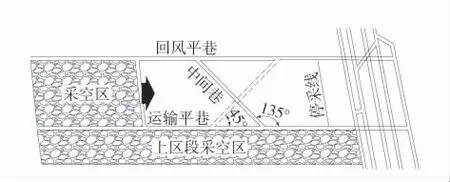
图10 中间巷角度方案优化Fig.10 Optimization of angle scheme in middle lane

根据数值模拟结果，中间巷在45°角时巷道顶底板变形量最小；在135°时帮部峰值应力集中系数最小，150°中间巷在已有工况下产生的剪切、拉伸塑性区体积最小，但是与 135°相比仅相差 0.02×106m3、0.1×106m3，差值较小，同时考虑到中间巷长度的合理性，实际应选择135°。现场实际及数值模拟研究结果均表明，中间巷靠近采空区一侧煤岩体应力高，巷道变形量大，中间巷与沿空巷道的夹角为135°时，如图10，随着工作面推采，首先受到超前支承压力影响的是靠近回风巷的部分中间巷，该部分中间巷周围煤岩体远离采空区，受采空区影响较小，工作面向前推进，超前支承压力影响范围逐渐靠近采空区侧中间巷，但中间巷受采空区影响范围也不断减小。而45°中间巷则相反，巷道交叉部分在承载采空区悬顶结构的同时受工作面采动的叠加影响，且叠加范围较大，巷道及周围煤岩体难以有效控制，导致该角度下巷道容易发生失稳。因此，中间巷应以钝角范围为优选角度，且在135°时为最优角度。

5 结 论

1）中间巷与沿空巷道所夹煤体宽度l2随着中间巷与沿空巷道的夹角变化而变化；锐角时，角度越大，l2的变化速率越快，支承压力 σ 越大，至 90°时达到最大值；钝角时，支承压力随着角度的增大而减小。

2）不同角度中间巷帮部垂直应力峰值位于中间巷倾向方向10～15 m 处，峰值应力集中系数介于2.26～3.17 之间，其中 135° 峰值应力集中系数为2.26，为最小值。而45° 中间巷顶底板在不同开挖步数下变形量最小。模拟塑性区结果显示，工作面以剪切破坏为主，更大范围的采空区以拉伸破坏为主。对比在已有工况下产生的剪切、拉伸塑性区体积发现，150° 中间巷最小，但是与 135° 相比差值较小，考虑到中间巷长度的影响，应选择 135° 。

3）随着工作面推采，135° 中间巷首先受到采动影响的是靠近回风巷的部分中间巷，该部分中间巷周围煤岩体远离上区段采空区，影响小，工作面向前推进，中间巷受采空区影响范围不断减小。而45°中间巷则相反，巷道交叉部分在承载上区段采空区悬顶结构的同时受工作面采动影响。因此，中间巷应以钝角范围为优选角度，而且在135° 时为最优角度。