生日蛋糕里的“性价比”

卓西咔

从前几天开始，洛洛就频频盯着墙上的日历盼啊盼。明天就是洛洛的生日了，今天爸爸下班一进门，洛洛便从沙发上一跃而起。在爸爸的陪同下，洛洛来到蛋糕店为自己定制生日蛋糕。

一走进蛋糕店，他就被店里琳琅满目的糕点吸引了。在确定好定制的生日蛋糕的样式后，就要选择蛋糕的规格了。据店员介绍，洛洛选择的那款圆柱形的蛋糕，在同样的重量下，共有三种规格可供选择，分别是r ∶h=2∶1，r ∶h=1∶1 以及r∶h=1∶2，其中r为蛋糕的底面半径，h为蛋糕的高度。

“反正重量都一样，规格选哪个都差不多，爸爸你决定吧！”此刻的洛洛就像一只小馋虫，想吃上一口香软的蛋糕。

在了解了蛋糕的总费用（包括蛋糕的制作费用以及蛋糕的包装费用）后，爸爸笑着说道：“即便是重量相同，但规格不一样的话，费用是会有差别的。”

洛洛顿时摸不着头脑：“这是为什么呢？”

如何选出最省钱的蛋糕

★蛋糕的制作费用

假设蛋糕的总费用、制作费用和包装费用分别为P 、P1和 P2，则

P=P1+P2

若蛋糕的单价是60元/磅，据店员介绍，1磅（约为450克）的蛋糕的体积约为1800立方厘米，从而依据数量关系式得到

密度=质量

体积=450

1800=0.25（克/立方厘米）

蛋糕可视为一个圆柱体，其体积公式为

圆柱体积=底面积×高=πr2h

可进一步算出

P1=蛋糕单价×蛋糕重量=蛋糕单价×蛋糕密度×蛋糕体积=60

450×0.25×πr2h=1

30πr2h

★蛋糕外包装的费用

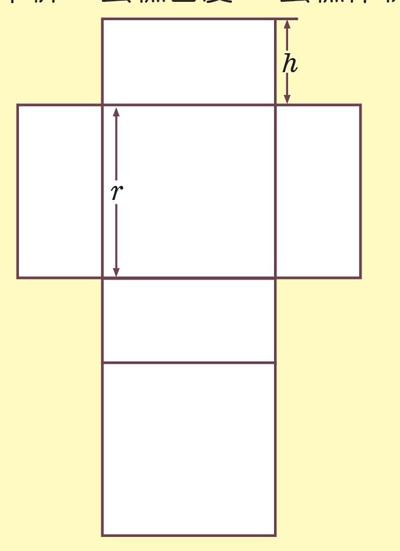
而包装费用方面，每平方厘米的包装盒需要0.05元。我们将立方体形状的包装盒展开（如右图所示），展开后的包装盒由4个长为r、宽为h的长方形以及2个边长为r的正方形组成，从而我们可以算出包装盒表面积为

S=2r2+4rh

所需的包装费用为

P2=包装盒单价×包装盒表面积=0.05×（2r2+4rh）=0.1r2+0.2rh

★蛋糕所需总费用

最后我们就能推导出总费用的表达式

P=P1+P2=1

30πr2h+0.1r2+0.2rh

现在爸爸想要定制一个1磅的蛋糕。

想知道到底哪种规格的蛋糕的总费用更低，只需分别将r ∶h=2∶1，r ∶h=1∶1 以及r ∶h=1∶2三种规格的數值代入上面的公式中，就可以通过计算得到，三种规格的蛋糕的总费用分别为：81.88元，80.67元和81.71元。

因而选择规格为r ∶h=1∶1 的生日蛋糕更省钱。

如何使蛋糕的派送费最少

★不同时间下的不同情况

洛洛这下明白了，原来相同重量的蛋糕所耗费的包装盒的面积未必相同，从而导致不同规格的蛋糕在包装费用上存在差异。选完蛋糕，接下来就是确定蛋糕的寄送时间了。洛洛的爸爸向店员要来了蛋糕寄送服务的价目表，一旁的洛洛也踮起脚尖围观表上的收费细则。

因受多种因素的影响，在不同时段送蛋糕所产生的成本会有所出入，因而不同时间段的寄送费用也会有所波动。比如，若在店内生意繁忙的时段送蛋糕，会导致店内人手不足，从而流失一部分订单，给店家造成损失;若在上下班的高峰期送蛋糕，则可能会因路上拥堵而使得店员在路上耽误更多的时间，等等。

★比一比，算一算

假设蛋糕预计送达的时间为x点，比如，x=6代表蛋糕需在上午6点送到顾客手上，x=19.5则代表蛋糕需在晚上7点半送到顾客手上，因为蛋糕店是24小时营业，所以有0≤x≤24。

设P*（x）为送蛋糕所需的费用，根据收费细则，有

P*（x）= x2-20x+125

在这一刻，爸爸和洛洛都不约而同地思考着这样一个问题——到底选在哪个时段送达，会使得费用最少呢？这次洛洛先说出了自己的见解。

假设a、b为两个不同时间点，对于任意0≤a

P*（b）-  P*（a）=（b2-a2）-20×（b-a）=（b-a）（b+a-20）≤（b-a）（2b-20）

由不等式可知，当b≤10时，有P*（b）≤  P*（a） ，若预计送达的时间是在早上10点之前，则越晚派送，收费越低。

类似地还有

P*（b）-  P*（a）=（b2-a2）- 20×（b-a）=（b-a）（b+a-20）≥（b-a）（2a-20）

当 a≥10时，有P*（b）≥  P*（a）  ，这意味着若预计送达的时间在早上10点以后，则越早派送，收费越低。

“如果我们选择让店家在早上10点，将蛋糕送达到咱们家的话，就能够让派送费最少了！”洛洛兴奋地向爸爸说出自己的结论。

爸爸欣慰地点点头，看来今年的生日对于洛洛而言，获得的不仅仅是年龄上的成长呢！