单模光纤章动跟踪耦合系统设计

吴天琦， 王睿扬， 王 超， 于笑楠， 佟首峰*

(1.长春理工大学 光电工程学院，吉林 长春 130022；2.长春理工大学 空间光电技术国家地方联合研究中心，吉林 长春 130022)

1 引 言

空间激光通信也称为无线光通信，是指利用激光束作为载波在空间直接进行语音、数据、图像等信息传输的一种技术，具有体积小、功耗低、机密性高、安全性高、数据速率高等优势[1-5]。单模光纤(Single Mode Fiber，SMF)耦合技术是光纤激光通信系统的关键技术，由于光纤静态角偏差、随机角抖动误差、大气湍流像差等因素的影响，SMF耦合损耗的光功率较大，因此提高SMF的耦合效率成为多年来国内外的研究热点[6-8]。

1990年，美国麻省理工学院提出了一种光纤章动的有源耦合方案，该方案结构简单，其实验系统中跟踪带宽约为1 kHz，耦合效率为63%[9]。2002年，美国的Weyrauch采用了盲优化的自适应光纤耦合系统来校正大气湍流引起的波前畸变，实验测得该系统单模光纤耦合效率约为60%[10]。2007年，电子科技大学提出优化耦合透镜的直径与焦距的比值的方法，耦合效率为61%[11]。2012年，日本Takenaka等制造了一种可在大气湍流下以高频率工作的快速转向镜，以提高光纤耦合效率，但这两个子光路结构复杂且容易引入人为误差[12]。2016年，上海光机所提出了基于激光章动的自动耦合方案，该方案中将耦合效率为73.5%，提高了6.5%[13]。2017年，成都光电所黄冠等提出基于FPGA平台的光纤耦合方案，应用SPGD算法实现了150 Hz的校正带宽[14]。2019年，长春光机所研究了能量反馈的单模光纤章动耦合算法并进行实验，实验结果表明在一定范围内该算法对动态扰动有明显抑制作用[15-16]。

在实际应用中，受大气湍流、机械平台振动、人为装调误差等因素的影响，空间光到单模光纤的耦合难度极高，严重制约空间激光通信系统的工作效果，故需要采用高效光纤耦合技术。本文基于空间光到单模光纤耦合理论，提出基于激光章动的高效耦合方法，通过单个光电探测器对耦合进单模光纤的能量进行检测，即可计算出光斑与光纤间的径向偏差，然后通过执行器实时补偿此偏差，实现耦合效率的提高。本文首次对激光通信载荷的平台振动对少模光纤耦合效率的影响进行了理论研究；基于激光章动方法，在光斑与光纤径向偏差很大时(光斑与光纤在初始未重合)，实现光斑对光纤的快速扫描、捕获、跟踪，完成空间光到单模光纤的高效耦合。而且本文实验中所用的振镜较其他实验中的波前传感器具有光路简单、成本低等优势。

2 单模光纤模场匹配原理

本文研究采用基于单模光纤的激光章动跟踪技术提升空间光到单模光纤的耦合效率，在讨论激光章动跟踪技术前，首先介绍单模光纤的模场匹配原理，并分析了基于单模光纤的激光章动跟踪技术可实现的最高耦合效率。

图1 单模光纤模场简化模型Fig.1 Simplified model of single mode fiber mode field

在大气中传输的激光信号经过口径为D、焦距为f的透镜汇聚后，在焦平面形成一个艾里斑，如图1所示。图1中ω1为艾里斑半径(ω1=1.22λf/D)，半径ω0为单模光纤模场半径。则空间光到单模光纤的耦合效率可以表示为[17]：

(1)

式中；A(r)为艾里斑模场分布，M(r)为近似高斯分布的单模光纤基模模场。A(r)与M(r)的表达式分别为：

(2)

(3)

式(2)中:r为光斑任意位置到光斑中心的径向距离，λ为信号光的波长，J1为一类零阶贝塞尔函数。当艾里斑与光纤间存在径向偏差ρ时，M(r)可表示为[14]：

(4)

式中:I0为零阶修正贝塞尔函数。将式(4)代入式(1)，可推导出与径向偏差有关的耦合效率表达式为：

(5)

根据公式(5)可计算出，当光斑半径与光纤模场半径满足ω1/ω0=1.711且两者中心完全重合时，耦合效率可以达到的最大值η=81.45%。由以上公式中的变量间的关系得到图2中耦合效率与光斑大小、径向偏移之间的关系。图2中纵坐标为耦合效率，横坐标为光斑半径与光纤模场半径的比值，不同颜色曲线表示不同径向偏移时的耦合效率。从图中可以看出，随着径向偏差的增大，耦合效率急剧下降，因此要对径向偏差进行补偿。

图2 耦合效率与光斑大小和径向偏移的关系仿真曲线Fig.2 Simulation curves of coupling efficiency versus spot size and radial offset

3 系统组成及算法设计

3.1 章动跟踪系统组成

激光章动系统组成如图3所示，包括激光器、准直镜、快速反射镜(Fast Steering Mirror，FSM)、耦合透镜、雪崩光电二极管(Avalanche Photo Diode，APD)及控制系统。激光器发射的光束首先经过准直镜进行扩束，然后入射快速反射镜进行径向偏差补偿与激光章动，接着通过耦合透镜聚焦并耦合到单模光纤内，再由APD检测光功率，最后将APD输出的信号传输至控制系统。控制系统对光纤位置进行计算，并将信号反馈到快速反射镜中，以实现径向偏差补偿和章动幅度的优化。

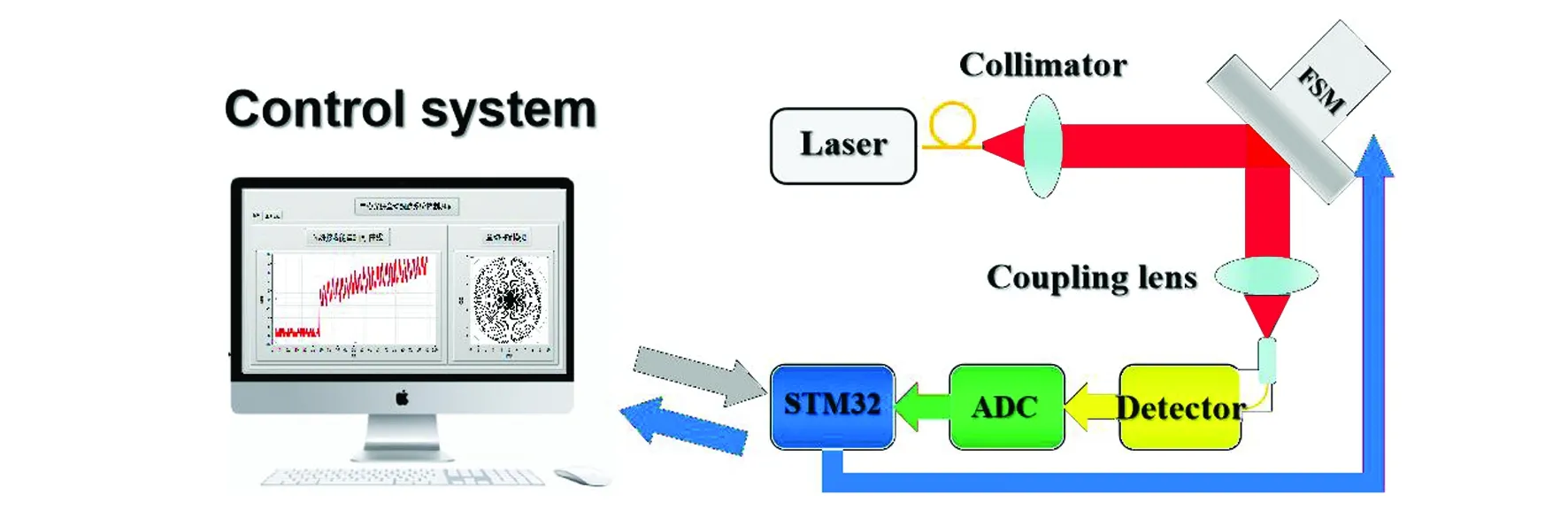
图3 激光章动系统Fig.3 Laser nutation system

3.2 章动跟踪系统算法设计

当光纤与光斑间存在径向偏差时，耦合效率的表达式为：

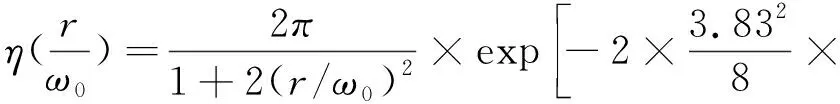
(6)

基于上式进行激光章动算法设计。在光束经过耦合透镜汇聚后，假设光斑能量Pin保持不变，设艾里斑尺寸为1.711ω0，章动扫描半径为ω0。首先，考虑初始状态下光斑与单模光纤未重合的情况。如图4(a)所示，初始时刻光斑中心On与光纤中心Of间距为βω0(β为一未知实数)，光斑以On为圆心做半径为ω0的圆形章动扫描，其扫描轨迹为图中蓝色虚线。显然，此过程中光斑与光纤(黄色圆形)不会发生重叠。改变章动扫描半径为2ω0，光斑扫描轨迹为图中绿色虚线，此时光斑与光纤仍未发生重叠。接下来，进一步增大扫描半径，直到扫描半径大于黑色虚线轨迹半径，光斑与光纤发生面积重叠，探测器检测到能量。当探测器开始有信号输出时，系统开始改变扫描策略，以某一小幅度Δrc-n增大光斑章动扫描半径，如图4(b)所示。设章动扫描中心为坐标原点，rc-n1为光斑(圆形红色实线)与光纤首次重叠时的扫描半径，当光斑与光纤重叠面积最大时，光斑与光纤间距为rc-1，光斑在整个扫描周期内仅会出现一次与光纤面积重叠最大的情况，相应地，探测器仅在一个时刻内输出最大值Pc-max1。改变章动扫描半径为rc-n2，当光斑位于红色虚线圆圈位置时，与光纤重叠面积最大，此时两者间距为rc-2，探测器输出最大值为Pc-max2。上述过程为激光章动粗扫描阶段，满足如下数学关系[18]：

(7)

(8)

rc-2-rc-1=rc-n2-rc-n1=Δrc-n，

(9)

(a)光斑与光纤无重合(a)Spot without coincideence with fiber

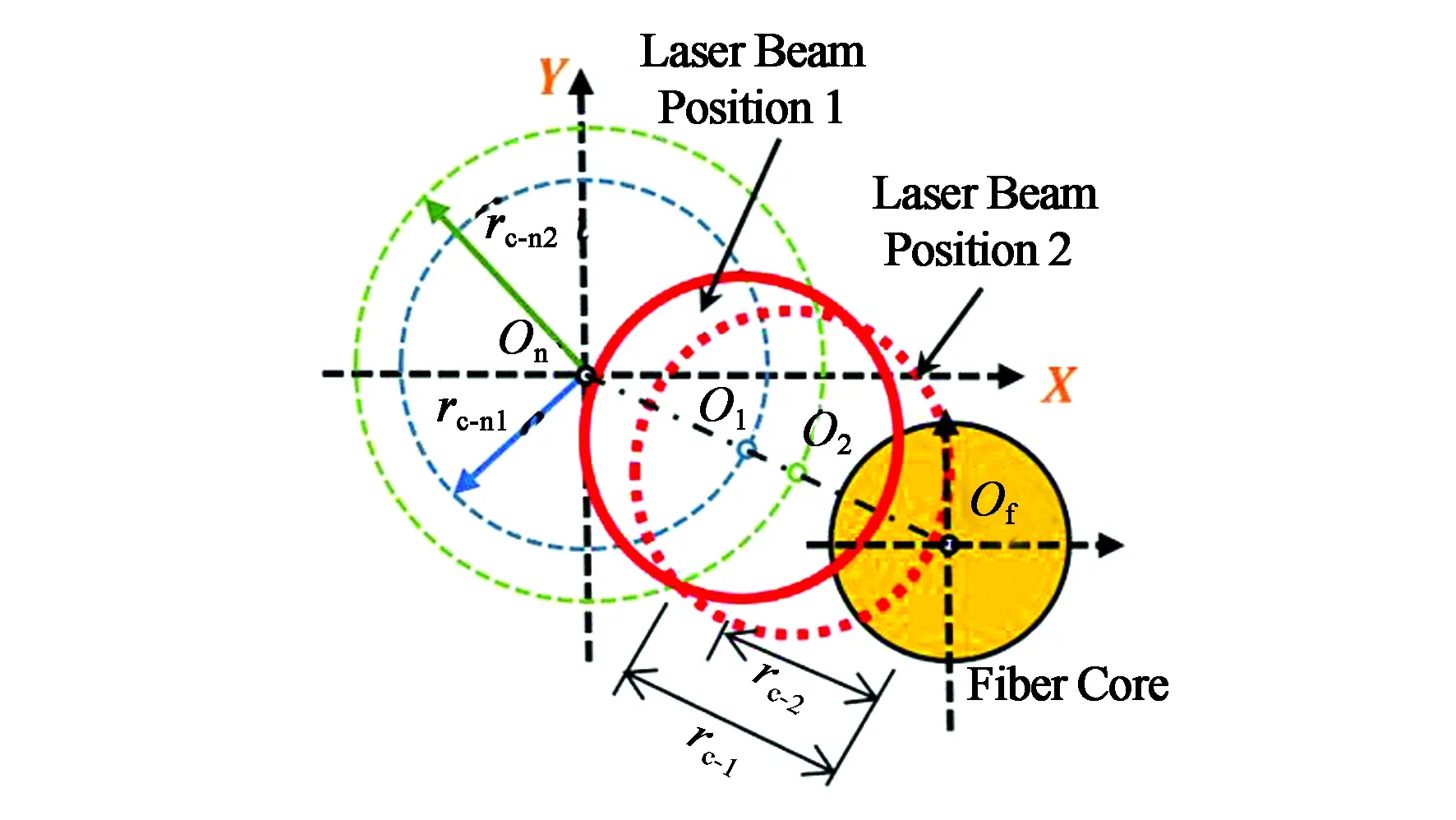
(b)光斑与光纤有重合(b)Spot overlap with the fiber图4 激光章动粗扫描阶段原理Fig.4 Principle of laser nutation coarse scanning stage

光纤中心到光斑中心的横向偏移量xfiber与纵向偏移量yfiber的表达式分别为：

(10)

式中:ω为章动扫描角速度，t为时间。通过上式可计算出光纤中心的相对位置坐标(xfiber,yfiber)。得出光纤位置坐标后，通过快速反射镜进行径向偏差补偿。因采样点数量有限，故通过计算得到的光纤坐标并不精准，为了加快粗扫描阶段的捕获过程，实现光斑与光纤大部分重叠即可。为了获得精确的坐标，需要进一步的精扫描。

经粗扫描与补偿后，光斑中心与单模光纤中心已经比较接近，但影响耦合效率的径向偏差仍然存在。图5为激光章动精扫描阶段示意图。图中蓝色虚线为精扫描阶段的章动轨迹，由于径向偏差的存在，圆形扫描轨迹rc-n与光纤并不同心。可见，扫描过程中光斑与光纤始终有重叠部分，探测器有持续输出，且在每个扫描周期内均有最大与最小值出现。探测器输出最小值Pf-min时，光斑与光纤径向偏差为rf-max；探测器输出最大值Pf-max时，光斑与光纤径向偏差为rf-min，则有如下关系：

(11)

(12)

rf-max+rf-min=2rf-n.

(13)

光纤的中心位置坐标的表达式为[16]：

(14)

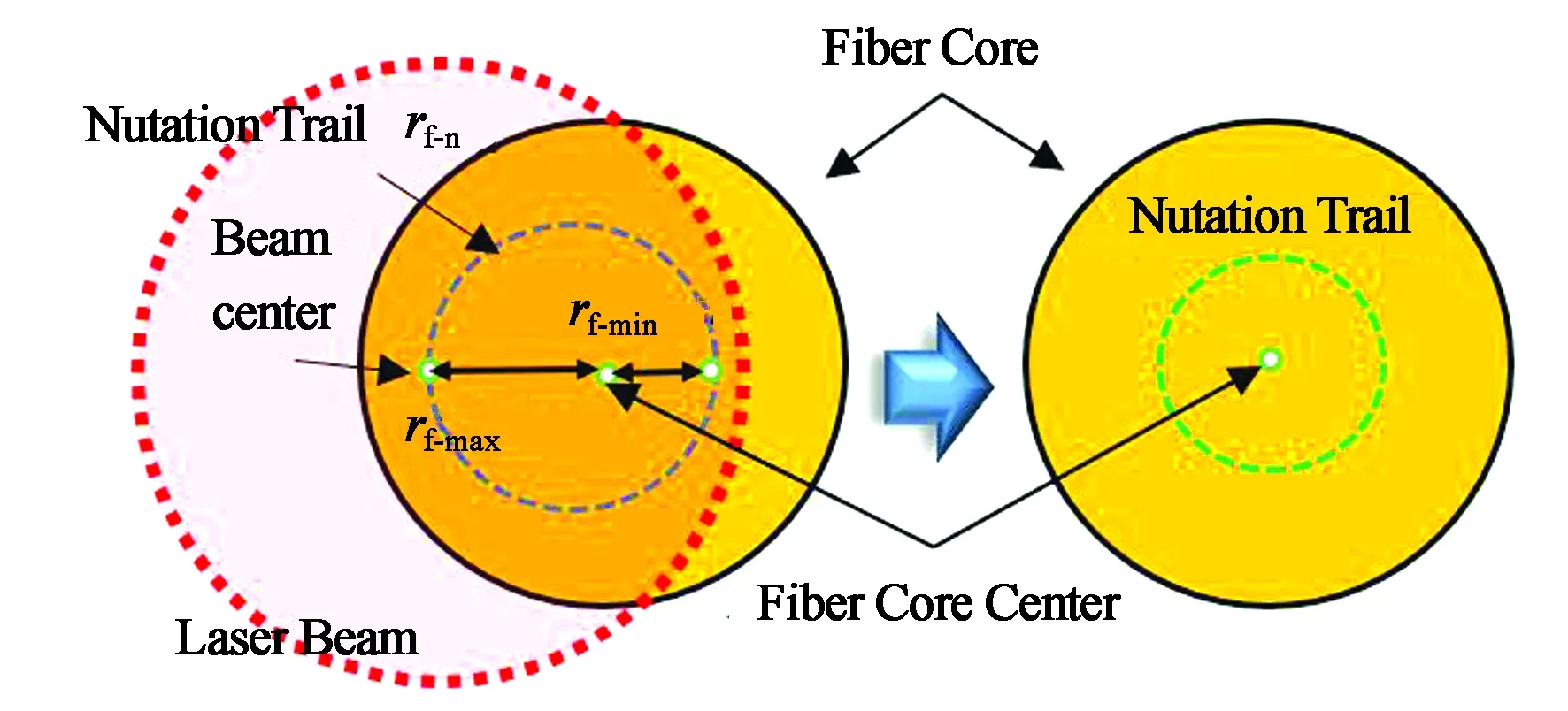
图5 激光章动精扫描阶段原理Fig.5 Principle of laser nutretization scanning phase

根据计算结果，通过快速反射镜进行径向偏差补偿，使光斑中心与光纤中心完全重合。接着，使光斑以某一幅度绕光纤中心进行章动扫描，如图5中绿色虚线所示。根据圆的对称性，在此扫描周期内，光斑与光纤间存在一固定径向偏差，两者重叠面积不变，探测器输出信号的平均功率不变。此固定径向偏差的存在目的是抵消随即抖动引入的偏差。整套系统算法流程如图6所示。

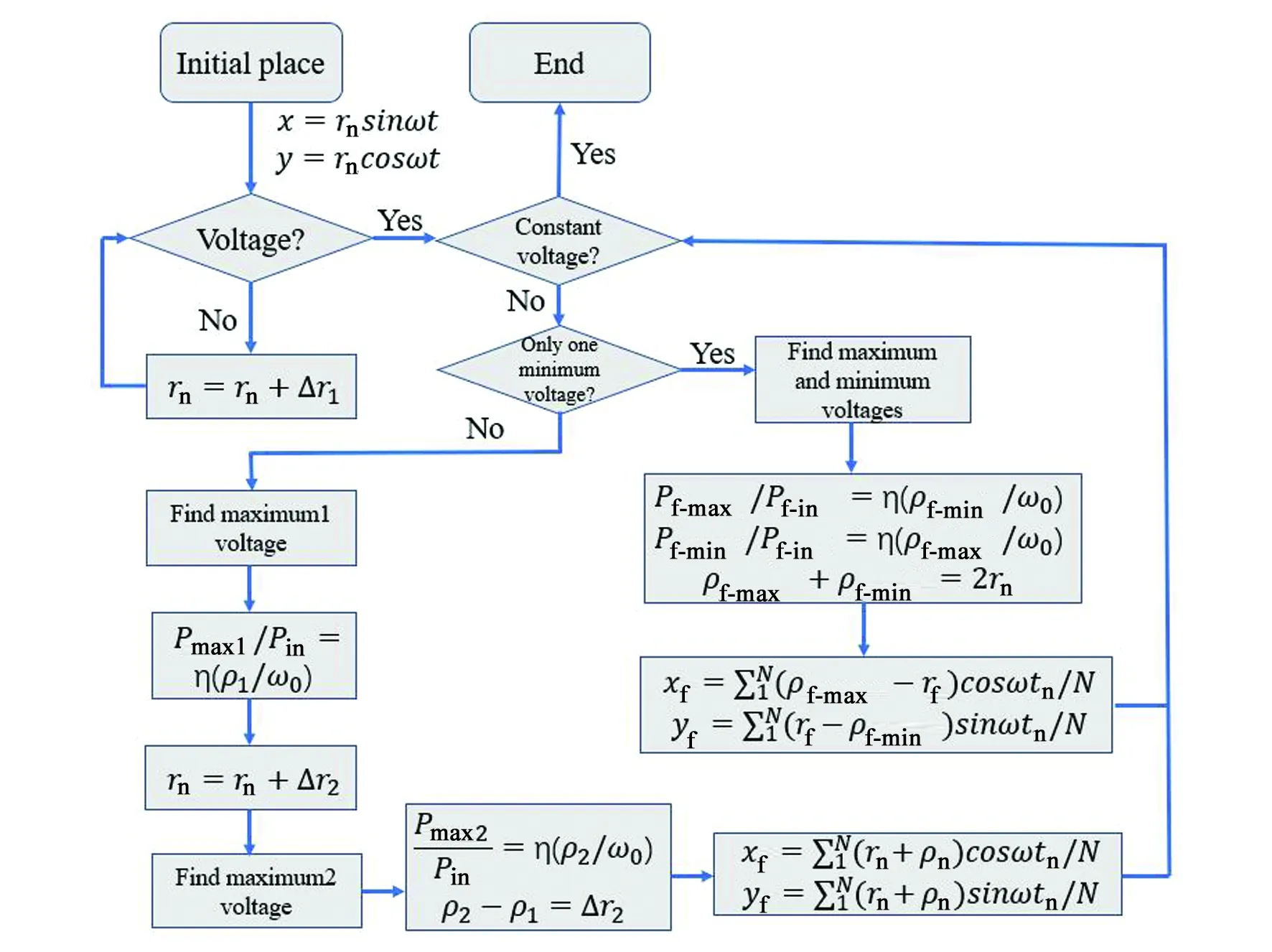
图6 章动算法流程Fig.6 Nutation algorithm flow

4 实验测试及结果分析

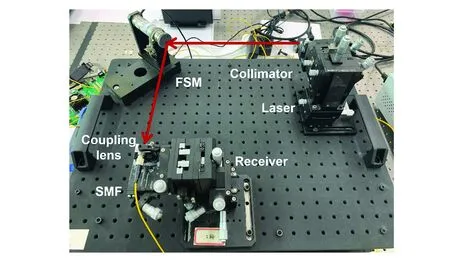
图7 章动系统实验平台Fig.7 Nutation system experiment platform

根据上文的章动原理、系统组成以及算法设计，本章针对激光章动跟踪系统的性能进行实验测试。实验平台的搭建如图7所示，激光束从光纤出射后，首先经过准直镜，然后通过快速反射镜进行偏转，再经过准直镜后进入光纤，从而进入APD。同时，采用光功率计监测激光器的发射功率与通过耦合进入光纤的光功率。实验器件选型如表1所示。

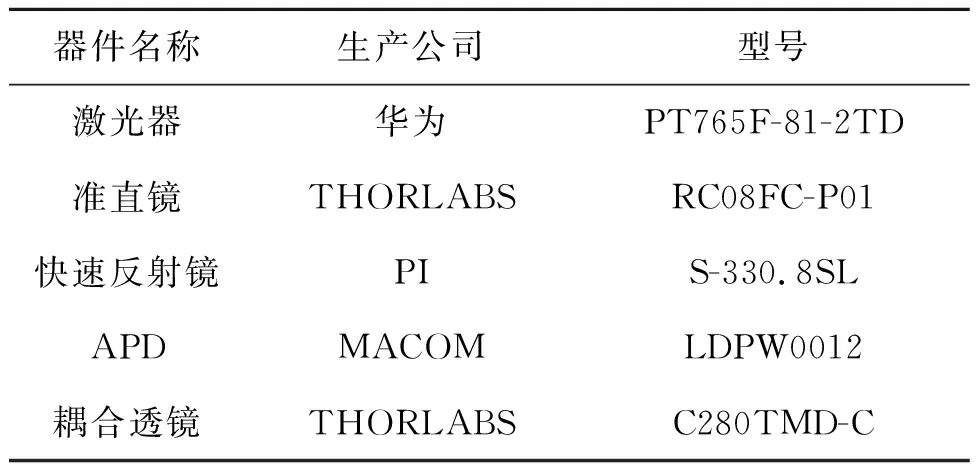
表1 实验器件选型Tab.1 Experimental device selection

4.1 耦合效率测试

耦合效率是章动跟踪系统最重要的性能参数，直接决定了空间光耦合到光纤中的光功率。在实验中，采用波长为1 550 nm的激光器作为光源，如图8所示，其发射光功率为-6.98 dBm。

图8 激光器发射光功率Fig.8 Laser emitting optical power

图9 章动中心逐渐向光纤中心收敛时APD输出的电压Fig.9 Voltage of the APD output when the nutation center gradually converges toward the center of the fiber

首先进入章动粗扫描阶段，此时章动半径逐渐扩大，直到APD检测到信号光，产生电信号后，开始进行章动精扫描。根据APD输出信号的强度变化，章动中心逐渐向光纤中心收敛，章动半径逐渐减小，章动扫描阶段APD输出电压如图9所示。从图中可以看出在粗扫描阶段完成对信号光的捕获后，随着章动中心逐渐向光纤中心收敛以及章动半径逐渐减小，APD输出信号逐步提升。

直至APD输出信号的平均值保持恒定，实现章动中心与光纤中心重合，此时APD输出信号的曲线如图10所示。从图中可以看出APD输出信号的强度仍有抖动，但抖动范围保持不变，以此判定系统实现了章动跟踪。实现章动跟踪后，耦合进入单模光纤的光功率为-9.70 dBm，如图11所示。通过计算得到系统的耦合效率为53.5%。

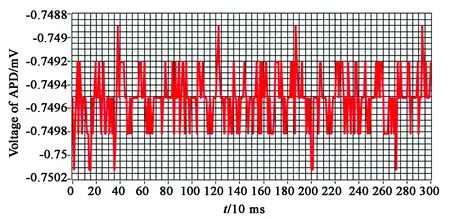
图10 章动中心与光纤中心重合时APD输出的电压Fig.10 Voltage of the APD output when the nutation center coincides with the fiber center

图11 章动跟踪时耦合进入光纤的光功率Fig.11 Optical power coupled into the fiber during nutation tracking

4.2 径向偏移对耦合效率的影响

本文第二章根据理论分析了径向偏移和光斑半径对耦合效率的影响，本节将针对径向偏移的影响对系统进行测试。测试中，以光纤中心为原点建立坐标系，保持光斑面积不变，分别测量不同章动中心至光纤模场中心距离时的耦合效率。实验数据如图12所示，从图12中可以看出随着径向偏移增大，耦合效率降低，其变化趋势与理论分析的一致。

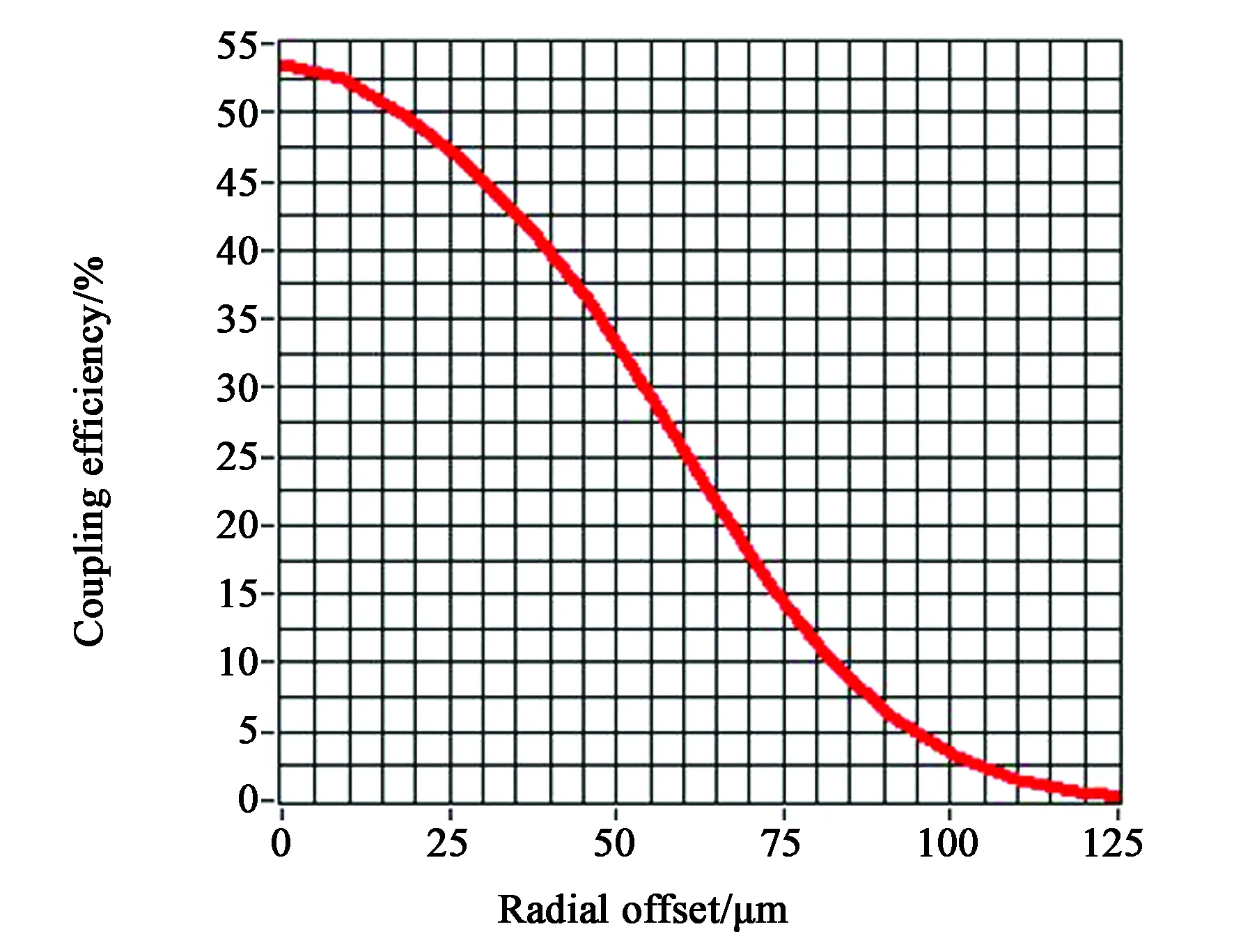
图12 径向偏移与耦合效率的关系曲线Fig.12 Radial offset and coupling efficiency

4.3 光斑半径对耦合效率的影响

本节针对光斑大小对耦合效率的影响对系统进行测试。测试中，保持径向偏移不变且为最小值，通过改变耦合透镜的工作距离以实现不同光斑半径时的耦合效率的测量。实验结果如图13所示，从图13中可以看出当光斑半径与单模光纤模场半径的比值为1.711倍时，耦合效率最大，当光斑半径发生变化时，耦合效率的变化趋势与理论分析的一致。

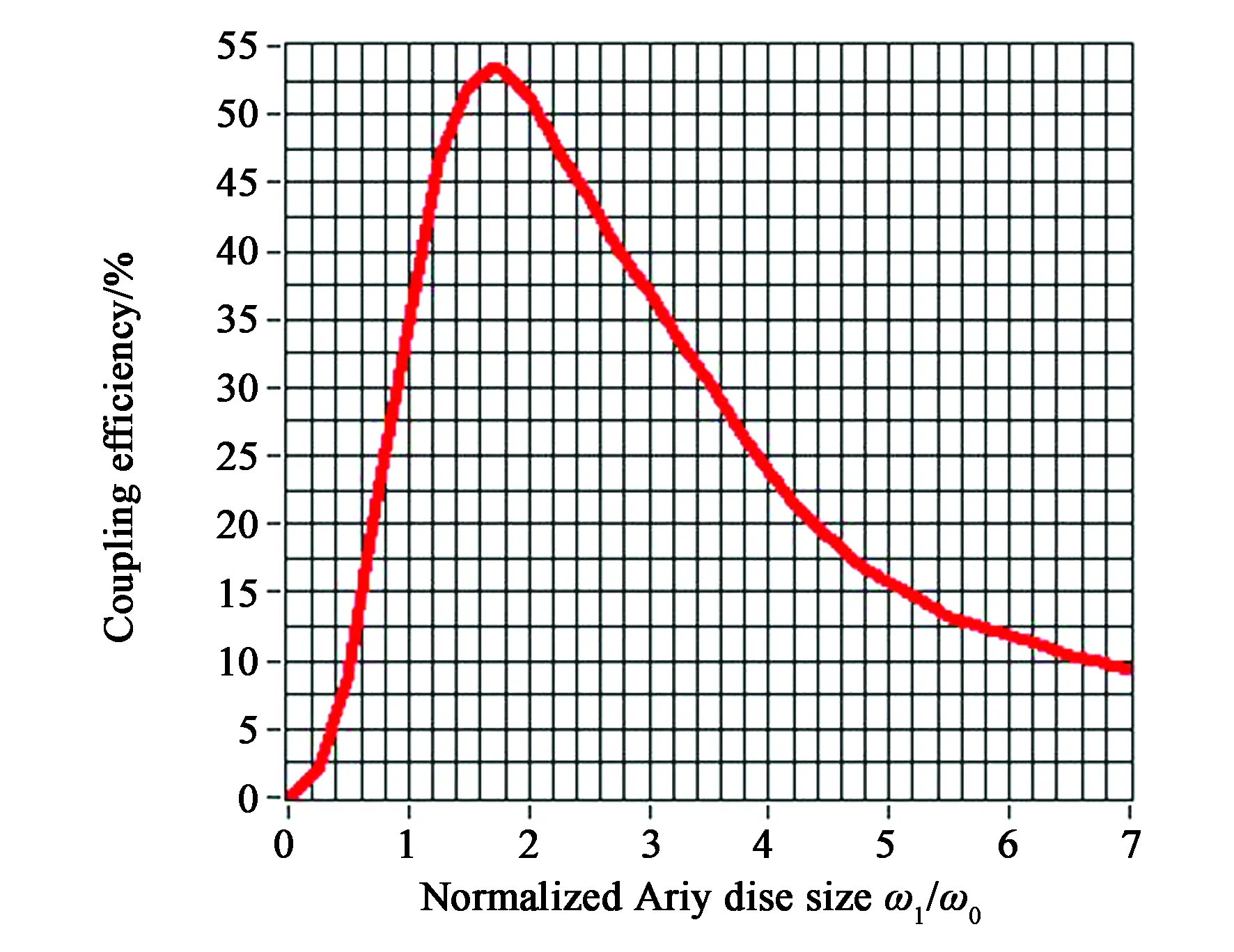
图13 光斑半径和单模光纤模场半径的比值与耦合效率的关系曲线Fig.13 Relationship between the ratio of the spot radius and the mode field radius of a single-mode fiber to the coupling efficiency

5 结 论

本文根据单模光纤的模场匹配原理进行了激光章动跟踪系统以及算法设计，通过实验测得在激光章动跟踪时单模光纤的耦合效率最高为53.5%。并对径向偏差以及光斑大小对耦合效率的影响进行了测试，得到了径向偏移与耦合效率的关系曲线以及光斑半径和单模光纤模场半径的比值与耦合效率的关系曲线。通过与理论分析的仿真曲线进行对比，其变化趋势一致。根据理论分析，径向偏差对耦合效率的影响最大。实验结果与理论分析仍具有一定差距，本文设计的章动算法及采用的硬件对实验结果均存在影响。硬件方面的影响主要包括APD及放大电路的噪声、A/D及D/A的精度、振镜的精度以及光路误差；软件方面主要有章动半径、收敛步长及采样点个数对耦合性能的影响。这些因素都导致实际耦合效率降低。在下一步的研究中将针对以上因素对系统进行完善，从而获得更高的耦合效率。