高速铁路桥梁挡风屏遮蔽效应分析

霍 卿, 许建林, 梅元贵,*

(1. 唐山学院 交通与车辆工程系, 河北 唐山 063000;2. 兰州交通大学 甘肃省轨道交通力学应用工程实验室, 甘肃 兰州 730070)

0 引 言

百里风区是指兰新铁路红旗坎站至了墩站全长123 km的区间，区间内多含桥梁[1]，该区间全年有320天刮8级以上大风，12级以上的强风经常出现，且盛行风向主要集中在东北东(NNE)至北西北(NNW)，是我国乃至世界上铁路风灾最严重的地区之一[2-4]。

在大风作用下,列车空气动力性能恶化,强风不仅影响列车的横向稳定性,还会导致列车空气阻力迅速增加或聚降[5]；大风中运行产生的振动可能导致供电出现异常；气动噪声给司乘人员带来的影响也非常明显。这些都严重影响了行车的安全性和乘坐的舒适性[6-8]。据不完全统计，自1960年至今，新疆铁路运输因风沙造成的行车安全事故总计38起。因大风造成的列车停轮次数更是数不胜数，严重影响了铁路运输的经济效益[9]。

为减缓风害，提高列车安全运行和旅客的乘车舒适性，在大风区线路建设工程中一般加装挡风设施。常见的挡风设施主要有不透风的挡风墙和可透风的挡风屏。路堑和路堤上多采用挡风墙， 桥梁上多采用挡风屏，以减小结构风载荷[10]。由于挡风屏的多孔结构，流体通过后与挡风墙结构相比流动变得复杂。因此，正确评价挡风屏的遮蔽效应更为重要，也是保证列车安全运行的重要前提和挡风屏抗风补强设计的重要依据。

目前，国内外针对挡风屏的遮蔽效果开展了较多的研究。国内方面：项超群采用真实模拟列车运动的动网格算法，计算不同挡风屏高度下桥上列车的气动力系数，研究列车周围流场静压分布和速度分布，并与传统静网格计算结果进行对比分析[11]。张田[12]、向活跃[13]、梅群峰[14]等应用数值模拟方法，在模型的特定断面上取测点，通过对压力、速度等参数的比较，在横风条件下对不同类型挡风屏的高度、开孔率、布置形式等参数进行了研究。邹云锋、何旭辉基于同步测压方法，以京沪高速铁路典型高架桥和CRH2列车为背景，研究了多种挡风屏参数对典型车桥组合状态下车辆气动力和风压分布的影响，分析挡风屏的气动影响机理[15-16]。何玮、郭向荣通过风洞试验得出在桥梁上设置不同透风率挡风屏情况下桥梁和桥上不同位置处列车的三分力系数，并研究挡风屏透风率对侧风下大跨度斜拉桥车桥系统耦合振动的影响[17-18]。以上研究主要针对挡风屏前期合理设计形式和主要参数的合理取值。另外，如郭微微[3]和唐煜[19]等通过数值模拟的方法，对横风条件下考虑车、桥、屏三者耦合系统下的车辆行车安全性进行了评价，但模型中未涉及风向、风速、毗邻结构等因素的影响。

国外方面： Fujii等[20]、Baker 等[21]阐述了日本和欧洲的挡风屏措施。Shunji Takahashi等[22]在横风下考虑结构与地形地貌的相互作用，取典型断面对不同开孔率挡风屏的遮蔽效果进行了数值模拟研究。Crosby等[23]在横风条件下，考虑挡风屏和房屋的简单模型的相互作用，对渗透式挡风屏对房屋结构的风场遮蔽效果特性进行了研究，但以上作者在模型中均未考虑桥梁的影响。

文献[24]表明风对于结构的影响与风向有关。横风条件下建筑结构风载气动特性不具有典型性[25]。另外，当建筑群结构相互间距较近时，由于旋涡的相互干扰，建筑结构某些部位的局部风压会显著增大[26]。可见，当对挡风屏结构进行遮蔽效应评价时，仅考虑横风工况，而不考虑桥梁以及毗邻建筑、风速风向、地形地貌等因素影响下的气动特性是远远不够的，还需要对挡风屏实地的遮蔽效应进行研究。

综上所述，基于目前国内外学者对于挡风屏的研究主要集中前期结构合理设计、以及在横风工况下仅以挡风屏本身作为研究对象较少结合实地工况对挡风屏的特性进行研究的条件下，本文通过三维数值模拟方法，以百里风区吾普尔大桥上透风式挡风屏为研究对象，模型尽量还原真实的现场环境，考虑挡风屏本体及周边地形地貌(坡度约3.1%)及相邻挡风设施，如：防风明洞、挡风墙、吾普尔大桥等，并结合不同断面位置、风向角、风速、线路布局等影响因素对挡风屏遮蔽效应进行研究，为挡风屏的抗风补强设计及列车安全运行提供合理的参考依据。

1 挡风屏结构介绍及模型展示

1.1 挡风屏结构介绍

挡风屏位于百里风区的核心地带的吾普尔大桥上，为双侧设置、与桥梁本体连接的板式挡风屏结构。全长241m，高4m，屏体上部和下部分别由开孔率为10%和20%的长圆形开孔波纹板组成，是一种新的结构，其西侧与防风明洞入口相连，东侧一端直接与挡风墙相连。图1和图2分别给出了挡风屏的结构示意图和实景图。

图1 挡风屏结构Fig.1 Windshield structure

1.2 挡风屏模型展示

本文采用1∶10计算模型，挡风屏全长24.1 m，高0.4 m(以挡风屏高度为特征尺度H)，整个计算域为290H(长)×100H(宽)×100H(高)。静态网格绕流计算模型如图3所示，并尽可能保持挡风屏毗邻结构如：防风明洞、挡风墙、桥梁(吾普尔大桥)、路基、涵洞、地形地貌(其中挡风屏防风明洞端地貌形成了明显的路堑结构)等环境特征，几何结构真实、复杂，如图4、图5所示。

(a) 挡风屏防风明洞端(西侧)

(b) 挡风屏挡风墙端(东侧)

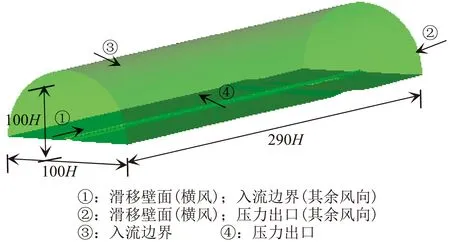
图3 模型计算域及边界条件Fig.3 Model computation domainand boundary condition

图4 模型端口细节Fig.4 Model port detail

(a) 桥梁及挡风屏细节

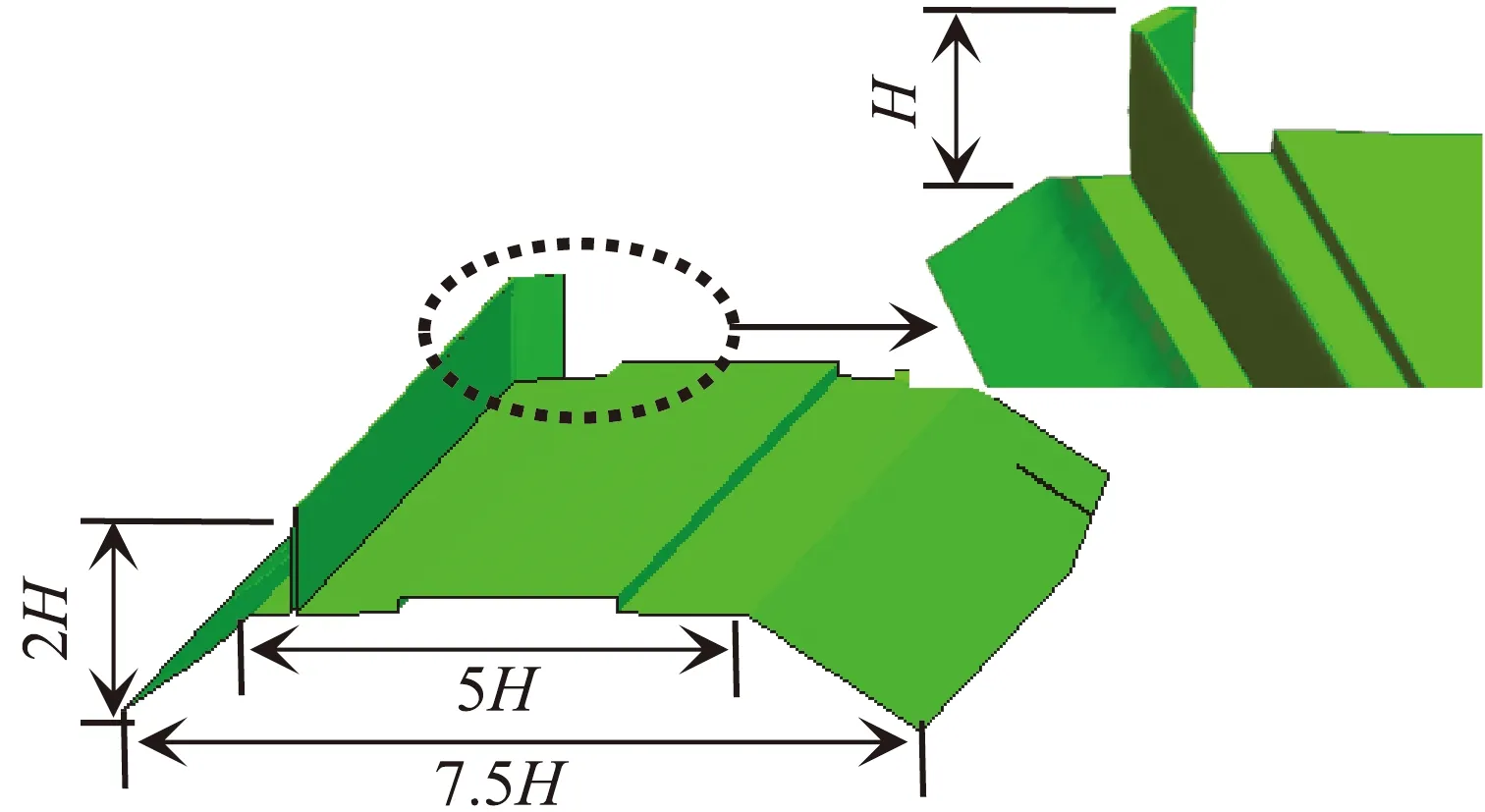
(b) 路基及挡风墙细节

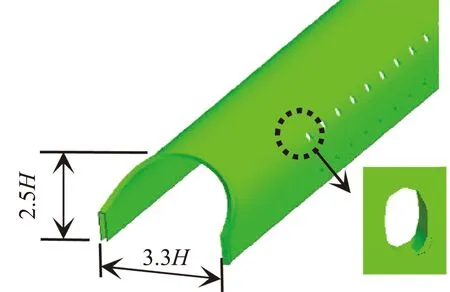
(c) 明洞端口及通风孔细节

2 数值计算方法及定解条件

2.1 数学模型及控制方程

本文采用STAR-CCM+ 11.02进行空气动力学分析，防风明洞外部的空气按有黏性体处理，采用SSTk-ω高雷诺数湍流模型数值求解防风明洞外部的三维定常不可压缩湍流流动，即求解连续性方程、动量方程和SSTk-ω湍流模型方程。

连续性方程

(1)

动量方程

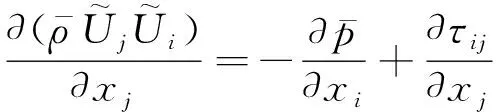
(2)

式中：上标“—、～”分别表示物理量的时均、质量加权平均和脉动量，ρ、p、Ui分别为空气的密度、压力(表压)、速度，τij为平均运动的应力张量。

湍流的模拟采用SSTk-ω模型，其控制方程为：

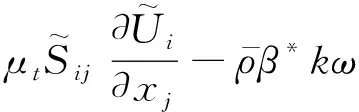
(3)

(4)

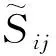
2.2 边界条件

向活跃[13]采用风洞模型试验和数值模拟方法，评估了不同开孔率的圆形孔挡风屏防风效果，并指出数值研究中采用挡风屏的多孔介质模型对结果影响不大，且能有效减少网格数，降低计算规模。因此本文模拟的各种风向角、风速等大风绕流挡风屏的工况，挡风屏按照多孔介质处理，防风明洞、挡风墙、桥梁、路基和地面等为无滑移静止壁面。洞外开阔空间在横风条件下设置滑移静置壁面、速度入口和压力出口，其余风向角工况为速度入口和压力出口，如图3所示。图6表示了风速、风向与桥梁挡风屏关系的俯视图，其中β为风向角，Uw为风速。

图6 风向角示意图Fig.6 Schematic diagram of wind direction angle

本文缩比模型的计算网格采用非结构混合网格，其中外流场主要采用六面体核心网格(Trim 网格)，在桥梁、挡风屏、防风明洞、挡风墙等部件均采用棱柱网格 (Prism 网格)，这样可以更好地模拟粘性占主导区域的流动[27]。为了保证棱柱网格和六面体核心网格间的良好过渡，在明洞模型表面的棱柱网格设置为6层，网格增长比为1.2，图7表示了桥梁、挡风屏计算网格分布情况。在缩比模型周围，尤其是缩比模型尾流区域设置了网格加密区，总体计算网格量达到5200万左右。

本文采用多孔介质方法对挡风屏进行处理，计算过程中认为防风屏为无厚度含开孔的挡板结构，图5(a)。遵从达西准则，流体的流速与流体的压力降建立控制方程：

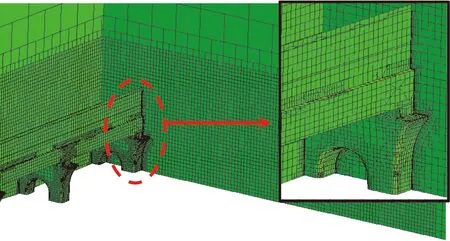
图7 梁挡风屏局部网格展示Fig.7 Local mesh display

Δp=-ρ(α|vn|+β)vn

(5)

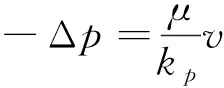
(6)

式中：Δp为流体流经多孔介质的压力降；ρ为流体密度；vn为入流多孔介质的表面流速；α、β为与开孔率相关的系数；kp为渗透率；v为流体流经多孔介质后的流速。

本文中α、β的取值按文献[3]对兰新线挡风屏进行数值模拟的结论并进行了算法有效性验证。

3 挡风屏遮蔽效应分析

3.1 评价准则与测点布置

速度是挡风屏防风效果重要的评价准则之一。由于挡风屏对来流的影响，侧向风在流经桥面时会形成分布不均匀的涡旋结构，导致同一位置距离桥面不同高度处的风速是不同的。为了衡量挡风屏的防风效果，可以根据一定高度内侧向气动力等效的原则来定义桥面等效风速，即[28]：

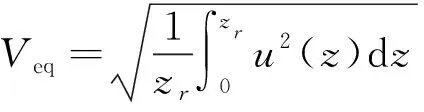
(7)

式中zr为等效高度范围，本文取值为路基板面到挡风屏顶部高度0.45 m。

挡风屏的防风效果可以用桥面等效风速与来流风速的比值，即局部风速折减系数λ表示：

λ=Veq/V

(8)

式中V为桥面高度来流风速。

公式(8)是对结构整体的防风效果的评价，若仅对距离桥面某一高度处特征点的防护效果进行评价，可以用局部防护系数I来表示某特征点处的防护效果，定义为：

I=1-|u(x,z)|2/V2

(9)

式中u(x,z)为特征点处的局部风速。

计算出整个防护区域内所有特征点的局部防护系数，然后取平均值，用于评价整个区域的防风效果。

考虑到毗邻防风明洞和挡风墙对挡风屏流场的影响，本文在距离挡风屏西侧接近防风明洞1H的位置、东侧接近挡风墙1H的位置、屏体中段位置各取断面作为分析对象，同时在各断面上行线(接近挡风墙一侧)和下行线两条线路中线布置测点，如图8所示。图中第一个点位置约为0.0625H，即轨面距离路基的距离，各测点间距0.125H，最高测点与挡风屏顶端平齐。

3.2 典型断面遮蔽效果分析

图9给出横风条件下，风速40 m/s时，挡风屏防风明洞端、桥梁中段和挡风墙端三个断面上行线轨道中心线风速随挡风屏高度变化的曲线图和各断面的速度折减系数。由图9可以发现，挡风屏东西两端及其中段的遮蔽效应不同。从速度分布情况看，屏体中段风速集中在0～4 m，风速折减系数为0.08，遮蔽效果最佳。而对于挡风屏的挡风墙一端，风速集中在12～16 m。风速折减系数为0.33，遮蔽效果最差，防风明洞一端次之。

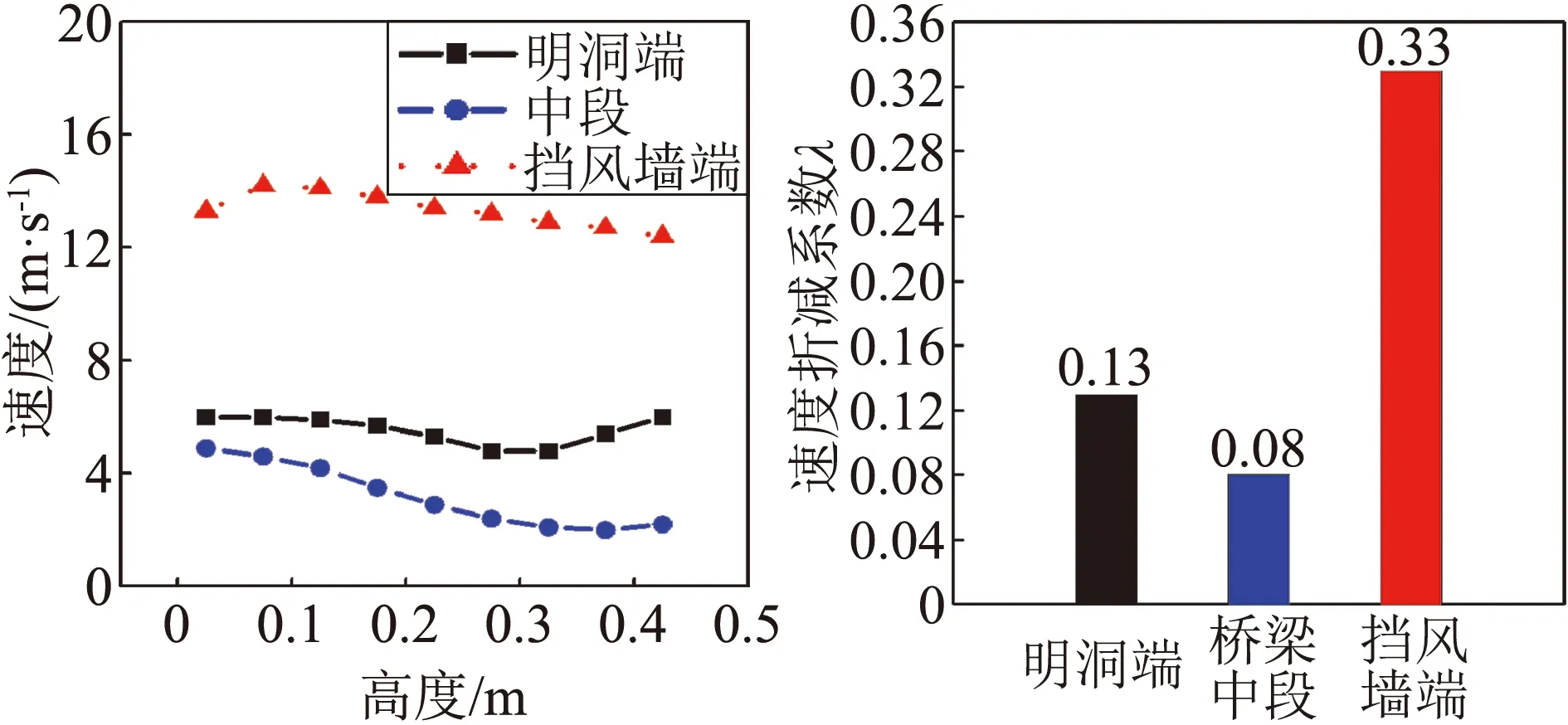
(a) 速度变化曲线 (b) 各断面速度折减系数

为了更好的展示建筑结构对挡风屏遮蔽效果的影响。分别在接近防风明洞、挡风墙与挡风屏衔接位置并靠近防风明洞和挡风墙一侧取断面。如图10表示了挡风屏西侧，防风明洞端口距离挡风屏0.1H位置断面和挡风屏东侧挡风墙距离挡风屏0.1H位置断面的速度矢量分布图。从图中可以看到，明洞端口和挡风墙一端的流体均是向挡风屏内流动，流进两个挡风屏之间的通道，增大了挡风屏西侧流体的能量，进而减弱了挡风屏东西两端的遮蔽效果。从速度幅值分布看，挡风墙一端的流体流动速度幅值相对较大，遮蔽效果较明洞侧要差。

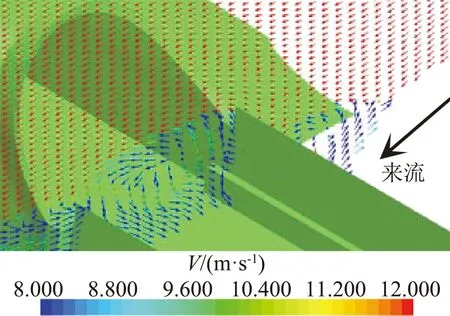
(a) 明洞断面

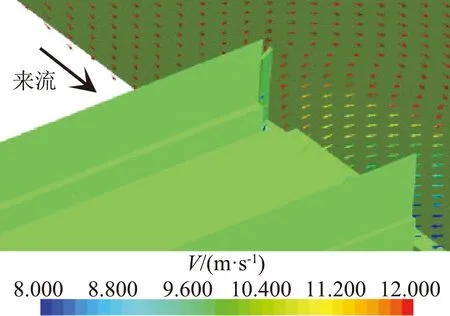
(b) 挡风墙断面

从图11三个断面的涡旋结构分布图可以看到，挡风屏防风明洞端由于两侧“路堑”式地貌结构，使得挡风屏两侧及流动通道内涡旋结构剧烈、明显，而桥梁中段和挡风墙端断面则无明显的涡旋结构。

通过上述分析可知，挡风墙及明洞端流体向挡风屏通道内流动是造成挡风屏两端和中段的遮蔽效果不同的主要原因。毗邻建筑结构会使挡风屏的遮蔽效果减弱。另外，地形、地貌使得挡风屏附近流场的涡旋结构增强。

3.3 不同线路遮蔽效果分析

线路不同，行驶列车受到的气动作用不同，鉴于兰新二线的双线路特点，本节讨论挡风屏对于不同线路的遮蔽效果分析。

图12表示了不同断面上行线和下行线速度曲线和速度折减系数柱状图。对于速度的比较，下行线速度均比上行线速度小，但防风明洞端挡风屏开孔率20%的部分呈相反特性。有速度折减系数比较可知，在防风明洞端和桥梁中段位置上行线与下行线的遮蔽效果相差不大，速度折减系数相差仅为0.01～0.02，但在挡风墙端挡风屏，下行线遮蔽效果明显优于上行线，速度折减系数相差为0.11，差值百分约27%。

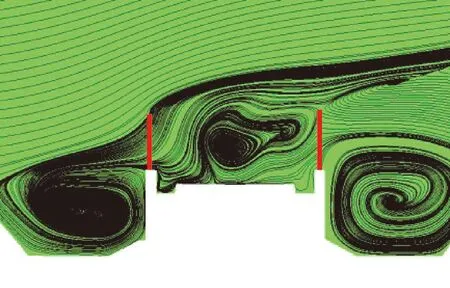
(a) 挡风屏防风明洞端断面

(b) 挡风屏桥梁中段断面

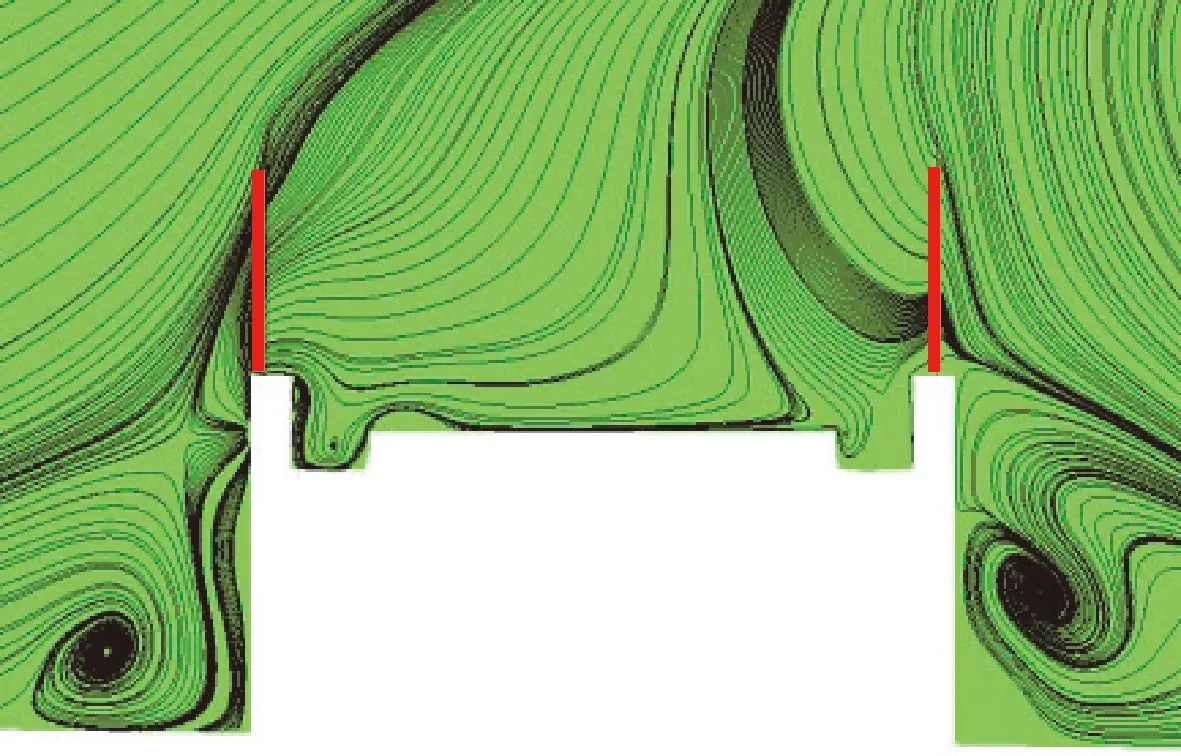
(c) 挡风屏挡风墙端断面

图11 各断面涡旋结构分布
Fig.11 Distribution of vortex structure of each section

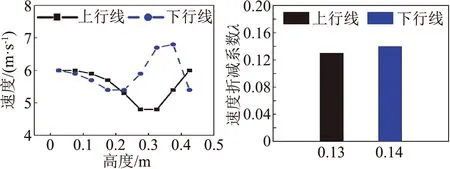
(a) 防风明洞端

(b) 桥梁中段

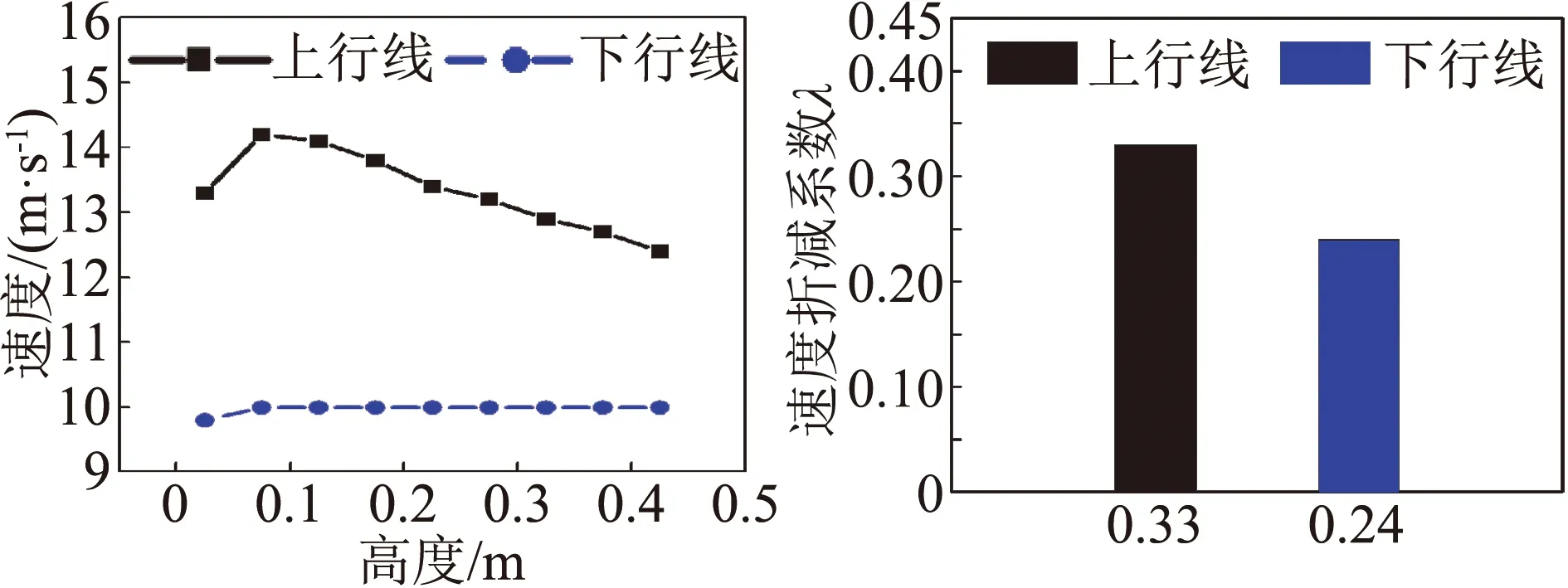
(c) 挡风墙端

图13表示了挡风屏东侧毗邻挡风墙距离挡风屏0.1H断面的涡旋结构分布。从图中可以看到，在挡风墙的背风侧产生了一个巨大的涡旋结构。结合图10(b)，不难发现涡旋结构的三维流动特性使得流体反流至两个挡风屏中间的通道内，且下行线流速明显低于上行线流速。使得下行线的遮蔽效果明显增强。

3.4 不同来流速度遮蔽效果分析

针对兰新二线风力强劲、多变的特点，本节讨论当来流风速变化时，对挡风屏遮蔽效果的影响。

图14给出了来流速度30 m/s、40 m/s、50 m/s下各断面上行线速度变化曲线。可见，随着来流速度的增大，各断面速度增大，且分布趋势相似。但是从图15不同来流风速下各断面各测点局部防护系数的平均值图可见，随着来流风速的变化，遮蔽效果变化不大，各断面平均防护系数幅值变化仅为0.001～0.002。

图13 东侧挡风墙断面涡旋结构分布Fig.13 Distribution of vortex structure of the east side windshield wall

(a) 防风明洞端 (b) 桥梁中段 (c) 挡风墙端

3.5 不同风向角下遮蔽效果分析

风向是影响结构气动载荷的主要因素之一。结合兰新二线多风向的特点，本节将讨论风向角对于挡风屏遮蔽效果的影响。

图16和图17分别给出了风向角15°～90°，不同断面上行线的速度曲线和各断面的平均防护系数。由图可见，风向角对速度的影响规律性较差。但整体趋势仍为小风向角时风速大于大风向角的风速。由图17可知，随着风向角的增大，各断面的平均防护系数基本成增大趋势，防护效果增强。这是由于当风向角增大时，流体垂直流过挡风屏的流体增多，相应的沿着挡风屏之间通道流入的流体减小。进而增大了挡风屏对流体的遮蔽效果。

(a) 防风明洞端 (b) 桥梁中段 (c) 挡风墙端

(a) 防风明洞端 (b) 桥梁中段 (c) 挡风墙端

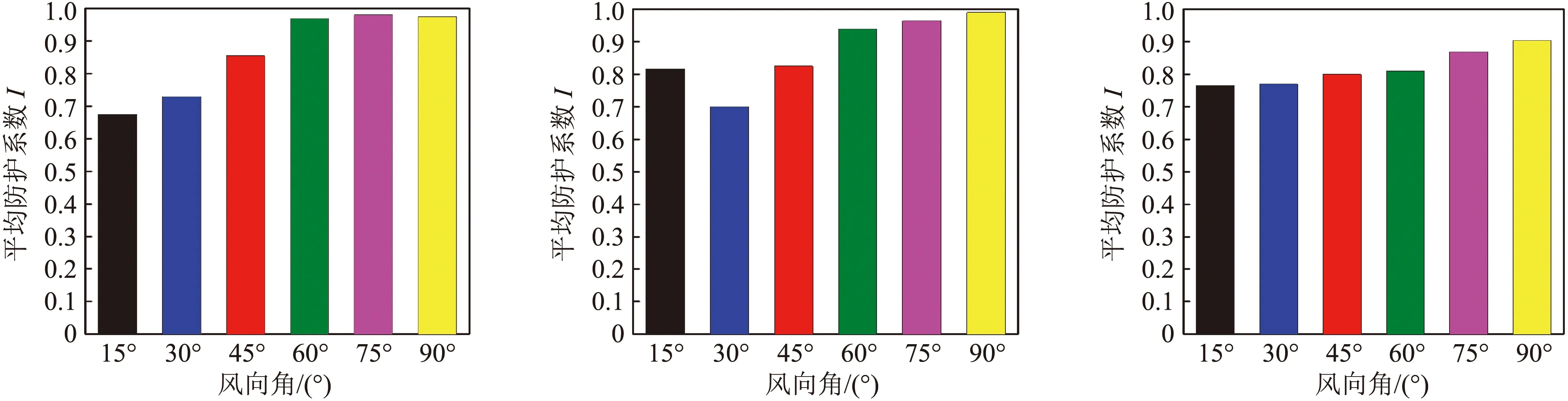
(a) 防风明洞端 (b) 桥梁中段 (c) 挡风墙端

4 结 论

通过数值模拟方法对兰新二线吾普尔大桥上挡风屏特性进行研究，模型尽量还原真实的现场环境，考虑了挡风屏本体及周边地形地貌及相邻挡风设施，得出：

1) 挡风屏两端和中段的遮蔽效果是不同的。毗邻建筑结构会使挡风屏的遮蔽效果减弱，地形、地貌使得挡风屏附近流场的涡旋结构增强。

2) 受到毗邻挡风墙背风侧涡旋结构影响，挡风屏挡风墙端位置下行线的遮蔽效果明显优于上行线，而桥梁中段和防风明洞端两线的遮蔽效果相差不大。

3) 来流风速对挡风屏的遮蔽效果影响不大。

4) 风向角增大时，各断面的平均防护系数增大，遮蔽效果增强。

本文仅在无车条件下，进行了挡风屏遮蔽效果的研究。基于既有成果，考虑列车通过时列车气动效应影响下的挡风屏的遮蔽效应，以及列车与挡风屏之间的耦合分析，尚待进一步研究。