离子化程度对硼取代富勒烯C19B n+（n=0-3）体系储氢性能的影响

田传进，赵文燕，李鹏章，汪长安，2，谢志鹏，2，王志刚

（1.景德镇陶瓷大学材料科学与工程学院，景德镇 333403；2.清华大学新型陶瓷与精细工艺国家重点实验室，北京 100084；3.吉林大学原子与分子物理研究所，长春 130012）

1 引言

氢能源被认为是最有前景的清洁能源之一，当前氢的存储和运输仍是制约氢能大规模商业化的瓶颈问题之一，寻找一种安全可行的储氢方式是实现氢能经济的重要保障，人们围绕这一问题已经开展了多年的研究工作［1-6］.在诸多种储氢方法中，固态纳米材料储氢具有质量和体积密度高、安全性能好、便于携带和运输等优点，被认为是一种非常有前景的储氢方式［2，7，8］.此类材料中研究较多的就是质量轻、比表面积大的碳基、硼氮基纳米材料，像碳纳米管、富勒烯、石墨烯、硼球烯、硼氮纳米管等［8-11］.这种储氢方式依靠的是储氢材料对氢气分子的吸附，而这种吸附要满足一定的吸附强度，吸附太弱，储氢量太低，吸附太强，氢的释放动力学不佳，早前研究中已经有人提出最理想的吸附强度为0.2-0.6 eV/H2［12］.

对于纯碳基材料已被证明对氢的吸附太弱，不能满足氢的存储量，而通过碱金属、碱土金属或过渡金属对碳基纳米材料进行化学修饰能够提高氢分子与基底材料间的吸附能［13］.孙等人通过第一性原理计算了氢分子在Li12C60的吸附，预测储氢质量密度可达9 wt%，但是吸附强度较弱，只能考虑低温下使用［14］.Kim等人曾在2006 年指出，通过轻元素取代富勒烯中的碳原子可以提高氢分子在富勒烯表面的吸附强度［12］.氢分子在此类材料表面吸附能的提高，源于掺杂原子向碳原子电荷转移，而氢分子向掺杂原子发生电子转移，使得氢分子以一种准分子的形式吸附在材料表面，也被称为非解离吸附，是一种处于物理吸附与化学吸附之间的吸附状态，这种储氢机制被称为极化吸附机制.由此可见，吸附位点的电荷布居状态是影响吸附能的重要因素.另外，已有的研究还表明，富勒烯离子化可以影响它们结合氢分子的能力，张等人通过第一性原理计算指出富勒烯不论带正电荷还是带负电荷均能提高氢分子的结合强度［15］.离子化体系因所带电荷对氢分子产生极化效应使得氢分子的吸附能增加.由此，则会产生一个问题，离子化化学修饰富勒烯对氢分子的吸附能影响是怎样的？另外，以往研究结果表明B取代富勒烯不但增强了氢分子的吸附强度，而且还会影响氢分子在表面物理吸附到化学吸附转变的能垒高低［16-19］.但是，离子化程度即所带电荷量的多少对吸附能垒是否会有影响，至今还没有过相关的报道.

为此，本文开展了离子化B取代富勒烯所带电荷对氢分子吸附强度影响的第一性原理理论研究工作.我们选择了C19B、C19B+、C19B2+和C19B3+为研究对象，计算了氢分子在其上面的吸附强度.同时计算了氢分子在其表面由非解离吸附到化学吸附的势能面，给出了其由非解离吸附态到化学吸附态的转变过程.

2 计算方法

本文中所计算体系涉及到氢气分子的非解离吸附态，这是一种介于物理吸附态与化学吸附态之间的一种吸附状态，我们采用了包含色散矫正的DFT-D3 方法对其进行结构优化［20］.已有研究表明DFT-D3 方法使用Becke型交换泛函如BLYP或B3LYP可以取得较好的计算结果［21，22］，所以，我们在本研究中采用了B3LYP-D3 方法，这种方法已被证明适合处理氢分子在碳基纳米材料表面的吸附研究［23-25］，计算中采用了分裂价基基组，分别对氢和非氢原子加了p 和d 极化函数，同时对非氢元素加了弥散，记为6-31 +g（d，p）.在优化结构的基础上，为了证明所得到的结构为局域极小点或者为过渡态，在相同的水平下对每个体系做了简谐频率计算.本文的所有计算采用Gaussian 09 程序完成［26］.

氢分子和C19Bn+之间的吸附能通过下式给出：

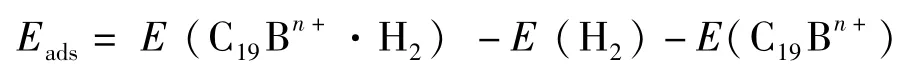
式中E（C19Bn+·H2）为非解离吸附体系的能量，E（H2）和E（C19Bn+）分别是H2和C19Bn+的能量.

3 结果与讨论

计算中采用了全原子优化的方式，首先优化了C19Bn+（n=0-3）体系的结构，并且对每个结构均做了频率计算，得到的频率均为正值，说明得到的结构为局域极小点.为了分析活性位点上的电荷布居情况，C19Bn+（n=0-3）体系进行了Mulliken电荷布居分析.C19Bn+（n=0-3）体系的部分几何参数和B及与B相连的C原子的Mulliken电荷分布在表1 中给出，B原子上所带电荷数随着离子电荷数的增大而增大，由中性体系到正一价再到正二价、正三价，原子C1、C2、C3 和B上的正电荷分布逐渐增多，其中B原子上的电荷分别为1.618、1.787、1.841、1.950.可见，通过不同价态离子可以调控B原子位上的电荷布居，从而我们可以研究B原子位上的电荷量对氢气吸附性能的影响.

为了研究B原子上的电荷布居对氢气吸附性能的影响，在优化得到的C19Bn+（n=0-3）体系的B位点上引入氢分子，通过进一步优化得到了C19Bn+·H2（n=0-3）体系非解离吸附态，接着通过过渡态搜索得到了H-H在表面解离的过渡态结构，进而得到了化学吸附态，所得结构分别如图1 中P、TS及C所示.对得到的每一个结构在相同的水平下对其进行了振动分析，对所有的P态和C态计算得到的所有频率都为正值，说明它们均为局域极小点.而对于TS均有一个绝对值较大的虚频，虚频所对应的振动模式是H-H拉伸振动，其明显对应物理吸附态与化学吸附态间的转换.我们将得到的一些结构的部分几何参数在表2 中给出.

表1 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+（n=0-3）的部分几何参数和部分原子的Mulliken电荷分布.R表示键长，单位：埃.Table 1 The partly geometrical parameters at B3LYP-D3/6-31 +g（d，p）level for C19B n+（n=0-3）system，and the Mulliken charge distribution of some atoms.R is the bond length in angstroms.

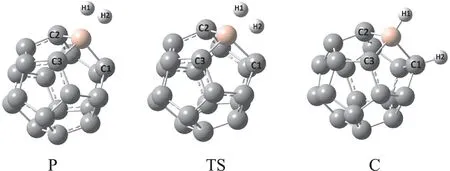
图1 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+·H2的物理吸附态P、过渡态TS、以及化学吸附态C的结构Fig.1 Optimized geometric structures of thephysisorption state（P），chemisorption state（C），and the transition state from Pto C at B3LYP-D3/6-31 +g（d，p）level.

由表2 中可以看出H-H间的键长是随着B原子上的电荷布居数的增多而增加的，B原子上的电荷分布越多，H-H键长增加，由0.745 Å增加到0.823 Å，H-H键的增长也反应了氢分子被极化的程度增加.而B-H间的键长减小，说明随着电荷离子化程度的增大，其对氢气分子吸附逐渐增强.

表2 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+·H2（P）（n=0-3）的部分几何参数，R表示键长，单位为埃.Table 2 The partly geometrical parameters at B3LYP-D3/6-31 +g（d，p）level for C19B n+·H2（P）system.R is the bond length in angstroms.

表3 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+·H2（P）（n=0-3）的部分原子的Mulliken电荷分布Table 3 The Mulliken charge distribution of some atoms at B3LYP-D3/6-31 +g（d，p）level for C19B n+·H2（P）（n=0-3）system.

表3 给出了不同离子化程度体系的非解离吸附态C19Bn+·H2（P）（n=0-3）中部分原子的Mulliken电荷布居.由表3 中数据可以看出体系由中性体系到正一价再到正二价、正三价，H1 原子上的电荷布居分别为0.018、0.153、0.204、0.248，H2 原子上的电荷布居分别为0.015、0.160、0.208、0.248，B原子上的电荷布居比没有吸附氢分子前均变小，明显可以看出氢分子上有电子向B原子发生了电荷转移，而且发生的电荷转移数也是逐渐增多的，也进一步说明了氢分子被极化的程度增加了.

表4给出了C19B·H2、C19B+·H2、C19B2+·H2和C19B3+·H2的各个体系中由非解离吸附态到化学吸附转变过程中相关结构的能量.体系的能量是在B3LYP-D3/6-31 +g（d，p）水平上得到的，记为EB3LYP+D3，同时在相同水平上得到了体系的零点振动能ZPVE（zero point vibration energy），体系的总能量即为EB3LYP+D3和零点振动能之和.由表中数据根据计算方法部分给出的公式Eads=E（C19Bn+·H2）-E（H2）-E（C19Bn+），我们可以计算得到C19B·H2、C19B+·H2、C19B2+·H2和C19B3+·H2体系中氢分子的吸附能分别为：0.053 eV，0.128 eV、0.838 eV和1.553 eV.也就是随着离子化程度的增大，氢分子在其表面的吸附能逐渐增大，这些跟前面分析的电荷布居、电荷转移以及相应几何参数得到的结论相一致.

表4 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+·H2（n=0-3）体系非解离吸附态到化学吸附态势能面上的相关结构的能量.Etotal=EB3LYP+D3+ZPVE.Table 4 The energy of the related structures on the potential energy surface of the transformation from non-dissociative adsorption state to chemisorption state of C19B n+·H2（n=0-3）system at the B3LYP-D3/6-31 +g（d，p）level.Etotal=EB3LYP+D3+ZPVE.

我们将每个体系的化学吸附态能量设为能量零点，根据各体系非解离吸附态到化学吸附态转变过程中涉及的相关体系能量，计算出了非解离附态和过渡态相对于化学吸附态的相对能量，得到了反应势能面（如图2 所示）.从图中可以看出C19B·H2、C19B+·H2、C19B2+·H2和C19B3+·H2体系非解离吸附态到化学吸附态转变的能垒分别为11.16、9.79、10.61、13.24 Kcal/mol.反应能垒出现先减小后增加的趋势，对于开始的减小可能是由于C19B的C1 上有负电荷布居，相对不利于H向上发生电荷转移，而C19B+上C1 电荷布居为正，利于H的电荷转移，从而使得向化学吸附态转变的能垒降低，随着离子电荷数的增加B上的布居数增大，虽然C1 上的正电荷布居数也在增大，但此时B上正电荷布居数增大导致对氢吸附强度的增大使得其向化学吸附态转变的能垒相对增高.由此可见，氢分子在吸附材料上非解离吸附态的动力学稳定性会受到吸附位及周边原子电荷布居的影响.

4 结论

图2 在B3LYP-D3/6-31 +g（d，p）水平上得到的C19B n+·H2的非解离吸附态到化学吸附态转变的势能面.P、C、TS分别表示非解离吸附态、化学吸附态、过渡态Fig.2 Schematic potential energy surface，at B3LYPD3/6-31 +g（d，p）level，for C19B n+·H2from nondisociation state to chemisorption state.P，C，and TS represent non-dissociative adsorption state，chemical adsorption state，and transition state，respectively

基于密度泛函理论并采用包含色散矫正的计算方法计算了氢分子在B取代富勒烯C19B及其离子化体系C19B、C19B+、C19B2+和C19B3+表面的非解离吸附态、化学吸附态、以及由其非解离吸附态到化学吸附态转变的过渡态，得到了其吸附态间转变的势能面.研究结果表明：（1）随着离子化程度的增加，B原子上所带正电荷逐渐增加，当氢分子吸附于B原子位点上时，H-H键长逐渐增大，氢分子被极化的程度逐渐增大，氢分子的在其表面的非解离吸附态的吸附能也逐渐增大，在B3LYP-D3/6-31 +g（d，p）水平下，氢分子在C19B、C19B+、C19B2+和C19B3+表面的吸附能分别为0.053 eV，0.128 eV、0.838 eV和1.553 eV.（2）离子化的B取代富勒烯C19Bn+离对氢分子在其表面的非解离吸附态到化学吸附态转变的能垒有影响，但出现了先减小后增大的趋势.在B3LYP-D3/6-31 +g（d，p）水平下，氢分子在C19B、C19B+、C19B2+和C19B3+表面上由非解离吸附态到化学吸附态转变的能垒分别为11.16、9.79、10.61、13.24 Kcal/mol.可见，我们的研究显示出氢分子在材料表面的吸附能大小及吸附状态的稳定性可以通过调节吸附位点元素的电荷分布来进行调控.