把习题变成问题，让解题走向研究

摘要：人教版初中数学八年级下册《一次函数》一章中没有安排系统研究绝对值函数的内容，却出现了有关绝对值函数的习题。于是，精心设计“一题一课”，从教材中的一道习题出发，引出研究绝对值函数图像和性质的问题（课题），组织学生深度探究以及讨论。相关教学思考有：理解教学内容，从低起点变式生长，放大功能;把握研究路径，基于已有经验组织纠错和优化;精心设计板书，伴随学习过程渐次生成和调整。

关键词：习题讲评问题探究《绝对值函数》结构化板书

习题讲评是数学教学的常规课型。为了达到“思深悟透”的效果，超越习题解答、知识技能巩固的追求，习题讲评不能采取“题海战术”，而宜做到“一题一课”，把一些值得研究的习题变成问题甚至主题，组织学生深度探究以及讨论，从而掌握解决一类习题的通性通法。

笔者最近在江苏省海安市南莫中学（一所农村学校）参加教研活动，注意到人教版初中数学八年级下册《一次函数》一章中没有安排系统研究绝对值函数的内容，却出现了有关绝对值函数的习题。于是，精心设计“一题一课”，从教材中的一道习题出发，引出研究绝对值函数图像和性质的问题（课题），组织学生深度探究以及讨论。虽然课堂上表现得“到处碰壁”“错漏连连”，但是在课后被一些教研专家、名师同行描述为“是一节真实的探究课”。现将该课的教学设计与思考整理出来，以供课例研讨或借鉴。

一、教学设计

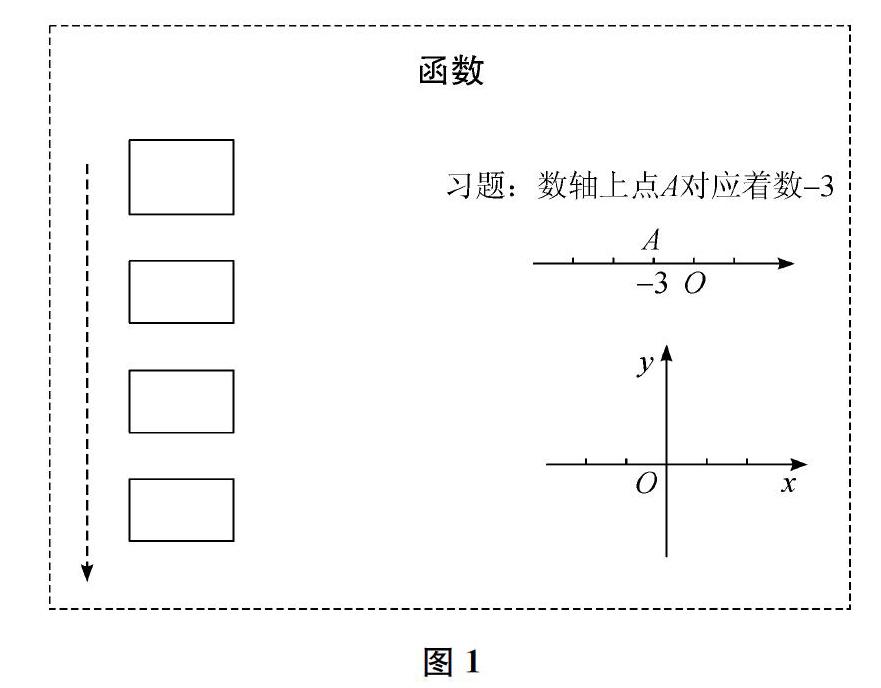
本课不使用课件、投影，也不使用“学案”，只需要传统的黑板。课前，在黑板的主板区板书

（如下页图1所示，旁边留有学生展示区）。另外，为了节约学生课上作函数图像时画平面直角坐标系的时间，让学生提前备好网格纸。

（一）从习题出发，引出课题

习题数轴上的点A对应着数-3，点B对应着数x。

（1）当x=2时，AB=;

（2）当AB=3时，求x的值。

课始，教师先让学生直接回答这道习题，然后预设过渡语：“同学们看到黑板上写着‘函数两个字，但这道习题却是有关七年级的‘有理数加减法的，是老师弄错了吗？”在学生疑惑之际，教师给出变式。

变式数轴上的点A对应着数-3，点B对应着数x。记AB=y，则y与x之间具有函数关系吗？如果有，写出y与x的函数解析式;如果没有，说明理由。

在学生结合函数的概念确认y与x之间存在某种函数关系之后，教师改编呈现习题的原有两问：

（1）当自变量x=2时，函数值y=;

（2）当函数值y=3时，求x的值。

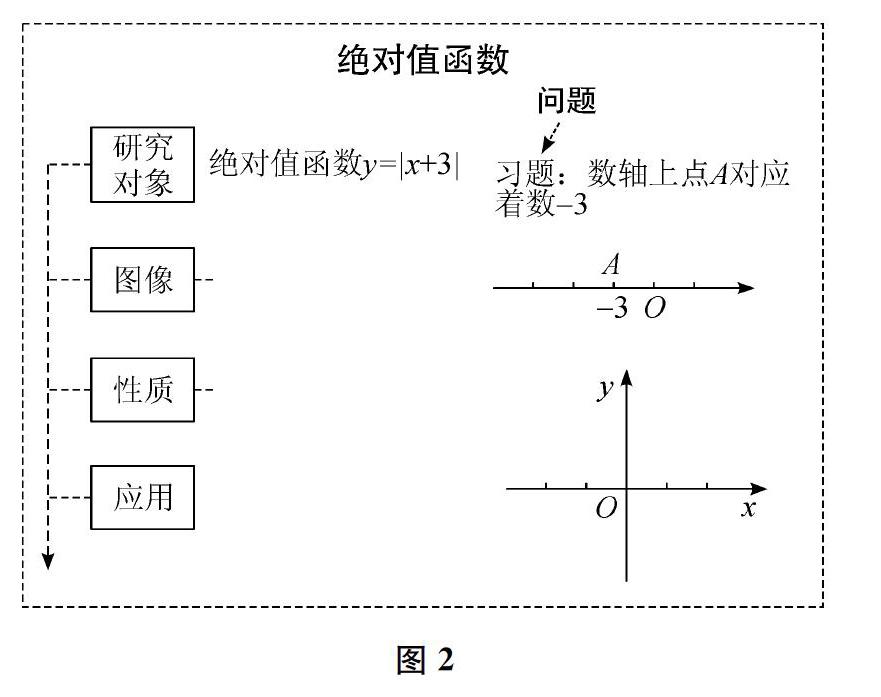
学生会发现这两问与上面的习题是“一样的”。教师顺势指出：“函数只是换了一种工具或角度研究以前熟悉的一些问题。如果只是研究前面的变式问题，则没有什么趣味，因为函数具有更丰富的内涵和更强大的功能。比如，函数y=|x+3|并不是我们熟悉的一次函数，该给它取个什么名称呢？”学生容易想到“绝对值函数”。教师让学生上台补充黑板上的标题，变“函数”为“绝对值函数”。接着，教师提问：“从哪些方面研究绝对值函数呢？”学生由之前学习函数的经验，可以说出“定义、图像、性质、应用”。教师顺势把部分关键词板书在黑板的主板区（如图2所示）——由于不太好定义这类函数，就先写出“研究对象”。

（二）新知探究

问题以y=|x+3|为例，研究这类函数的图像和性质。

教师让学生画图像，在巡视过程中，找出一些不正确的图像，让学生画到黑板上，请其他学生评析、订正和优化。然后，教师安排画图成功的学生分享他们的画图经验，并对那些能结合函数解析式的特点认识图像特征的学生特别表扬。在学生汇报函数图像的特征与函数的性质时，教师做好梳理并有序板书在黑板的主板区。此时，主板区的板书如下页图3所示。

（三）初步应用

例题

（1）利用函数图像解方程|x+3|=2;

（2）利用函数图像解不等式|x+3|>3。

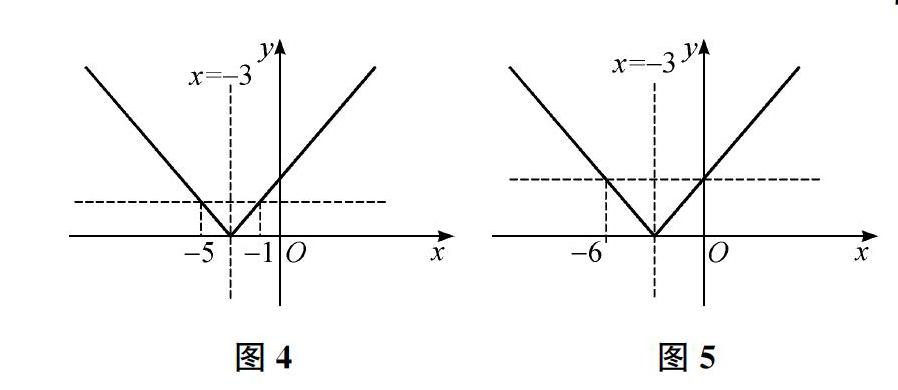
教师先让学生独立练习，然后安排学生

上台演示如下页图4、图5这样的图像分析法，并安排不同的学生再次上台讲解，促进更多的学生运用图像看出方程的解及不等式的解集。

（四）回顾小结，拓展思考

教师引导学生回顾并小结本节课是如何提出问题、怎样研究一类特殊的绝对值函数的，拓展思考课后可以继续研究怎样的绝对值函数，同步完善。最终，主板区的板书如下页图6所示。

最后，基于学生的拓展思考布置两道作业题：

1.画出函数y=|3x-2|、y=|x|-3的图像，描述函数图像的特征或函数的性质（至少3条）。

2.（挑战题）在平面直角坐标系xOy中，点A（x1，y1）、B（x2，y2）在函数y=|x+b|（b为常数）的图像上，若x1y2，借助图像分析b的取值范围。

二、教学思考

（一）理解教学内容，从低起点变式生长，放大功能

本节课的教学内容来源于人教版初中数学八年级下册第19章《一次函数》复习题的第11题：（1）画出函数y=|x-1|的图像;（2）设P（x，0）是x轴上的一个动点，它与x轴上表示-3的点的距离为y，求y关于x的函数解析式，并画出这个函数的图像。笔者充分透析这道题，让它上下勾连、前后贯通，从七年级上册《有理数》一章的“数轴上两点间的距离”这个熟悉的基础问题出发，给学生一个低起点，通过函数视角的变式过渡到“绝对值函数的图像与性质”这个陌生的值得深入探究的问题，放大其教学功能。这样设计的教学过程自然而通透。

（二）把握研究路径，基于已有经验组织纠错和优化

我们知道，面对一个新的数学对象，有一些相对固定的研究路径。以代数对象为例，研究一类新的数时，要研究它的概念界定、相关概念，再研究它的运算法则或运算通性;研究一类新的函数时，要研究它的描述性定义，再从特殊（简单）情况出发，研究它的图像和性质，最后研究它的应用。本节课中，从学生熟悉的一道习题得到一类特殊的绝对值函数，进而组织学生基于已有经验探究这一类函数的图像和性质。这里需要指出的是，八年级学生在探究绝对值函数的图像时，依赖的往往是一次函数的学习经验，从而将绝对值函数的图像“简单化”，比如将其画成一条直线或两条直线。这种典型错漏在学习过程中出现后，教师要将其放大，组織更多的学生参与讨论、纠错和优化。这一过程既是新知识的完善，也可促进学生认识到已有经验的局限性。

（三）精心设计板书，伴随学习过程渐次生成和调整

绝大多数数学课是离不开板书的，而板书设计往往彰显一个数学教师的专业基本功。著名特级教师李庾南善于通过板书将数学知识结构化，她的板书的特点是随着学习过程的展开，内容渐次生成：随时抓取学生的一些关键词句或图形，写在黑板上相应的位置（看似随意的一些内容和布局，其实都来自课前精心的构思）;待到课堂小结时，一个完整、丰富的“结构化板书”就显现全貌，让人眼前一亮，常有惊艳之感。受到李庾南老师板书艺术的影响，笔者在本节课中也精心设计了板书的呈现，包括如何采集、调整和优化的过程，都在上文以板书“分时图”的方式做了呈现，相信会引发一些同行的共鸣。

*本文系江苏省南通市教育科学“十三五”规划课题“基于‘三学理念的初中数学课例研究”（编号：ZX2018007）的阶段性研究成果。

参考文献：

[1] 刘东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起[J].教育研究与评论（课堂观察），2016（11）.

[2] 李庾南，刘东升.好课如诗：富于关联，指向八方[J].中学数学教学参考（中旬），2014（5）.

[3] 刘东升.践行“三学”，渐次生成“结构化板书”——以“分式单元起始课”教学为例[J].中学数学，2018（24）.