磨损计算模型研究现状与发展趋势

赵军

摘 要：材料磨损失效问题普遍存在，磨损造成的经济损失巨大，影响国家工业与经济的发展。磨损计算模型研究有助于预防或控制材料磨损失效，提高机械可靠性，同时对推动摩擦磨损领域的发展有着重大作用。本文对磨损计算模型涉及的材料磨损形式、磨损理论及机理进行分析，并展望了磨损计算模型研究的发展趋势。

关键词：磨损失效;可靠性;磨损计算模型;磨损理论

中图分类号：U455.43文献标识码：A文章编号：1003-5168（2020）35-0065-03

Abstract： The problem of material wear failure is widespread， and the economic loss caused by wear is huge， which affects the development of national industry and economy. The study of wear calculation model helps prevent or control material wear failure， improve mechanical reliability， and at the same time play a major role in promoting the development of friction and wear. This paper analyzed the material wear form， wear theory and mechanism involved in the wear calculation model， and prospected the development trend of wear calculation model research.

Keywords： wear failure;reliability;wear calculation model;wear theory

在摩擦磨损研究领域中，磨损计算模型的发展比较缓慢。据Meng和Ludema[1]统计，过去40多年所发表的5 466篇文献中共包含300多个磨损计算模型，且均难以满足实际应用的要求，其原因并不是缺少对本学科的深入研究，而是由于摩擦磨损研究领域的复杂性和特殊性[2]。从磨损计算模型的发展过程来看，其可以分为三个阶段，即早期的经验磨损计算模型、基于接触力学机理的磨损计算模型、基于材料失效机理的磨损模型，这些模型大都是基于磨损机理特征而建立起来的，但材料在实际磨损过程中并非只有一种磨损机理起作用，而是多种机理共存，相互作用，并可发生转化。因此，对于如此错综复杂的磨损过程，从单一的磨损机理出发建立磨损计算模型，必然存在不完整性。随着现代工业的快速发展，磨损计算模型研究的重要性日益突出，工程上迫切地需要建立一套有效的磨损预测方法来对磨损进行定量研究，以便减小或控制材料的磨损，提高机械可靠性。

近年来，计算机技术、材料学及物理化学等相关学科的发展为磨损计算模型的研究创造了更多的条件，其中以计算机为基础的研究方法得到迅速发展和广泛应用。本文从磨损机理出发对磨损计算模型的建立过程进行分析，并对未来磨损计算模型研究的发展趋势提出了看法。

1 磨损理论的研究与发展

弄清磨损理论和表层材料破坏机理是磨损计算模型建立的基础。按照当今的磨损机理，磨损可以分为磨粒磨损、黏着磨损、疲劳磨损、剥层磨损、能量磨损和腐蚀磨损等。在实际生产中，人们要根据这些磨损形式选用相应的磨损计算模型，对机械零件进行磨损的计算与分析。以下是磨损理论研究过程中建立的几种典型磨损理论，为磨损的理论研究奠定了基础。

1.1 磨粒磨损理论

磨粒磨损主要是磨粒的犁沟作用和微观切削作用，磨粒磨损过程中有尖锐棱角的硬质磨粒被压入摩擦表面，两摩擦表面有相對运动时，该磨粒就像刀具一样对材料表面产生微观切削作用[3]。

1.2 黏着磨损理论

黏着理论认为，摩擦表面的接触实际上是表面上微凸峰间的接触，接触面积小，峰点处于塑性状态，摩擦过程中的瞬时高温使两表面凸峰形成黏结点，滑动过程中黏着点不断地断开和焊接，最终由凸峰接触的黏着效应导致黏着磨损。

1.3 疲劳磨损理论

疲劳磨损理论认为，表面粗糙度和波纹度的存在使摩擦副表面的接触不是连续的，摩擦过程中表面受到周期载荷作用，当应力循环次数达到一定值时，表面就产生疲劳破坏，即疲劳磨损[4]。

1.4 腐蚀磨损理论

简单地说，腐蚀磨损就是金属与环境介质发生化学反应，腐蚀和磨损的交互作用是腐蚀磨损过程中的普遍现象，是机械和腐蚀共同作用的结果。

1.5 剥层磨损理论

摩擦时，硬表面粗糙峰相对软表面滑动，使软表面受到循环载荷的作用，表层内产生剪切塑性变形，形成周期性位错;当剪切变形积累到一定程度时，表层开始出现位错堆积，导致裂纹或空穴的形成，当裂纹长度达到临界值后，就以片状磨削形式脱落[5]。

1.6 能量磨损理论

摩擦过程中，大部分的能量以摩擦热的形式耗散掉，但有9%～16%的能量以势能的形式存储在摩擦副表层材料中，当能量累积到临界值时，材料就会发生塑性流动或形成裂纹，最终脱落，导致材料的磨损。

2 常见磨损计算模型的建立与分类

2.1 磨粒磨损模型

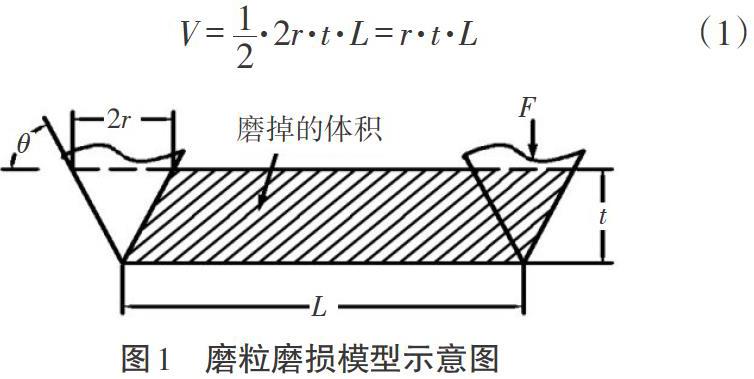
迄今为止，人们已建立了许多磨粒磨损模型，其中以拉宾诺维奇（Rabinowicz）建立的模型为代表，在相关领域得到较多应用。磨粒磨损模型如图1所示，拉宾诺维奇根据磨粒磨损的微切削机理导出磨粒磨损公式。其中，[L]为滑动距离;[F]为磨粒所受载荷;[t]为磨粒压入磨损材料的深度;[θ]为磨粒与磨损面的夹角;[r]为圆锥体磨粒的半径。磨损体积为：

磨粒压入深度[t=r·tanθ]，材料硬度与所受载荷的关系[πr2=FH]，代入式（1），得Rabinowicz方程：

拉宾诺维奇模型的主要不足之处如下：假设所有的磨粒都参加切削，沟内所有的材料都被磨掉，实际上，只有少数磨粒参加切削，沟内也只有部分材料被磨掉;[K]值只考虑了磨粒的形状，而没考虑磨粒大小、硬度等因素的影响;只考虑了材料硬度因素，而没考虑材料其他性能的影响。

2.2 黏着磨损模型

黏着磨损一直作为一种重要的磨损类型，国内外的专家、学者做了大量研究，其中以Archard模型为代表。

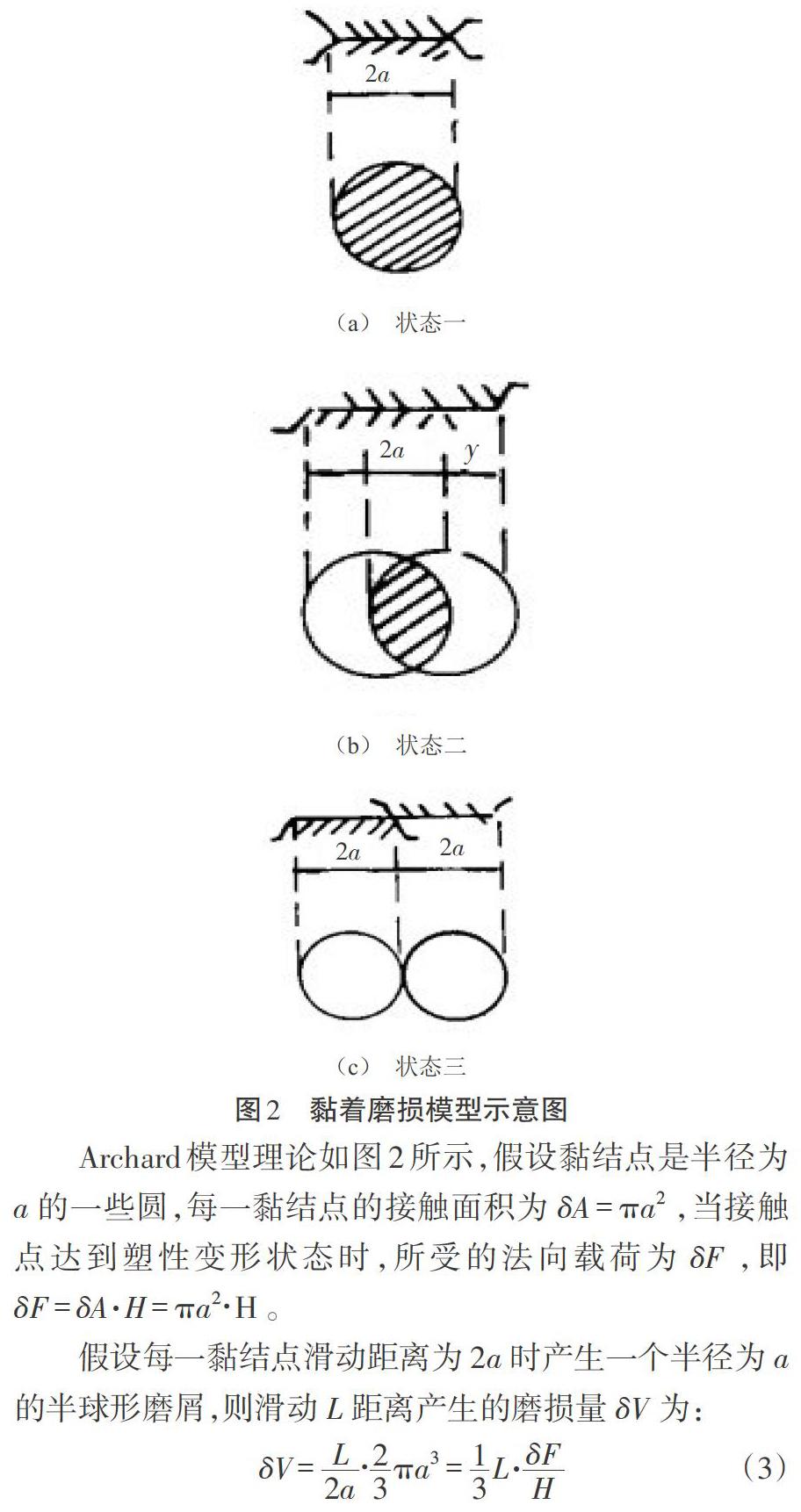
Archard模型理论如图2所示，假设黏结点是半径为[a]的一些圆，每一黏结点的接触面积为[δA=πa2]，当接触点达到塑性变形状态时，所受的法向载荷为[δF]，即[δF=δA·H=πa2?H]。

假设每一黏结点滑动距离为[2a]时产生一个半径为[a]的半球形磨屑，则滑动[L]距离产生的磨损量[δV]为：

滑动过程中总的磨损量[V=δV]，即

Archard模型的不足之处如下：只考虑了材料硬度，而没有考虑材料的其他特性;磨损模型是在一定假设基础上导出的，与实情况不符;不能普遍适用。当磨损的条件发生变化时，该模型就不再适用;磨损系数[K]的确定困难。

尽管Archard模型存在很多不足之处，但仍被认为是磨损研究领域中经典的公式之一，广泛应用。

2.3 疲劳磨损模型

塑性接触情况下的疲劳磨损计算公式如下：

式中，[C]为表征微凸体形状和材料强化的系数（无量纲）;[pa]为名义压力;[t]和[e0]为摩擦疲劳曲线参数;[β=1/（2V+1）]，[V]为支承面曲线的幂近似函数;[Δ]为表面粗糙度参数，[Δ=Rmax/rb12]，其中[Rmax]为轮廓最大高度，[r]为微凸体顶部的曲经半径，[b]为支承面曲线参数（无量纲）;[HB]为材料布氏硬度。

式中，[σT]为材料屈服极限;[f]为摩擦系数。

式（5）考虑了表面微观几何特性、材料物理、机械性能等，同样该公式抛开了磨损机理的本质，难以满足工程实际应用的要求。

2.4 腐蚀磨损模型

腐蚀磨损包括氧化磨损和电化学磨损两大类[6]，其中以Quinn提出的氧化磨损计算模型最为典型：

式中，[W]为磨损率;[a]为微凸峰接触平均半径;[v]为滑动速度;[p]为载荷;[Ac]为阿累尼乌斯常数;[ξ]为氧化膜临界厚度;[f]为氧化物质量分数;[ρ]为氧化膜密度;[R]为普适气体常数;[Qp]为氧化反应的活化能;[T]为微凸峰接触温度。

上述公式中包含的变量多，计算困难，对实际应用没有太大意义，但可以用来分析各变量对磨损率的影响。

3 磨损计算模型的应用及发展趋势

磨损表现出来的统计特性与材料表面性质有着密切的联系，从数理统计角度研究磨损规律，更符合磨损基本特性。近年来，根据数据统计分析方法建立的磨损计算模型得到了大量應用，在一定程度上满足了工程应用的需求，但也存在局限性，需要确定自变量、因变量间的关系，需要大量的试验数据支撑，对数据质量要求也很高，由于磨损的复杂性，有些情况很难直接用函数关系式来描述磨损量。随着科学技术的发展，人们开始用人工智能的方法建立磨损模型，其能够反映样本所蕴含的规律，特别适用于像磨损这样的变量多、关系复杂或尚不明确的系统[5-7]，但该方法建立的模型没有直接的数学表达式，不便于研究各个因素与磨损的关系。

疲劳断裂理论和损伤力学研究的深入以及分子动力学和计算力学的迅速发展为寻求可靠的磨损预测方法和建立精确的磨损模型提供了新的机遇，利用有限元法、分子动力学以及耗散粒子动力学等方法对磨损进行模拟研究是未来磨损研究发展的趋势。另外，在纳米摩擦学的推动下，磨损将进入微尺度研究模式，将在分子、原子的基础上研究材料的磨损性能，从微观结构上建立磨损定律和磨损公式。

4 结论

磨损模型的建立是摩擦磨损研究的重要目标之一，良好的磨损模型可对零件的磨损进行有效预测和精确计算，从而提高机器的可靠性和寿命，直接关系到整个工业世界的经济效益。过去所建立的磨损模型存在很大的缺陷，没有得到实际应用，随着现代先进科技的发展以及对磨损本质的深入认识，如今所建立的磨损模型比以往的精确、合理，并在相关领域得到了应用，但这些模型仍存在一定的局限性，还不能完全满足社会生产的要求。

磨损模型的研究一直以来是磨损研究领域的重点和难点，为此，磨损研究人员必须进行长期的、大量的、系统的研究。鉴于磨损模型研究的重要性和迫切性，本文对磨损计算模型涉及的材料磨损形式、磨损理论及机理进行浅析，并对当前磨损计算模型研究的发展趋势提出了看法，为进一步建立更全面的磨损理论和精确的磨损模型提供参考。

参考文献：

[1]Ludema K C.Mechanism-based modeling of friction and wear[J].Wear，1996（200）：1-7.

[2]李娟，夏建中，孙志礼，等.磨损预测模型试验研究[J].现代制造工程，2011（5）：117-119.

[3]孙伟春.磨粒磨损研究的现状和发展趋势[J].技术创新与应用，2008（2）：71-72.

[4]温诗铸.材料磨损研究的思考与进展[J].摩擦学报，2008（1）：1-5.

[5]Nam P Suh.An overview of the delamination theory of wear[J].Wear，1996（200）：1-7.

[6]H C Meng，K C Ludema.Wear models and predictive equations：their form and content[J].Wear，1995（181）：443-457.

[7]徐流杰，魏世忠.基于BP神经网络对的V9-Cr4-Mo3高速钢冷轧辊磨损模型[J].摩擦学报，2006（6）：541-544.