基于强化学习的平行航班动态定价

方 园，乐美龙

（南京航空航天大学民航学院，江苏 南京 21100）

随着航运市场的不断扩大，各航空公司之间的竞争越来越激烈。 大部分航线会有多家航空公司同时运营，这些具有相同起讫点的航班称为平行航班。价格成为影响其收益的主要因素。航空公司之间的竞争以及供求关系的变化导致航线产品的价值在不断变化，不论是对航空公司还是旅客来说，进行动态定价十分必要。 现有机器学习和大数据技术的发展以及航空市场的宽松环境也为动态定价提供了有利的环境。

原有的较多收益管理都从舱位分配的角度进行研究[1-2]，还有将舱位控制和定价同时进行的[3]，现在逐渐转向从价格的角度进行收益管理。 Gallego G 等[4]最早研究多产品下的动态定价问题，他们将单产品的研究拓展到多产品的动态定价中，采用强度控制的方法求解多产品的动态规划问题，导出相应的Hamilton-Jacobi-Bellman 方程得到渐进最优解。Zhang D 等[5]用马尔可夫决策过程对多个相同目的地之间的可替代航班进行动态定价。 通过上下限和启发式的方法进行求解，并通过定期更新各时点的状态来改变价格。 Akcay Y 等[6]建立了一种能捕捉纵向和横向的产品异质性的线性随机效用框架， 并在此基础上进行多产品联合动态定价，采用微分方程进行求解。 Gallego G 等[7]采用连续时间上的随机博弈，他们利用仿射函数逼近的方法求解微分博弈，并获得渐近均衡解。 曹海娜[8]和朱志愚等[9]采用MNL（multinomial logit model）选择模型对平行航班进行动态定价。 以上这些研究大多采用近似的方法对NP 问题进行求解，使得求解结果不够准确。 目前有部分研究利用强化学习方法解决动态定价问题。 Han W 等[10]通过提前建立其他主体的决策模型并预测他们的价格来构建自身的定价模型，使得问题从多主体决策转变成单主体决策，并采用改进的Q 学习方法求解。王金田等［11］和陆慧[12]根据消费者的选择行为是否易受折扣的影响，将其分为两大类，采用强化学习对双卖家市场进行动态定价，但对消费者选择行为的考虑较为简单。 Rana R 等[13-14]利用带资格迹的强化学习方法分析高峰时刻和非高峰时刻的定价区别，并考虑多个具有关联性产品的定价问题。 通过为其它关联性产品对需求的影响设置参数，问题仍转变为单主体的强化学习问题。文献［15－17］研究智能电网的最优动态定价问题。 通过顾客消费模型构建定价的环境， 同时将动态零售定价问题转化为有限离散马尔可夫决策过程（MDP），并采用Q 学习求解最优定价策略。本文将在以往研究的基础上增加对旅客类型，以及需求在各时间段内的异质性的考虑，并将智能电网相关研究中所采用的单主体动态定价方法拓展至平行航班的多主体动态定价问题中。 相比于以往研究，得到的定价策略更加合理精确，且能有效地捕捉不同类型旅客的选择行为，并有效提升航空公司收益。

1 系统模型

本系统中包含两个重要的角色，分别是旅客和航空公司。 假设两家航空公司各自运营的一个航班为平行航班，且出发时刻较为接近。两个航班的旅客群体设为I。由于航线产品属于易逝品，具有一定长度的销售区间。 在以往的大部分研究中，通过对销售区间进行细分，使得每个时间段至多只有一名旅客到达。 但这种细分方式导致状态非常多，使得实际问题的求解时间大大增加。 另外，在航空公司的实际定价中，也不可能每销售出去一个座位就重新定价，这会使得旅客产生负面情绪。 因此，本文考虑以天为单位，将销售区间分为T 个时间段，每个时间段t 表示一天。通过机票可销售价格的离散化，将其定义为价格集合A。集合的大小是确定且有限的。

在每个时间段t，两家航空公司分别确定该航班的票价，旅客则根据剩余舱位数和当前票价确定自身的购票需求。航空公司的目标是实现自身收益最大化。在销售区间结束后，舱位没有剩余价值。假设系统不考虑超售和团队旅客，且两个平行航班的初始舱位数和各个时间段内的可选择价格都已知。

1.1 旅客行为建模

旅客行为具有两个重要特征，分别是到达率和估值。 假设旅客的到达率λ 服从泊松分布。 此外，还需考虑旅客在两个竞争航班之间的选择行为。 MNL 模型是一个随机效用最大化模型，用来描述旅客在平行航班间的选择。 假设每个旅客购买机票i 后获得的产品效用为：Ui=ui+εi，其中ui=υi+ηfi。 因此，Ui=υi+ηfi+εi，i=1，2。υi表示航班i 的平均价值，η 表示价格反应系数，fi为机票的定价，εi为随机变量， 用来描述不能观测到的效用随机项。 假设εi服从二重指数分布且各变量两两相互独立，将旅客放弃购买航班机票的效用定义为0，则每个旅客的购买概率为

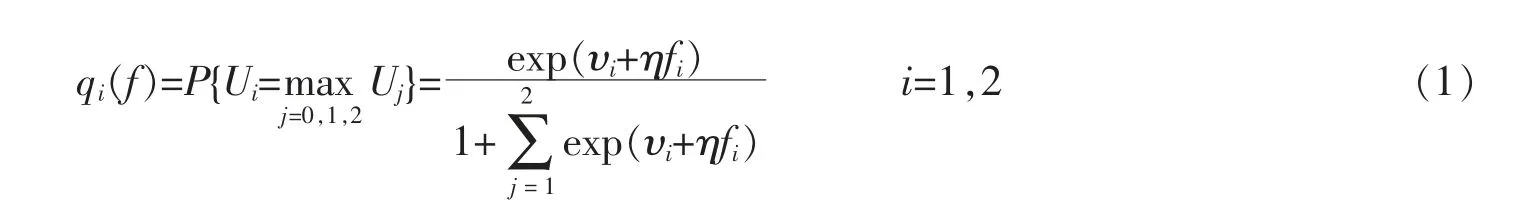
旅客放弃购买任何一个航班机票的概率为

考虑到旅客的策略性行为，短视型旅客在到达的当前时间段，会通过效用模型计算购买概率，若效用值小于0，则会放弃购买；若大于0，则选择购买效用高的航线。 而策略型旅客不止看到当期的效用，还会和未来预期的效用进行比较，这也就造成了计算的复杂性。 但旅客对于未来预期的收益并不能做到完全理性的判断，只是一个自身的经验估计值。 本文利用历史该阶段售价的均值计算未来预期的效用。

1.2 航线产品定价方建模

单航班的动态定价问题通常采用马尔可夫决策过程（MDP）建模。 将单个航空公司的动态定价问题拓展至平行航班的定价问题上，构建多主体的随机博弈Γ。 对一个具有两个玩家和多个状态的随机博弈而言，可以看成是MDP 和矩阵博弈的组合，它是将MDP 拓展至两个Agent 上，也是将矩阵博弈拓展多个状态上。 随机博弈同样具有马尔可夫性质。

航线产品的定价方称为Agent，分别用（i=1，2）表示。 两个航班的座位总数分别用N1，N2表示。xit表示航班i 在时间段t 的剩余舱位数。随机博弈可用元组表示为（S，A1，A2，r1，r2，p，γ）。S 表示状态空间，用当前时间段和两个航班的剩余舱位数表示，st=（t，x1t，x2t）。 在每个时间段内，有旅客到达并且购票，状态会发生变化，时间段t 会减1，两个航班的库存水平的状态也会根据当前时间段售出的舱位数而发生变化。

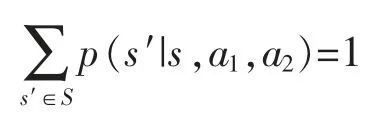
式中：E（rit|π1，π2，s0=s）表示在初始状态s，策略为π1，π2时，在t 时间段的期望收益值。 则Vi（s，a1，a2）为从0开始到结束的总收益。当航班起飞后，不具有剩余价值。因此，最后的收敛条件为：Vi（（x，N，n），π1，π2）=0 或Vi（（x，n，N），π1，π2）=0；Vi（（0，x1，x2），π1，π2）=0。 销售区间结束后，或者当某个航班的舱位全部售出后的收益值为0。 当满足这两个条件之一时，平行航班之间的竞争结束。

每个特定状态的矩阵博弈称为阶段博弈（stage game）。 由于两个航班属于不同航空公司，具有竞争关系，在每个状态下的阶段博弈中寻找纳什均衡策略以实现收益最大化。

定理1 在一个阶段博弈中的纳什均衡可以描述为n 个均衡策略的元组，使得Vi（（s，π1*，…，πi*，…，πN*）≥Vi（（s，π1*，…，πi，…，πN*）for all πi∈∏i。

用Vi*（s）表示纳什均衡策略下的状态值函数，Q*（s，a1，a2）表示在遵循纳什均衡策略下的行动值函数，则

式中：πi*（s，a2）∈PD（Ai）是在玩家i 的纳什均衡策略下在行动ai上的概率分布。T（s，a1，a2，s′）=p（sk+1=s′|sk=s，a1，a2）是在给定状态和联合行动后转移至该状态的概率。

由此，式（5）中的纳什均衡可以重写为

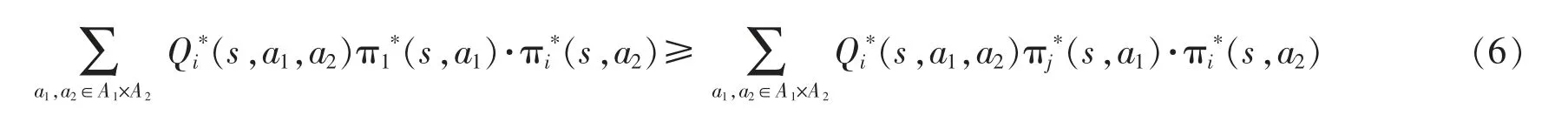
通过在每个阶段博弈中求解纳什均衡，以此作为在每个状态下各Agent 能获得的回报值，根据这个回报值进而学习最优定价策略。

2 算法设计

通过对旅客和航空公司定价方分别建模，利用强化学习算法求解马尔可夫博弈。 强化学习不需要知道环境的具体模型，只依赖获得的奖励学习最优行动，它是多Agent 系统的自然选择。 将旅客的选择行为作为强化学习的环境，每个Agent 通过与环境交互学习最优策略。 在单Agent 的强化学习环境中，环境是相对稳定的。 而多Agent 系统中，环境中还包括其他Agent 的行动和状态，即其他Agent 策略的改变也会影响自身最优策略，因此环境是动态多变的，这对算法的收敛性会带来影响。此外，在单主体的强化学习中，需要存储动作状态Q 值。 而多主体环境中，随着主体的增加，状态空间也增大，联合动作空间呈指数型增长。 因此，多智能体系统的维度非常大，计算也变得更加复杂。 本文通过对时间段和剩余座位数都做了相应的处理以减少状态数。

2.1 环境设置

环境设置的目标是创建一个虚拟的旅客人群，用来模拟在竞争市场中对市场策略的反应，作为强化学习的学习环境。 由于旅客自身的异质性及其购票时的策略行为，将旅客分为4 种类型。 对每种类型的旅客，对其设置到达概率、策略程度和离散选择模型的参数。 具体步骤如下：

1） 根据该时段内各类型旅客的到达率模拟旅客的到达数；

2） 根据旅客的离散选择模型和策略程度确定各类型旅客在该价格下的选择概率，若概率大于0，则选择购买概率高的航班；若概率小于0，则放弃购买。

2.2 Nash-Q 算法

在多主体环境中， 对Q 学习算法进行拓展， 将最优Q 值定义为在Nash 均衡中收到的Q 值， 表示为Nash-Q 值。 计算纳什均衡需要已知自身和对方的收益值和状态值，因此需要维护多个Q 值表。 在每一次阶段博弈中利用Lemke-Howson 算法计算纳什均衡解：（Q1t（st+1，·），…，QMt（st+1，·）），从而计算出在各状态下的各Agent 均衡收益值NashQti（s）。 用这个值对每个Agent 的Q 值进行更新。 Q 值的更新规则为

其中at是学习率，M 为Agent 的个数。 通过这些Q 值的迭代计算，最后收敛至一个稳定值，从而获得最优定价策略。 据此，Nash-Q 算法的流程如下所示：

步骤一：初始化时间段t，初始状态s0，对每个Agent 设置索引i；

步骤二：对所有的s∈S，以及ai∈Ai，初始化Qit（st，a1，…，aM）=0；

步骤三：与旅客环境进行交互，通过Lemke-Howson 算法获得纳什均衡解，确定所有玩家的行动ait后，从而计算收益值rt1，…，rtM并确定下一个状态st+1=s′，对每个i，利用公式（7）更新Q 值；

步骤四：让t=t+1，若t 为最终状态对应的时间段，则结束该循环；否则，返回至步骤三。

其中各个阶段的状态S，做出了相应的简化。状态中xit，不用真实的剩余座位数来表示，而是将一个区间范围内的剩余座位数投射到一个值上以表示当前剩余座位数的状态。 这大大减少计算过程所需的存储空间，也加快了求解速度。

2.3 WoLF-PHC 算法

策略梯度爬升（PHC，policy hill climbing）算法的本质是在混合策略空间中表现出梯度爬升。 PHC 方法不需要知道玩家最近执行行动的信息，以及对手当前策略的信息，这可以减少算法所需的存储空间并且符合实际的竞争环境。 非Agent 选择最高值行动的概率会以学习率δ∈（0，1]增加，因此策略在不断提升。PHC算法能保证在算法中学习的Agent 是理性的，即如果其他玩家的策略收敛至稳定的策略时，那么自身的学习策略也会收敛至对其他玩家策略的最佳反应策略。

WoLF-PHC 算法是PHC 算法的拓展[18]。 它的关键点为：①两个学习率；②采用平均策略来近似均衡策略以确定输赢。WoLF 准则用来修正学习率。算法有两个不同的学习率：δw表示赢时的学习率，δl表示输时的学习率，δl大于δw。 当Agent 输时，学习的要比赢的时候快，这使得当Agent 学习得比期望糟糕时，能对其他Agent 策略的变化适应得更快；当学习得比期望好时，要学得更谨慎。 这也给其他Agent 足够的时间来适应策略的变化。 平均策略旨在取代未知的其他Agent 均衡策略，它和当前策略的不同被用作确定算法赢输的标准。在很多博弈中，平均贪婪策略在实际上是近似均衡策略的，这是均衡发挥作用的驱动机制。WoLF 准则使得PHC 算法在自身博弈中可以收敛至纳什均衡解。 由此， 该算法在保留理性的基础上增加了收敛的性质，使其能收敛至其中的一个纳什均衡解。 收敛性质将从下文的几个典型案例计算来开展。 Agent i 的Q 学习更新规则如下：

据此，设计WoLF-PHC 算法如下所示：

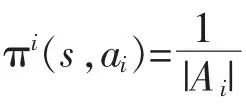
步骤二：对每一次迭代，

1） 在当前状态下基于一个混合探索-利用策略选择行动ac，执行行动后观察收益ri以及下一个状态s′；

C（s）=C（s）+1，

4） 更新πi（s，ai），πi（s，ai）＝πi（s，ai）+Δsai，∀ai∈Ai，其中

步骤三：更新S＝S′，若S 为最终状态，结束该循环；否则，返回至步骤二。

此算法的状态S 所包含的剩余座位数变量的设置同Nash-Q 算法一致。

3 仿真分析

假设两个航班的参数一致。可销售的票价集为{10，15，20，25，30}，总座位数均为50。假设剩余销售期为10 天，对其进行离散化处理，使得每天为一个时间段。 状态包括两个航班的剩余座位数以及当前的时间段。其中，变量xit，将每5 个座位数为一个状态，即将剩余舱位数除以5 取整作为当前的剩余舱位数状态。 对旅客仿真环境中的参数进行设置，建立仿真环境。 参数设置为：ϖ=0.4，φs=0.6，φm=0.6，βLS=0.2，βHS=0.1，不同类型旅客设定不同的λ，υi，η。 Nash-Q 算法中的参数设置为：αi=0.1，γ=0.9。 WoLF-PHC 算法中的参数设置为：αi=0.1，γ=0.9，δ＝0.000 1。

通过案例计算，Nash-Q 算法在5 000 次左右收敛，WoLF-PHC 算法在100 000 次左右收敛，表明两种算法在实际问题中都具有较好的收敛性。 Nash-Q 算法收敛所需的迭代次数要少于WoLF-PHC 算法，但WoLF-PHC 算法的收敛速度明显优于Nash-Q 算法。 这是符合实际情况的，因为Nash-Q 算法在每个阶段中都会计算纳什均衡解，而WoLF-PHC 算法只能利用平均策略来近似策略，这使得其需要更多的迭代后才能收敛。 而也正因为Nash-Q 算法需要在每一次阶段博弈时计算纳什均衡解，这会大大增加求解时间，且该算法需要已知自身和竞争对手双方的Q 值，这对于存储空间的要求也有所增加。因此，WoLF-PHC 算法不论是在求解时间还是耗费的存储空间上都要优于Nash-Q 算法。

表1 是航班在各个时间段的定价。 索引行为距离离港日期的时间，0 为停止售票的时间点。 Strategy 1为旅客的保留价格稳定不变时的定价策略，Strategy 2 为航班在旅客保留价格随时间而变时的定价策略，Strategy 3 和Strategy 4 考虑策略型旅客及保留价格变化的定价策略，且Strategy 4 的旅客策略程度的参数设置的要高于Strategy 3，由此可以看出策略程度对价格制定也会产生一定的影响，使得整体制定的价格都稍低一些。 从整体上看，由于航空旅客到达的特点，机票的价格曲线处于一个增长的趋势。 但由于旅客保留价格的变化及其策略行为使得航空公司需要不断的调整价格，这也就导致价格在增长的过程中会出现一些波动，这些波动能更好地适应旅客行为的变化。将定价策略放到仿真环境中模拟，得到的收益相比于传统方法提升约1.34%。

表1 航班定价策略Tab.1 The pricing strategy of flight tickets 元

4 结论

利用强化学习算法求解平行航班的动态定价问题，发现该算法对多主体的动态定价问题具有较好的适应性，且能在有限步骤内得到收敛，计算时间相比于传统的近似计算方法较短且更加精确。 通过Nash-Q 算法和WoLF-PHC 算法的求解结果比较，发现WoLF-PHC 算法在求解时间上都优于Nash-Q 算法，且Nash-Q 算法在维护Q 值表上耗费的空间较大。此外，WoLF-PHC 算法在不同的旅客环境中，定价策略也会发生相应的变化，能较好地适应旅客环境的变化。由于航空旅客到达策略与其他行业有所不同，高消费的旅客往往到出发前期才会购买机票，而低消费的旅客会早早的选择进行购票，使得航空机票在整体上呈现出增长趋势。 另外，由于旅客的策略性行为，以及保留价格分布的变化，这也使得航空机票在定价过程中会出现一些波动以适应旅客的随机行为。 WoLF-PHC 算法在平行航班的动态定价问题中的表现优于Nash-Q 算法，且得到的定价策略能有效地增加航空公司收益，对航空公司在越来越剧烈的竞争市场中立于不败之地具有重要作用。