基于机器视觉和改进PID的压电柔性机械臂振动控制

马天兵，周 青，杜 菲1，*，刘 健

(1.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；2.安徽理工大学机械工程学院，安徽 淮南 232001; 3. 安徽理工大学矿山智能装备与技术安徽省重点实验室，安徽 淮南 232001)

1 引 言

柔性机械臂在自动装配、精密加工以及航天航空等诸多行业发挥着重要作用，但由于其尺寸大、质量低的结构特点，在工作中会产生较为复杂的颤振，影响其运转精度及使用寿命[1-2]。因此，需要对其振动进行测量与控制。

振动测量常采用压电式的测量方法，Tian[3]根据电缆振动特性，设计了一款基于压电效应的传感器对电缆的振动加速度进行了测量；曹丽曼[4]选择压路机作为振动测量对象，利用压电式加速度传感器对其振动进行了测量。压电测量方法具有一定的精度，但其接触式的测量方式会改变被测结构的动力学特性，且换算过程存在一定的误差。近年来，非接触的机器视觉技术被引入振动测量之中。陈若珠[5]为测量振动台的振动情况，选择视觉法作为测量方案，完成了振动台振动的准确测量；徐超[6]等将视觉测量法运用于大柔性结构的振动测量之中，也取得了较好的测量效果。相关的测振研究对机械臂的振动测量提供了一定的参考。

在振动控制系统中，控制策略是控制的关键[7-8]。PID控制凭借自身原理简单、适应性强等特点，成为目前被广泛应用的基本控制算法，吴金华[9]利用PID算法对半导体的温度进行了控制；郭咏雪[10]将PID控制方法应用于双轴串联的旋转机械的振动问题。相关算法研究均表明了PID控制的普遍适用性和有效性。但PID控制效果的好坏依赖于不同环节参数的选择，PID参数选择方法包括离线参数整定和在线自整定，其中，自整定方法有模糊PID、神经网络PID等。朱瑛[11]将模糊自适应PID运用于飞行器的稳定控制中。龚兰芳[12]利用自适应PID设计了机器人的位姿控制器。自适应PID虽具有较高的适应性，但在控制中易造成控制器超调，且进入稳定状态的时间较久[13-14]。离线整定参数可利用Ziegler-Nichol响应法、Hang提出改进的Z-N临界震荡法以及Cohen-Coon响应曲线方法等，但是参数选取过程较为繁琐，且参数精度不高，控制效果一般。

针对上述问题，本文选择刚柔双关节机械臂作为被控对象，设计基于机器视觉与优化PID的振动控制系统。利用机器视觉技术与图像处理方法对振动位移进行测量，并将测量结果作为系统控制器输入，选择人工鱼群算法对PID参数进行优化选取，控制器输出信号经输出卡转化为控制电压，再由功率放大器放大，控制压电作动片实现振动抑制，最后利用实验验证控制效果。

2 整体方案

基于机器视觉测量与优化PID的柔性机械臂控制系统的具体控制过程及设备连接如图1所示，控制对象为步进电机驱动下的刚柔双关节机械臂，相机采集振动图像传输至PC机，经处理得到振动位移，将位移作为优化PID控制器的输入，并由输出卡输出控制电压，经功率放大器放大，控制柔性臂杆上的压电作动片，实现振动的主动控制。

图1 主动控制系统装置示意图

为实现上述方案，需要首先设计并搭建柔性机械臂振动控制平台；其次设计视觉测振系统并验证其准确性；然后获取机械臂的模态参数，利用人工鱼群算法对PID控制参数进行寻优得到优化后的PID控制器，并仿真验证控制有效性；最后综合利用视觉测振与优化PID进行振动控制实验。

3 控制系统实验平台搭建

双关节刚柔机械臂的柔性臂杆选择300×15×1 mm的不锈钢材料，柔性臂杆末端设置垂直臂杆的标记平面，材料为轻质泡沫片，重量可忽略不计，其上标记点为半径2 mm的黑色实心圆；刚性臂杆选择200×15×6 mm的碳钢材料，设计并加工相关连接关节等部件；根据转矩等信息选择柔性、刚性臂杆驱动电机分别为J-4218HB2403、J-5718HB3401步进电机(下文分别记为大电机、小电机)，并配置相应驱动器和控制器；根据振动特性，选择最高帧速率120帧/s，30万像素，Imaging Source公司生产的DMK 33G618 CCD相机，相机布置于柔性臂杆驱动电机处，并使其视野方向平行于柔性臂杆；压电作动片选择22×19.5 mm的压电陶瓷单晶片，极板面积为18×18 mm，压电常数d31=220×10-12C/N，其两表面极板间距离d=0.2 mm，粘贴位置为臂杆根部；功率放大器选择南京佛能科技有限公司的HVD-300D功率放大器；数据输出卡选择NI公司的USB-6003，其同时具有数据采集和输出功能；根据上文控制系统方案及控制过程进行实验平台的搭建，整体实物如图2所示。

图2 实验平台实物

4 刚柔耦合下的机械臂振动特性分析

柔性机械臂在驱动电机激励下会产生非线性振动，而刚柔臂杆耦合下的振动更为复杂。为探究电机不同转速、细分和频率等设置对其振动的影响，并确定后续控制设置情况，本文选择实验法对其振动特性进行探究。实验中，对系统作出如下前提条件[8]：

(1)仅考虑柔性机械臂转动方向处的振动位移，不考虑其轴向及剪切变形；

(2)忽略重力及阻力等因素对系统的影响。

被研究机械臂的驱动电机为步进电机，其转速由细分、驱动脉冲频率以及步距角共同决定，具体关系为：ω=fqθb/nx，其中，ω为转动角速度，单位为(°)/s；fq为电机驱动脉冲频率，即每秒输出的脉冲数；θb为电机步距角，nx为电机细分数。上述参数量及其可选值较多，导致组合的参数设置组量过大，逐一试验耗时巨大。针对上述情况，拟采用正交试验的方法设计试验方案。

从变量中选择大、小电机的细分数，以及小电机角速度作为待定参数。根据工程实际选取32，64，128作为电机细分的3个水平；选取5(°)/s，10(°)/s，15(°)/s作为小电机角速度的3个水平，并且设定末端总速度为20(°)/s，选择L9正交试验表进行试验方案设计，具体如表1所示。其中，ω1，ω2为大、小电机的角速度，单位为(°)/s；nx1，nx2为大小电机的细分数；fq1、fq1为大小电机驱动脉冲速率，单位为pulse/s。

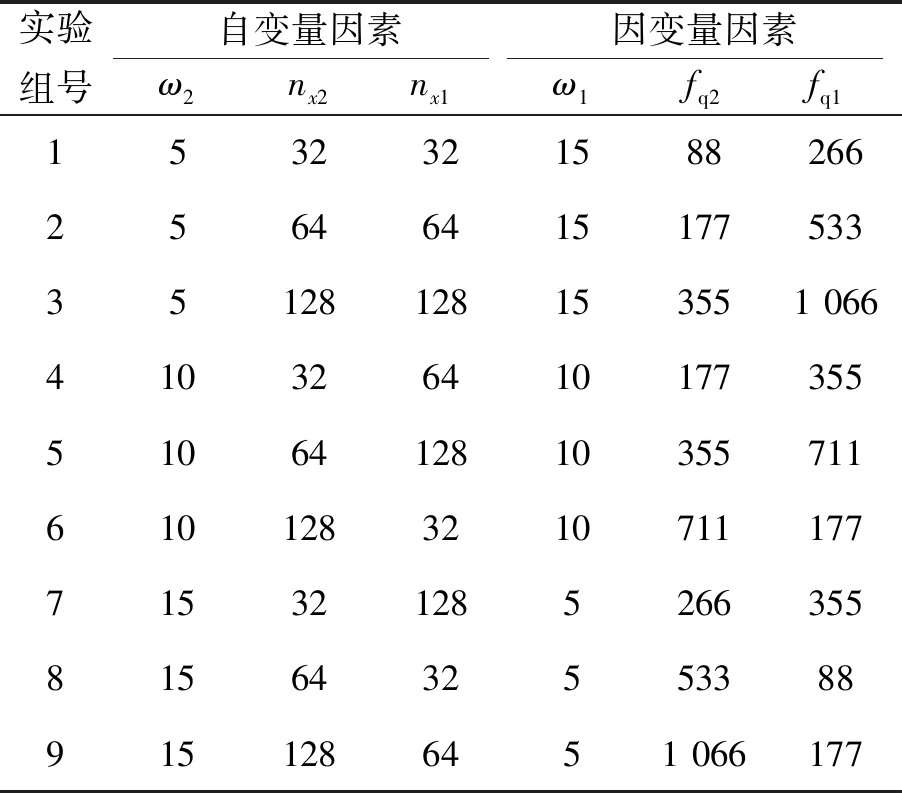
表1 正交试验表

利用实验平台的压电片、采集卡以及PC进行测量，将柔性臂杆转动至刚性臂杆的直线延长线位置，作为初始位置。设定两步进电机转动方向一致；同时启动大小电机，采样时间设为10 s，采样率设为1 k。按照表1参数分别设置并进行9组实验，得到9组原始时域信号。由于电机电源的干扰，需要对原始信号进行去噪，利用Matlab进行低通滤波处理，截止频率选择45 Hz，得到最终结果如图3所示。

从图3可以看出，9组情况下的柔性机械臂振动，均呈现出先大幅值振动然后逐渐衰减至稳定的小幅值振动的趋势。对各组信号进行小波变化和归类分析得，电机转速对进入平稳阶段的时间有一定影响，并且小电机的转速越大、或者大电机的转速越小，振动进入平稳阶段的时间越早。电机细分越小，引起的振动强度就越大，并且大电机细分的影响较大。相比于转速的影响，电机细分对振动强度的影响较大。为体现测量与控制效果，从上述9组实验中选择总体振动幅值最大的3组进行后续研究，即第1、2和4组。

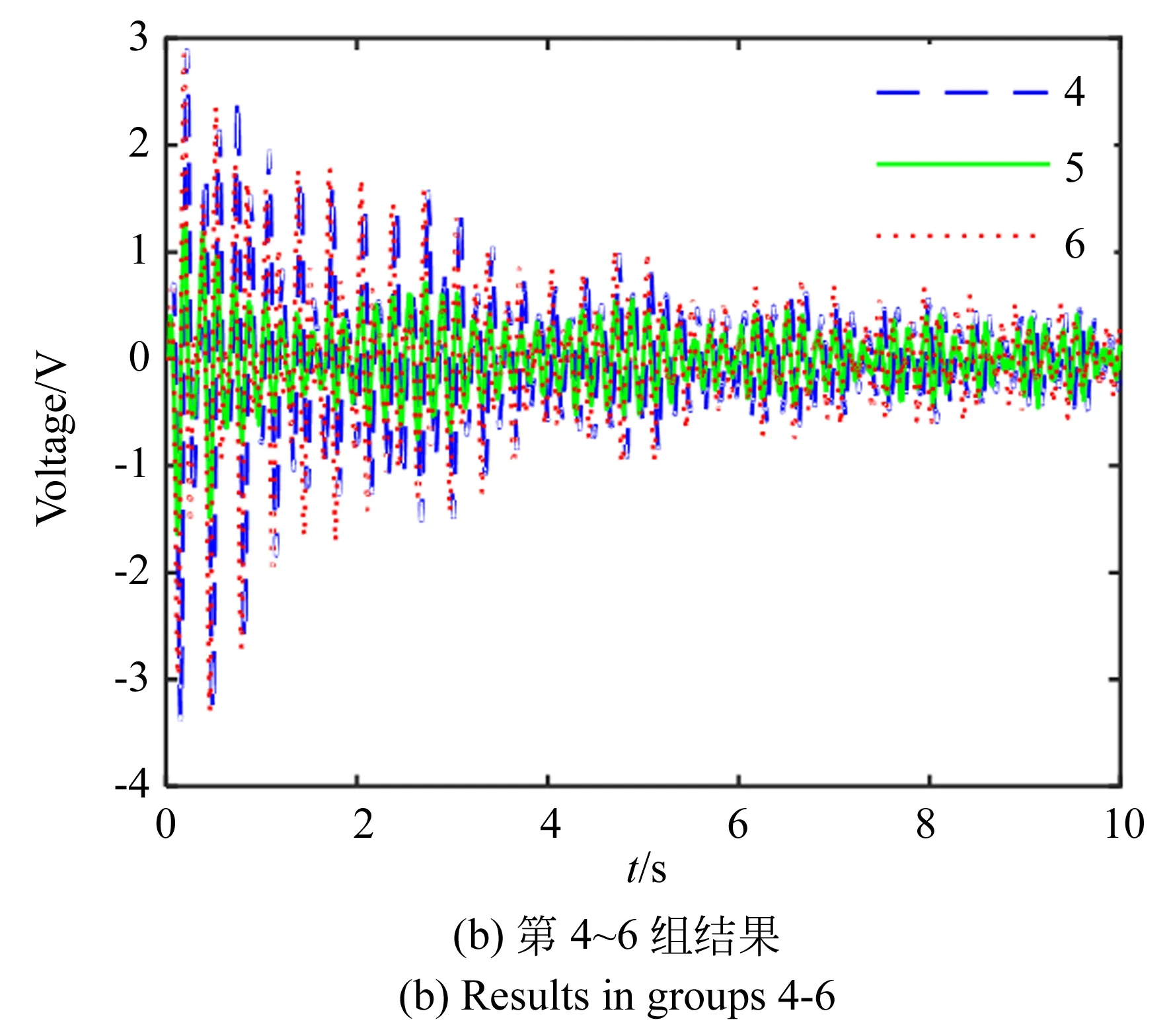
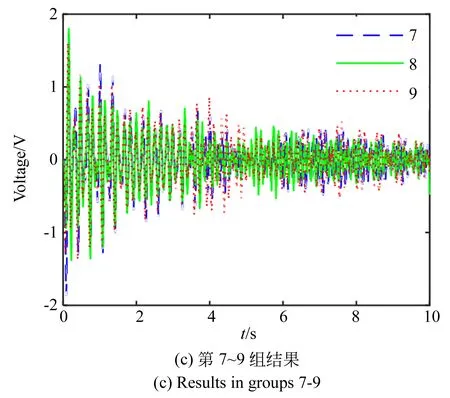
图3 第1～9组测量结果

5 基于机器视觉的测振系统设计

5.1 系统原理及设计过程

视觉测振系统利用相机采集振动图像，并提取图像特征，在不接触被测结构的前提下，完成对柔性机械臂末端振动位移的测量。由于标记点图像特征提取过程较为简单，且精度较高，采集标记点振动图像的测量方式理论上可达到像素级精度，保证测量精度的同时，减少了运算复杂度，避免了后续控制时滞。根据设计方案及采样定理可知，振动测量的最高频率为相机图像采集速率的一半，所以120帧速率的CCD相机最高可完成60 Hz振动信号的采集。

系统软件程序包括采集卡控制和数据处理及图像处理，均在PC端LabVIEW平台上运行，其中，采集卡控制及采集设置利用DAQ助手模块实现；图像处理部分利用Vision模块中的视觉助手程序实现，具体处理过程包括相机的标定、图像滤波、阈值分割以及质心位置确定；编写LabVIEW程序控制两者同时采集、记录数据，并对采集信号进行处理得到振动位移结果。

5.2 测振实验与结果对比

为验证系统测振准确性，并使实验结果具有可对比性。视觉测振的同时，利用粘贴于柔性臂杆根部的压电片进行压电式测量，利用数据输出卡的采集功能，采集并记录测量信号。

设置CCD相机帧速率为90帧/s，采集卡的采样频率同样设置90 Hz，按照表1中1，2和4组参数进行设置，同样采用上节的初始位置，同时启动大小电机，转动10 s后停止，同时采集并记录10 s数据，如图4所示，其中，压电法、视觉发分别表示压电式测量及视觉测量结果。对测量结果进行频谱分析，得到结果如图5所示(考虑篇幅问题，仅展示第1组的结果)。

图4 时域结果对比

图5 频域结果对比

为更具体地对两者测量结果进行对比，定义两者测量差异：

Ec=2|fy-fs|/(fy+fs)，

(1)

其中：fy，fs分别为压电测量方法、视觉测量方法测量结果频域最大峰值的振幅。根据此定义得到3组实验的测量差异分别为1.87%，0.84%和1.93%，平均差异为1.54%。从测量信号特征角度，两种测量方法在误差范围内结果相同，又由于常用压电测量法的可行性，说明了机器视觉方法能实现其振动位移测量，具有一定的可行性。

6 基于人工鱼群优化的PID控制

6.1 算法原理及优化方案

PID是在工业控制中，将被控对象的实时响应与设定目标的误差的比例、积分、微分进行的反馈控制器，控制系统输入e(t)与输出u(t)的关系为：

(2)

式中：Kp表示比例参数，Ti表示积分时间参数，τd表示微分时间参数，均为系统的可调节量。

人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)是李晓磊博士在2002年提出的智能优化算法。鱼往往能自行或尾随其他鱼找到营养物质多的地方，因而鱼生存数目最多的地方一般就是本水域中营养物质最多的地方，人工鱼群算法就是根据这一特点，通过构造人工鱼来模仿鱼群的觅食、聚群及追尾行为，从而实现寻优[15]。

为得到针对柔性臂振动的控制系统中最优的PID控制器，利用上述智能算法对PID控制算法的参数进行最优选取。

具体的优化过程为：

(1)设计PID控制器的柔性机械臂振动仿真系统，其中，PID参数为kP，kI，kD；

(2)将鱼群个体状态以三维向量X=[kP，kI，kD]表示，并初始化每条鱼的状态，设置鱼群数量、认知范围、迭代次数等参数；

(3)将初始鱼群中的个体状态参数作为PID控制参数，并分别进行控制仿真，将控制误差的绝对值之和作为适应度，取最优状态及此状态下的适应度纪录于公告板；

(4)对每条鱼个体进行评估，选择具体行为，包括觅食、聚群、追尾和随机行为；

(5)执行各行为，并更新鱼群中每个鱼个体的状态，形成新状态的鱼群；

(6)将新鱼群中的个体状态参数作为PID控制参数，再次进行控制仿真，利用最优状态及最优适应度更新公告板；

(7)若公告板信息符合要求，或者迭代代数超过设置的最大迭代次数，算法结束，否则再次执行步骤4～7。

6.2 模态参数获取

为了完成PID参数的优化，需要构建柔性双关节机械臂的振动控制仿真系统，系统包括PID控制器、目标函数、状态方程及激励响应，在电机驱动下，柔性臂杆产生振动响应，响应与目标函数的差值作为控制器输入，控制器输出控制柔性臂杆。其中，电机激励下的柔性臂杆响应模型，参考相关文献[16]，利用拉格朗日方程及假定模态法进行建立，并考虑关节柔性进行模型修正，模型中参数采用实验平台参数进行设置，得到模型的电机激励响应结果如图6所示。

图6 电机激励响应

而系统中的柔性臂杆状态方程需要通过实验进行确定，其空间状态方程为：

(3)

其中：X表示振动位移矩阵，u表示输入矩阵，K，M，C分别表示柔性悬臂梁的模态刚度、模态质量和模态阻尼，δ为力因子。

振动控制目标为一阶模态，设一阶模态的刚度、质量、阻尼为k，m，c，查阅相关资料可知，参数满足如下方程：

(4)

其中：ξ为阻尼比，ωn为固有频率。

根据上述公式可知，柔性臂杆的状态方程，可通过结构阻尼比以及固有频率进行求解，而阻尼比以及固有频率，可利用扫频激励实验进行获取。利用上节测振系统，输出0.1～10 Hz的10 s扫频输出信号驱动柔性臂杆上的压电片作动，设置90 Hz的采样率测量其末端位移，结果如图7所示。对结果进行频谱分析，结果如图8所示。

图7 扫频激励响应

图8 响应曲线频谱结果

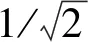
(5)

状态方程中的δM-1中的δ为力因子，此值影响输出比例大小，通过调节输出大小并对比实际响应与仿真结果得到δM-1=0.27。综合上述实验结果及公式(3)，最终得到其空间状态方程为：

(6)

6.3 仿真控制结果对比

根据优化方案进行参数优化及控制仿真，设置人工鱼的感应范围Visual为3，可移动的最大的单位距离Step为0.3，人工鱼数量N=10，迭代最大次数为50，鱼群状态[kp,ki,kd]范围分别为：[(-20,20),(-10,10),(-10,10)]。运行优化算法，得到结果如9所示。

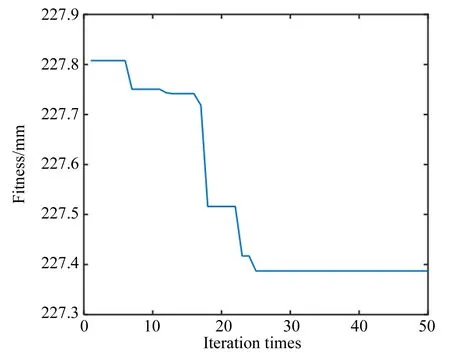
图9 迭代结果

从优化曲线中可以看到，经过50代演算，适应度达到了最优结果71.09，此时，鱼群最优状态为[14.71，7.45，9.56]，利用此PID参数进行振动控制仿真，得到控制效果如图10所示。

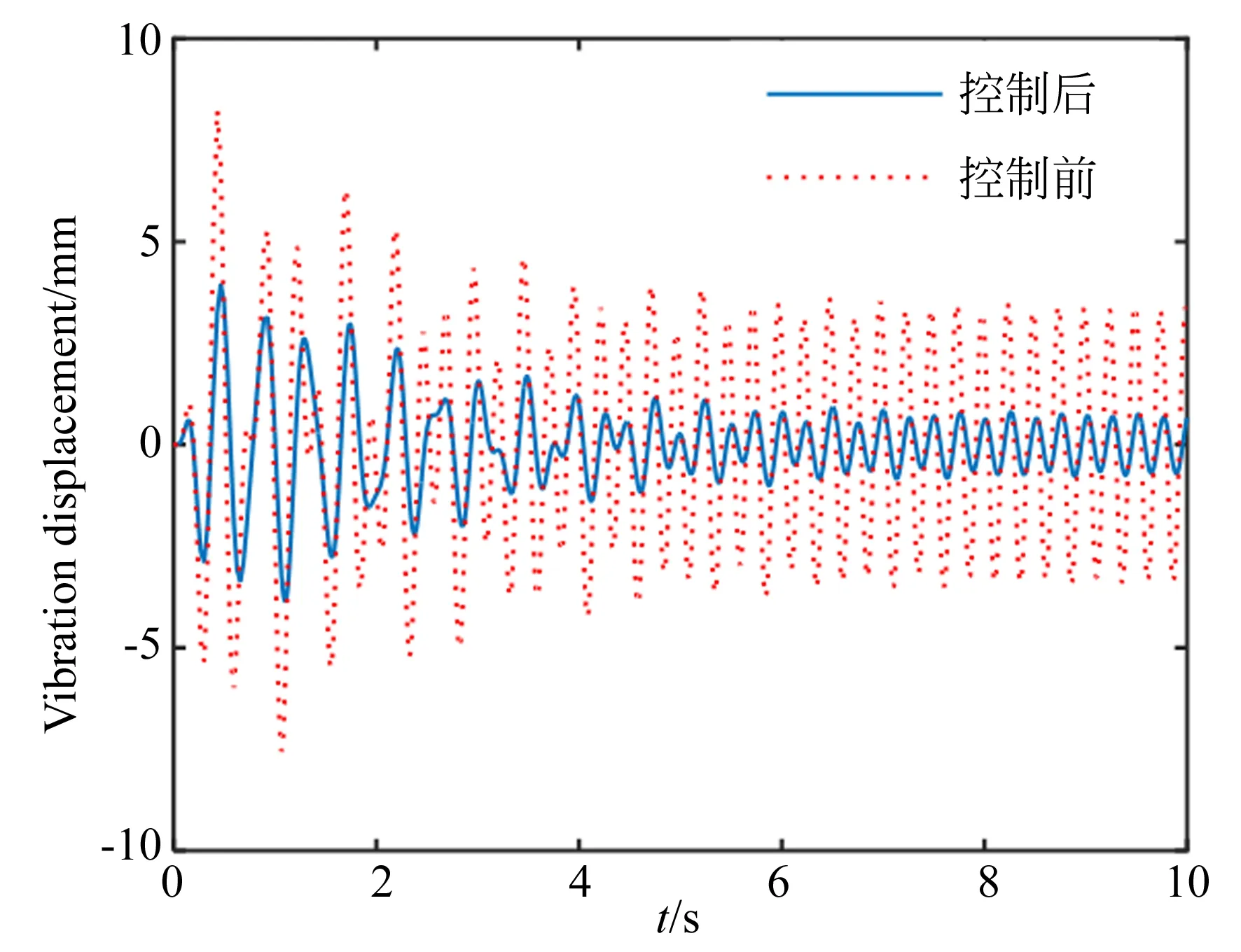
图10 优化参数的仿真实验结果

为进一步说明人工鱼群参数优化法的优越性，选择Ziegler-Nichol响应曲线法(Z-N法)进行参数选取以对比控制效果。

Z-N法是根据阶跃响应曲线信息结合经验公式来整定参数的，经验公式为：

(7)

其中，比例系数K表示阶跃响应稳定后的幅值；滞后时间τ表示震荡前曲线拐点的切线与x轴的交点的横坐标；时间常数T为震荡前曲线拐点的切线纵坐标为K时的横坐标减去纯滞后时间。

仿真系统中得到系统的阶跃响应信号，如图11所示。对其进行处理可知K=0.003 54，τ=1.00，T=0.059。根据公式6可得到PID参数Kp=19.99，Ki=2，Kd=0.5，将Z-N法得到的参数结果作为振动控制参数，仿真结果如图12所示。

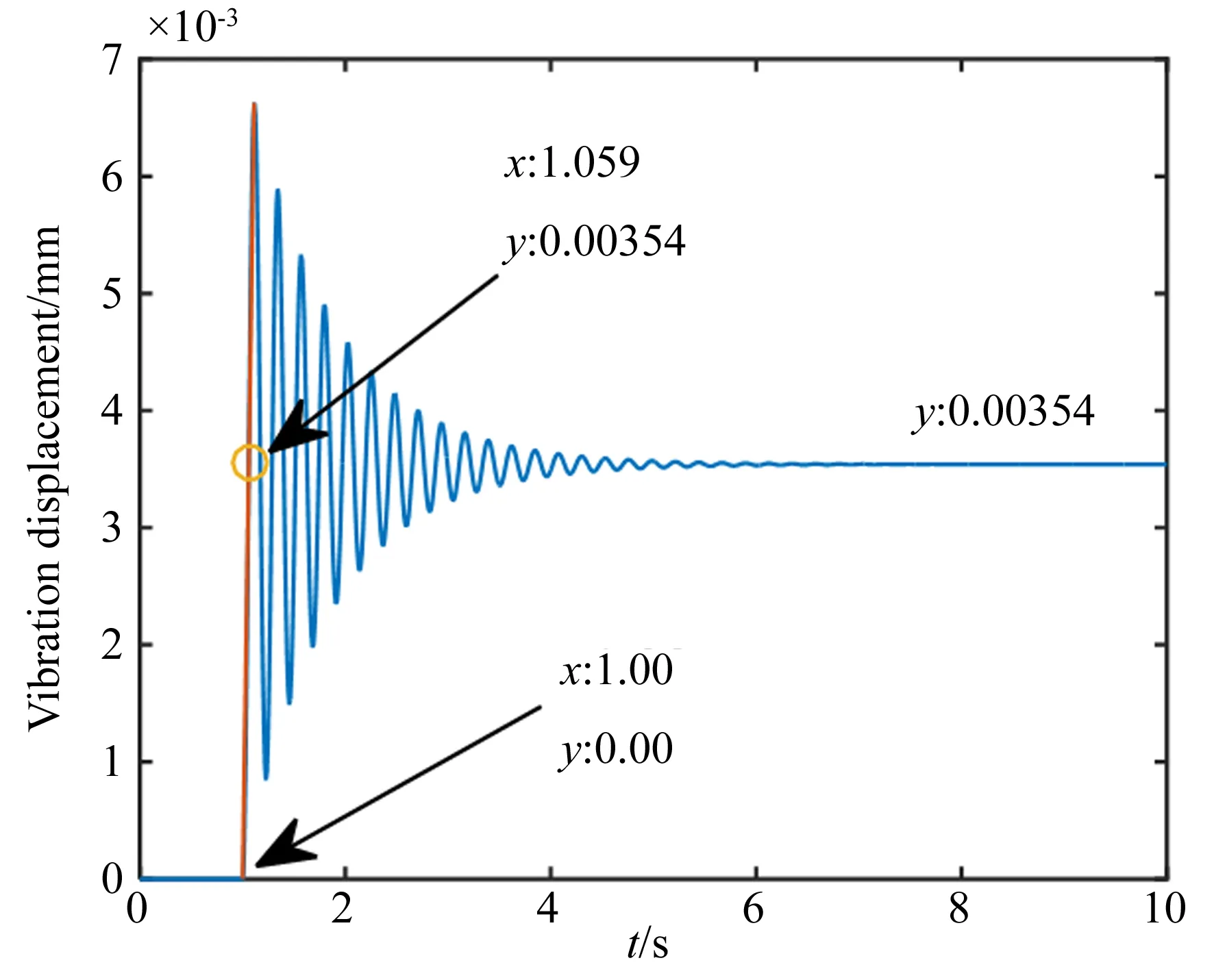
图11 阶跃响应曲线

图12 整定参数的仿真实验结果

根据上述仿真实验结果可知，经过智能算法优化的PID控制方法能够实现振动抑制，并且，相较于Z-N法整定参数，优化参数的控制器仿真控制效果更好，且无需进行繁琐的处理，具有一定的优越性。

7 基于视觉测振及优化PID的振动控制实验

控制程序在上文测振程序上进行扩展，增加输出卡设置以及PID控制模块。按照表1中1，2和4组参数进行电机设置，测振系统采样率设置为90 Hz；数据输出卡为连续输出模式；设定输出范围为-10～10 V。启动电机运行程序，调节功率放大器输出幅值比例大小，运行10 s并纪录相关信号。

为验证控制效果，在无控制、优化参数以及整定参数情况下分别进行实验，并对各实验结果进行频谱分析，结果如图13、14所示(考虑篇幅问题，仅展示第1组的结果)。

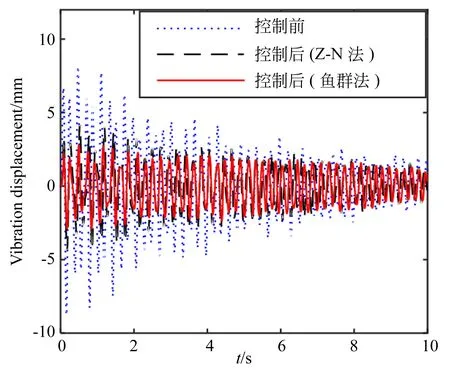
图13 控制前后振动位移对比结果

图14 控制前后频谱对比结果

为进一步说明控制效果，取频谱图中的峰值作为信号强度，控制前后强度变化率作为控制效果，第1、2和4组参数下实验的控制效果及平均值如表2所示。

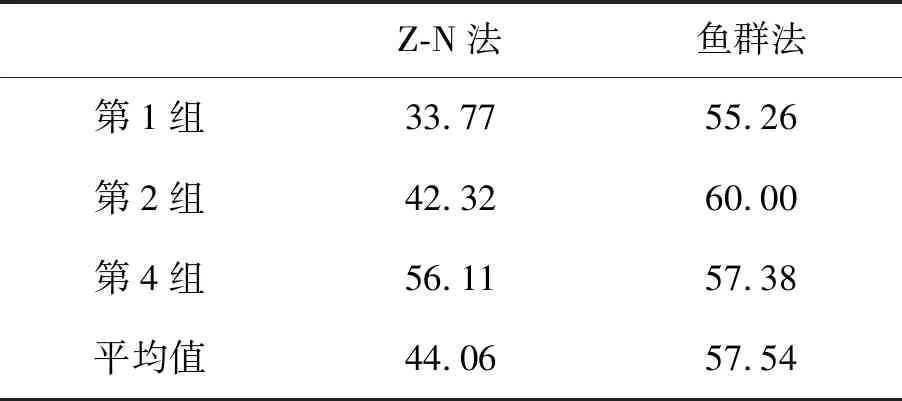
表2 控制效果

综合上述结果可知，两种方法得到的参数均能实现振动位移的控制，从控制时域结果可以看出，两种方法对前几秒起步阶段的振动起到了较好的抑制效果。从频谱分析结果可以看出，Z-N法与鱼群法的平均控制效果分别为44.06%，57.54%，且每组实验中鱼群法的控制效果均有相应的提升。实验结果验证了优化参数后的算法具有较好的振动抑制效果。

8 结 论

文中提出的一种基于机器视觉测振并结合人工鱼群优化PID的柔性机械臂振动控制方法，在振动测量部分，设计机器视觉测振与压电片压电式测振两种方法的比较，并通过测量实验结果的对比，验证了利用机器视觉技术与图像处理方法设计的振动测量系统的可行性与准确性。在振动控制部分，通过控制实验结果可以看出，利用视觉测量方法以及人工鱼群优化的PID算法实现了刚柔双关节机械臂的振动位移控制，并达到了平均57.54%的控制效果，相较于传统整定参数控制器平均44.06%的控制效果，具有一定的优越性。因此，基于人工鱼群优化PID振动控制方法能够很好地实现对柔性机械臂的振动控制，且控制效果可观。