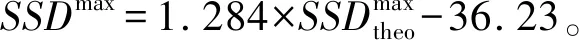基于概率统计的BK7玻璃磨削亚表层损伤深度在线预测技术

吕东喜，陈明达，姚友强，赵 岳，祝颖丹,2*

(1. 中国科学院 宁波材料技术与工程研究所 浙江省机器人与智能制造装备技术重点实验室，浙江 宁波 315201；2. 中国科学院大学 材料与光电研究中心，北京 100049)

1 引 言

硬脆材料的磨粒加工过程通过宏/微观裂纹的成核及扩展，在去除材料的同时不可避免地引起工件的亚表层损伤(Subsurface Damage Depth,SSD)[1-2]。鉴于亚表层裂纹对硬脆材料工件机械和光学性能的负面影响，需要在后续加工过程中通过优化工艺参数逐步降低工件的亚表层裂纹深度，其前提是对工件SSD深度的准确、快速预测，以缩短后续加工时间，提高加工效率。

为了快速准确地预测工件的SSD深度，人们提出了大量基于磨粒粒度[3-4]及工件表面粗糙度[5-7]的亚表层裂纹扩展深度预测方法，极大地方便了光学零件的加工。然而，基于磨粒粒度的预测技术精度十分有限，预测结果甚至相差数倍，难以实现对裂纹深度的精确评估[8]。为了提高预测精度，人们提出了基于表面粗糙度的SSD深度预测方法。Li等人[6]基于压痕断裂力学理论，综合考虑弹/塑应力场对中位裂纹扩展的促进作用，建立了表面粗糙度与亚表面裂纹深度之间的非线性关系模型，实现了对工件SSD深度的预测。LV等人[7]分析了磨粒压痕过程中侧向裂纹成核深度和中位裂纹扩展长度之间的内在关联，建立了基于工件表面粗糙度(p-v值)的快速、准确、无损预测亚表层裂纹深度的理论模型。

虽然基于表面粗糙度的SSD深度预测技术精度较高，但是该类方法并不能对工件的亚表层裂纹深度进行在线预测。为此，Wang等人[9]分析了单磨粒压痕力与中位裂纹深度的内在关联，结合对刀具端面磨粒数目的统计分析，建立了刀具切削力与亚表层裂纹深度之间的非线性关系模型，实现了对旋转超声加工过程中SSD深度的在线预测。该理论模型假设刀具端面上的磨粒具有相同的高度，且均参与亚表层裂纹的形成。然而实际参与切削的磨粒仅占刀具端面磨粒数目的很少一部分[10]，并且参与切削的磨粒尺寸明显不同，导致单个磨粒的切削深度存在较大差异，并最终影响亚表层裂纹的扩展深度。

本文首先基于硬脆材料的压痕断裂力学理论，研究单个磨粒压痕深度与中位裂纹扩展长度之间的内在关联；随后利用概率统计法对刀具端面边缘的磨粒数目进行分析，建立了刀具切削力与单个磨粒切削深度之间的理论关系模型；在此基础上，提出了快速、准确、在线预测工件SSD深度的方法，并结合BK7玻璃的磨削实验进行了验证。

2 单磨粒压痕深度与中位裂纹扩展长度的映射关系

从材料去除机理角度而言，硬脆材料的磨削加工过程可以简化为大量尖锐压头对工件加工面的随机性印压过程[11]。因此可以借助于压痕断裂力学理论，研究实际磨削加工过程中亚表层裂纹的形成机理，如1(a)所示。在磨粒-工件的相互挤压作用下，材料内部会形成复杂的弹/塑性应力场，并产生两种基本的裂纹构型[12]。侧向裂纹成核于塑性变形区域的底部，并沿平行于加工面的方向横向扩展，当延伸至工件的自由面时，实现材料的脆性断裂去除。 而中位裂纹同样成核于塑性变形区域底部，并沿垂直于加工面方向向下扩展，最终形成工件的亚表层损伤(见图1(a))。

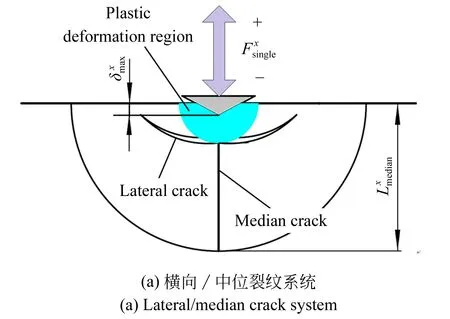
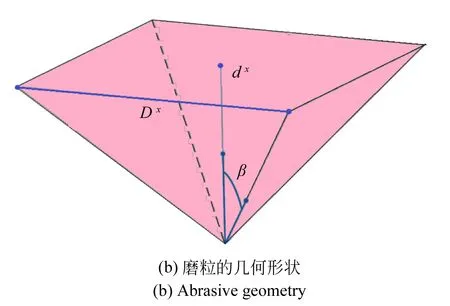
图1 单磨粒印压作用诱发的裂纹系统

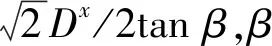
(1)

其中HV为材料的维氏硬度。

(2)

其中：q=0.5，为无量纲常数；αk=0.027+0.090×(q-1/3)；E和KIC分别为材料的弹性模量和断裂韧性。

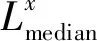
(3)

3 刀具端面边缘磨粒数目的统计分析

3.1 刀具端面边缘的磨粒数目

现有的SSD深度预测方法假设刀具端面上所有的磨粒均参与材料去除[6]，然而对刀具磨损形貌的显微观察表明，只有端面边缘的磨粒参与了材料去除[15]。磨削加工过程及刀具端面上磨粒的分布特征如图2所示。

为了准确获得参与切削的磨粒数目，LV等人分析了磨粒的平均间距b与其进给量之间的关系，并指出只有距离端面边缘小于b范围内的磨粒才有可能参与实际加工[7]，并推导出端面边缘磨粒数目Nall的计算公式：

(4)

需要特别指出的是，在实际磨削加工过程中，参加切削的磨粒数目不仅取决于磨粒的尺寸，还与刀具的切削深度密切相关，即有效磨粒数目仅为刀具端面边缘磨粒数目Nall的一部分。

图2 磨削加工过程示意图及磨粒分布

3.2 磨粒高度的高斯分布特征

Hou等人借助于光学显微镜对刀具表面磨粒的高度dx进行了统计分析，发现最大高度为dmax和最小高度为dmin磨粒的数目都非常少，而平均高度的磨粒最多，并且磨粒高度在一定范围内服从高斯分布[10](见图3)，其分布函数为：

(5)

式中：x为随机变量；y为随机变量x的方差。

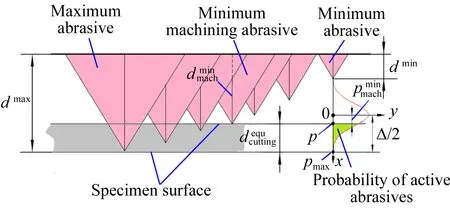
图3 磨粒高度的高斯分布特征

显然，磨粒高度的概率方程P(p)为图3中绿色区域的面积(彩图见期刊电子版)，其值可以通过对式(5)从p到+进行积分获得：

(6)

4 SSD深度预测模型的建立

4.1 刀具切削力和磨粒切削深度的内在关联

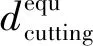
(7)

(8)

(9)

式中：Δ为最大磨粒高度dmax与最小磨粒高度dmin的差值，即Δ=dmax-dmin。

(10)

(11)

在这种情况下，所有参与切削的磨粒的合力可以近似认为是刀具的切削力F，其值可通过对式(11)进行积分获得：

(12)

(13)

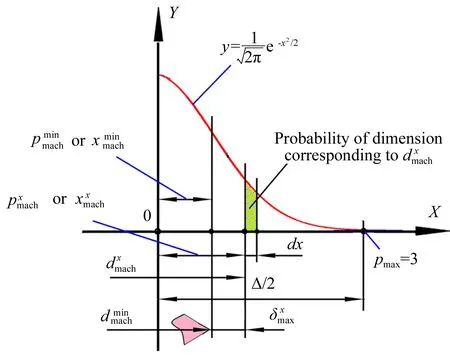
图4 高度为磨粒的分布概率

将式(1)和式(4)带入式(12)，可得刀具的切削力F与单个磨粒切削深度δx的理论关系模型：

(14)

(15)

将式(15)带入式(14)可得刀具的切削力为：

(16)

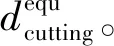
4.2 基于刀具切削力的SSD深度在线预测方法

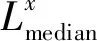
(17)

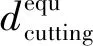
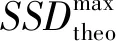
(18)

其中：ξ为比例系数，j为定值。ξ和j可以通过拟合一系列的实验数据获得，其值与工艺参数无关。因此，在已经ξ和j的基础上，结合式(16)～式(18)可以实现对实际磨削加工过程中工件亚表层裂纹深度的在线预测。需要特别指出的是，本研究假设脆性断裂为唯一的材料去除方式，因此上述方法并不适用于预测材料在延性和半延性去除过程中引起的SSD深度。

5 实 验

5.1 实验条件

Wang等人使用金刚石刀具在德国德玛吉公司生产的Sauer Ultrasonic 50 数控加工中心上进行了普通磨削加工实验，详细的实验参数如表1所示[9]。实验过程中，采用瑞士Kistler公司的9256C2型测力仪对磨削过程中的切削力进行了检测。

表1 磨削实验的加工参数[9]

表2 BK7玻璃的材料属性[9]

5.2 实验结果与分析

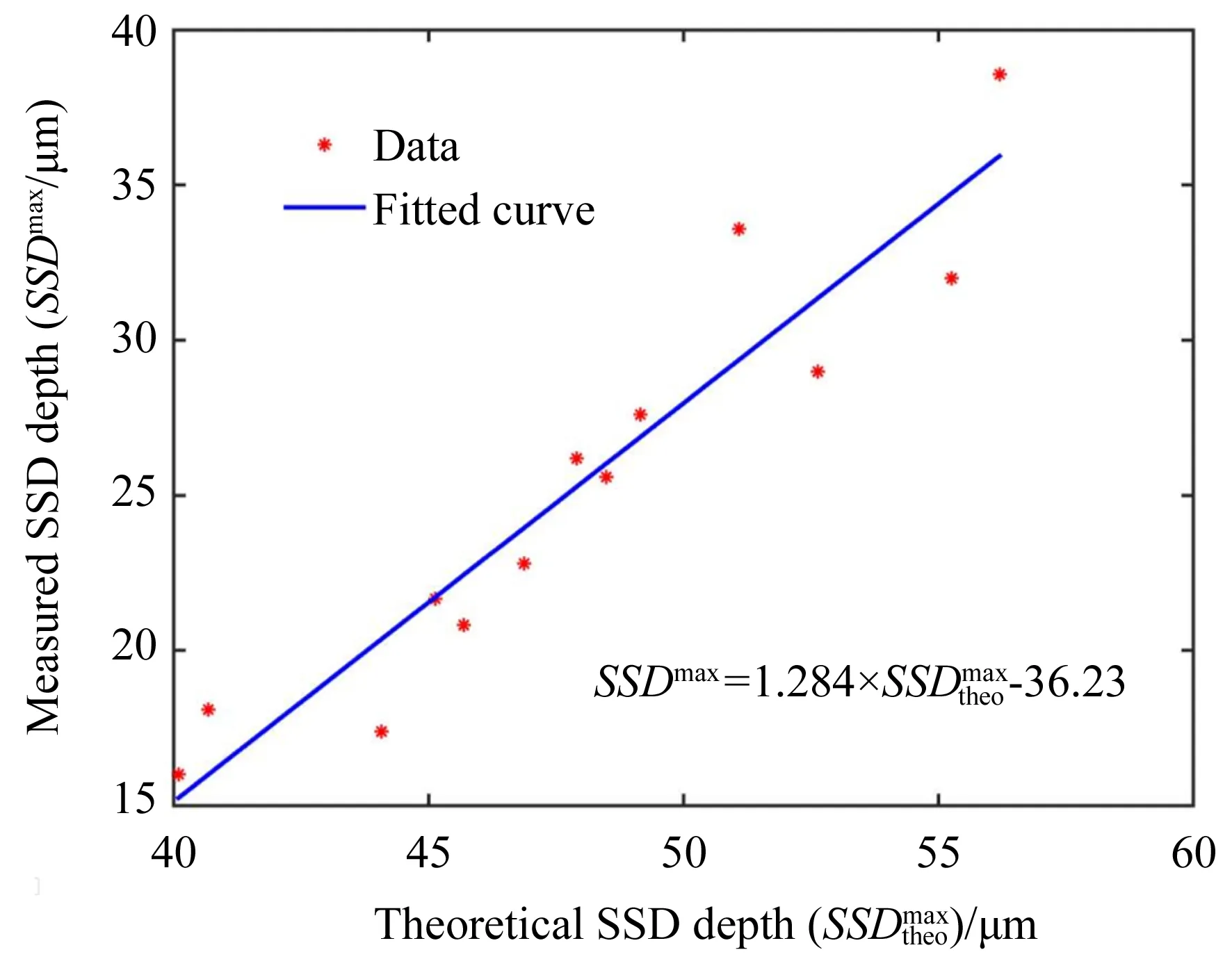
图和SSDmax之间的关系曲线

6 结 论