低渗透油藏气水相对渗透率计算方法研究

赵振峰，唐梅荣，王成旺，魏建光

相对渗透率曲线是正确认识和合理开发油气藏的基础，也是油气藏开发动态计算和预测分析的重要依据之一[1]。致密气藏由于其孔隙结构较常规储层更为复杂，渗透率和孔隙度极低，孔喉细小，孔喉迂曲度很大，流体（气和水）在储层中的渗流较常规油气藏更为复杂。因此，流体在致密储层中的渗流规律和特征也会和常规油气藏有很大区别[2⁃4]。在目前的相对渗透率测定中，主要包括了稳态法和非稳态法两种测试方法。稳态法测试相对渗透率实验结果处理方便，但其实验过程较为复杂，稳定时间长，特别是对于低渗或致密岩芯来说，用稳态法很难得到理想的结果。非稳态法在测试低渗/超低渗岩芯的相对渗透率中有着天然的优势，目前绝大多数低渗岩芯的相对渗透率都是用非稳态法进行测试得到的。但非稳态法测试的实验数据处理较为复杂，普遍采用的是行业标准中给出的JBN方法[5⁃8]。

和常规油气藏不同，致密气藏中流体的渗流并不符合经典的达西定律，而是存在启动压力梯度。同时，致密气藏岩芯还存在一定程度的应力敏感现象[9⁃10]。动态启动压力梯度和应力敏感的存在都会对致密储层中流体的渗流造成影响。而传统的JBN方法并未将这两个因素考虑在内，势必会造成在计算致密储层的相对渗透率时的误差。本文在对致密储层启动压力梯度和应力敏感特征研究的基础上，结合了低渗透储层非线性渗流理论，建立了考虑动态启动压力梯度和应力敏感的致密气藏两相渗流计算方法。

1 动态启动压力梯度

对于致密储层来说，其低孔低渗的储层特征使储层流体（油、气、水）的渗流规律同中、高渗储层中流体的渗流规律存在很大差别，最明显的差别就是流体在致密储层中会呈现非线性渗流特征，并存在启动压力梯度[11]。

目前常规的观点认为对于某一特定岩芯来说，其启动压力梯度是一固定值，绝大部分的其他研究也都是基于这一理论进行的。然而，丁景辰等[12]的研究表明，一方面，岩芯中绝对孔隙压力的大小会对启动压力梯度造成影响；另一方面，由于孔隙压力变化导致的渗透率变化也会对启动压力梯度的大小造成影响，并提出了动态启动压力梯度的概念：在致密气藏的开发过程中，其启动压力梯度并非一成不变，而是一个随着储层压力降低而逐渐增大的动态变化过程，并给出了致密气藏启动压力梯度的预测模型公式：

式中，a为和岩芯初始渗透率有关的系数，MPa·cm-1；λ为启动压力梯度敏感系数，cm-1；Pf为储层孔隙压力，MPa。

根据目标区块岩芯的实际情况进行实验，可以得到式（1）中a和λ的值，进而得到目标区块岩芯中水相和气相的动态启动压力梯度数据。相对于固定启动压力梯度来说，使用动态启动压力梯度能够更准确的表征储层的非线性、非稳态渗流特征，具有更好的参考价值。

2 模型建立

假设致密岩芯均质，气相和水相互不混溶，在同一时刻岩芯横截面上流体的流速一致，同时忽略重力和毛管力的影响，则致密岩芯中水、气的连续性方程分别可以表述为：

式中，vw和vg分别为岩芯水相和气相的渗流速度；Sw和Sg分别为岩芯水相和气相的饱和度；φ为实验岩芯的气测孔隙度。

假设水相和气相的启动压力梯度分别为Gw和Gg，则气、水两相的运动方程可以表述为：

式中，ag和aw分别为和岩芯初始渗透率有关的系数，MPa·cm-1；λg和 λw分别为气相和水相的启动压力梯度敏感系数，cm-1，-P为实验过程中岩芯所受的平均流体压力，MPa；P为流体压力，MPa。

考虑实验岩芯的应力敏感效应[13⁃14]，则：

式中，K为实验有效压差下的岩芯绝对渗透率；Krw和Krg分别为岩芯水相和气相的相对渗透率；μw和μg分别为岩芯水相和气相的黏度；pi为原始地层压力，MPa。

岩芯中水的分流率（含水率）为：

分离变量积分可得到等饱和度面移动方程：

其中，x为某一确定的饱和度在t时刻到达的位置（0时刻原始油水界面在0位置处）。

由式(10)可得：

式中，L为岩芯长度；f′w2为岩芯出口端含水率对含水饱和度的导数。

岩芯两端压差：

式中，veg为初始流速，ΔPeg为初始压差。

将式（5）、（11）、（13）代入式（12）并整理：

以上是考虑动态启动压力梯度和应力敏感的致密气藏气⁃水两相相对渗透率计算模型。

新模型是在常规JBN方法的基础上改进而来，因此和JBN方法一样，适用于所有非稳态法相对渗透率测试实验数据的处理。同时，由于新模型考虑了致密储层的动态启动压力梯度效应和应力敏感效应，因此特别是在致密岩心的相对渗透率实验数据处理方面，采用新模型计算优势更加明显，较常规的JBN方法更为准确。

3 模型验证

以大牛地致密气藏的两块天然岩芯为例，将两块岩芯在气藏条件下（围压模拟上覆地层压力62 MPa，初始流压为原始地层压力26 MPa，温度模拟储层温度70℃）的气驱水相对渗透率实验数据进行整理，分别按照常规JBN方法和本文中推导出的考虑动态启动压力梯度和应力敏感性的气水两相渗流计算方法进行计算。其中，岩芯的气相和水相动态启动压力梯度根据文献[12]中的实验评价方法得到，岩芯在实验条件下的应力敏感渗透率按照文献[13]中的实验方法得到。实验岩芯的具体参数见表1。同时为了验证新方法的准确性，采用毛管压力曲线法[16⁃17]进行验证计算和对比。

表1 实验岩芯参数Table 1 Experimental core parameters

将计算得到的动态启动压力梯度数据和应力敏感渗透率值带入本文所建模型中，并将出口端的产气量进行实验压力下的体积校正，计算产气量和产液量及注入倍数，随后根据公式计算含水饱和度和注入能力比，最终根据式(20)、(21)可以得到新方法下的两相相对渗透率。分别用三种方法计算得到的岩芯的相对渗透率曲线如图1所示。

图1 相对渗透率曲线对比Fig.1 Comparison of relative permeability curve

从图1可以看出，在考虑启动压力梯度和应力敏感性的情况下，本文方法得到的气⁃水相对渗透率曲线和常规不考虑这两个因素的方法（JBN方法）计算得到的曲线特征有明显的不同：在考虑启动压力梯度和应力敏感性的情况下，气、水两相的渗流能力均有明显下降，两相共渗区域范围变窄，其中水相相对渗透率降低速度加快，而气相相对渗透率上升速度有所减缓，等渗点相对渗透率降低，实验结束时，岩芯的残余水饱和度升高，且残余水饱和度下的气相相对渗透率有所降低。这是因为由于启动压力梯度和应力敏感性的存在，对致密岩芯中流体的流动产生了很大的影响，使岩芯中流体的渗流变得更加困难，总体渗流能力下降。

同时和JBN方法得到的相渗曲线相比，本文方法得到的曲线明显和毛管压力曲线法得到的曲线更为一致。为了更好地说明本文中新的两相渗流计算方法的准确性，在上述实验的基础上，选择了18块渗透率范围（0.03～1.15）×10-3μm的天然岩芯，在上文中所述实验条件下开展相对渗透率测试，并分别采用常规JBN方法和本文所述新方法进行相对渗透率计算，将其计算结果和相同岩芯采用毛管压力曲线法所得到的相对渗透率曲线结果进行对比。表2为所有20块岩芯采用JBN方法和本文所述新方法计算得到的相对渗透率曲线各特征点值与毛管压力曲线法所得到的特征点值的平均偏差对比。

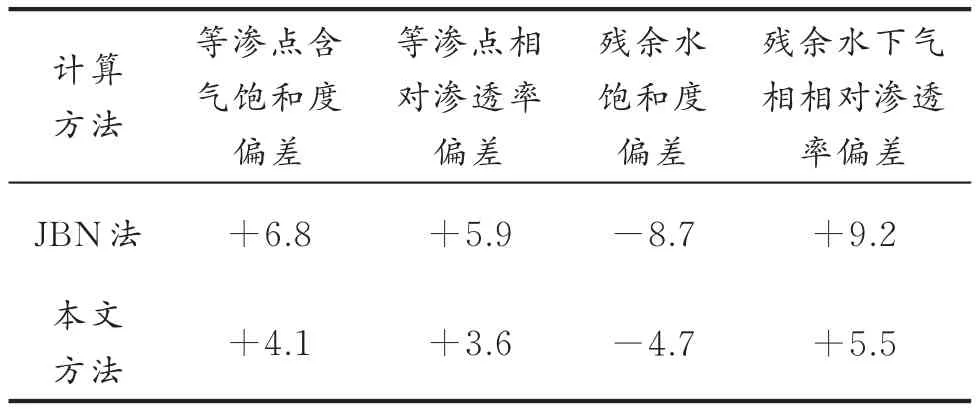
表2 不同方法计算结果偏差对比Table 2 Er ror bar of differ ent calculation methods%

从表2中可以看出，和常规JBN方法相比，采用本文中新方法得到的相对渗透率曲线各特征值都更接近于毛管压力曲线法得到的相渗曲线的特征值，说明了本文方法得到的相渗曲线较JBN方法得到的曲线更为准确，验证了本文方法的可靠性。

从表2中还可以看出，两种不同的计算方法相比，采用常规JBN方法得到的等渗点含气饱和度和相对渗透率较本文方法结果偏大，残余水饱和度偏小且残余水条件下的气相相对渗透率偏大，这是因为常规的JBN方法没有考虑到致密岩芯的动态启动压力梯度效应和应力敏感效应，导致计算中所得到的岩芯渗流能力较实际情况偏乐观，因此在相对渗透率曲线上表现为等渗点相对渗透率高，束缚水饱和度低等一系列特征。

在致密储层的实际开发过程中，储层的流体压力是一个不断下降的过程，根据动态启动压力梯度理论和应力敏感理论，储层的启动压力梯度会随之升高[12]，渗透率会随之下降[18⁃20]。因此，在气藏的不同开发阶段，采用本文新方法和JBN方法得到的相渗曲线会有不同的差异。以表1中的岩心2为例，分别在同一上覆地层压力（62 MPa），不同孔隙流体压力（26、20、15、10 MPa）下开展相对渗透率实验测试，并采用两种方法分别绘制了各个阶段的相对渗透率曲线，如图2所示。从图2可以看出，在新方法中，考虑动态启动压力梯度和应力敏感性的情况下，采用本文方法计算得到的相渗曲线和JBN方法得到的曲线均呈现出类似前文中所描述的差异：水相相对渗透率降低速度加快，气相相对渗透率上升速度减缓，等渗点相对渗透率不断下降，残余水饱和度不断升高。这是因为随着孔隙压力的下降，岩芯启动压力梯度逐渐上升，同时有效渗透率逐渐下降，这两种因素对于渗流的影响随着孔隙压力的下降越来越显著，造成流体在岩芯中的渗流难度不断增大，因此考虑这两种因素在内的新方法得到的相对渗透率曲线和传统的JBN方法得到的曲线的差异就越来越大，具体表现为：随着开发过程中孔隙流压的不断下降，和JBN方法相比，新方法计算得到相对渗透率等渗点持续左移，等渗点相对渗透率下降，束缚水饱和度不断上升，束缚水条件下的气相相对渗透率持续下降，且孔隙流压越低，两种方法得到的曲线差异越大。

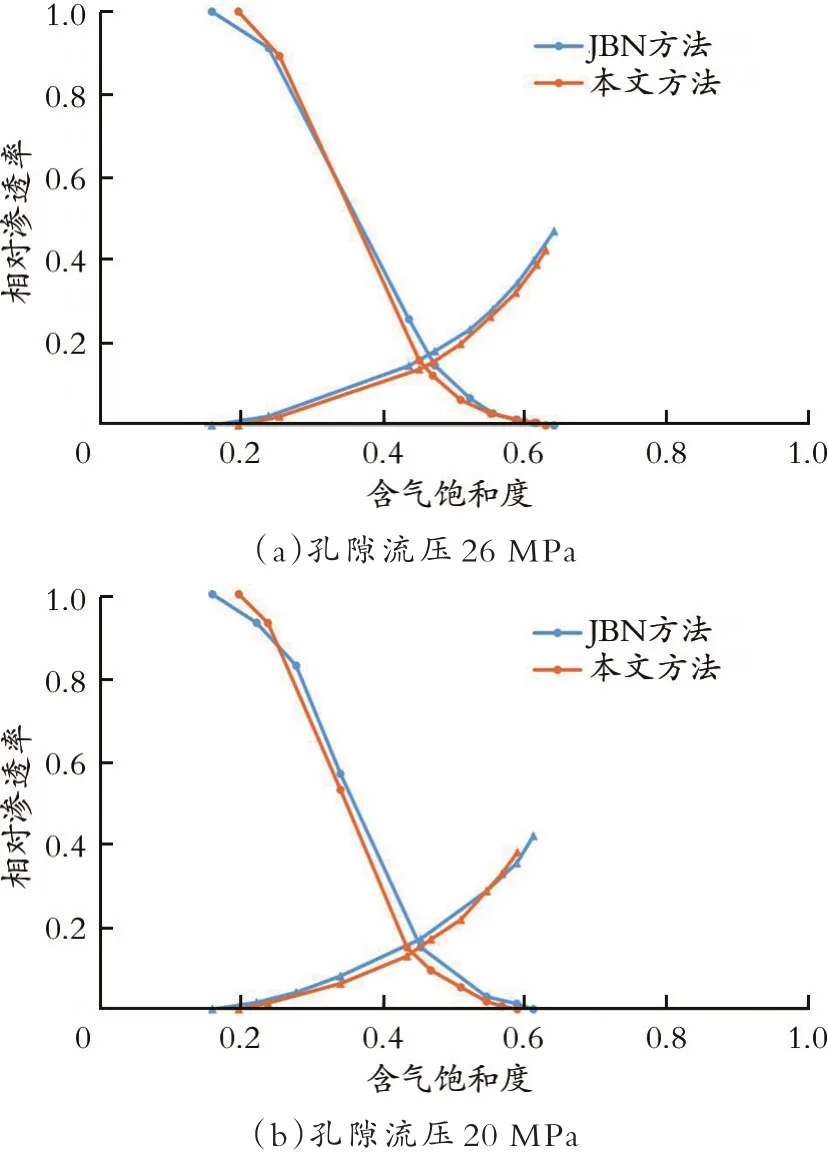
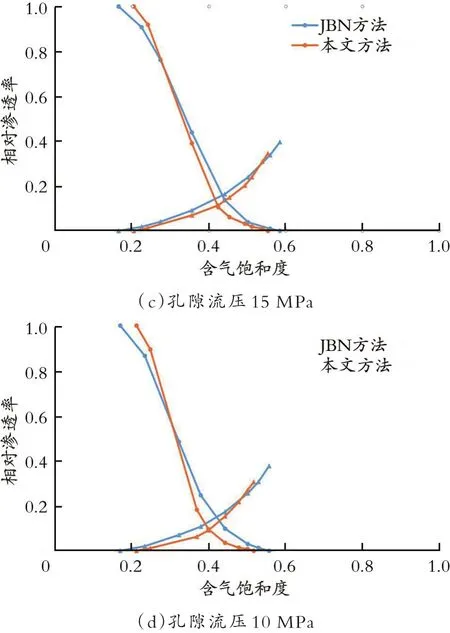
图2 不同流压下实验岩芯2的相对渗透率曲线Fig.2 The relative permeability curve of core 2 under different flow pressure

在致密气藏实际开发过程中，上覆地层压力基本保持不变，而储层孔隙流体压力则会随着孔隙中流体的采出而不断下降，造成储层启动压力梯度的不断上升和渗透率的不断下降。如果采取常规的JBN方法进行相对渗流曲线的计算，势必造成计算的误差，且开发阶段越靠后，误差越大。

4 结 论

（1）在分析致密气藏特殊渗流机理的基础上，建立了考虑动态启动压力梯度和应力敏感效应的致密气藏两相渗流计算方法。

（2）在考虑动态启动压力梯度和应力敏感性的情况下，气、水两相的渗流能力均有明显下降，两相共渗区域范围变窄，其中水相相对渗透率降低速度加快，而气相相对渗透率上升速度有所减缓，等渗点相对渗透率降低，实验结束时，岩芯的残余水饱和度升高，残余水饱和度下的气相相对渗透率有所降低。

（3）不同孔隙压力下的相对渗透率实验结果表明，随着孔隙流体压力的下降，动态启动压力梯度和应力敏感性对于渗流的影响越来越显著，因此考虑这两种因素在内的新方法得到的相对渗透率曲线和传统的JBN方法得到的曲线差异越来越明显。

（4）在致密气藏实际开发过程中，储层孔隙流体压力不断下降。如果采取常规的JBN方法进行相对渗流曲线的计算，势必造成计算的误差，且开发阶段越靠后，误差越大。因此，必须将储层的动态启动压力梯度和应力敏感效应考虑在内，进行相应的相对渗透率曲线计算。