深度学习椭圆第一定义

田淑玲

(黑龙江省哈尔滨市哈尔滨师范大学 150025)

椭圆定义的掌握与应用，应抓住椭圆的定义内涵：距离之和等于常数，且大于两定点之间的距离.

一、直接型

题干中直接标明长轴、短轴、顶点、焦距、通径、离心率等内容，可直接利用公式求出a、b、c进而求出椭圆方程；或给出形式比较直观,可直接观察出所给表达式符合椭圆定义等均可直接写出椭圆方程.

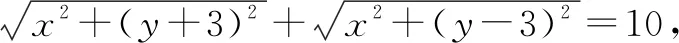
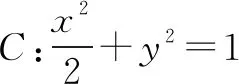
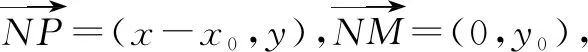
二、间接型

题干中所给信息不够明显，但往往会给比较明显的信号词，如:线段垂直平分线(线段垂直平分线上任意一点，到线段两端点的距离相等)、平行线(同位角、内错角相等)、等腰或等边三角形(等角对等边)等，进行转化，得出PF1+PF2=2a>F1F2=2c的形式，进而求出椭圆方程.

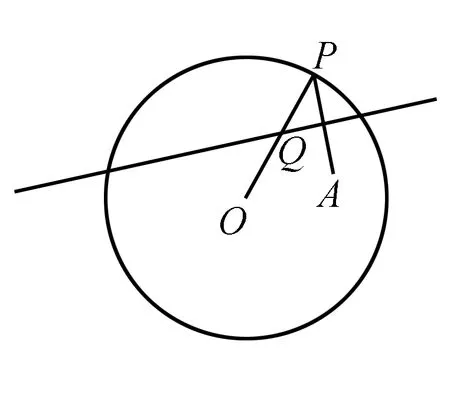
图1

例3如图1，圆O的半径为定长r，A是圆O内的一个定点，P是圆O上的任意一点，线段AP的垂直平分线l和半径OP相交于点Q，当P在圆上运动时，点Q的轨迹是什么？为什么？

解析根据题干中信息，l是AP的垂直平分线，由线段垂直平分线的性质可知，需连接AQ，则|AQ|=|PQ|，故|AQ|+|OQ|=|PQ|+|OQ|=r,点A在圆内，r大于|OA|，所以Q点轨迹为椭圆.

思考：当点A在圆O外部时，Q点轨迹为什么？为什么？

例4已知动圆M，它和圆C1:(x+1)2+y2=36相内切，且和圆C2:(x-1)2+y2=4相外切，求动圆M圆心的轨迹方程.

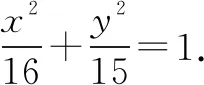
例5 已知圆的方程来：x2+y2=4，若抛物线经过A(-1，0)，B(1，0)，并且以圆的切线为准线，则抛物线焦点的轨迹为什么？方程是什么？

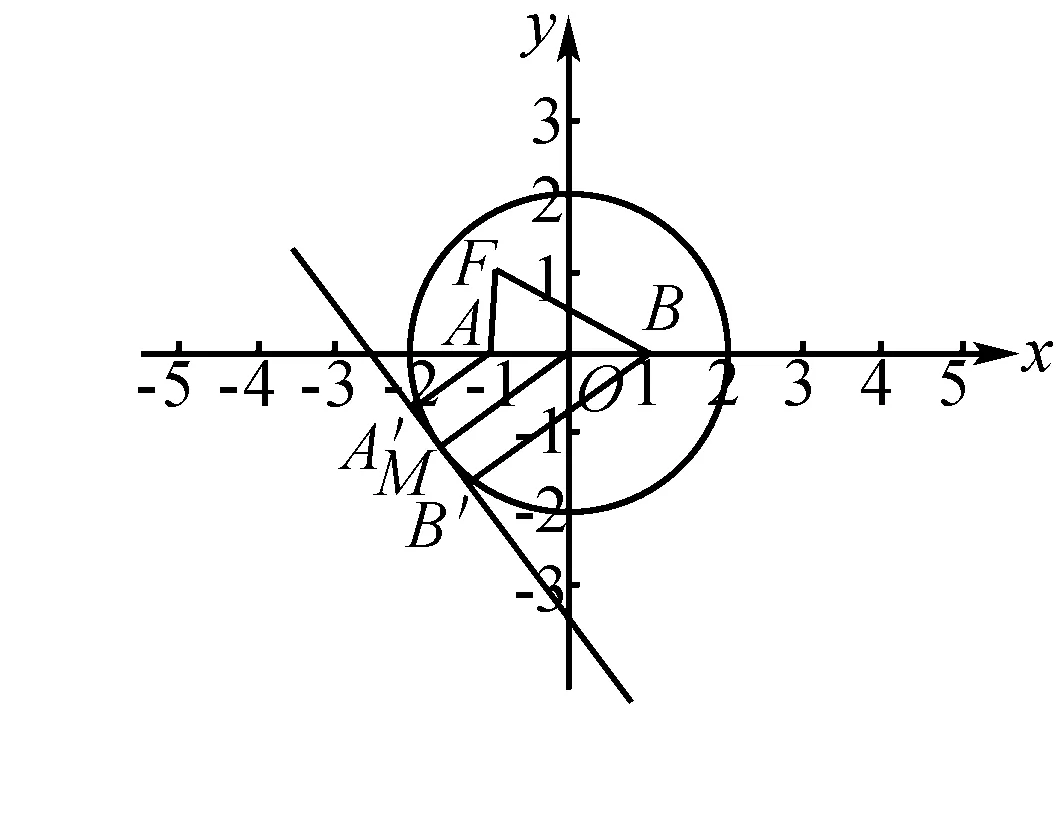
图2

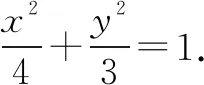
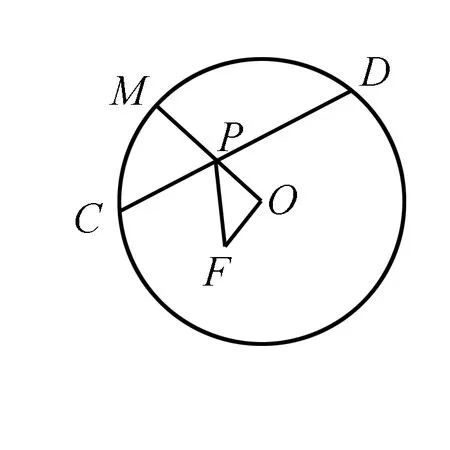
图3

例6 (2017年枣庄模拟)如图3所示，一圆形纸片的圆心为O，F为圆内的一点，M为圆周上一动点，将纸片折叠，使得点M与点F重合，然后抹平纸片，折痕为CD，若设CD与OM交于P，与则P点的轨迹是什么？

解析考虑到M与点F重合，连接MF，交CD于点Q，则△MQP≌△FQP,|PM|=|PF|,|PF|+|PO|=|OM|>|OF|,故点P的轨迹为椭圆.

例7 (2016全国1卷节选)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1，0)(与x轴不重合)，l交圆A于C、D两点，过点B作AC的平行线，交AD于点E，证明|EA|+|EB|为定值，并写出点E的轨迹方程.

通过以上习题，不难发现，在求椭圆方程时，我们可按照以下步骤来进行求解(1)做判断，根据题中条件判断所求轨迹或方程是否为椭圆；(2)设方程，焦点不确定时要注意分类讨论；(3)找关系，根据已知条件，建立a、b、c的关系；(4)求解，得到方程.