探析2019年全国Ⅰ卷文科第20题
张兵源
(福建省漳州市教育科学研究院 363000)
一、试题呈示
题目已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导函数.(1)证明:f′(x)在区间(0,π)存在唯一的零点;(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
试题分析2019年高考新课标Ⅰ卷文科第20题,以三角函数为载体考查导数的应用.试题平和——表述简明,言简意赅;稳定——平稳过渡,风采依旧.试题分为两步,具有梯度性,层次感强,既能够让不同的考生都有所收获,也能够让优秀的学生脱颖而出.第一小题证明导函数存在唯一的零点,需要借助导数工具结合零点存在性定理求证;第二小题已知恒成立问题求参数的取值范围,融函数,导数,不等式等众多知识点于一体,深刻体现了对学生能力考查,对中学数学教学有良好的导向作用.实际解题时,对考生运用所学知识寻找合理的解题策略和考生的逻辑思维,运算求解能力都提出很高的要求,能有效地反映考生的思维层次的高低,给优秀学生提供充分施展才能的空间.
二、试题解析
1.对第一小题的解析
思路1直接法
f′(x)=cosx+xsinx-1,记g(x)=f′(x),转化为证明g(x)在(0,π)存在唯一的零点.
g′(x)=xcosx,

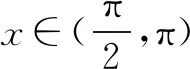

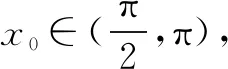
所以f′(x)在(0,π)存在唯一的零点,得证.
点评思路1对f(x)求导,得到导函数f′(x),将f′(x)看成一个新的函数g(x),对g(x)再求导,借助导数考察g(x)的单调性,结合零点存在性定理证明出g(x)在(0,π)存在唯一的零点.思路清晰自然,直奔目标,迅速求解.
思路2间接法
令f′(x)=0,得cosx+xsinx-1=0,即cosx+xsinx=1.
记φ(x)=cosx+xsinx,转化为证明直线y=1与曲线φ(x)=cosx+xsinx在(0,π)有唯一一个交点.
φ′(x)=xcosx,

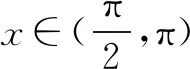
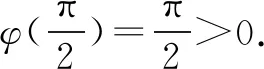
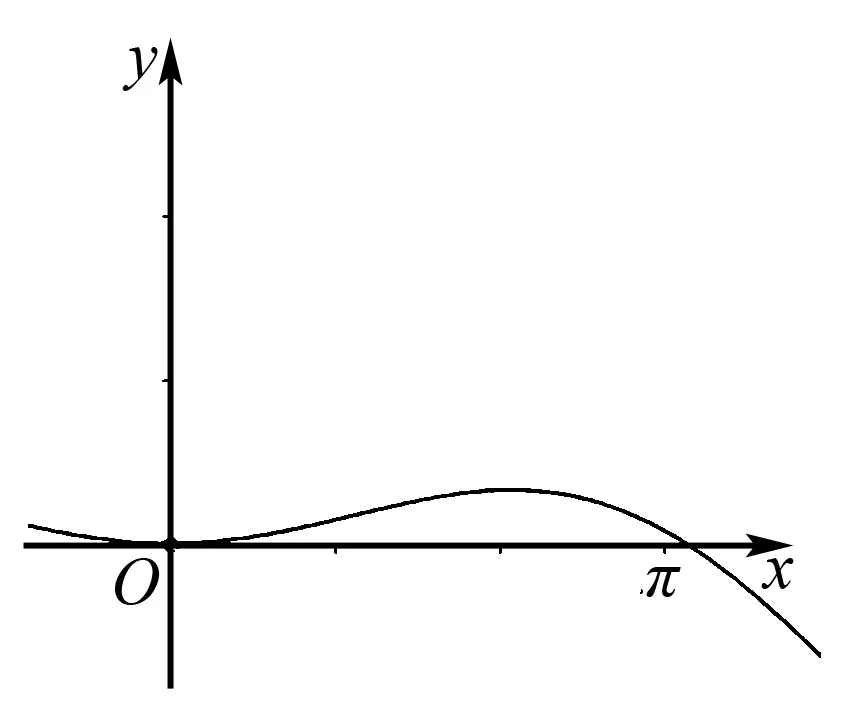
又φ(0)=1,φ(π)=-1<0,画出曲线φ(x),如图1所示.
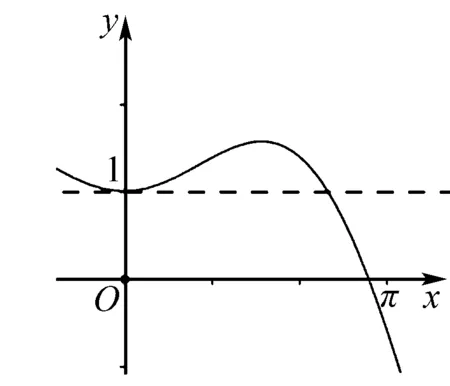
图1
故直线y=1与曲线φ(x)=cosx+xsinx在(0,π)只有一个交点,得证.
点评思路2借助函数与方程思想,将问题转化为证明直线与曲线有一个交点,是数形结合思想的深刻体现.
2.对第二小题的解析
思路1由f(x)≥ax,得2sinx-xcosx-x-ax≥0.
记g(x)=2sinx-xcosx-x-ax,则g(x)≥0.显然g(0)=0,g(π)=-aπ.
g′(x)=cosx+xsinx-a-1,g″(x)=xcosx.

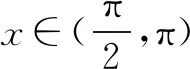
g′(0)=-a,g′(π)=-2-a.
若-a<0,即a>0时,必存在δ>0,当x∈(0,δ)时,g′(x)<0,g(x)在x∈(0,δ)单调递减,g(x) 若-a≥0,即a≤0时, 当-2-a≥0,即a≤-2时,g′(x)≥0,g(x)在x∈(0,π)单调递增,g(x)≥g(0)=0,符合题意. 当x∈(0,x0)时,g′(x)>0,g(x)在x∈(0,x0)单调递增; 当x∈(x0,π)时,g′(x)<0,g(x)在x∈(x0,π)单调递减. 又g(0)=0,g(π)=-aπ≥0. 所以g(x)≥0,符合题意.综上有a≤0. 点评思路1是构造出一个新的函数g(x),求导,对参数a进行分类讨论.难点在于如何找到讨论的点.由于g′(0)=-a,g′(π)=-2-a,所以不难想到必须对这两个端点值与零进行分类讨论. 思路2由f(x)≥ax,得2sinx-xcosx-x-ax≥0. 记g(x)=2sinx-xcosx-x-ax,则g(x)≥0.显然g(0)=0. g′(x)=cosx+xsinx-a-1,令g′(0)≥0,得a≤0. 下证当a≤0时有g(x)≥0. 当a≤0时,g′(x)=cosx+xsinx-a-1,g″(x)=xcosx. g′(0)=-a≥0,g′(π)=-2-a. 当-2-a≥0,即a≤-2时,g′(x)≥0,g(x)在x∈(0,π)单调递增,g(x)≥g(0)=0,符合题意. 当x∈(0,x0)时,g′(x)>0,g(x)在x∈(0,x0)单调递增; 当x∈(x0,π)时,g′(x)<0,g(x)在x∈(x0,π)单调递减. 又g(0)=0,g(π)=-aπ>0. 所以g(x)≥0,符合题意. 综上有a≤0. 点评思路2先求出符合题意的必要条件再验证充分性.由于g(x)在端点处的函数值刚好是零,且g(x)≥0恒成立,因此必有g′(0)≥0,从而解出a≤0.但是还必须证明a≤0就是使得g(x)≥0恒成立的参数a的取值范围. 思路3当x=0时,有0≥a·0,a∈R. 记T(x)=2xcosx-2sinx+x2sinx,T′(x)=x2cosx. T(0)=0,T(π)=-2π<0. 当x∈(0,x0)时,T(x)>0,φ′(x)>0,φ(x)在x∈(0,x0)单调递增; 当x∈(x0,π)时,T(x)<0,φ′(x)<0,φ(x)在x∈(x0,π)单调递减. 又φ(π)=0,画出φ(x)的图象,如图2所示. 图2 所以φ(x)的最小值为0,故a≤0. 综上有a≤0. 点评思路3是分离变量转化为求函数的最值.将参数a与变量x分离,转化成a≤φ(x)min.由于φ(x)的最值在端点处往往取不到,所以需要借助极限的知识或者洛必达法则求解. 思路4由第一小题知f′(x)在(0,π)存在唯一的零点,设为x0.且当x∈(0,x0)时,f′(x)>0,f(x)在(0,x0)单调递增;当x∈(x0,π)时,f′(x)<0,f(x)在(x0,π)单调递减.又f(0)=f(π)=0,即当x∈[0,π]时,f(x)≥0.又有∀x∈[0,π]时,f(x)≥ax.所以a≤0.综上有a≤0. 思路5由题意有f(π)≥aπ,又f(π)=0,所以aπ≤0,即a≤0.由第一小题知f′(x)在(0,π)存在唯一的零点,设为x0.且当x∈(0,x0)时,f′(x)>0,f(x)在(0,x0)单调递增;当x∈(x0,π)时,f′(x)<0,f(x)在(x0,π)单调递减.又f(0)=f(π)=0,即当x∈[0,π]时,f(x)≥0.又当a≤0,x∈[0,π]时,ax≤0.所以f(x)≥ax.综上有a≤0. 变式1已知函数f(x)=ex,g(x)=x2+ax-2xsinx+1. 解析(1)略.(2)由已知有ex-x2-ax+2xsinx-1≥0. 设h(x)=ex-x2-ax+2xsinx-1,则h(x)≥0.显然h(0)=0. h′(x)=ex-a-2x+2sinx+2xcosx.令h′(0)≥0得a≤1. 下证当a≤1时有h(x)≥0. 当a≤1时,h′(x)=ex-a-2x+2sinx+2xcosx.显然ex-a≥0. 记T(x)=-2x+2sinx+2xcosx.由0 故h′(x)>0.所以h(x)在x∈[0,1)单调递增,h(x)≥h(0)=0. 综上,a≤1. (1)求函数f(x)和g(x)的解析式; 解析(1)f(x)=cos2x,g(x)=sin2x.(过程略) 则h′(x)=cosx+cosxcos2x+2sin2x(2-sinx). 因此,存在唯一的x0符合题意. 全国卷导数压轴试题不管文科还是理科,试题都能够延续往年全国卷试题中导数压轴题的形式与命题风格,表述简洁,内涵丰富,以学生熟悉的一次函数,二次函数,三角函数及对数型函数,指数函数的组合为载体,以函数的单调性为背景,将函数,方程与不等式等融汇联系在一起,考查函数极值的概念,导数的运算法则,考查考生运用导数工具灵活分析问题与解决问题的能力. 本道文科高考试题所涉及到的知识点与求解方法体现了高考不回避热点问题,不回避学生平时常考的考点,常用的方法.这就启发我们在高三复习时一定要讲透题型及其相应的求解策略.比如对于本题的第二小题是常见的恒成立问题求参数的取值范围,如果教师在平时的复习时能够把此类题型的求解方法讲解清楚,学生就能够内化成自己的能力,从而精准提分. 除此以外,教师要加强对数学问题的探究性教学,重视变式训练,注重对同一个习题多个知识点的改编,重组和变式,训练和优化学生的思维品质.要树立备考以提升学生数学学科核心素养为出发点,全方位地培养学生的综合处理数学问题的能力,让学生在教学活动中体验数学活动经验,掌握数学本质,感受数学思想,学会数学地思考问题,用数学的眼光观察,分析和解决问题.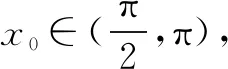

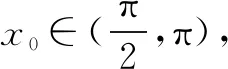
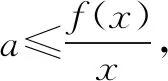
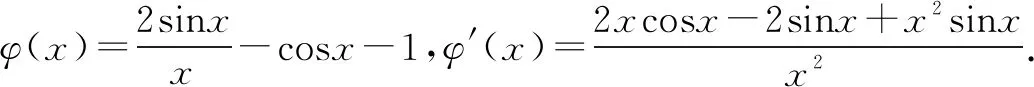

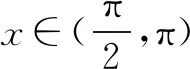
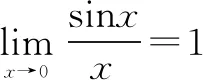
三、试题变式
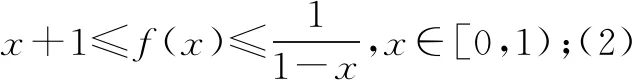
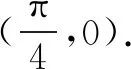
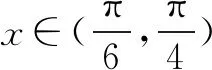

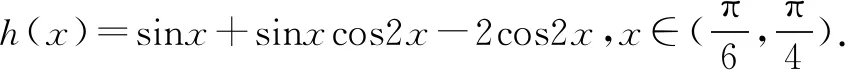

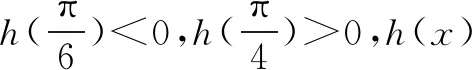
四、教学启示

