基于2019全国卷一道圆锥曲线问题的课堂探究

张海宾

(安徽省合肥市一六八中学 230601)

学生作为课堂的主体，在学习过程中的参与状态和参与度是影响教学效果的重要因素，在具体课堂教学中应鼓励学生积极参与教学活动，包括思维的参与和行动的参与，使学生始终处于主动探索问题的积极状态，从而培养思维能力.下面就以2019年全国Ⅰ卷理科选择题第10题课堂教学为例.

例已知椭圆C的焦点为F1(-1，0)，F2(1，0)，过F2的直线与C交于A,B两点，若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为( )

分析本题主要检验学生能否对圆锥曲线相关知识做到灵活运用，考查考生的化归与转化能力，运算求解能力，注重对数学运算、逻辑推理等数学核心素养的考查.

在选择、填空题中，尽量避免用代数方法解决圆锥曲线问题，不仅费时、费力，而且影响考生的考试情绪，应该试着寻找图形中的几何关系，有时能起到事半功倍的作用.所以在平时的教学中教师应该引导学生多思考，多质疑，多途径解决圆锥曲线问题.对于此题的讲解我首先和学生们一起给出了我的解答过程.

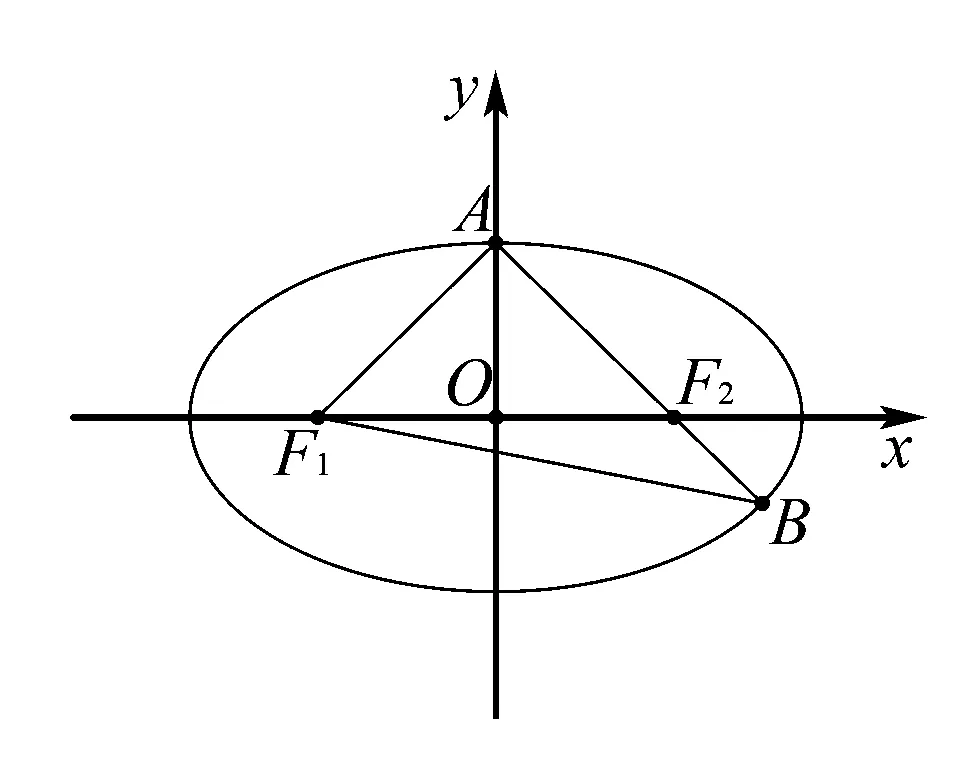
得到答案并不是解题教学的目的，对于很多同学可能只是机械地接受，并没有主动地思考.所以此时我告诉学生对于这题我是观察图形中△AF1F2和△AF1B两个三角形有一公共角，利用他们的余弦值相等建立方程来解决问题的.那么还有没有其他的解题思路呢？欢迎同学们说出你们的想法？我给予学生们两分钟的思考时间后有学生甲举起了手，我立即请他讲述他的思路.

对于学生甲的解法我给予了极大的肯定和表扬，只为激起其他同学思考和回答的热情，此时学生乙自告奋勇地说自己还有有其他解法.

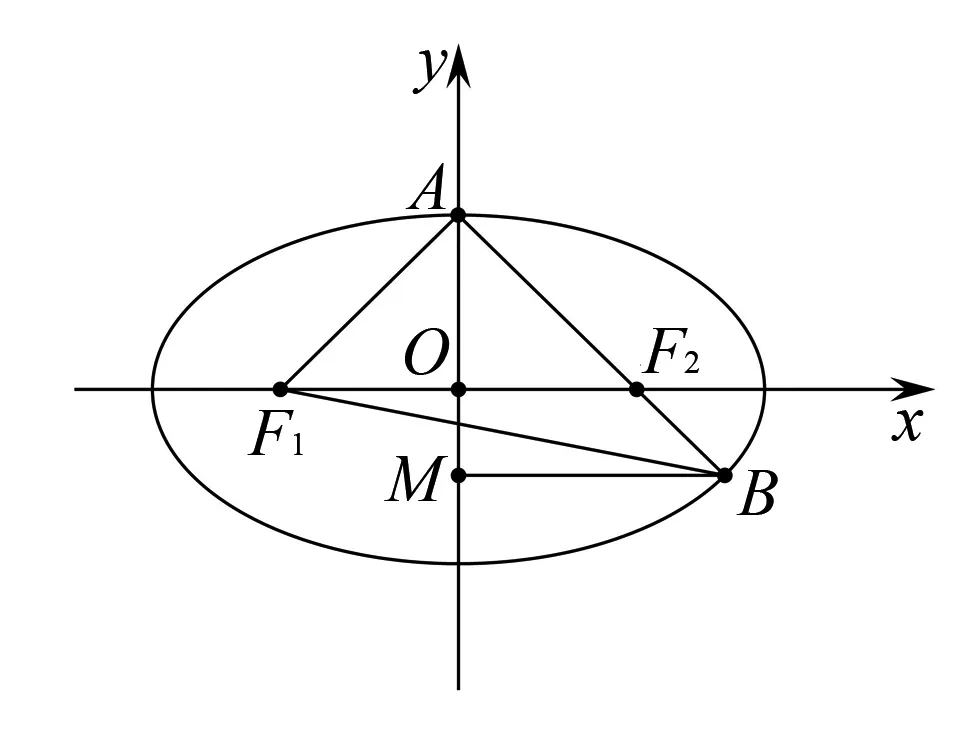
到此为止，课堂气氛达到了一个小的高潮，唤起了同学们极大的热情，不断有学生争先恐后地举手，其中有位同学说也可以由B作BN⊥x轴于N点，利用△AOF2～△BNF2来求得B点坐标，还没等该同学说完，班级同学不约而同地说，这方法和前面的方法是一致的啊.这个时候作为老师我给予了这位同学我的表扬：上课认真听课，认真思考，活学活用.也对其余同学说既然你们觉得方法相同，那你们还有什么不一样的方法吗?

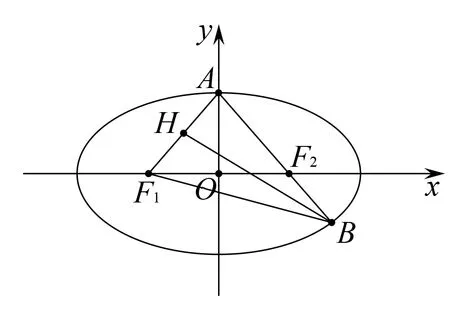
学生丙站了起来，说可以用面积相等，同学们都安静了下来，我们一起来看听学生丙的方法.

一千个眼中就有一千个哈姆雷特，每一位学生都是宝藏，只要我们愿意去挖掘，总会有意想不到的收获.