基于加权马氏距离法的砂土液化评级模型

张少腾 ,余 娟 ,刘 晶 ,高明智 ,李 佩 ,刘 飞

（1.徐州市数字地震台网中心,江苏 徐州 221000;2.徐州市地震台,江苏 徐州 221000;3.河南省地质矿产勘查开发局第四地质勘查院,郑州 450000;4.江苏省地质矿产局第五地质大队,江苏 徐州 221000）

0 引言

进行砂土液化判别可以有效地预测砂土液化危险区域,以此制定有针对性的预防措施,对生命和财产安全具有重要意义[1]。

目前,关于砂土液化判别的研究可分为单一指标法和综合指标法[2]。其中,综合指标法是选用液化相关的各种指标,建立数学模型判别样本所属。前人运用模糊数学法[3]、人工神经网络法[4-6]、灰色理论法[7]等方法对砂土液化预测进行了尝试,但出现了收敛数度慢[8]、盲目性大[9]等缺陷。颜可珍等运用距离判别法[2]的运用取得了良好的效果,但是未充分考虑权重对砂土液化预测结果的影响。并且,前人的研究仅对砂土状态笼统划分为液化与不液化,这给有针对地治理砂土液化提供难度;再者,以往综合分析法的砂土预判,多采用地震发生后现场实测样本,建立的判别模型仅基于有限几十组数据,这对于综合指标这种统计学方法来讲,样本数过少,容易造成因个别样本的局部偏差影响最终判别式。

本文拟采用层次分析法与模糊评判法对砂土液化指标进行加权,结合马氏距离判别分析法,建立加权马氏距离判别分析模型;利用《建筑抗震设计规范》中液化等级划分标准将砂土液化状态分为轻微液化、中等液化以及严重液化三个级别,选用粒径、标准贯入击数、层厚三项指标来判别砂土液化。最终结果与工程实测等级、马氏距离判别法和灰色综合评判法对比,结果显示预测等级与实测等级具有较好的一致性,与参与比较的两种判别法相比具有较低的误判率。

1 加权马氏距离判别模型的建立

1.1 砂土液化的影响因子

砂土液化判别指标的选择是判别砂土液化的前提,判别指标的选择直接关系到预测结果的准确与否,选择判别指标既要考虑到指标选择的惯用原则,也要考虑到拥有信息的现实因素。砂土液化机理特性复杂,受各种因素影响。根据砂土液化机理,影响地震砂土液化的因素共可分为三大类（图1）。第一类物理要素,主要指砂土中影响其自身液化的各种物理特性,包括砂土粒径、密度、粘接强度等。第二类环境要素,主要表现为周围环境对砂土本身造成的状态以及力学性能的改变,包括上覆土层厚度、地下水位高度、排水渗水能力等。第三类地震要素,主要指地震的基本情况,包括震级、震中距以及持续时间;在地震研究中也常有用地震加速度峰值、地震烈度来表征地震的强度以及危害性。

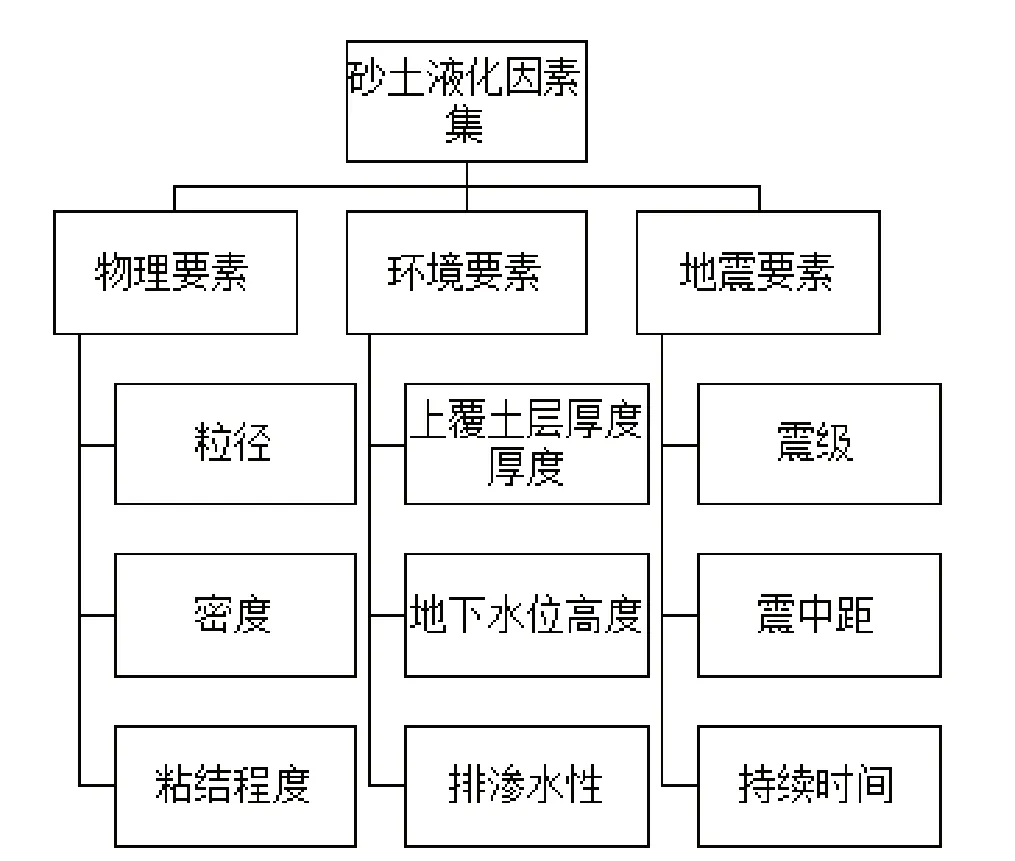
图1 砂土液化因素集Fig.1 Factor sets of sand soil liquefaction

前人研究表明[10-11]砂土粒径越大、质地越密,砂土的抗液化能力越强。在工程取样过程中,扰动样不能真实反映样品密实度,只能采取标准贯入击数代替。标准贯入击数越大,抗液化能力越强。赵艳林,杨绿峰等[12]证明上覆应力主要受地下水位以及土层埋深影响,土层埋深越大,水位越深,有效上覆应力也越大。而上覆应力与造成砂土液化的水平地震剪应力成正相关性。地震时,在土层中引起的等效均匀循环剪应力随地震加速度峰值的增大而增大。按照《建筑抗震设计规范》,砂土液化抗液化强度与层厚度成反比。

根据研究和已有资料综合考虑,粒径、标准贯入击数,土层厚度,地震加速度峰值,土层埋深以及地下水位深度六个指标可作为影响砂土液化的主要因素。但随着因素的增加,各指标的权重分配更为复杂,不能真实反映指标对液化结果的最终影响,故而将影响液化的六项指标中的土层埋、地下水位以及地震峰值加速度等三项指标定量。从工程样本数据中选取砂土液化的评价深度为20 m,地下水位埋深为1.5 m的样本进行计算,选取地震峰值加速度为0.10 g,将粒径、标准贯入击数以及土层厚度作为变量进行研究。

1.2 评价因子权重确定

权重是根据主观评价和指标的自身固有特性两个方面因素综合决定,其权值分别利用主观赋权法和客观赋权法来确定[10]。主观赋权与客观赋权相结合,可以根据所掌握资料以及拥有专家的数量建立更为可靠的权值矩阵。

层次分析法（Analytic Hierarchy Process,AHP）是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难以完全定量分析以及参考因素较多的问题。当比较n个因子X=(x1,x2,…,xn)对某因素Z的影响时,可以采取对因子两两比较建立成对比较矩阵的办法。采用上述方法,通过专家打分获得最终结果如表1。

客观权重赋值是由单因素的模糊评判获得对应率之后,再经归一化后求得。设参加评判的样本共有n个,分别利用标贯击数,粒径,层厚这3个指标进行单因素评判获得的结果与实际相符的样本个数n1,n2,n3,则单因素评判的对应率为：

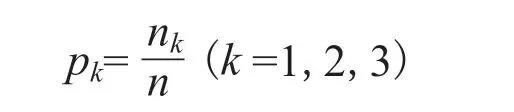
对结果进行归一化处理,得

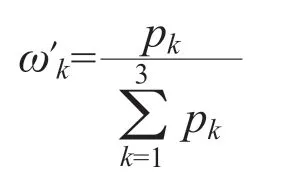
本文共搜集评判样本120例,对样本集进行单因素模糊评价,得到粒径、标贯以及土层厚度的客观权值分别为0.305,0.357,0.338。

利用下述公式得出第k个指标的权重为：

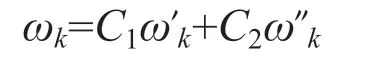
其中,C1+C2=1

式中,C1,C2为权量分配系数,可由实际情况确定。ω’k为模糊评判的第k个指标的权值,ω’k为利用层次分析法专家打分获得的第k个指标的权值。本文选取C1,C2均为0.5,最终得各因素权重值见表2。

表1 砂土液化因子主观权重Table 1 Subjective weight of sand soil liquefaction factors

表2 砂土液化影响因子综合权重Table 2 Comprehensive weight of sand soil liquefaction factors

1.3 加权马氏距离判别模型建立

马氏距离判别法[13]记样本资料矩阵为：

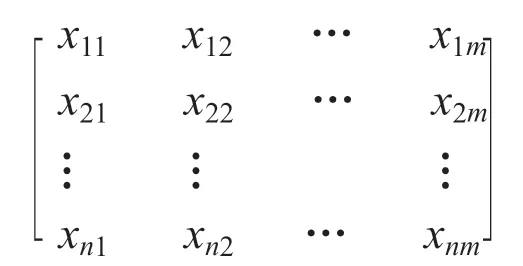
其中：xnm代表第n个样本的第 m个指标值;Xi=(xi1+xi2+…+xm)表示第i个样本的m个指标观测值;设总体D1、D2以及D3的均值向量μ1≠μ2≠μ3,协方差Σ1≠Σ2≠Σ3,则样本X到各总体的马氏距离分别为：

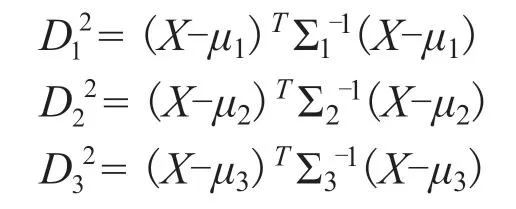
判别规则为：

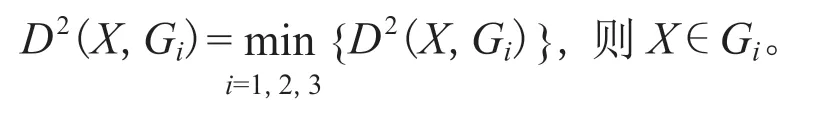
为避免夸大某一指标的作用,在马氏距离的基础上加入指标的权重,以区分各指标的重要性,将综合权重值赋于马氏距离公式,因此加权马氏距离的平方可表示为：

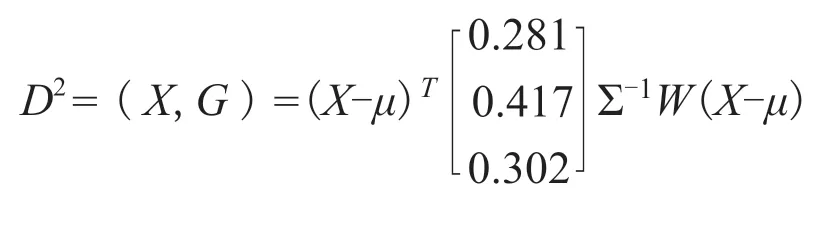
2 模型的检验

2.1 数据归一化

根据前面所述加权马氏距离分析的基本思想,本文选择了某地120个工程案例中有明确结论的实例作为研究对象（本文列出30组样本数据）,按照《建筑抗震设计规范》（GB50011-2010）的相关规定对各孔进行了砂土液化判别。

粒径、标贯击数以及土层厚度的单位和量纲均不统一,不便归类计算,因此先其进行标准化处理,可利用下列公式进行处理：

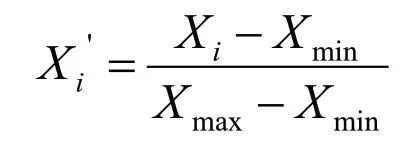
2.2 模型检验

对120个样本进行主成分分析,求出权矩阵W,利用DPS软件[14]计算,得到相关系数矩阵,并由该矩阵求出其非零特征根。

在砂土液化预判研究中,将液化等级详细区分有助于对不同液化区域进行区别处理。将液化等级分轻微液化、中等液化以及液化严重三个等级,同时,将样本分为参考样本和待评价样本两组。

对判定为液化的土层,按《建筑抗震设计规范》中砂土液化判别公式及液化等级划分标准（表3）,计算每个钻孔的液化指数,并划分场地的液化等级。液化等级划分标准见表3。砂土液化判别公式如下：

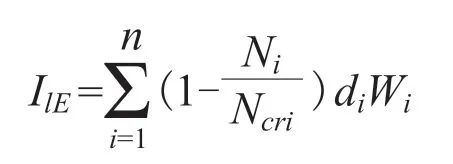
式中：IlE为液化指数;n为钻孔个数;Ncri、Ni分别为i点标贯击数的临界值和实测值,当临界值小于实测值时应取临界值;di表示土层厚度（m）;Wi表示土层厚度的层位影响权函数值。

表3 砂土液化等级划分表Fig.3 Grade division of sand soil liquefaction

依据上述公式及等级划分表求得实测液化等级见表4,同时,根据表中所列指标数据以及加权马氏距离判别分析原则即可以确定待评砂土液化评级情况。本文同时采用马氏距离判别法以及灰色综合评价法对所有样本进行砂土液化判别。

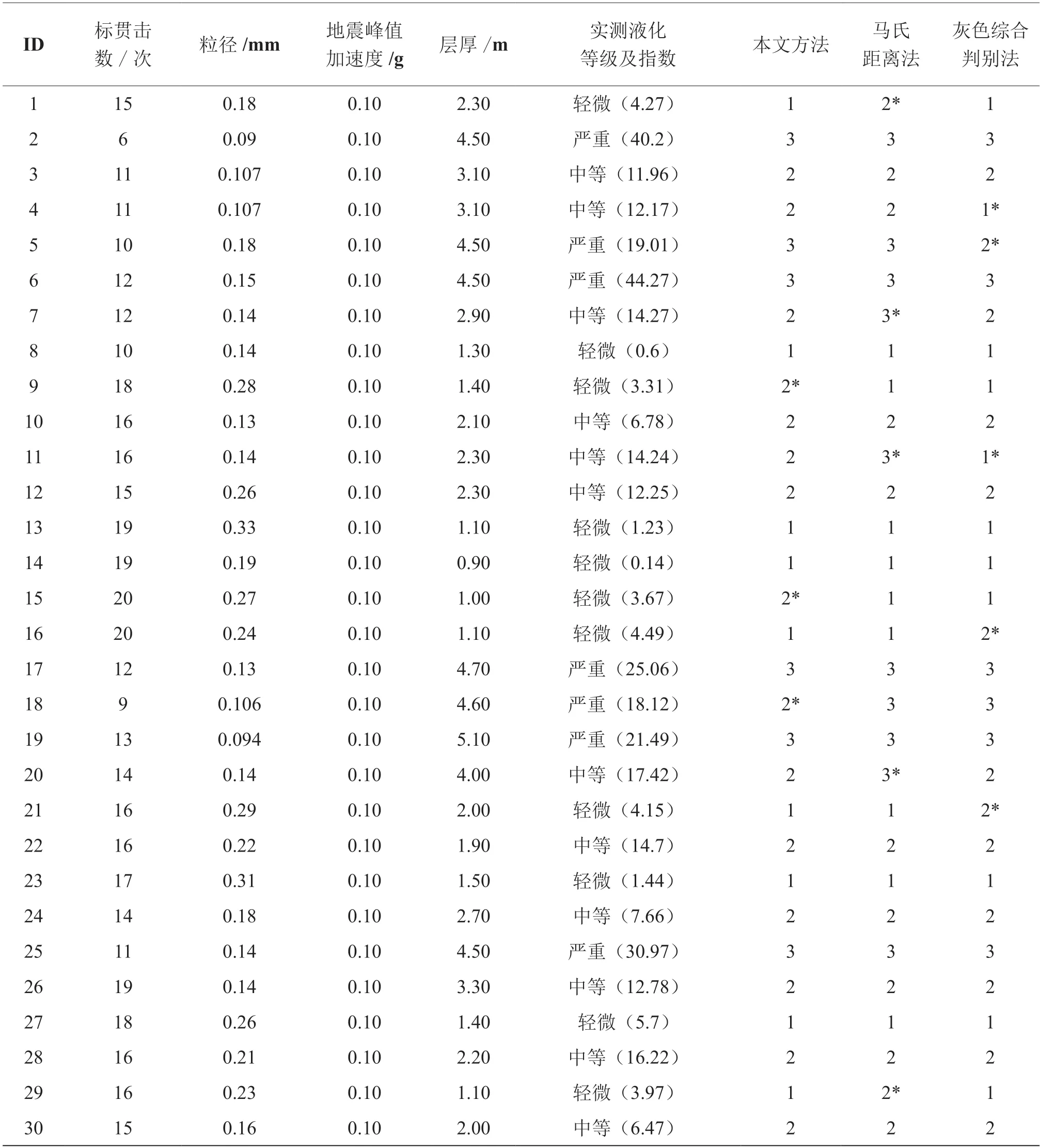
表4 不同方法判别结果对比Table 4 Comparison of discrimination results of different methods

对计算出的样本模型进行逆运算和待评价样本检验,从表中可以看出,待评价样本在使用本方法最终检验结果与实测样本结果吻合,9、15、18号样本在逆运算时出现误差。

使用马氏距离判别法样品1、7、11、20、29均出现误判,结合所有工程样本误判率为27﹪,使用灰色综合判别法样品4、5、11、16、21出现误判,总体误判率为23﹪,而加权马氏距离判别法只有9、15、18号样品在回判学习中发生了误判,总体误判率为12%。这说明加权马氏距离判别法相对于马氏距离法、灰色综合评判法具有更高的预报效能。因此,该方法能够有效预测砂土液化并提高预测精度,有利于对具有危险性的地基基础进行针对性处理。

3 讨论

(1)加权马氏距离判别法与实测工程样本结果基本一致,证明其具有一定可行性。在与前人使用的马氏距离判别法和灰色综合评判法的结果对比中,具有更高准确性。同时,它是基于经验的基础上进行计算,随着运用案例以及区域的增加,可对权重及指标进行完善和调整,加强其地域适用性。

(2)模型中选取的数据均采用工程液化判定实例,相对于前人常采用的地震液化实例样本更多,尽可能避免小样本造成的统计误差影响,使研究数据更可靠,更有实际工程应用价值。

(3)将砂土状态分为三个等级,轻微液化、中等液化以及严重液化,采用等级式液化评价,避免了前人液化评价中只有液化和非液化两种状态的片面性缺陷,可依据不同等级采取对应措施对基础进行加固和预防。

(4)本文为展示方法的可行性,又因为样本数据的限制,仅采用三个指标进行砂土液化评判,具有一定的局限性,在选取更多指标的情况,指标、权重的选择需进一步研究。