不同采购策略下渠道成员定价及订货决策研究

杨天剑 田建改 Ruhai Wu

1 (北京邮电大学经济管理学院, 北京 100876)

2 (DeGroote School of Business, McMaster University, Canada L8S 1A1)

引 言

2010 年以来网络团购风靡中国， 一定数量的用户借助网络渠道组团， 从而以低价购买到同一种商品或服务， 其实质是网络商店实施了数量折扣策略［1］。 类似地在制造商与零售商的订购过程中， 为增大订货量制造商也会采取数量折扣［2］。 制造商作为供应链起点， 其决策在系统中扮演着重要角色。 有研究表明， 若原材料的采购成本降低1 个百分点， 中小企业的销量便会相应地提高8个百分点［3］， 因此如何决策数量折扣、 控制采购成本便成为供应链企业需决策的重要问题。 通常数量折扣是指制造商向零售商提供一种与订购量成反比的单位批发价格， 该策略主要应用于薄利多销的行业中， 学术界针对数量折扣的研究也颇为丰富［4，5］。

在供应链环境下， 数量折扣会影响企业利润，也会影响企业制造／再制造的生产计划［6］。 当制造商面对不同类型零售商时， Lau 等［7］给出了制造商的数量折扣框架。 事实上， 自20 世纪80 年代以来， 便有学者认识到数量折扣可以实现供应链协调， 改善供应链的整体绩效［8－12］。 虽数量折扣在渠道协调中得到了广泛应用， 但在零售商竞争时有可能导致渠道成员利润的恶化， 为解决上述问题， 范小军等［13］提出了基于数量折扣及进场费组合的渠道定价策略。 为应对供应链内外环境的变化， 牟宗玉等［14］对数量折扣进行了改进， 从而实现了稳定环境与突发事件下闭环供应链的协调。 刘浪等［15］将供应链系统扩展到了三级供应链系统。 特别地， Rahimi 等［16］在随机市场需求情形下， 发现可利用混合整数非线性规划解决可持续供应链中的折扣问题。 但以上学者在研究数量折扣时， 均忽略了数量折扣及制造商的定价行为将会如何影响下游企业的运转， 亦或数量折扣对下游企业采购行为带来怎样的影响。

近年来， 随着信息技术的快速发展及企业管理水平的不断提高， 催生出了许多新的采购模式，如全球采购、 电子采购、 定制采购及联合采购等，其中联合采购引起了企业和学者的广泛关注。 当存在数量折扣时， 联合采购增强了下游企业的讨价还价能力， 降低了采购成本， 带来了更多盈余。如美国新泽西北部的小型相片冲印商之间的相纸采购联盟Photo Fair Stores， 各成员在加入联盟后其收益均得到了提升。 目前针对联合采购的研究多以定性为主， 只有较少学者进行了定量分析。如刘斌等［17］以短生命周期产品为研究对象， 在应急采购情形下分析了零售商的联合采购策略。 陈敬贤等［18］在线性折扣方案下研究了联合采购对渠道绩效的影响。 当两竞争零售商间存在实力差异时， 王甜源等［19］建立了批量折扣下斯塔克伯格联合采购博弈， 并讨论了联合决策的影响因素。 对于多个零售商形成的联合采购联盟， 肖旦等［20］基于远视结构讨论了联盟的稳定性。 以上学者在研究联合采购策略时， 只与经典的单独采购策略进行了比较， 均没有考虑到竞争零售商间可能会存在的转售行为。 由于受资金、 产品定价及采购能力等方面的约束， 使得部分零售商无法以较理想的批发价格采购产品， 此时转售行为便成为这类零售商降低采购成本、 与其余零售商实现双赢的有效策略。 如加拿大福特汽车零配件制造商采取数量折扣营销策略后， 便出现了部分零售商采购量显著增加而部分零售商采购量显著下降的现象［21］，此时采购量显著增加的零售商将多采购的产品转售给了同一市场的其余零售商， 即制造商实施数量折扣后零售商间出现了转售行为。

基于以上思考， 本文在单制造商与两异质零售商组成的供应链中， 考虑数量折扣下两竞争零售商可能会出现独立采购、 转售行为及联合采购3 种策略。 由于制造商是供应链起点， 其折扣程度及定价行为将会引起零售商层决策的改变， 因此本研究在综合企业间博弈行为、 数量折扣及采购策略的基础上， 建立制造商与两竞争零售商的博弈模型， 尝试分析数量折扣及采购策略带来的影响， 对比3 种采购策略下制造商与零售商的定价及订货水平， 以期为分销渠道成员决策提供理论依据。

总体而言， 通过本研究拟回答以下问题： (1）独立采购、 转售行为及联合采购3 种策略下， 制造商与两竞争零售商将如何决策其定价及订货水平？ (2） 线性量折扣方案及零售商间差异将如何影响渠道成员决策？ (3） 3 种采购策略下制造商及两零售商的利润将如何？

1 问题描述及基本假设

在两层分销供应链中， 为促进销售制造商会实施数量折扣， 假设数量折扣形式为： w=w0－mq［1］， 其中w0表示数量折扣的初始批发价格， 由制造商内生决定； m 表示数量折扣率； q 表示产品订购量。 为降低采购成本， 下游两零售商在进行采购时可能会有3 种不同采购策略， 分别为两零售商独立采购(D）、 两零售商间存在转售(S） 及两零售商联合采购(U）， 具体如图1 所示。

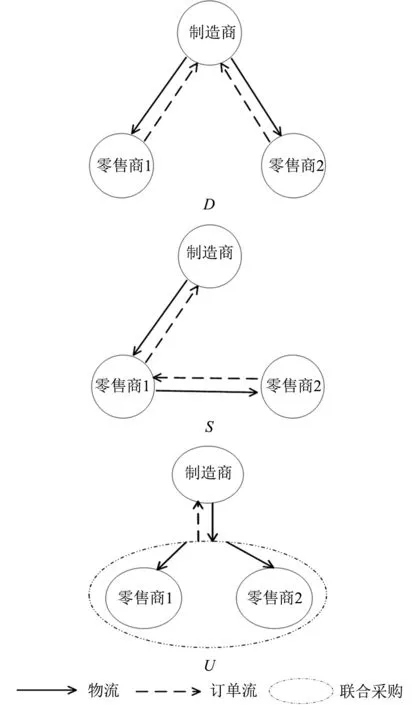
图1 两竞争零售商的3 种采购策略

两零售商的订购量分别为q1和q2， 此时零售市场的产品总量为q0=q1＋q2。 当供需平衡(采购量等于需求量） 时， 产品会以市场出清价进行销售。 设出清价与总订购量间满足线性关系p=aq0［20］(暂不考虑其他因素）， 其中a 为产品市场潜在容量。 因此两零售商间为古诺双寡头竞争，零售商i 的收益Πri=qi(a－qi－qj） (i=1，2）， 其收益不仅与自身订购量qi相关也与竞争对手订购量qj相关。 两竞争零售商的差异主要表现在零售成本方面， 用fi表示零售商i 的单位零售成本， 不妨假设f1＞f2， 即零售商1 的零售成本较高。 本文使用表示采购策略j 下决策主体i 的利润， 上标和下标统一标记如下： i 为z 代表制造商， r1代表零售商1， r2代表零售商2； j 为D 时表示两零售商独立采购， 为S 时表示两零售商间存在转售，为U 时表示两零售商联合采购； c 表示单位产品生产成本。

2 不同采购策略下的博弈模型

本节分别在独立采购(D）、 转售行为(S）及联合采购(U） 3 种采购策略下， 建立制造商与两竞争零售商的博弈模型。

2.1 两零售商独立采购（D）

两零售商独立采购代表了一类采购策略， 在该采购策略下制造商处于主导地位， 两零售商作为追随者且同时决策以实现自身利润最大化， 因此制造商与两零售商间进行的是两阶段动态博弈，具体博弈顺序是： (1） 制造商先决策初始批发价格w0； (2） 两零售商观察到制造商决策后再同时决策产品订购量q1和q2， 该问题可以抽象为一个双层优化模型：

采用逆向归纳法求解上述模型， 当m＜1 时最优初始批发价格及最优订购量分别为：

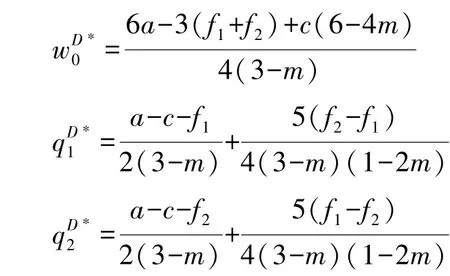
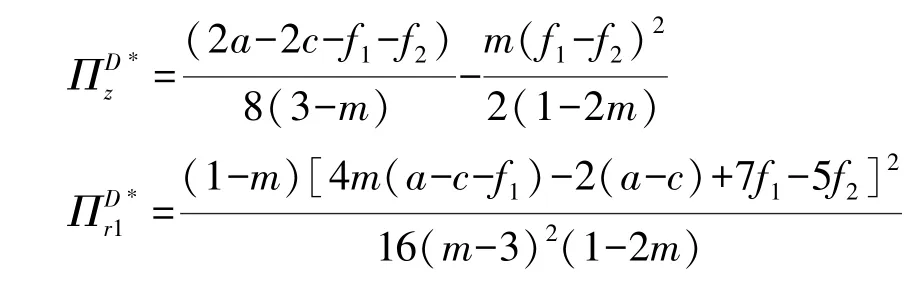
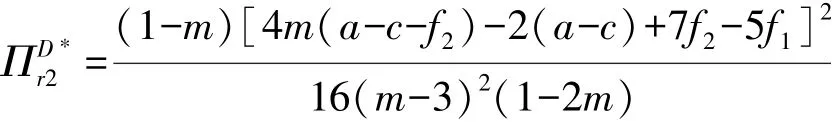
2.2 两零售商间存在转售行为（S）

引理1： 当两零售商间存在转售行为时， 是零售成本较高的零售商将产品转售给零售成本较低的零售商， 即零售商1 将产品转售给零售商2。

证明： 采用反证法证明， 记两零售商间的转售价格为ps， 假设零售商2 将产品转售给零售商1。 对零售商1 而言， 单位产品的销售利润须大于转售价格即p－f1＞ps； 又因为f1＞f2， 因此对零售商2 也一定存在着单位产品的销售利润大于转售价格即p－f2＞ps。 当销售收益高于转售获得的收益时， 理性的零售商2 会选择将产品直接销售到市场， 而不会将产品转售给零售商1， 因此假设不成立， 引理得证。

两零售商间存在转售行为时， 制造商作为主导者仍优先决策， 其次是零售商1 决策， 最后是零售商2 再决策， 因此制造商与两零售商间进行的是三阶段动态博弈， 博弈顺序为： (1） 制造商决策初始批发价格w0； (2） 零售商1 决策产品订购量q1及产品转售价格ps； (3） 零售商2 决策其从零售商1 处订购的产品量q2， 该问题可以抽象为一个三层优化模型：

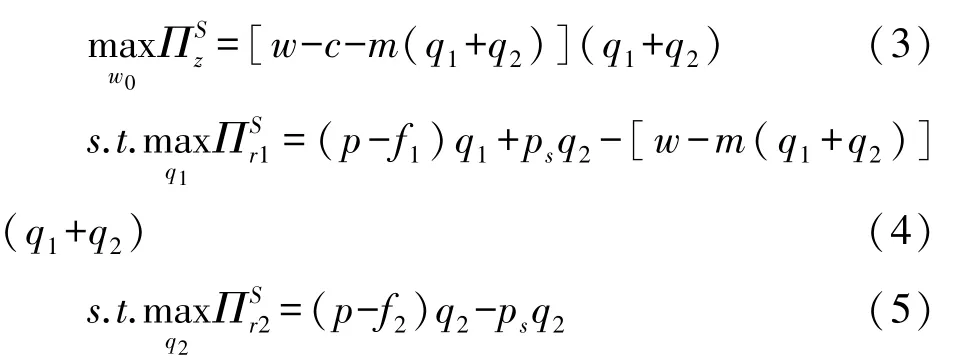
仍采取逆向归纳法求解， 求得最优初始批发价格、 两零售商的最优产品订购量分别为：

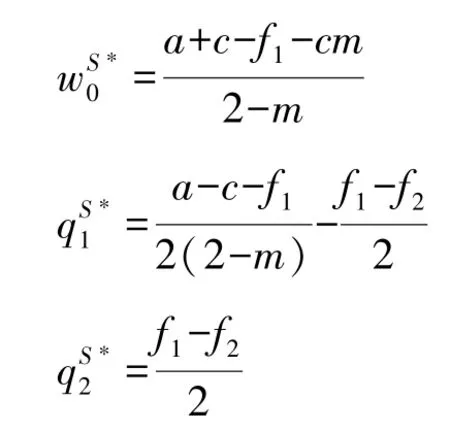
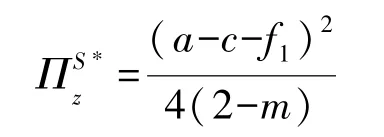
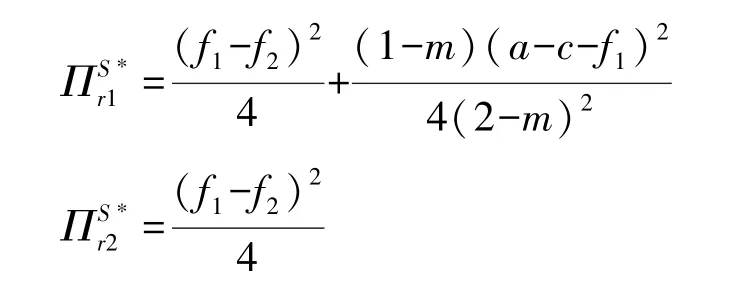
2.3 两零售商联合采购（U）

为降低采购成本， 享受更多数量折扣， 下游两零售商可能采取汇集双方采购量的方式进行联合采购， 即两零售商实施采购联盟将双方需求进行汇集然后统一从制造商处进行采购， 同时在零售市场上两者仍保持竞争关系。 两零售商联合采购时， 制造商与采购联盟之间进行的是两阶段动态博弈， 博弈顺序为： (1） 制造商先决策初始批发价格w0； (2） 采购联盟依据双方市场需求确定产品采购量q1＋q2， 该问题可以抽象成一个两层优化模型：

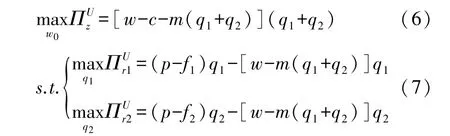
仍采取逆向归纳法求解， 得最优初始批发价格及最优订购量分别为：

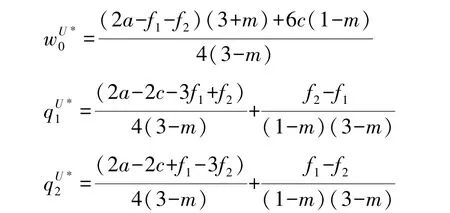
3 采购策略对供应链均衡结果的影响

为分析采购策略对竞争供应链均衡结果的影响， 将3 种采购策略下的决策及利润进行比较并分析， 可得如下性质(分别对、、作差， 再与0 比较即可得证， 其余证明类似）。 本文将两零售商的零售成本之差记为Δ， 即Δ=f1－f2， 其值可衡量两零售商间的差异， 其值越低说明两零售商的差异越小， 反之则越大。

3.1 采购策略对供应链均衡决策的影响

性质1： 3 种采购策略下制造商初始批发价格大小关系：

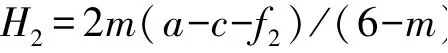
性质1 表明， 无论产品数量折扣率是高或低，两零售商联合采购(U） 时初始批发价始终大于独立采购(D） 时的取值。 相比与独立采购(D），联合采购(U） 时零售商层获得了更多数量折扣，一定程度上降低了零售商层的采购成本， 为保证较高利润， 此时上游制造商会选择制定较高的初始批发价格。 特别地， 在转售行为(S） 下， 零售商2 从零售商1 处订货， 然后零售商1 再从制造商处订货， 即只有零售商1 可直接享受到数量折扣， 此时制造商初始批发价格的相对大小则与两零售商成本之差Δ 相关。 当Δ＜H1时转售行为下初始批发价格可达到最大， 当H1＜Δ＜H2时转售行为下初始批发价格居中， 当Δ＞H2时转售行为下初始批发价格会跌至最小。 由此看出， 转售行为(S） 下两零售成本之差越大， 制造商制定的初始批发价格会越低。 这意味着下游零售商间的差异会直接影响上游制造商的定价水平。

性质2： 3 种采购策略下零售商1 的订货水平：

当数量折扣率0 ＜m ＜1/2 时， 若Δ ＜H3， 则

若Δ＞H4， 则

若H3＜Δ＜H4， 则当1/2＜m＜1 时， 若Δ＜H3， 则

若Δ＞H3， 则

2.炒锅置火上，放菜油烧至四成热，下干辣椒节炒几下，再下牛油炒热放豆瓣酱炒香，下姜片、蒜片，炸出香味，倒入鲜汤，用大火烧沸，下醪糟汁、精盐、冰糖，熬 10 min，下花椒熬出香味，舀入火锅中，打去浮沫，加入味精，即为汤汁。火锅点火，放入红枣、猪蹄块、蹄筋煮沸，便可随意烫食。

其中： H3=2(2m－1）(a－c－f1）/(4m3－22m2＋29m－2）

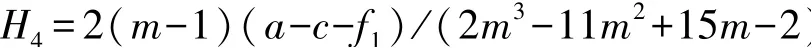
性质2 表明， 若制造商的数量折扣率较低(0＜m＜1/2）， 独立采购(D） 时零售商1 的订货量始终小于联合采购(U） 时的取值。 由于零售商1 的零售成本较高， 在联合采购时可享受到更多数量折扣， 因此联合采购下会相对增大其产品订购量。 而在转售行为(S） 下， 零售商1 订货量的相对大小则与两零售成本之差及阈值(由市场潜在容量a、 产品生产成本c 及两零售商的零售成本f1、 f2组成） 取值相关。 当Δ＞H4时， 转售行为下零售商1 的订货量达到最高， 当H3＜Δ＜H4时转售行为下零售商1 的订货量居中， 在Δ＜H3时转售行为下零售商1 的订货量最低。

若制造商的数量折扣率较高(1/2 ＜m ＜1），与独立采购(D）、 转售行为(S） 相比， 联合采购(U） 时零售商1 的订货量反而最低。 这是因为数量折扣率越高时， 虽订购量越大产品批发价格会越低， 但考虑到产品以市场出清价格进行销售， 过多的订购量会降低产品零售价格， 因此当产品数量折扣率较高时， 联合采购(U） 下零售商1 反而会降低其订货量。 而独立采购(D） 及转售行为(S） 下， 零售商1 订货量的相对大小则与两零售成本之差及阈值取值相关。 在满足条件Δ＜H3时， 独立采购时零售商1 的订购量较大，在满足条件Δ＞H3时， 转售行为下零售商1 的订购量较大。

性质3： 零售商2 的订货水平：

当数量折扣率0＜m＜1/2 时， 若Δ＞H5且Δ＞H6， 则

若Δ＜H5， 则

若H5＜Δ＜H6， 则

当1/2＜m＜1 时， 若Δ＞H5， 则

若Δ＜H6， 则

若H6＜Δ＜H5， 则

其中： H5=［2(2m－1）(a－c）＋f1＋f2－4mf1］/(10m－4m2）

由性质3 可知， 若制造商的数量折扣率较低(0＜m＜1/2）， 联合采购(U） 时零售商2 的订货量始终小于独立采购(D） 时的数值。 而转售行为(S） 时零售商2 订货量的相对大小也与两零售商成本之差及阈值取值相关。 当Δ＞H5且Δ＞H6时，转售行为下零售商2 的订货量最低， 在H5＜Δ＜H6时转售行为下零售商2 的订货量居中， 在Δ＜H5时转售行为下零售商2 的订货量可以达到最高。

若制造商的数量折扣率较高(1/2 ＜m ＜1），独立采购(D） 时零售商2 的订货量始终小于联合采购(U） 时的数值， 而转售行为(S） 时零售商2 订货量的相对大小也与两零售商成本之差及阈值取值相关。 当Δ＞H5时， 转售行为下零售商2 的订货量最低， 当H6＜Δ＜H5时转售行为下零售商2 的订货量居中， 当Δ＜H6时转售行为下零售商2 的订货量可以达到最高。

当制造商的初始批发价格及数量折扣率在不同区间范围时， 下游竞争性零售商的订货决策也会随之发生改变。 通过比较性质2 和3， 还可发现在一定条件下两零售商会采取相反的订货策略。这是因为在零售市场上， 两零售商是完全竞争关系， 当一方订货水平较高时会限制另一方的订货水平， 否则会因为总订货量上升导致产品市场出清价格下降， 从而使得利润也下降。 因此两零售商在决策订货水平时， 不仅需要考虑制造商的初始批发价格及数量折扣率， 也需兼顾竞争对手的订货策略。 如制造商的数量折扣率较低(0＜m＜1/2）， 独立采购(D） 时零售商1 的订货量始终小于联合采购(U） 时的取值， 而此时零售商2的订货策略却相反， 独立采购(D） 时零售商2的订货量却始终大于联合采购(U） 时的取值。

性质4： 3 种采购策略下， 独立采购(D） 与联合采购(U） 时两零售商的总订购量相等且均大于转售行为(S） 下的取值， 即

在两零售商联合采购(U） 时， 零售商层获得了较多数量折扣。 由于制造商可通过初始批发价格及数量折扣两种方式调控采购成本， 此时制造商为实现利润的最大化， 会相应地提高初始批发价格， 从而又间接地提高了采购成本， 这样又会降低零售商层的采购意愿， 最终使得联合采购(U） 与独立采购(D） 时两零售商的总订购量相等。 当两零售商间存在转售行为(S） 时， 零售成本较大的零售商1 为获得更多数量折扣选择多订购产品， 然后再将产品销售给零售商2， 零售商间的转售行为仅使零售商1 获得了数量折扣，而零售商2 没有直接享受到数量折扣， 因此降低了其采购的积极性， 最终导致转售行为下零售商层的总订购量较小。

3.2 采购策略对供应链均衡利润的影响

性质5： 不同采购策略下制造商利润大小满足：

若H7＞0，

若H7＜0， 则

其中： H7=(2－m）［(2a－2c－f1－f2）2(1－2m）2－4m(3－m）Δ2］－2(3－m）(1－2m）2(a－c－f1）2

由性质5 可知， 无论阈值取值大或小， 两零售商联合采购(U） 时制造商利润会达到最高。这是因为与独立采购(D） 相比， 联合采购(U）时制造商可以制定相对较高的初始批发价格， 由于联合采购(U） 与独立采购(D） 时零售商层的总订购量相等， 因此使得联合采购(U） 时制造商的利润相对较高； 而在两零售商间存在转售行为(S） 时， 虽制造商在一定阈值范围内也可制定较高的初始批发价格， 但由于其部分利润被零售商1 剥夺， 最终使得转售行为(S） 时制造商的利润仍低于联合采购(U） 时的取值， 因此对上游制造商而言， 其总是会倾向于两零售商采取联合采购策略(U）。 同时独立采购(D） 与转售行为(S） 下制造商利润的相对大小则与阈值H7相关， 当H7＞0 时独立采购(D） 下制造商的利润大于转售行为(S） 下的取值， 否则相反。

同样地， 当系统参数属于不同阈值区间时，两零售商的利润满足如下：

性质6： 对零售商1 而言：

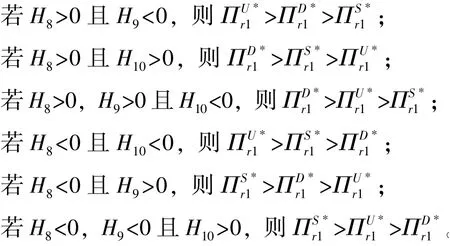
对零售商2 而言：

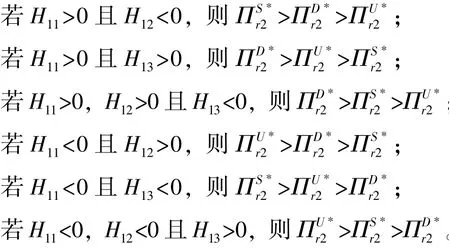
其中： H8=(1－m）(2－m）2［2(a－c－f1）(1－2m）－5Δ］2－4(m－3）2(1－2m）2［Δ2(2－m）2＋(1－m）(a－c－f1）2］

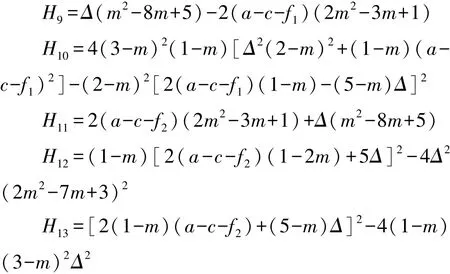
通过性质6 可知， 当H8＞0 时， 独立采购(D）下零售商1 的利润大于转售行为(S） 下的取值，而联合采购(U） 下利润的相对大小则与阈值相关， 当H9、 H10在不同区间范围时， 联合采购(U）下零售商1 利润或最大或居中或最小； 当H8＜0时独立采购(D） 下零售商1 的利润小于转售行为(S） 下的取值， 而联合采购(U） 下利润的相对大小也与阈值H9、 H10取值相关。

类似地， 当H11＞0 时， 独立采购(D） 下零售商2 的利润大于联合采购(U） 下的取值， 而转售行为(S） 下利润的相对大小则与阈值H12、H13取值相关； 当H12、 H13在不同区间范围时， 转售行为(S） 下零售商2 利润或最大或居中或最小； 当H11＜0 时独立采购(D） 下零售商2 的利润小于联合采购(U） 下的取值， 同样地， 转售行为(S） 下利润的相对大小也与阈值H12、 H13取值相关。 因此对于两竞争且异质零售商而言，均不存在某一采购策略严格优于其余采购策略的情形， 当阈值在不同区间范围时3 种采购策略均有可能使其利润达到最大。

4 数值仿真

本节将通过数值算例比较3 种采购策略下制造商的定价、 两竞争零售商的订货水平及相应的利润获取情况， 以期为供应链成员决策提供依据。由于竞争供应链系统中参数取值需满足博弈模型的演算条件， 如需满足制造商及两零售商利润函数的凹性等要求， 因此将系统参数取值如下： a=100， c=2， f1=12， f2=4， m=0.2。 基于以上系统参数赋值， 可求得3 种采购策略下供应链成员的最优决策及利润， 具体见表1。

表1 3 种采购策略下两零售商的决策及利润

当系统参数(数量折扣率m、 市场潜在容量a、 产品生产成本c 及两零售商零售成本f1、 f2）属于不同阈值区间时， 3 种采购策略下初始批发价格、 两零售商订货量及供应链成员利润的相对大小会发生改变， 此时满足Δ ＞H2， Δ ＞H4， Δ ＞H5， Δ＞H6， H7＞0， H8＜0， H9＜0， H10＞0， H11＞0，H13＞0， 因此有。 即制造商初始批发价格在联合采购(U） 策略下制定的最高为53.43， 此时其利润也达到最大为1446.43； 零售商1 的订货量在转售行为(S） 下达到最高为19.89， 此时其利润也达到最大为472.54； 而零售商2 却是在独立采购(D） 下订货量达到最大为22.74， 此时其利润也达到最大为413.62； 同时独立采购(D） 及联合采购(U）策略下零售商层的总订货量相等均为32.14， 显著大于转售行为(S） 时零售商层的总订货量23.89，因此在上述参数赋值情形下， 制造商会倾向于两零售商采取联合采购(U） 策略， 零售商1 会倾向于采取转售行为(S）， 而零售商2 则倾向于采取独立采购(D） 策略。

5 结 论

本文在单制造商与两竞争零售商构成的分销供应链中， 考虑到实施数量折扣后， 下游两异质零售商可能采取独立采购(D）、 转售行为(S）及联合采购(U） 3 种策略。 然后运用博弈论及最优化理论， 分析并对比了3 种采购策略下渠道成员的定价、 订货及利润水平， 以期为渠道成员的决策提供理论依据。 结果表明：

(1） 与独立采购(D） 相比， 两零售商联合采购(U） 时无论数量折扣率是高或低， 制造商均可制定相对较高的初始批发价格； 而转售行为(S） 下虽只有零售商1 直接享受数量折扣， 但制造商不可盲目地抬高或降低初始批发价格， 其大小须依据两零售商间的差异而定， 两零售商的销售成本之差越大， 制造商越应降低初始批发价格。

(2） 两零售商在决策订货水平时， 不仅需考虑初始批发价格及数量折扣率， 也需兼顾竞争对手的订货策略。 联合采购(U） 时虽零售商享受了较多的数量折扣， 但制造商相应地提高了初始批发价格， 最终使得联合采购(U） 与独立采购(D） 时总订购量相等且均大于转售行为(S） 下的取值。

(3） 无论数量折扣率是高或低， 亦或阈值取值是大或小， 两零售商联合采购(U） 时制造商利润可以达到最大。 即联合采购情形下的博弈策略是制造商的严格上策。 对两竞争零售商而言，均不存在某一采购策略严格优于其余采购策略的情形， 当阈值在不同区间范围时3 种采购策略均有可能使其利润达到最大。

本文尝试在分销供应链中研究采购策略对渠道成员定价、 订货及利润的影响， 以期更好理解企业间的博弈策略。 尽管如此， 仍存在若干局限，今后可考虑拓展到非对称信息等情形。