有限元极限平衡法与强度折减法在边坡稳定性分析中的对比
杨正玉,刘顺青 ,崔 雨
(1.江苏省地质矿产局第三地质大队,江苏 镇江212001;2.江苏科技大学 土木工程与建筑学院,江苏 镇江212005)
我国是一个多山的国家,每年滑坡等地质灾害频发,由此而导致的损失十分严重。在进行滑坡灾害治理时,合理的边坡稳定性评价十分重要。
目前边坡稳定性分析方法主要有2类。第一类为极限平衡法,代表性的有瑞典法[1]、Bishop法[2]、不平衡推力法[3]、摩根斯坦-普莱斯方法[4]等,这些方法能较快地给出边坡的稳定安全系数,比较受工程师青睐。第二类方法为有限元法,包括有限元强度折减法[5]及有限元极限平衡[6],这两类方法在相同边坡模型中的计算精度还缺乏系统研究。
本文基于有限元极限平衡法和强度折减法,重点对比分析澳大利亚计算机应用协会(ACACD)所使用的边坡稳定性考题,用于定量评价这两种有限元法的计算精度。研究结果对提高边坡稳定性的计算精度具有重要意义。
1 基本原理
1.1 有限元极限平衡法
有限元极限平衡法是有限元与极限平衡两种方法的结合。该方法在分析边坡稳定性时,首先利用有限元静力分析求得边坡内的应力应变分布,然后将计算结果通过应力张量变换,求出土条底部的应力,最后根据极限平衡法求得边坡的安全系数。对平面应变问题,首先根据有限元法求得应力场,而后根据摩尔-库伦准则求得相应条块底部的抗剪强度,如图1。
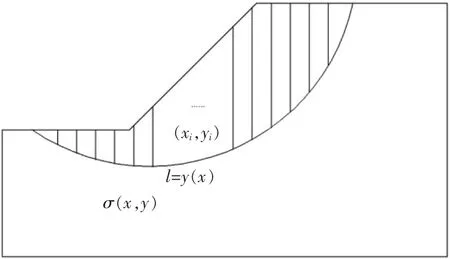
图1 有限元极限平衡法土条受力
假定曲线l为任意一条滑动面,l的方程为l=y(x),则此时边坡的安全系数定义为:

式中 τf为沿滑动面的抗剪强度;τ为沿滑动面的剪应力。
1.2 有限元强度折减法
有限元强度折减法中边坡稳定的安全系数定义为:使边坡刚好达到临界状态时,对岩、土体的抗剪强度进行折减的程度[7]。该方法的基本原理是将边坡土体强度参数黏聚力c和内摩擦角φ同时除以一个折减系数F,得到一组新的强度参数,再进行试算,直至边坡达到极限平衡状态为止,此时对应的折减系数F,即为边坡的安全系数。经过折减后,边坡土体的强度参数c′和φ′,如式(2),式(3):

2 算例分析
本文采用澳大利亚计算机应用协会(ACADS)所采用的边坡稳定性考题[8]对有限元极限平衡法及强度折减法的计算精度进行验证。
2.1 算例1
一均质边坡,其几何模型如图2,材料特性参数如表1。
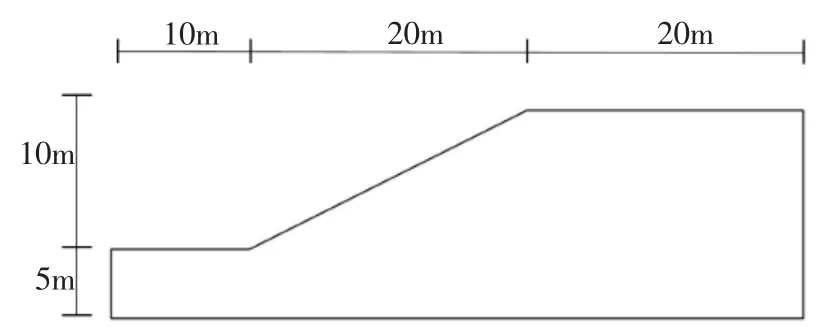
图2 边坡几何模型

表1 算例1边坡土体参数
本文采用Midas GTS NX分析边坡稳定性,有限元的网格尺寸大小为0.5m,计算模型采用摩尔-库伦模型。边坡稳定性计算结果如表2。

表2 边坡稳定性计算结果
从表2可看出,对于均质边坡,有限元强度折减法计算所得的安全系数比有限元极限平衡法的稍大。有限元极限平衡法与Bishop及Janbu法相比,边坡稳定安全系数分别增大2.0%,3.6%;有限元强度折减法与Bishop及Janbu法相比,边坡稳定安全系数分别增大8.8%,10.5%。
2.2 算例2
一多层土边坡,其几何模型如图3,材料特性参数如表3。
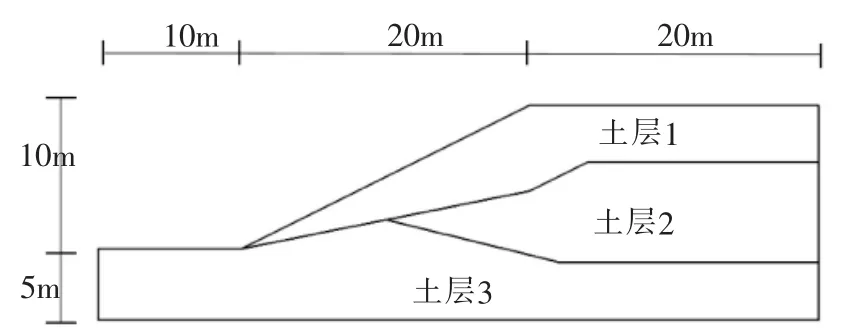
图3 边坡几何模型

表3 边坡土体参数
采用Midas GTS NX分析边坡的稳定性,有限元的网格尺寸大小为0.5m,计算模型采用莫尔-库伦模型。边坡稳定性计算结果如表4。

表4 算例2边坡稳定性计算结果
从表4可看出,对于多层土边坡,有限元强度折减法计算所得的安全系数大于有限元极限平衡法计算所得。有限元极限平衡法与Bishop法相比,边坡稳定安全系数减小了0.5%,与Janbu法相比,安全系数增大了4.4%; 有限元强度折减法与Bishop及Janbu法相比,边坡稳定安全系数分别增大4.3%,9.4%。
2.3 算例3
一含软弱夹层的边坡,其几何模型如图4,材料特性参数如表5。
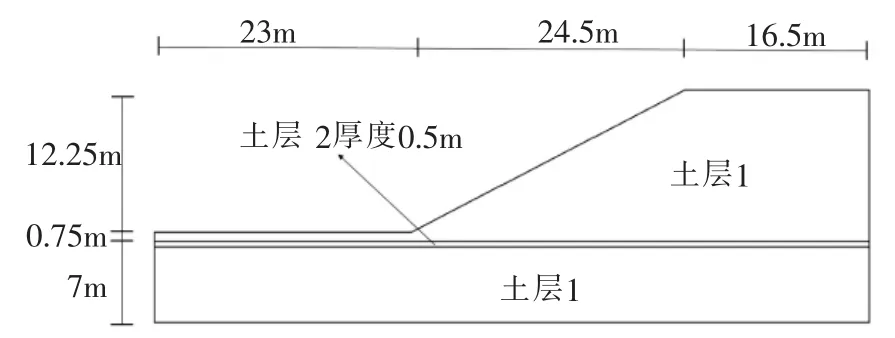
图4 边坡几何模型
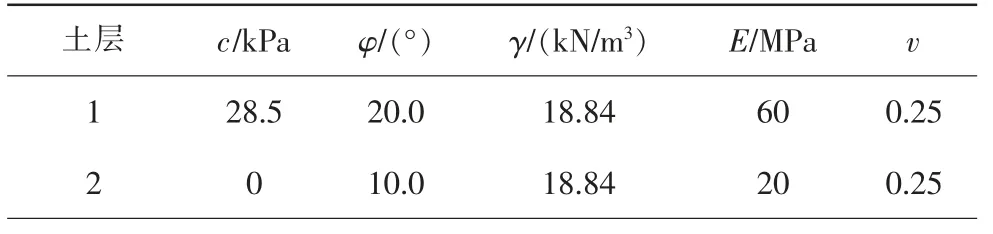
表5 边坡土体参数
本文采用Midas GTS NX分析边坡的稳定性,有限元的网格尺寸大小为0.5m,计算模型采用莫尔-库伦模型。边坡稳定性计算结果如表6。

表6 边坡稳定性计算结果
从表6可看出,对于含软弱夹层边坡,有限元强度折减法与其他方法计算所得的安全系数差别较大,该方法计算所得的安全系数明显偏小,此时边坡等效塑性应变云图如图5,从图5可见边坡的潜在滑动面穿过软弱夹层。有限元极限平衡法与Bishop及Janbu法计算所得的安全系数比较接近。

图5 基于强度折减法的边坡等效塑性应变云图
为了验证此时有限元强度折减法计算所得结果的合理性,采用极限分析程序Optum G2对算例3进行稳定性计算,计算时采用强度折减极限分析法,计算所得的边坡下限安全系数为1.251,上限安全系数为1.295,可见采用Midas GTS NX中的强度折减法分析所得边坡稳定安全系数的结果是合理的。
3 结语
(1)对于均质及多层土边坡,有限元极限平衡法与强度折减法的计算结果较为接近,两种计算方法与Bishop及Janbu法的误差在10%以内。
(2)对于含软弱夹层的边坡,有限元强度折减法计算所得的安全系数明显偏小; 而有限元极限平衡法与Bishop及Janbu法计算结果较为接近。

