支座处可滑动的多跨连续索分析与计算

王 伟，黄才良

(大连理工大学 土木工程学院 大连市 116023)

悬索结构以其造型美观等优点而在工程中的应用日益广泛，而多跨连续索在支座处的滑移问题在悬索桥吊装系统以及矿山索道等工程中经常遇到，文献[1]针对上述问题提出过索的变原长计算模式，但仅能求解索端部张力已知的情况。文献[2]利用五节点曲线索单元基本方程,建立了滑移索单元非线性迭代计算模式，但计算量较大。文献[3]提出了一种在索段原长已知的情况下求解在中间节点处可自由滑动的多跨连续索静力平衡的方法。现有的参考文献大多仅对索段进行分析，对施工过程涉及较少。

对缆索在支座处可自由滑动的多跨连续索静力平衡进行了分析，提出了已知目标点标高求缆索线型以及已知主索无应力长度求解施工过程线形两种计算模式。以张家口市尚义县大青山人行玻璃悬索桥施工过程为背景，对缆索吊装系统架设控制进行了详细分析，该算法在实际工程应用中，具有计算速度快，精度高等特点。

1 计算假定

分析中采用了以下4个基本假设：

(1)索的材料符合虎克定律，即在正常情况下，索的应力与应变呈线性关系；

(2)索为理想状态下柔性索，仅承受拉力，既不能受压也不能受弯；

(3)索因受力引起的横截面积改变量忽略不计；

(4)不计摩擦影响。

2 悬链线基本方程

如图1所示的柔性索段ij，弹性模量为E，横截面积为A，均布荷载集度为q；Hi、Hj与Vi、Vj以及Ti、Tj分别为i、j两端的水平力、竖直力以及切线张力；l、h为索段i、j两端的跨度与高差；索段无应力长度S0，变形后形状长度为S，可得悬链线基本方程[4]:

(1)

如图2所示，均布荷载与集中荷载作用下悬索相当于n个基本索段组合在一起，并且在索段间节点处有集中力Pi，悬索满足如下力学条件：

(2)

3 已知控制点坐标求线形

3.1 悬索线形变化刚度

对式(1)取微分得[5]，

(3)

将式(3)离散化，

(4)

可以得到

(5)

上式表达了一夸悬索的线形(跨度和高差)变化量与内力变化量之间的关系，即为水平力与竖直力迭代初值的修正公式。

3.2 主跨缆索迭代步骤

(6)计算了缆索末端点以及控制点计算标高与指定标高误差：

(6)

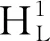
3.3 边跨索力修正公式

对式(1)微分可得

(7)

对于成桥状态边跨某一索段来说，dli=0，常规悬索桥主缆计算时，中跨在支座处水平分力已知，边跨与中跨水平力平衡，即dHi=0，只需调整竖向力即可，对于在支座处可滑动的连续索，边跨控制目标为与主跨拉力相等，此时只需给定水平力Hi或Vi中任意一个，即可确定另一个分力，因此仍可假设其水平力为定值，即dH=0，则

(8)

将式(8)中两式合并，得

(9)

dVi=Di·dhi

(10)

其中Di即为索段索力的修正刚度，从而可得边跨主索累计总变化量

(11)

3.4 边跨缆索迭代步骤

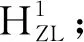
4 已知主缆无应力长度求缆索线形

4.1 已知无应力长度求外加荷载时主缆线形

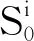
4.2 主索滑移刚度确定

4.3 滑移量计算

4.4 迭代计算流程

(1)按照3.2主跨主缆计算方法，将A、B、C、D均固定，可得到AB段B端拉力TAB-B、BC段两端拉力TBC-B与TBC-C以及CD段C端拉力TCD-C；

(2)利用3.1计算AB、BC、CD段滑移刚度；

(3)按照4.2对AB、BC段无应力长度进行调整；

(4)根据调整后AB、BC段的无应力长度重新计算两端拉力，直到两端拉力差值|TBC-B-TAB-B|≤ε，否则重新计算两段刚度，重复②③步骤，直到满足精度要求；

(5)对BC、CD段重复上述(2)(3)(4)步骤，直到满足精度要求；

(6)此时各段拉力必然发生变化，重新计算各段拉力，判断是否满足精度要求，不满足则重复上述迭代过程，直到满足为止，此时的缆索线形即为所求连续式缆索线形。

5 算例验证

张家口人行吊桥工程位于张家口尚义县大青山森林公园景区，距离张家口市区87km，距离北京市区236km。本项目为景区的人行桥，大致为南北走向，桥梁结构的选择在满足基本功能的同时，还应注重景观效果。本桥连接两侧山脊，桥梁跨度为445m，桥跨间最大沟谷深度约120m，桥梁有效通行宽度2.4m，桥面采用玻璃铺装。本桥采用单跨地锚式钢桁架悬索桥结构形式，结构轻盈、桥型美观。主梁为钢桁架，主桁标准阶段重5t，索塔为钢筋混凝土结构，南侧塔高52.13m，北侧塔高43.74m。主跨跨度为445m，成桥状态下理论矢高为37.5m，矢跨比为1/11.87。全桥设有65对竖向吊杆，顺桥向吊杆间距为6.66m，横桥向吊杆间距为3.6m。

该桥利用缆索吊装系统将主桁标准段从北塔处向跨中运送拼装，在拼装过程中由于吊装重量，缆索吊装系统必将下降，因此要保证主桁标准段在运送过程中缆索吊机始终不能与主缆碰撞，所以要计算运送过程中吊装系统各点标高，找到各点距主缆的最低点，同时随着主桁架的拼装，主缆线形也将随之改变，因此也要找到主缆最不利位置。

根据计算结果，天缆在吊装主桁标准段时，与主缆之间高差最小为0.268m，天缆在主缆之上，缆索吊机可以顺利通过，利用编写的连续式缆索计算程序所得结果，理论计算标高与实测标高误差最大为11mm，在工程允许范围内。

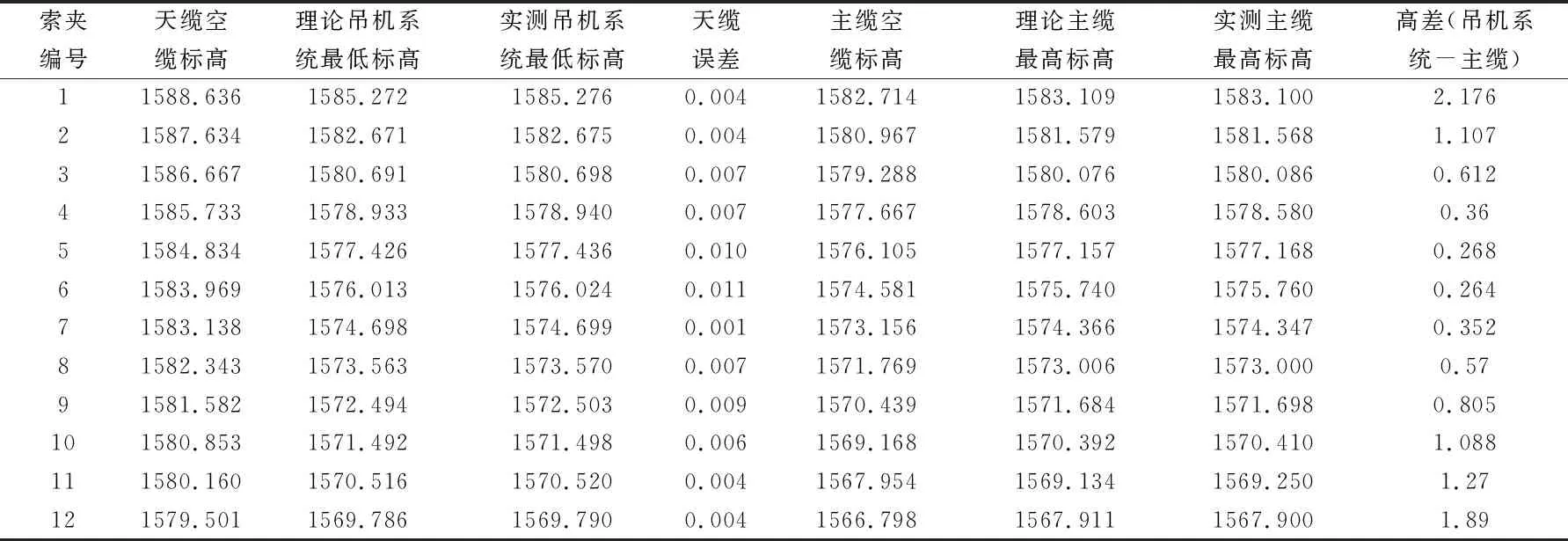
表1 吊装系统与主缆标高

6 结语

(1)利用分段悬链线理论得到连续式缆索系统线形的解析解，计算精度较高，解决了目前其他软件没有涉及的主索在索鞍处可以自由滑动的线形问题；

(2)对连续式可滑动缆索系统的两种情况进行讨论，即已知目标点标高求缆索线形和已知空缆线形求施加荷载后线形问题，经过算例验证，该求解方法具有迭代速度快，求解精度高的特点；

(3)该计算程序运用在张家口市尚义县大青山人行玻璃吊桥的施工过程中，取得了圆满成功，对缆索吊机系统、猫道系统以及吊装过程中的线形控制达到了较高水平，保证了施工顺利进行。