随机需求下定制公交站点及路径动态优化模型
魏长钦, 王伟智
(福州大学土木工程学院, 福建 福州 350108)
0 引言
定制公交作为常规公交的补充, 在20世纪70年代, 美国开始出现定制公交, 而国内直到2013年才开始出现定制公交, 并迅速在各大城市普及. 国外对定制公交站点和线路的规划研究较早. BADIA等[1]以放射型路网城市为研究对象, 引入单一覆盖区域站点, 将中心区域大小、 车头时距以及停车间距等作为决策变量, 以运营费用和乘客费用最低为目标规划公交线路. TONG等[2]从时空网络建模的角度出发, 建立基于多商品网络流的优化模型, 在满足时间窗定义的个体需求同时, 优化公交车的利用率. LYU等[3]提出一种同时优化公交站点位置、 线路、 时刻表和乘客选择定制公交概率的数学规划公式, 并建立启发式的解决方案框架来最大化估计利润.
国内在定制公交方面的研究主要采用聚类算法对需求进行聚类进而设站, 按照一定优化目标和约束建立线路优化模型, 通过蚁群、 遗传等启发式算法进行求解. 马继辉等[4]利用层次聚类法, 对出行需求进行聚类, 划分起、 终点区域, 并将起终点区域又分别划分为7个小站点区域作为停靠站点; 雷永巍[5]采用K-mean算法对居民的实时出行需求进行聚类, 设计基于Hadoop平台的并行蚁群算法对双层路径规划模型进行求解; 王健等[6]利用合并思想, 将距离小于500 m的站点合并, 两者中点作为新站点, 以最短里程为寻优目标, 利用贪心-遗传算法进行求解. 在动态车辆路径问题上, 吴升等[7]考虑了影响移动物流车辆优化调度的各种随时间变化的动态参数, 提出基于混合遗传算法的动态VRP求解策略.
目前研究还存在一定不足, 公交站点的设置多为聚类后的虚拟站点, 并未考虑实际站点的特性及实际交通因素, 且缺乏有效的站点筛选模型. 本研究在公交站点的基础上, 针对每站点0~5个随机需求, 综合考虑定制公交服务率和动态行程时间, 以最大载客量、 运营成本、 行程时间为约束, 建立随机需求下定制公交动态路径优化模型, 并以改进的A*算法求解得到动态路径.
1 定制公交站点重要度评估模型
1.1 复杂网络与道路交通网络
道路网络是由道路和节点组成的无标度复杂网络系统, 具有小世界特征. 王锋等[8]基于无向无权复杂网络理论, 提出基于m阶邻居节点重要度贡献的节点重要度评估方法. 本文利用复杂网络理论对交通网络中节点重要度进行评估, 筛选出重要站点, 供路径寻优时选择停靠.
复杂网络研究常用对偶拓扑方法, 将路段映射为节点, 交叉口映射为边, 建立对偶拓扑结构模型. 本文借鉴此法, 通过路段与站点“对偶转换”, 得到新的网络拓扑结构.
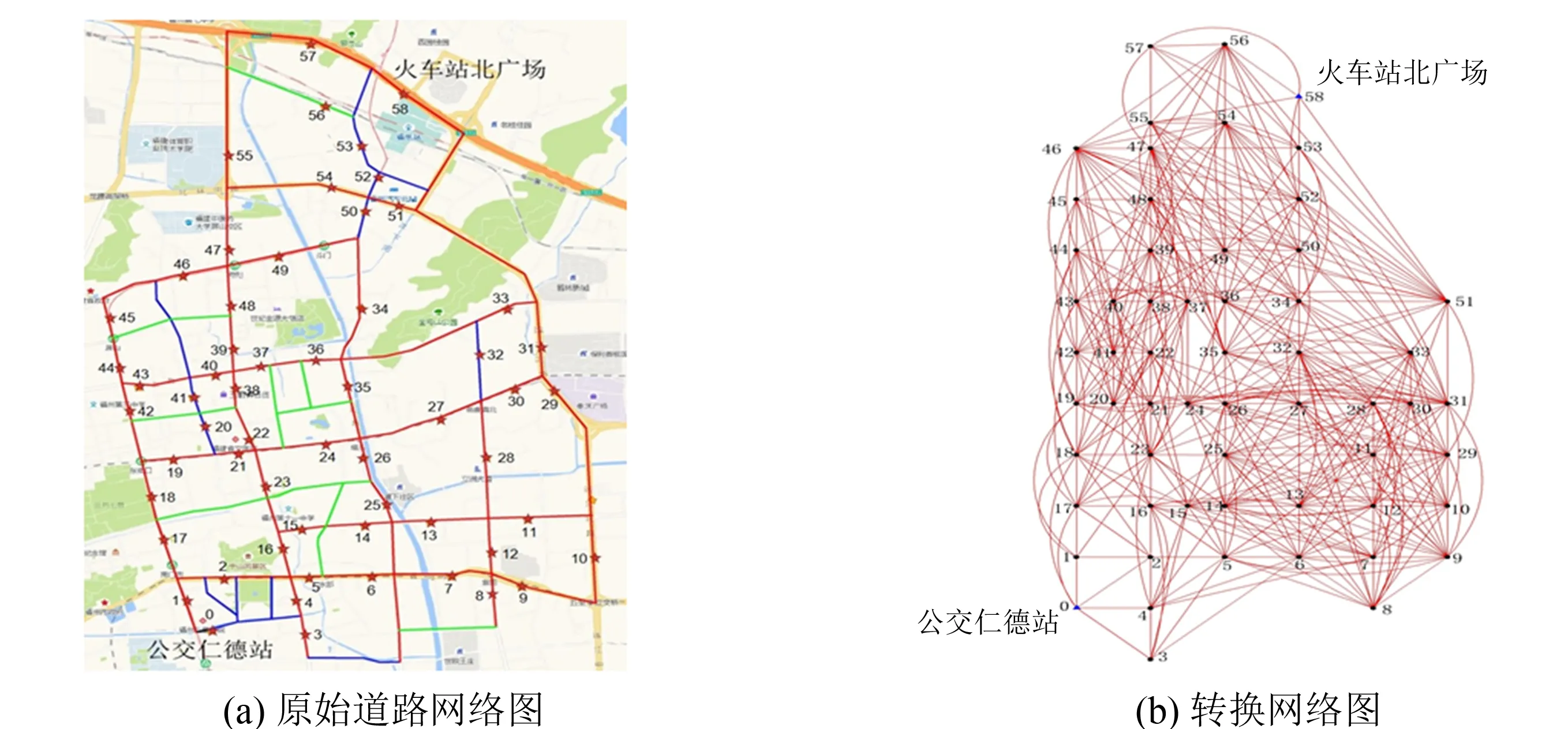
将公交站点视为网络节点(图中以符号“·”表示, 数字编号1、 2、 …为其站点编号), 各站点间的连接段视为网络的边, 边上(x1,x2,x3,x4)四个数字分别指代道路等级(0为主干道, 1为次干道, 2为支路)、 站点距离(m)、 相隔交叉口个数、 下一站点随机需求数. 在图1(a)中, 红色线段为主干道、 蓝色为次干道、 绿色为支路, 且两站点间经过多个道路等级, 按低等级计算. 路网转换前后结构如图1(b)所示.
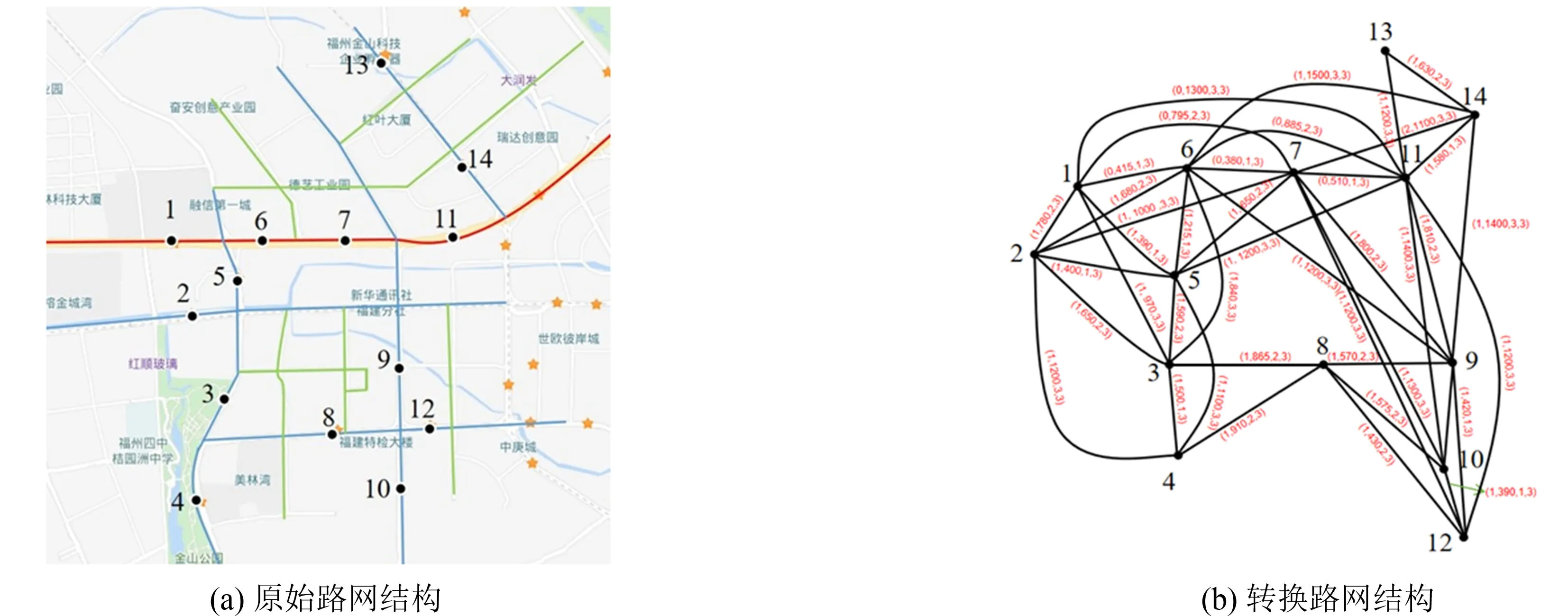
图1 路网转换前(后)拓扑结构Fig.1 Topology before (after) road network conversion
1.2 道路网络节点重要度评估
复杂网络中常用节点重要性等价于节点显著性的方法来判别节点重要度, 节点度是节点显著性指标之一, 指连接该节点与之相关联的边的条数.
通过观察转换后的路网, 节点度差距较大, 且有些站点间相邻交叉口较多, 距离相对较远. 故引入节点度折减系数βij, 表征站点相隔远近程度. 根据三个道路等级和三种相隔交叉口个数情况, 共9种组合方式, 综合排出优先级: 主-1>主-2>次-1>主-3>次-2>支-1>次-3>支-2>支-3,βij依次按规律从1递减, 以0.1为单位递减,βij取值见表1. 例如当道路为主干道且相隔1个交叉口时,βij取1.
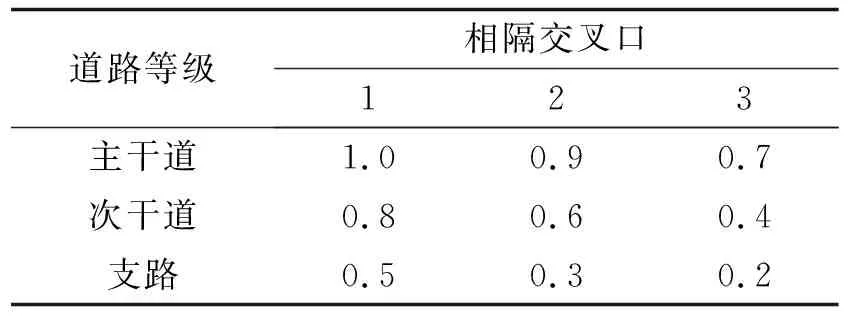
表1 节点度折减系数βij
单个节点的度按公式Ci=∑δij·βij计算, 若节点i与j能在3个交叉口内到达,δij则取1, 反之取0.
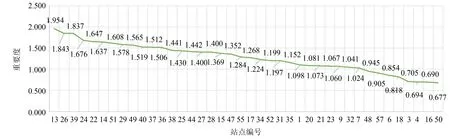
节点度指标为道路条件因素相关的静态指标, 结合动态需求, 两者权重平衡, 旨在体现交通拥堵背景下, 道路条件与乘客需求在路径寻优上同等的重要程度. 将二者归一化处理后相加, 作为站点的综合评价指标. 对站点按重要度排序, 筛选出前50%和前70%的站点作为路径寻优时考虑的停靠站点的两种方案. 归一化处理公式为:
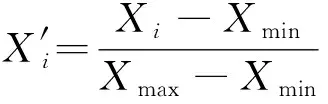
(1)
式中:Xi、X′i分别为需归一化处理前后的变量;Xmax为变量中最大值;Xmin为变量中最小值.
将节点i的节点度Ci、 站点乘客需求数Pi代入式(1), 求出归一化处理后的节点度C′i、 乘客需求数P′i, 并代入下式, 求出各站点最终重要度评估结果A.
A=C′i+P′i
(2)
2 定制公交动态路径优化模型
2.1 路径寻优目标函数
本模型从乘客需求和路网条件的角度出发, 选取两个目标: 一是服务率最大化, 二是动态行程时间最小化. 二者权重平衡, 服务率取负值, 叠加上行程时间即为综合目标函数, 当目标求解追求最小化, 此时利益最大化. 因此, 本文路径优化模型的综合目标函数为:
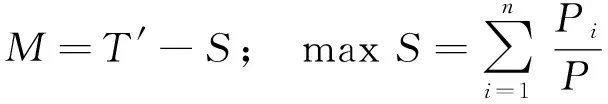
(3)
式中:S为服务率(0 从实际与建模简便性考虑, 提出以下3点假设. 1) 车辆在交叉口最多一次停车排队, 且停车排队延误d取定值; 2) 两站点i、j间经过的各个交叉口有相同的交通状态, 例如站点i、j之间相隔的交叉口的交通状态都为红灯或都为绿灯; 3) 站点间路段分为畅通、 拥挤和拥堵三个状态. 状态一: 道路畅通, 车辆较少, 定制公交可以自由流速度不停车绿灯通过交叉口; 状态二: 道路拥挤, 车辆较多, 定制公交仍可以一定速度不停车绿灯通过交叉口; 状态三: 道路拥堵, 定制公交需停车一次后通过. 每一状态图的上下部分分别表示公交车辆在路口上游与到该路口时的状态, 如图2所示. 图2 车辆通过路段状态Fig.2 Conditions of vehicle passing through road 将车辆通过i、j站点间路段a的行程时间Ta(t)分为两段之和: 非拥堵区段的行程时间ra(t)与拥堵区段的排队等待延误时间da(t), 三种状态对应的ra(t)与da(t)计算式见表2. 故行程时间: Ta(t)=ra(t)+da(t) 注: 表中La为a路段长度;vfa为自由流速度, 取设计车速;α为拥挤段速度折减系数;d为红灯排队等待延误. 因此, 整条路径的动态行程时间为T, 由于公交服务率介于0~1, 需将行程时间T作归一化处理, 标准化后的行程时间计算如下. (5) (6) 为保证定制公交线路的效益, 还需满足最大载客量、 运营成本以及行程时间3个约束条件: (7) maxQ=∑(q×dij+T×ti) (8) (9) 式中:N为最大载客量;K为公交车容量;Q为运营成本;q为每公里油耗;dij为线路里程;T为行程时间;ti为单位时间价值;B为运营成本阈值;C为行程时间阈值. 2.3.1A*算法 A*算法是在Dijkstra算法基础上改进的启发式搜索算法, 该算法通过引入估价函数, 对未搜寻节点至目标节点代价进行评估, 寻求下一最优状态节点, 加以扩展, 直到找到目标节点. 节点i的估价函数公式表示为: f(i)=g(i)+h(i) (10) 式中:f(i)是从起点经由节点i到目标节点的估计代价;g(i)是从起点到节点i的实际代价;h(i)是从节点i到目标节点的最佳路径的估计代价. 算法包含Open表和Close表, Open表记录所有已知但是尚未搜索的节点, Close记录已经历节点. 具体包括如下两步. 1) 把起点加入Open表, 检查起点相邻节点, 将可到达的节点加入到Open表, 重复下述过程. ① 遍历Open表, 查找f值最小的节点, 作为当前要处理的节点. ② 把当前节点移到Close表. ③ 对当前节点相邻节点作出判断. 如果经历3个交叉口以上才到达的节点或已在Close表中, 则忽略. 反之, 做如下操作: 如果不在Open表中, 把它加入Open表, 并把当前节点设置为父节点, 记录该节点的f、g和h值. 如果它已经在Open表中, 检查经由当前节点到达其位置的路径是否更好, 用g值作参考, 更小的g值表示更优路径. 若是, 把它的父节点设置为当前节点, 并重新计算它的g和f值. ④ 停止条件. 当把目标节点加入到Open表中, 路径搜索完毕. 2) 保存路径. 从终点开始, 每个节点沿着父节点移动直至起点, 则为待查找的路径. 2.3.2基于定制公交路径特点的改进A*算法 假设父节点为U, 相邻节点为V. 原算法中,g(V)=g(U)+cost(U,V), 即起点至当前节点的实际代价为起点至父节点实际代价与父节点至当前节点实际代价之和, 其中cost(U,V)为父节点至当前节点的代价. 综合动态行程时间与乘客需求, 调整父节点至当前节点代价cost(U,V). 调整后:g(V)=g(U)+T′-S, 考虑道路等级和交通状态两个因素的影响. 1) 动态行程时间计算中假设两站点i、j间经过的各个交叉口有相同的交通状态, 路段间若相隔2或3个交叉口且均为畅通, 即形成绿波带. 蔡雅苹等[9]通过仿真实验, 得到干线协调控制下公交车辆通过三个交叉口的平均延误仅82.9 s, 行程时间容易偏小; 若均为拥堵, 则行程时间偏大; 2) 两站点间路段有经过低等级道路按低等级道路算, 行程时间容易偏大. 为降低影响, 对动态行程加以修正, 修正后:g(V)=g(U)+ωT′-S,ω为动态行程时间的修正系数, 其余步骤不变. 以福州市部分区域为例, 起终点定为公交仁德站-火车站北广场站, 选取部分道路上共59个站点, 原始道路网络与转换后网络图(复杂程度大, 图中略去边上系数)见图3. 图3 福州市部分路网拓扑结构图Fig.3 Topological structure chart of the road network in Fuzhou 按上文建立的节点重要度评估模型对转换后的网络节点进行筛选, 除起终点外的57个站点, 重要度排序前50%(方案一)和前70%(方案二)的站点见图4, 筛选站点后的网络图见图5. 图4 站点重要度前70%筛选结果(包含前50%)Fig.4 Screening result of the top 70% stations′ importance (including the top 50%) 将筛选出的站点编号与仅按需求数排序下的站点编号进行对比, 定义站点编号重复率概念为编号相同的站点个数与对比总站点数的比值, 以此验证站点重要度评估模型. 结果表明, 方案一站点编号重复个数27个, 编号重复率为93.1%; 方案二站点编号重复个数39个, 编号重复率为97.5%. 两方案结果均在93%以上, 说明考虑道路条件因素对站点的筛选结果与仅考虑需求数的筛选结果差异较小, 且站点数越多, 筛选结果越相近. 本文建立的站点重要度评估模型有效性得以验证, 也弥补了仅考虑需求数筛选站点的不足. 图5 筛选站点后网络图Fig.5 Network chart after stations-screening 利用MATLAB2016a编程求解计算, 设定定制公交车最大载客量为40, 站点i到j与站点j到i需求相同, 主次干道和支路的自由流速度分别为50、 40、 30 km·h-1. 王吟松等[10]基于浮动车车速数据进行交通状态判别时, 得出拥挤状态的车速区间为15~30 km·h-1, 拥挤时速度折减系数α按主干道(车速按30 km·h-1计)取0.6, 次干道(车速按20 km·h-1计)和支路(车速按15 km·h-1计)取0.5. 排队等待延误时间d包含信控延误和红灯时间, 红灯取60 s, 交叉口取C级服务水平, 每车信控延误21~35 s, 取28 s, 故单个交叉口d取88 s. 动态行程时间的修正系数ω, 经过低等级道路会存在降低道路等级, 增加行程时间, 而都判为畅通的交通状态, 行程时间会低于正常值, 存在两因素可视为抵消. 对相隔2或3个交叉口的路段按照道路等级、 交通状态畅通与拥堵赋值修正系数, 主干道畅通ω=1.1, 拥堵ω=0.9, 次干道拥堵ω=0.8, 支路拥堵ω=0.7. 约束中, 油耗为2.1元·km-1, 时间平均价值为36元·h-1, 每乘客票价为6元, 运营成本阈值为200元, 行程时间阈值为60 min. 代入算法计算出方案一的最优线路目标值为0.879 22, 方案二为0.751 03, 路径响应的停靠站点编号见表3. 两种方案的乘客服务率、 上座率、 行程时间、 线路长度以及停站个数对比见表4. 表3 最优线路停靠站点 注: 表中站点编号0为起始站(公交仁德站)、 58为终点站(福州火车站). 表4 两种路径规划方案结果对比 从表4可以看出, 单辆车一条线路能服务35%左右的需求, 且对于两种站点筛选方案, 上座率都能达到92.5%以上, 线路里程在8 km左右, 两者的成本及行程时间远小于既定阈值. 方案一筛选重要度前50%的站点, 较方案二简化了路网复杂程度, 线路里程和停站个数都较方案二少, 行程时间与路径所经过的道路等级以及道路拥堵情况有关, 故出现方案一线路长度短, 但行程时间更长的结果. 以公交站点为基础, 调整原始道路交通网络的拓扑结构, 结合复杂网络理论与动态需求特征, 对动态路网中站点进行重要度评估, 筛选出重要度前50%与前70%的站点供路径停靠考虑. 结合福州市具体路网进行算例分析, 两种站点筛选方案下的动态路径只需停靠9或10个站点, 时间上仅为普通公交(36 min)的45.1%, 上座率能达到92.5%以上. 按照站点重要度前50%进行筛选得到的路径结果整体优于前70%. 此外, A*算法取决于估价函数h(i), 估价函数越准确, 即节点i到目标节点所估代价与实际代价越接近, 得到的解越接近最优解. 由于研究简化了某些交通参数, 因此在行程时间上与实际存在一定误差, 故结果为近似最优解. 本文以实际路网作为研究背景, 站点筛选能极大简化路网的复杂程度, 提高路径规划效率.

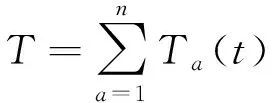
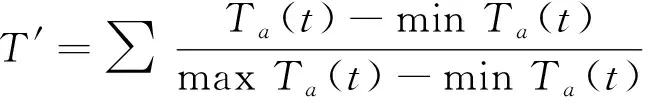
2.2 约束条件
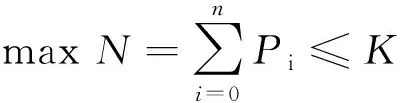
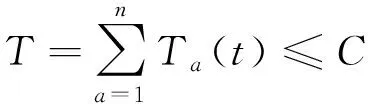
2.3 基于A*算法的动态路径求解算法
3 算例分析
3.1 定制公交停靠站点筛选
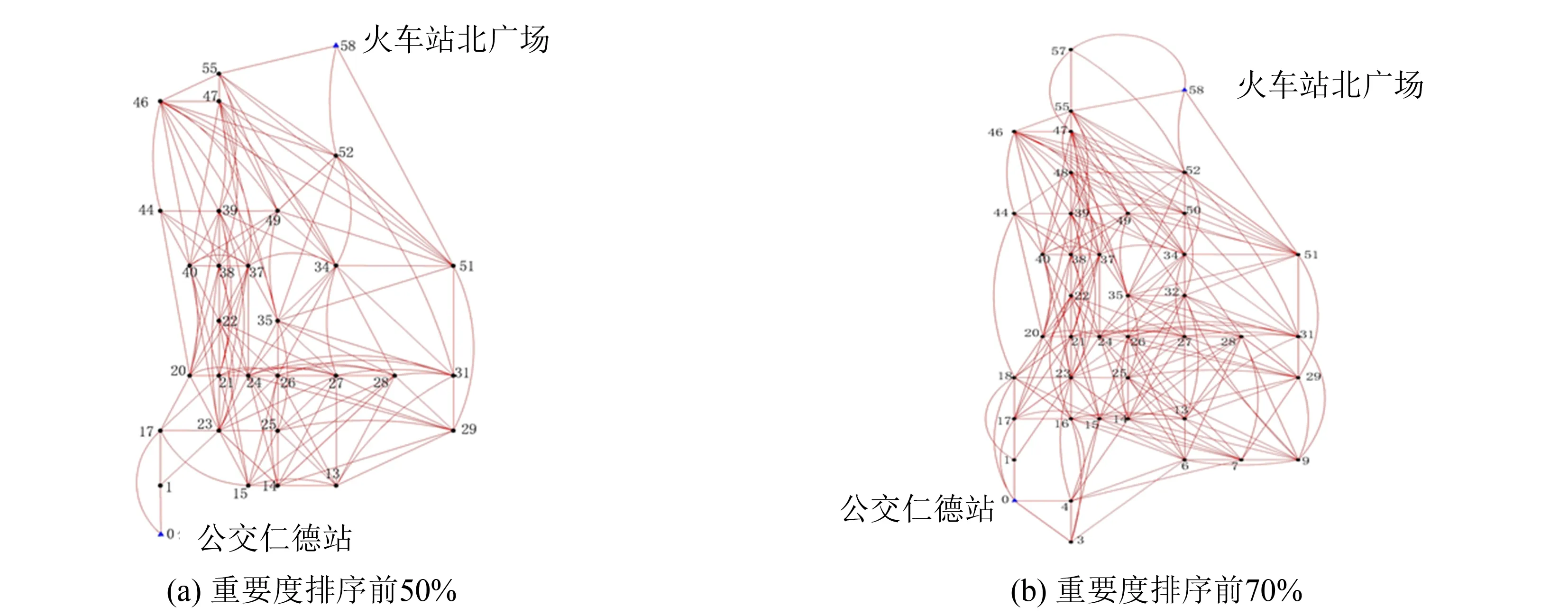
3.2 定制公交动态路径生成


4 结语

