非线性多视角子空间聚类方法

陈智平， 陈晓云， 简彩仁

(1. 福州大学数学与计算机科学学院, 福建 福州 350108; 2. 厦门大学嘉庚学院, 福建 漳州 363105)

0 引言

在多媒体应用领域, 不同视角特征组成的数据广泛存在, 如针对彩色图片, 可以由其文本、 纹理以及颜色特征表示; 同一篇文本可以由不同的语言描述. 不同视角描述了同一对象的不同方面, 具有更丰富的信息, 从而多视角学习的目的就是研究有效的多视角特征利用方法.

聚类是多视角特征分析的重要技术, 现有多视角聚类的算法主要包括: 协同训练以及子空间学习. 协同训练方法通过在不同视角上进行独立交替的训练, 从而提高学习模型的泛化能力[1-2]. 但这类方法假设不同视角特征贡献程度一样, 算法效果易受到噪声视角的影响. 子空间学习假设高维数据本质上分布在多个不同的线性子空间中, 该假设认为同类样本分布在同一个子空间, 不同类样本分布在不同的线性子空间[3-4]. 其中, 获取多视角数据的多线性子空间结构应用最广的方法是构造自表示系数矩阵, 接着用表示矩阵构建相似矩阵, 最后利用文[5]提出的谱聚类分割方法实现聚类. 对每个视角特征, 可直接利用现有的单视角学习算法进行学习, 但不同视角自表示系数矩阵不同, 因而学者们提出了不同的正则技术使得所有视角自表示系数矩阵接近或直接令其一致, 从而保证跨视角聚类一致性[6-7]. 但上述方法都是线性的, 无法处理非线性分布数据.

针对线性表示模型的不足, 提出非线性多视角子空间聚类方法(nonlinear multi-view subspace clustering, N_MVSC). N_MVSC先对数据进行非线性投影, 在新特征空间进行自表示, 并通过流形正则项从不同视角下数据的近邻关系挖掘互补信息, 对数据进行更充分的利用.

1 子空间聚类

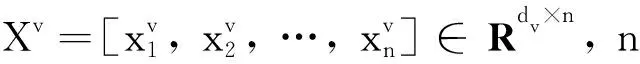
Xv=XvZv+Ev

(1)

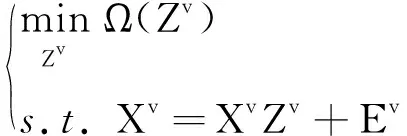
(2)

其中:Ω(Zv)是对Zv的约束, 常用的有稀疏约束[8]和低秩约束[9], 能使子空间结构表示矩阵具有更多的性质. 获得自表示矩阵Zv后, 通常相似度矩阵构造为

Sv=|Zv|+|(Zv)T|

(3)

其中: |·|表示绝对值运算, 将相似度矩阵作为谱聚类算法的输入以获得最终的聚类结果.

2 非线性多视角子空间聚类

2.1 流形正则项

文[10]指出, 距离近的样本更可能来自同一子空间. 假设样本在多个视角表示下距离都近的样本更可能来自同一子空间, 由于视角差异性的存在， 构造多视角流形正则项为

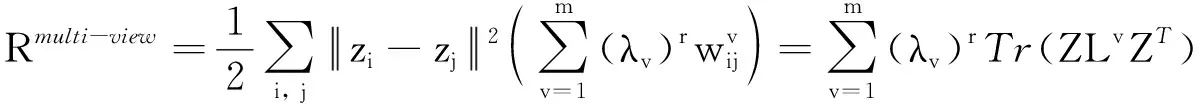
(4)

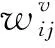
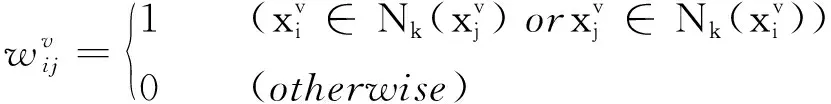
(5)

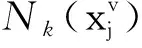
2.2 非线性投影函数

定义非线性投影函数H=[h1, h2, …, hl]T, 由l个非线性函数hi构成, 样本数据x∈Rd经过非线性投影后的表示为

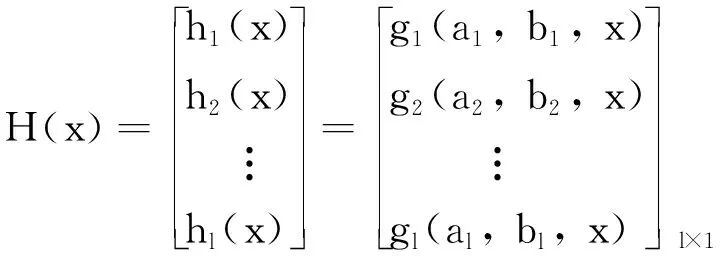
(6)

其中: 第j个非线性函数hj=gj(aj,bj, x), 参数aj∈Rd×1, bj∈R1×1为随机产生的, 其取值范围通常为[-1, 1], gj(aj, bj, x)可以是任意非线性分段连续函数, 常用的有Sigmoid函数以及Gaussian函数. 其定义为

Sigmoid函数:

Gaussian函数:

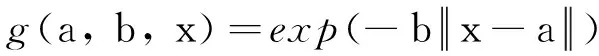
文[11]指出, 当非线性函数个数l较大时, 模型能够取得较好的泛化能力. 文[11-12]证实, 通过多个非线性函数对样本进行投影, 能够获得较好的特征表示. 原来d维的样本数据通过非线性投影后具有的维数为l维.

2.3 非线性多视角子空间聚类模型

综合流形正则项以及非线性投影, 得到本研究的目标函数:

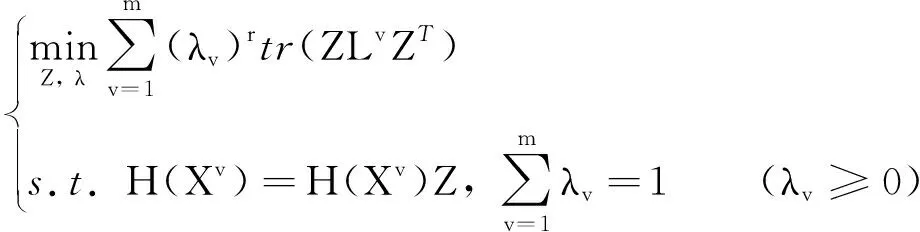
(7)

模型令所有数据在新特征空间中表示系数矩阵一致, 从而保证跨视角聚类一致性, 对于有噪声的模型, 可以扩展为

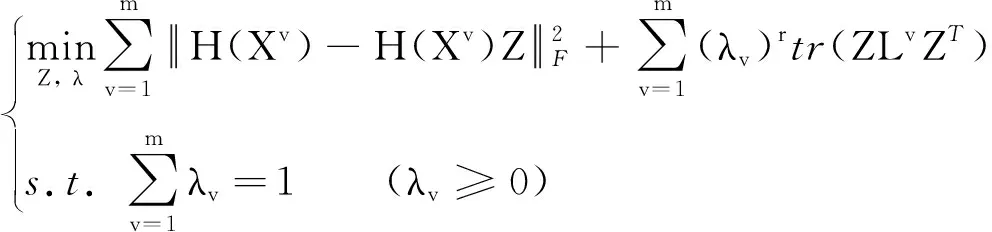
(8)

其中:λ=[λ1,λ2, …,λm]是视角权重, 其作用是避免某个视角的贡献为1, 其他视角贡献为0的情况; 模型第一项刻画容噪声性能, 第二项是多视角流形正则项, 从数据的近邻关系出发挖掘不同视角的互补信息. 此外, 模型将视角权重作为变量学习, 可以自适应为每个视角寻找最优权重[13].

2.4 模型求解

目标函数式(8)有两个变量Z, λ, 可采用交替方向迭代法[14]求解, 具体过程为

第一步, 固定λ更新Z, 令

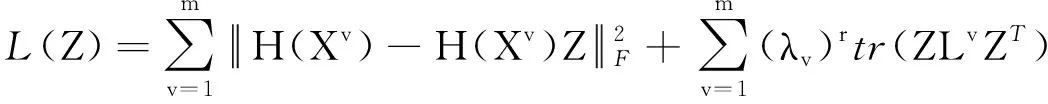
(9)

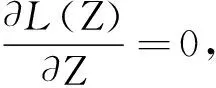
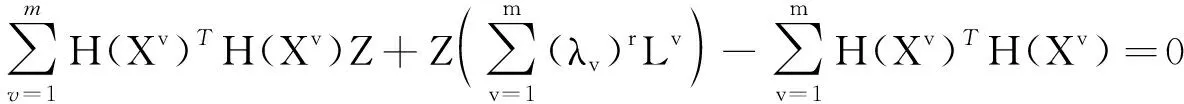
(10)

式(10)可直接通过Matlab内置函数lyap求.

第二步, 固定Z更新λ, 利用拉格朗日乘子β将等式约束带入目标函数, 得到拉格朗日函数为:

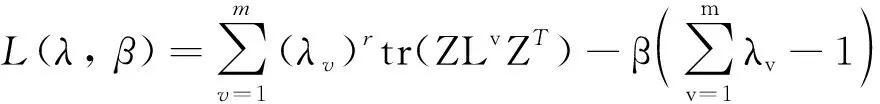
(11)

将L(λ,β)分别对λv以及β求导, 并令其结果为0, 并记hv=tr(ZLvZT), 可得:

(12)

通过简单的代数运算,λv可由下式获得:

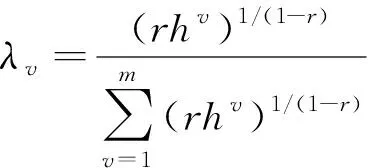
(13)

上述算法过程可总结为:

算法1: 非线性多视角子空间聚类算法(N_MVSC)输入: 多视角数据X=[X1, X2, …, Xm], 平滑参数r, 近邻数k输出: c个类簇初始化设置: 利用非线性投影函数对每个视角数据进行投影, 获得H(Xv), v=1, 2, …, m, 利用k近邻计算每个视角的邻接关系矩阵Wv, λv=1m, m为视角数, tol=10-3.循环: 1. 通过式(10)更新公共子空间表示系数矩阵Z; 2. 通过式(13)更新每个视角贡献度λv; 3. 验证是否满足收敛条件Zk+1-Zk≤tol和λk+1-λk≤tol, 若满足, 则停止循环.

3 实验分析

为验证本方法的有效性, 在三个文本数据集以及两个图像数据集上进行实验. 所有试验均使用Matlab R2015a软件编程, 试验环境为64位Windows 7操作系统, 内存4 GB， Intel(R) Core(TM) i5-4590 CPU @ 3.3.

3.1 数据集

1) 3sources. 该文本数据集来自三家在线新闻资源: BBC、 Ruters以及Guardian, 总共有948条新闻文章包含2009年2月到4月的416条地区新闻报道. 在这些报道中, 有169条新闻在三个广播电台均有报道. 每个新闻对应商业、 娱乐、 健康、 政治、 运动以及科技6个标签中的一个 . 三家不同的网站对同一则新闻的文本描述可以看做是3个不同的视角特征.

2) 20newsgroups. 该文本数据集包含约20 000个新闻组文档, 根据主题可划分为20个不同的新闻组. 同文[15]构造方式, 提取2 000个词构造子集, 选择comp.graphics、 rec.motorcycles、 rec.sport.baseball、 sci.space, talk以及politics.mideast 5个类别. 对文本数据采用忽略文件头、 将大写字符改成小写以及忽略包含数字或非字母数字字符的所有单词3种不同的预处理方式, 可视为3个不同的视角特征.

3) MSRC. 该图像数据集包含240张图像, 8个类别. 同文[16], 选择树、 建筑、 飞机、 奶牛、 脸、 汽车、 自行车7个类别, 从每张图像提取24维颜色矩、 512维GIST、 256维局部二值特征以及254维Centrist特征4个视觉特征, 不同的视觉特征可看做不同的视角, 视角数为4.

4) BBCSport. 该新闻数据集包含737条BBC体育网站在2004—2005年5个运动主题新闻, 例如竞技、 板球、 足球、 橄榄球和网球. 使用该数据集的一个子集, 由文 [15]作者提供. 该人造数据集的视角由文档分割方式产生, 本实验选择其中两种分割方式: 对同一个文档分割成两个段落最后合并成一个段落以及对同一个文档分割成2个段落最后保留两个段落.

5) Gait3. CASIA B[17]是公开的多视角数据集, 包含124个人来自11个不同角度(0°, 18°, …, 180°)的监控摄像, 每个人有10张步态图片: 6张正常行走、 2张穿大衣行走及2张带包行走. 本实验选择前三个视角度下120个人正常行走的步态样本, 则样本数为720， 视角数为3.

3.2 对比方法

将本方法(N_MVSC)分别与Co-train[1]、 Co-reg[2]、 SC[5]、 AMGL[16]、 MLAN[18]、 L_MVSC进行对比. 其中Co-train与Co-reg是基于协同训练的方法; SC将所有视角特征串联成单个视角特征作为谱聚类算法的输入, 用以说明简单的视角特征串联方法的可行性; L_MVSC是N_MVSC不进行非线性投影的模型, 用以对比非线性投影函数的作用; AMGL以及MLAN是近年提出的性能较好的方法.

对比方法中, 原文献没有给出参数遍历范围的, 其参数均在[10-3, 10-2, …, 103]中遍历寻优, Co-reg的正则参数范围为[0.01, 0.02, …, 0.05], 间隔为0.01. 对本研究所提方法N_MVSC以及对应的线性方法L_MVSC设定相关条件: 平滑参数r的搜索范围均为[0.1, 0.3, …, 1.1], 间隔为0.2, 采用Sigmoid构造非线性投影函数, 非线性函数个数取l=1 000; 采用7近邻构造每个视角的拉普拉斯矩阵: 对本研究所有对比实验中先学习相似矩阵, 再使用谱聚类算法进行分割的模型, 均使用文[5]的谱聚类分割模型将数据分成c个空间. 由于谱聚类分割中k-means随机初始中心选取, 以及多非线性投影过程中随机权重产生的影响, 实验中在固定平滑参数r的情况下, 让N_MVSC分别运行10次, 再对每次学习的子空间表示系数进行10次谱聚类分割, 取100次聚类准确率的均值作为最终准确率. 其余对比方法均取10次聚类准确率均值为最终准确率.

3.3 实验结果分析

采用聚类准确率(ACC)和规范化互信息(NMI)作为评价指标, 其值越高, 代表聚类效果越好, 结果表1， 表2所示.

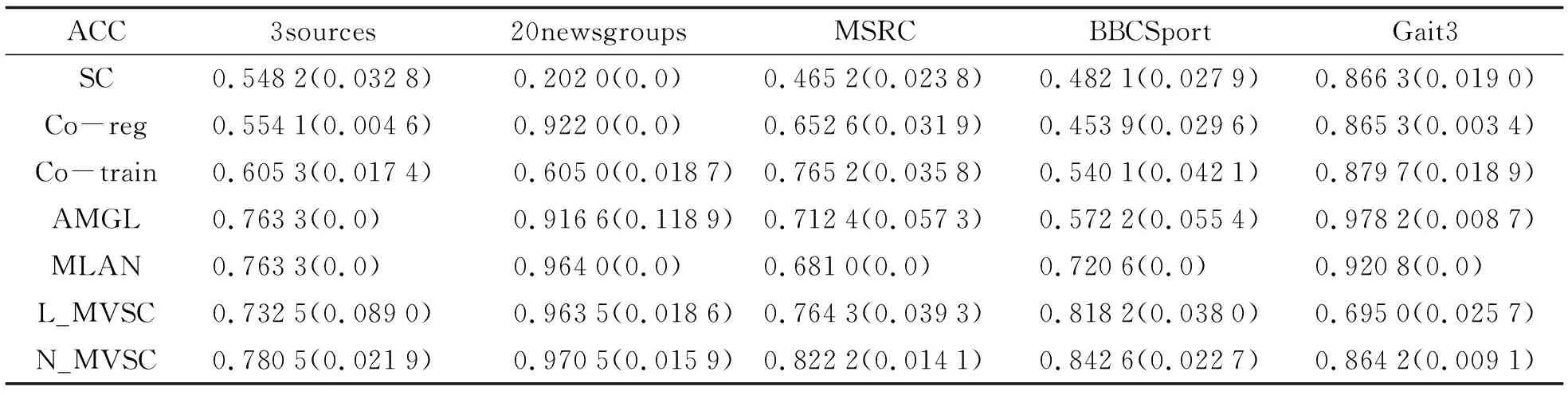
表1 五个数据集上聚类准确率对比

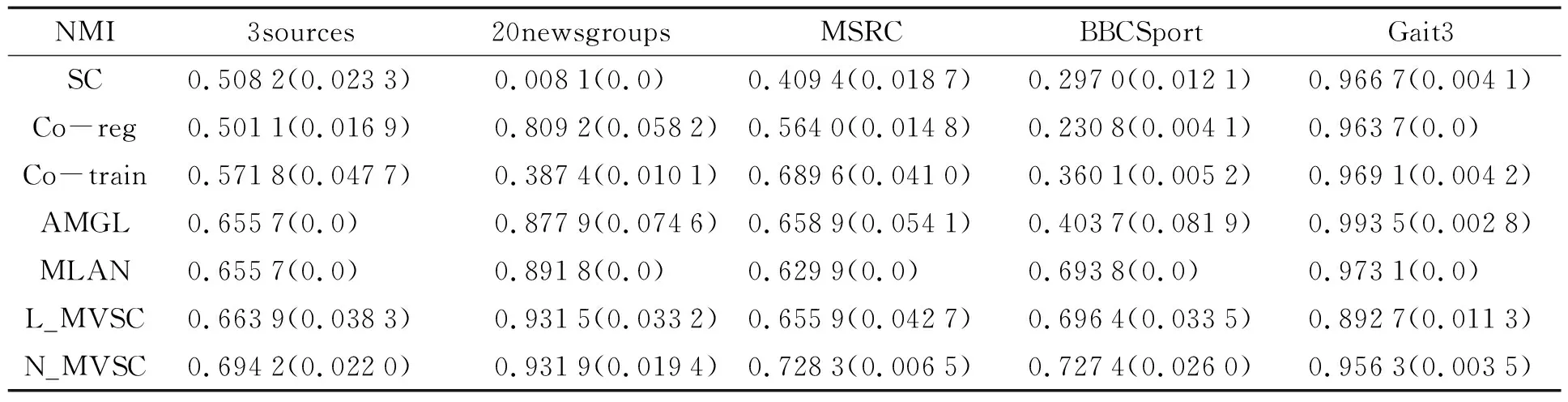
表2 五个数据集上的规范化互信息对比

通过上述实验， 可以发现:

1) N_MVSC在所有数据集上的实验结果均优于L_MVSC, 说明N_MVSC通过对数据进行非线性投影, 能够更好刻画多视角数据的非线性性质.

2) 对比其他方法, N_MVSC在除Gait3外的其余四个数据集上均取得最佳聚类效果. 究其原因在于N_MVSC不仅通过非线性投影刻画数据间的非线性表示关系, 并且通过k近邻构造流形正则项, 从数据的局部几何关系发现不同视角的相似模式. 对比方法Co-reg、 Co-train、 AMGL通过给定的距离度量计算所有样本之间的相似度, 不利于刻画数据的流形结构, 因而效果不理想； N_MVSC在数据集Gait3上的实验结果不是很理想, 一个可能的原因是步态数据集中于同一个人， 不仅有不同角度拍摄下的表示, 还有不同携带条件(穿大衣、 背包等)上的差异, 造成不同视角数据分布上差异较大, 从而所在子空间的差异较大, 造成N_MVSC效果不理想.

3) SC在除Gait3数据集外的其余四个数据集上的聚类效果均不理想, 在20newsgroups上均取得最差实验结果, 说明直接将所有视角数据拼接成单个视角数据是不合理的多视角数据处理方法, 该方法忽略了不同视角数据本身的统计特性.

为进一步说明多视角学习的优越性, 将本方法N_MVSC应用在多视角数据集MSRC上, 对比输入不同视角数时算法的聚类性能, 结果如表3所示.

从表3可知, 随着视角数的增加, N_MVSC的聚类准确率不断提高, 说明多视角特征对比单视角具有更多的信息, 对这些特征进行有效利用能够提高单视角聚类任务的效果. 这从另一个方面说明本方法是有效的多视角聚类算法.

表3 N_MVSC在不同视角数下的聚类性能

3.4 非线性投影性能分析

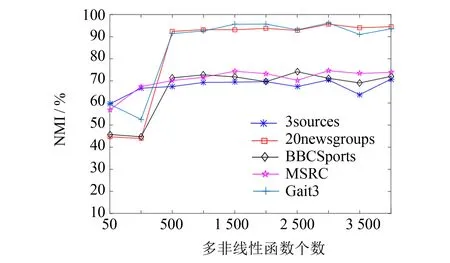
图1 多非线性投影函数个数对实验结果的影响 Fig.1 Influence of the number of multi-nonlinear projection functions on the experimental results

为分析非线性投影中不同的非线性函数个数l对实验结果的影响, 在NMI评价指标下, 分别取l为50、 100、 500、 1 000、 1 500、 2 000、 2 500、 3 000、 3 500、 4 000下的聚类效果进行比较, 在五个数据集上的结果如图1所示.

由图1可知, 当l取值在500以上时, 非线性投影函数受随机权重赋值影响减小, 算法N_MVSC结果稳定； 对数据集Gait3、 20newsgroups以及BBCSport, 随着非线性函数个数的增加, 其提升效果明显.

3.5 参数分析

在构造多视角图正则项时, 存在两个参数, 一个是平滑参数r, 一个是近邻数k, 其中r的作用是平滑不同视角的贡献, 近邻数k刻画不同的流形结构. 由于非线性投影函数个数l取值在500以上时, 投影效果稳定, 因而本节进行参数分析时, 固定l=1 000,r的取值范围为{0.1, 0.3, 0.5, 0.7, 0.9, 1.1}, 参数k的取值范围为{1, 2, 3, 5, 7, 9, 12}, 取ACC评价指标下的聚类效果, 聚类准确率如图2所示.

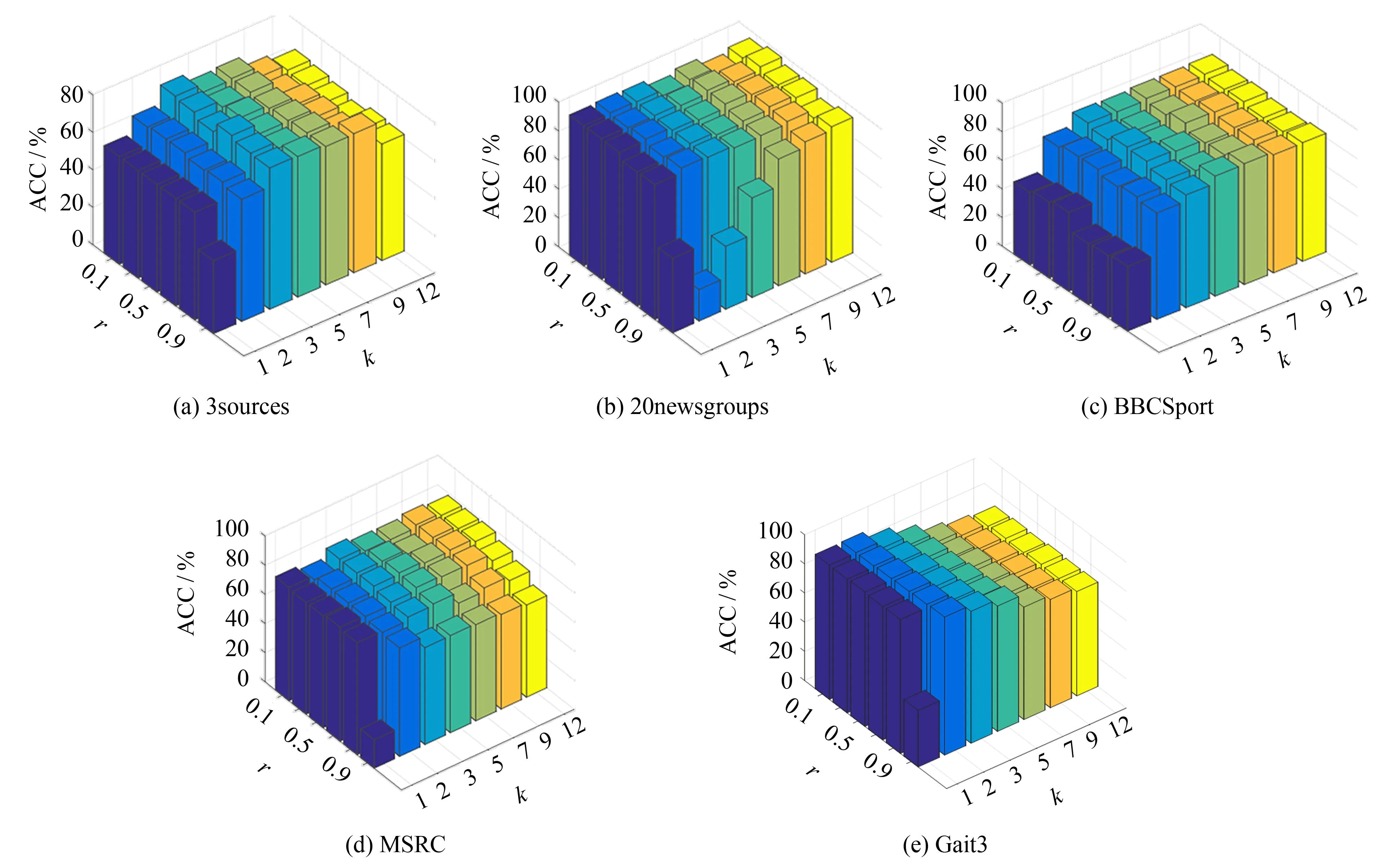
图2 不同k和r取值下的聚类准确率Fig.2 Clustering accuracy under different k and r

由图2可见, 当近邻数k取值为5, 7, 9, 12, 平滑参数取值在1.1以下时, N_MVSC的大部分数据能够获得较好的聚类准确率;k取值较小时, 效果较差, 说明近邻数太小难以保持原始数据的低维流形结构; 在固定k的情况下(如k=7), N_MVSC在不同数据集上随r的变化趋势不同, 这是由于不同的多视角数据的差异性, 造成了r在平滑视角贡献上的差异.

4 结语

提出一种非线性多视角子空间聚类方法, 从数据间的非线性表示关系以及数据的流形结构两方面考虑数据的非线性性质, 并将其成功应用于多视角聚类研究中. N_MVSC在大部分数据集上聚类效果优于现有方法, 说明同时结合两种非线性技术能够保留数据更多的信息, 从而具有更好的效果.