基于紫外光谱的水体硝酸盐氮浊度补偿研究
陈 颖, 何 磊, 崔行宁, 肖春艳, 张 杰, 张 灿, 杨 惠, 周鑫德, 李少华
1. 燕山大学电气工程学院河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004 2. 河南理工大学资源与环境学院, 河南 焦作 454000 3. 河北先河环保科技股份有限公司, 河北 石家庄 050000
引 言
硝酸盐氮是含氮有机物氧化分解的最终产物, 是一项重要的水质污染指标, 如果含量过高则会造成水质富营养化, 导致生态失衡, 饮用水中含量过高会对人体健康造成很大威胁, 因此对此污染物检测尤为重要[1-2]。 浊度可以反映溶液对光通过溶液时所产生的阻碍程度, 它包括溶液中悬浮物对光的反射以及溶质分子对光的吸收。 浊度不仅与悬浮物的含量相关, 还和其形状、 大小、 折射系数息息相关[3-5]。 在紫外光谱法的硝酸盐氮检测中, 由于水体中悬浮物的散射作用, 会使吸收光谱发生很大变化, 对测量的建模数据产生较大的误差, 造成反演浓度的不准确, 因此, 有必要消除浊度的影响。
在浊度补偿方面, 研究学者做了很多工作, 梁康甫等[6]在分光光度法测量水中总磷时, 提出了一种双波长法来减小浊度的干扰, 用待测溶液490 nm波长处的吸光度来补偿700 nm波长处的吸光度, 浊度补偿效果较好。 宋建军等[7]利用多波长紫外吸收光谱法与偏最小二乘回归相结合算法预测水样中的化学需氧量, 同时考虑了浊度对建模所用的吸光度的影响, 使用线性方程对浊度的影响进行了补偿。 吴德操等[8]采用基于Mie散射理论的光全散射颗粒物粒径分析重建了水样本所含颗粒物的粒径分布, 利用粒径分布的二次反演, 估计了220~450 nm可溶有机物特征光谱段中由颗粒物引起的消光值, 实现了对浊度干扰的精确补偿。
常规的紫外吸收光谱消除浊度的影响一般通过单波长补偿法, 利用350 nm的吸光度作为浊度补偿[9], 即在吸收峰处的吸光度减去350 nm的吸光度, 再对补偿后的吸收峰建立线性回归预测模型, 但是此方法容易受到干扰, 并且浊度会对很长的波段产生影响, 造成预测模型的不准确。
针对水体环境中不同浊度对硝酸盐氮吸收光谱的变化情况, 在实验室条件下, 通过实验分析了不同浓度的福尔马肼浊度液对硝酸盐氮标准液的紫外吸收光谱的影响。 基于此提出了一种新的浊度补偿方法, 即在硝酸盐氮的主要吸收光谱范围内分别求出不同浊度在不同波长处的补偿系数, 从而形成不同浊度对应的补偿曲线, 利用补偿曲线对浊度进行补偿和硝酸盐氮光谱的校正。 光谱校正完成后, 建立硝酸盐氮的回归预测模型, 反演硝酸盐氮的浓度。
1 实验部分
1.1 装置
为了采集硝酸盐氮、 浊度以及两者混合溶液的紫外吸收光谱, 在实验室条件下搭建了光谱采集测试系统。 采集系统主要由光源、 耦合光纤、 脉冲调节器、 光谱仪、 样品槽构成。 光源采用集成的氙灯光源(HPX-2000), 光谱范围190~2 200 nm, 并自带有高效率耦合SMA905光纤接口输出; 光谱仪为日本YOKOGAWA光谱仪(AQ6370D-10), 灵敏度高, 分辨率高; 比色皿为美国Ocean Optics公司的高通透石英比色皿; 脉冲调节器通过同步脉冲调节光谱仪与光源, 避免产生光路延迟, 对测量结果产生误差。 测量的光谱数据通过数据线传输到电脑中进行数据处理与建模。
1.2 硝酸盐氮与浊度吸收光谱
一般水体的硝酸盐氮浓度为0.2~5 mg·L-1, 通过硝酸盐氮标准样品(1 000 mg·L-1)稀释配制了0.2~10 mg·L-1的12组样本, 光谱采集范围200~400 nm, 步长为1 nm, 每一组样本重复测量3次, 吸光度数据取平均值, 对测量的光谱数据进行简单的数据预处理。 硝酸盐氮紫外吸收光谱如图1所示, 可以看出硝酸盐氮的主要吸收谱区在200~240 nm, 这是因为硝酸根离子官能团主要在此波段有吸收。 当波长大于240 nm时, 吸光度基本为0, 因此建立硝酸盐氮预测模型时, 选择此波段光谱数据建模即可。
通过400 NTU的浊度标准液(福尔马肼溶液)与去离子水配制不同浊度的样本, 配制前先将浊度标准液充分摇匀, 在室温下完成标准液稀释, 稀释的公式为
(1)
其中,M为浊度标准液的量(mL);N为需要配制的样本溶液的浊度(NTU);K为浊度标准液的浊度(NTU),V为样本溶液的总配制量(mL)。 按照浊度梯度为5 NTU分别配制了5~50 NTU的10组浊度样本。 通过实验室的紫外吸收光谱采集系统采集不同浊度溶液的紫外吸收光谱, 如图2所示, 光谱范围为200~400 nm, 步长为1 nm。 可以发现, 在紫外光谱的范围内, 浊度溶液只有一个吸收峰, 吸收峰在217 nm左右。 波峰的左边变化较迅速, 出现了部分的光谱重叠, 右边的光谱变化较为平缓, 在整个紫外波段, 浊度溶液都有吸收。

图1 硝酸盐氮紫外吸收光谱

图2 不同浊度标准液吸收光谱
1.3 混合溶液吸收光谱
为了验证浊度对硝酸盐氮紫外吸收谱的影响, 分别配置了硝酸盐氮浓度均为2 mg·L-1, 而不同浊度(5, 10, 15, 20, 25, 30, 35, 40, 45和50 NTU)的混合溶液。
混合溶液的紫外吸收光谱如图3所示, 分析可知, 浊度对硝酸盐氮吸收谱的影响很大, 通过对比图2与图3, 混合溶液在硝酸盐氮的主要光谱吸收区(210~240 nm)的吸光度值并不是硝酸盐氮与浊度吸光度的简单叠加。 这是因为在混合溶液中, 由于浊度颗粒打破了硝酸盐氮分子的共面性, 造成空间位阻, 使共轭体系被破坏, 导致硝酸盐氮吸光度降低[10]。
硝酸盐氮吸收峰处的混合溶液吸光度与两种溶质吸光度之和的差值如图4所示, 其中竖直直线上端的值为浊度与2 mg·L-1硝酸盐氮的吸光度之和, 下端为混合溶液的吸光度值, 竖直直线的长度即为两者的差值。 分析可得, 随着浊度值的增加, 竖直直线长度变长, 两者的差值越来越大, 浊度对硝酸盐氮的吸收峰影响越来越大。 浊度浓度的升高导致硝酸盐氮的共轭体系破坏的更加严重, 因此进行浊度补偿很重要。

图3 混合溶液吸收光谱

图4 混合溶液与溶质吸光度之和差值
2 浊度补偿
本文提出了一种新的浊度补偿方法, 具体流程图如图5所示。 首先采集硝氮与浊度混合溶液的吸收光谱, 建立浊度的解算模型求出混合溶液的浊度值。 得到浊度值之后, 利用不同浊度的补偿曲线进行浊度补偿。 补偿完成后, 将光谱数据带入到建立的硝酸盐氮预测模型中即可反演出混合溶液中硝酸盐氮的浓度。

图5 浊度补偿流程
2.1 浊度解算模型
由图2可以得出, 不同浊度溶液的吸收光谱变化基本一致, 因此可以对光谱进行归一化处理, 将吸光度的值转化为0到1的无量纲值, 便于进行分析, 公式为
(2)
其中,A′(λ)为归一化之后波长λ处的吸光度,Amax和Amin分别为波长范围内的浊度的最大吸光度与最小吸光度。 归一化之后的浊度吸收光谱如图6所示。 根据归一化公式可知, 如果归一化光谱重叠, 则说明不同浊度溶液在该波段的吸收光谱变化趋势一致, 且相同波长处的吸光度线性变化, 因此适合建立线性回归模型[11]。

图6 不同浊度0-1归一化光谱
分析图6可知, 不同浊度的归一化光谱在350~400 nm波段基本重合, 因此该波段用来建立浊度的回归方程最佳。 选择此波段一方面可以消除单波长回归建模易受干扰的特点, 增加回归模型的稳定性, 另外, 通过前面的分析, 此波段(350~400 nm)的硝酸盐氮吸光度基本为0, 混合溶液吸光度只与浊度相关, 且两者的吸光度基本相同。 因此, 可以在此波段建立模型, 解算出混合溶液的浊度值, 然后进行浊度补偿。

图7 浊度解算回归模型
对此波段进行光谱积分, 即求出350~400 nm的光谱面积, 建立光谱面积与浊度值的回归模型。 如图7所示, 回归方程为y=0.269 2x+0.064 1, 相关系数R的平方为0.998 5, 可以得出此浊度解算模型效果很好。
2.2 浊度补偿原理
理论上, 根据朗伯-比尔定律, 当溶液中含有多种溶质时, 每个波长下的吸光度等于各个溶质吸光度相加的和, 如式(3)和式(4)所示
I=I0e-kNO3-NcLe-kturTL
(3)
A(λ)=ANO3-N(λ)+Atur(λ)
(4)
其中,kNO3-N和ktur分别为硝酸盐氮、 浊度溶液的吸光系数,c为硝酸盐氮的浓度值,T为浊度值,L为测量光程,A(λ),ANO3-N(λ)和Atur(λ)分别为波长λ下的混合溶液、 硝酸盐氮溶液、 浊度溶液的吸光度。
经过实验分析, 式(4)中的表达式会发生偏差, 为了描述浊度对硝酸盐氮吸光度的影响, 引入了一个在0到1之间的补偿系数kN(λ)
A(λ)=kN(λ)ANO3-N(λ)+Atur(λ)
(5)
它的值与波长有关, 当kN(λ)的值越接近0, 则说明此波长下浊度对硝酸盐氮吸光度的影响越大。
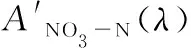

图8 (a)不同浊度下的硝酸盐氮补偿曲线;
Fig.8 (a) Nitrate and nitrogen compensation curves under different turbidity; (b) Compensation coefficient of Valley of different compensation curves
(6)
2.3 验证结果分析
通过前面求出的浊度补偿模型对混合溶液进行浊度补偿, 补偿完成后即可得到校正之后的光谱。 通过前面的12组硝酸盐氮吸收光谱建立了偏最小二乘算法(PLS)的预测模型。 校正后的光谱代入预测模型中即可反演出混合溶液中硝酸盐氮的浓度。 浊度曲线补偿后硝酸盐氮预测结果如图9所示, 并与未进行浊度补偿时、 单波长补偿法预测结果进行了对比。

图9 不同补偿方法预测结果图
分析可知, 当没有进行浊度补偿时, 硝酸盐氮浓度预测值会发生很大偏移, 预测结果误差很大, 并且随着混合溶液浊度的升高, 硝酸盐氮浓度的预测结果误差越来越大。 单波长的补偿方法也是随着浊度的升高发生较大偏移。 基于补偿曲线进行浊度补偿后, 预测值在真实值上下浮动, 补偿效果明显优于单波长的补偿方法。 由表1可知, 预测值与真实值的平均绝对误差为5.3%, RMSEP为0.124, 预测精度较高, 说明基于补偿曲线的浊度补偿方法是可行的。

表1 补偿曲线法PLS模型预测结果
3 结 论
通过实验方法分析了福尔马肼浊度标准液对硝酸盐氮标准液紫外吸收光谱的影响, 基于此引入补偿系数kN(λ)来表征浊度对硝酸盐氮吸收谱的影响。 根据实验测量的光谱数据求出不同浊度下硝酸盐氮主要吸收谱区的补偿系数, 即可得到其补偿曲线。 建立了基于350~400 nm光谱积分的浊度回归模型用来解算混合溶液的浊度值, 该回归模型的相关系数R的平方为0.998 5, 浊度解算模型效果较好, 得到浊度值之后即可进行浊度补偿。 通过实验对该补偿方法进行了验证, 验证结果表明, 补偿曲线法进行浊度补偿后, 建立PLS的硝酸盐氮预测模型, 预测值与真实值的平均绝对误差为5.3%, RMSEP为0.124, 误差较小。 并与单波长的浊度补偿与未进行补偿进行了对比, 相比之下, 本文提出的补偿方法效果明显优于其他两种, 此方法可以为硝酸盐氮紫外吸收光谱的浊度补偿提供有效的技术参考。

