基于时频熵和神经网络的光伏发电功率预测模型

孙志强，李东阳

(中南大学能源科学与工程学院，湖南长沙，410083)

光伏电站发电功率与发电量受太阳辐射强度、温度等不稳定因素的影响会发生波动，且波动程度较大，随机性强，并入电网后容易造成电网电压不稳定、谐波含量增加、调度管理不便等问题[1-3]，为此，电网采取拉闸限电等措施避免光伏电站对电网安全和稳定造成的影响，但这不利于清洁能源的发展，也会使光伏电站损失收益，因此，有必要对光伏电站发电功率进行准确预测，以便为电网合理调度及时消峰填谷，保证电网平滑功率输出。目前，国内外研究人员提出许多对光伏电站发电功率进行预测的方法，如：冉成科等[4]提出一种基于日类型融合理论的BP 神经网络预测光伏发电功率的方法，求出影响光伏发电的主要5个因素与发电功率相关系数，融合成1个影响因子作为BP 网络输入；耿博等[5]结合相似日理论与GA-BP 神经网络进行光功率预测；NORDIN等[6]使用神经网络，采用不同输入分别进行预测，找出了与发电功率相关系数最高的影响因素；LORENZ等[7]提出一种改进的欧洲中尺度天气预报中心太阳辐射预测模型，但需依赖准确的天气预报信息；代倩等[8]将气温、湿度等组合表征太阳辐照度，对无太阳辐照度的短期光伏发电功率进行预测，但预测精度不高；茆美琴等[9]提出一种EEMD-SVM 光伏短期出力预测的模型并将天气分为突变天气与非突变天气共2种类型，预测整点时刻的光伏发电功率；姚仲敏等[10]分别采用BP、遗传算法和粒子群算法优化的BP神经网络算法构建出晴天、雨天和多天这3种天气条件下的短期光伏发电功率预测模型；于群等[11]将光伏发电功率历史数据进行集合经验模态分解(ensemble empirical mode decomposition，EEMD)，各分量重构后作为BP 神经网络的输入，提高了预测精度，但气象因素只考虑了气温且重构后的分量，没有进一步分类处理发挥出其便捷性。本文提出一种基于时频熵和神经网络的光伏发电功率预测方法，选用BP神经网络作为预测工具，与时频熵、EEMD 处理的发电功率历史数据和气象参数一起构建预测模型。先将光伏电站发电功率历史数据按晴天、雨天和多云天分类，由EEMD 分解后由游程检测法重构成含有超短期发电功率规律的高频分量和含有短期发电功率规律的中频分量，分别经Hilbert变换得到各数据点的频率与幅值，进而在时频域中构建能量谱图，提取3种天气条件下的高频、中频分量对应的时频熵，与气象数据辐射强度、温度、相对湿度和风速及由EEMD 解得到的高频或中频分量一起作为BP神经网络的输入，分别进行光伏发电功率超短期和短期预测，且由实例验证此方法的有效性。

1 光伏发电功率影响因素

1.1 不同天气类型对光伏发电功率的影响

分析光伏发电功率的影响因素对有效进行光功率预测及提高预测精度有重要意义。光伏电站发电功率受多种因素的影响，不同天气条件下发电量不同，每个时刻发电功率也会发生变化。图1所示为某13 MW 光伏电站在同一季度、不同天气条件下的发电功率，时间从6:30 至17:30。从图1可看出：晴天发电功率随太阳辐射强度的增大或减小而稳定变化；雨天发电量最小，多云天气发电功率波动最大；不同天气的发电功率曲线区别较大，但在相同天气条件下发电功率曲线相似，周期性变化规律相近。据此将发电功率历史数据按晴天、雨天、多云天气分类后分别对光功率进行预测。

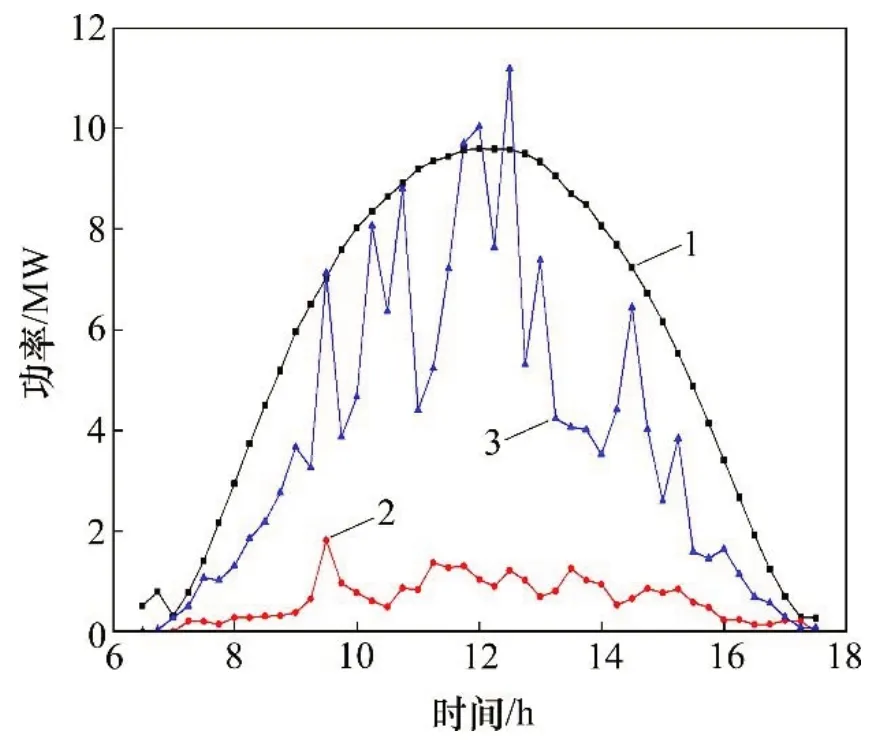
图1 不同天气类型的光伏发电功率Fig.1 Photovoltaic power generation for different weather types

1.2 气象因素对光伏发电功率的影响

光伏发电功率的工程计算式为[12]

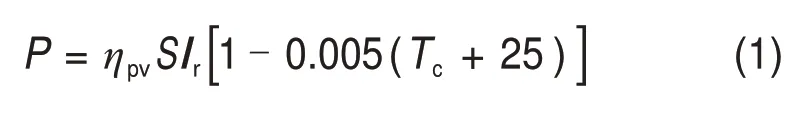
式中：ηpv为光伏效率；S为光伏电池板总面积；Ir为太阳辐射强度；Tc为光伏电池板温度。进行短期或超短期光功率预测时，光伏系统发电功率除了与上述因素有关外，还与风速、相对湿度、环境温度及电池板安装角度等有关[4]，但对于特定电站，电池板安装角度、光伏系统效率及总面积等电站自身因素是确定的，且对光功率预测的影响已经隐含在历史发电功率中，因此，进行短期或超短期光功率预测时，只需考虑温度、辐射强度、风速、相对湿度这几个对光伏发电功率预测影响较大的气象因素。光伏发电功率短期预测一般指1～2 d 内的功率预测，本文指1 d 内的功率预测；超短期预测一般指0～4 h 内的功率预测，文中指2 h的功率预测。

2 EEMD-Hilbert法提取时频熵

2.1 EEMD数据处理

经验模态分解(empirical mode decomposition，EMD)信号处理方法是根据信号局部特征，自适应地将复杂的非线性信号按频率层次逐级分解，形成一系列内禀模态分量(intrinsic mode function，IMF)[13]。EMD 具有自适应性、近似正交性及完备性，但当信号极值点分布不均匀时，易出现模态混淆现象[14]，为此，WU等[15]提出EMD的改善方法EEMD，即在信号中加入频率均匀分布的白噪声，对信号进行多次分解、集总平均后，由于噪声的零均值特性，噪声将相互抵消，集总均值即为EEMD的结果。EEMD具体步骤如下[16]。

1) 在原始信号x（t）中加入服从正态分布的白噪声ei（t），加噪后信号为

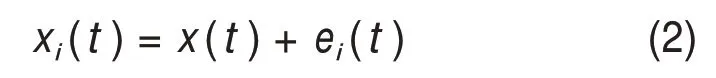
式中：ei(t)为第i次加的白噪声。

2)用EMD 方法对加噪信号xi(t)进行分解，得到n个IMF分量cj(t)和1个剩余分量r0(t)：

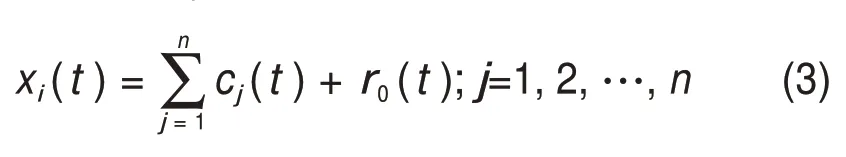
式中：cj(t)为EEMD分解得到的第j个IMF分量。

3)再次加入新的白噪声，重复步骤2)。

4)对所得IMF 分量进行集总平均，则原信号的IMF分量ci（t）为

四是定责任。党支部开展主题党日前3天将活动方案（包括时间地点、活动主题、参加人员等）报上级党组织备案，提前1天通知到所有党员，提高党员参与率和积极性。活动后及时将活动情况报上级党组织，并对活动开展情况及活动照片全程留痕纪实管理，作为基层党建考核述职评议的重要内容。把党员参加主题党日活动情况纳入党员积分制管理，作为党员民主评议、处置不合格党员和党员评先评优的重要依据。

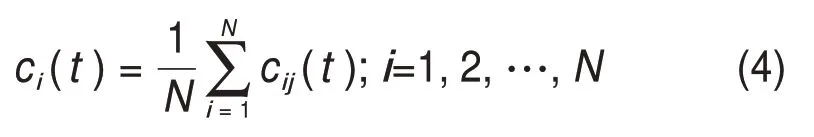
式中：N为加入白噪声的次数。

5)原始信号x(t)分解为

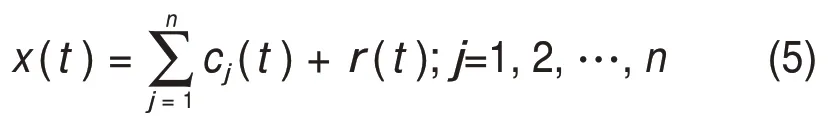
用EEMD 方法按以上步骤分别处理晴天、雨天、多云天气条件下的电站发电功率历史值，得到一系列频率由高到低的9个IMF分量，用游程检验法将IMF分量重构成高、中、低频共3组分量。

游程检验法常用于检验样本的随机性，而在文中用于检验由EEMD 分解光伏电站发电功率历史数据得到的各项IMF 分量游程个数和最大游程长度，将其作为IMF 分量重构的依据。假设每个IMF分量对应的时间序列为{T(t)}(t=1，2，…，n)，平均值为Ta，则时序符号定义为

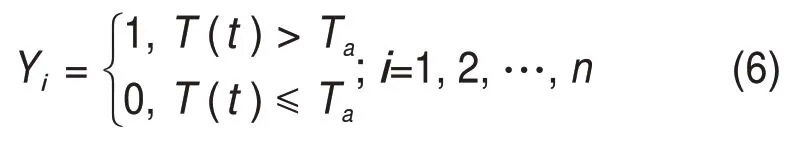
Yi是由0和1组成的总个数为n的数字串，连续的一段0 或1 都记为1 个游程，1 个游程内0 或1 的个数为游程长度，结合游程个数及最大游程长度可以检测出数据波动程度，游程个数越大，则最大游程长度越小，表示数据波动越强，频率越高。将游程数大于阈值的IMF 分量合并成1 个高频分量，显示出光伏发电功率的超短期规律；将游程数低于阈值但体现出短期周期性的IMF 分量合并成1个中频分量，能呈现出光伏发电功率的短期规律；剩下的几个游程数更小且周期很大，即最大游程长度很长的分量对数据波动影响不大，合并为光伏发电功率的低频分量，是光伏发电功率长期趋势项，而长期预测准确度太低且对电站意义不大，本文暂不考虑。表1所示为以晴天的发电功率历史数据为例，分别列出EEMD 分解后的9 个IMF分量的游程数及最大游程长度，依据游程检测法将其中c1和c2合并为高频分量，c3，c4和c5合并为中频分量。

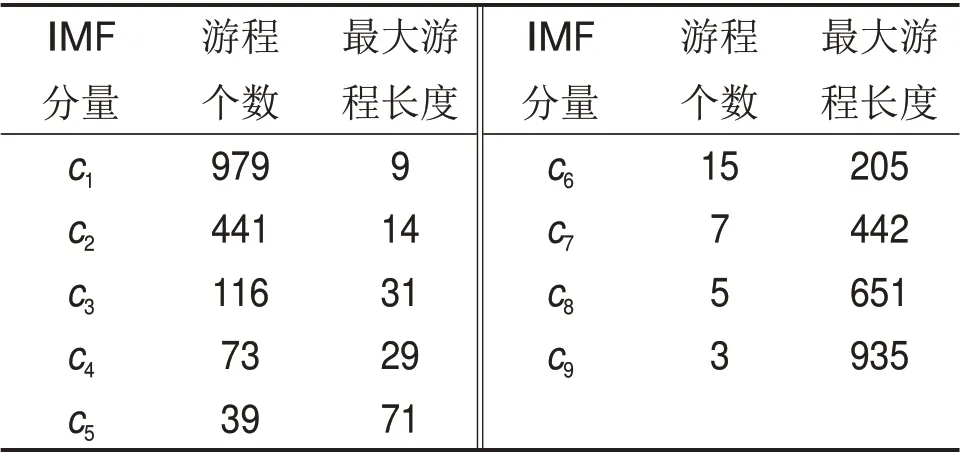
表1 游程数及最大游程长度Table 1 Number of runs and the maximum run length

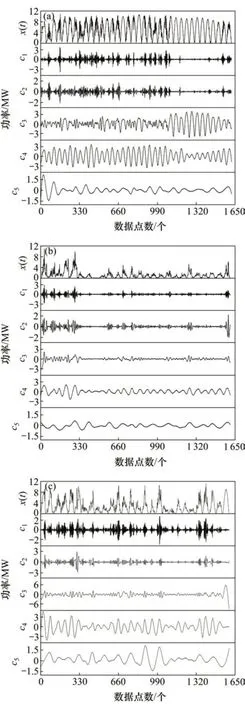
图2 不同天气的光伏发电功率历史数据EEMD分量Fig.2 EEMD components of photoelectric power historical values in different weathers

图2所示为晴天、雨天和多云天的光伏发电功率历史数据经EEMD 分解后根据游程检测法取的前5个IMF分量，第1行x(t)是发电功率原始数据。与晴天一样，雨天和多云天也由EEMD分解出的c1和c2分量重构成高频分量，再经Hilbert 变换后提取时频熵用于超短期功率预测；c3，c4和c5分量叠加重构成中频分量提取时频熵用于短期功率预测。

2.2 Hilbert变换提取时频熵

由Hilbert 变换可以求信号的瞬时频率，平稳信号的频率是定值，但对于不平稳信号，如由EEMD 分解光伏电站发电功率历史数据得到的各项IMF分量cj(t)，频率是关于时间的函数，用对应时间点上信号的瞬时频率表征信号特性[17]，对IMF分量cj(t)进行Hilbert变换的步骤如下。

1) 对每个分解得到的IMF 分量进行Hilbert变换：

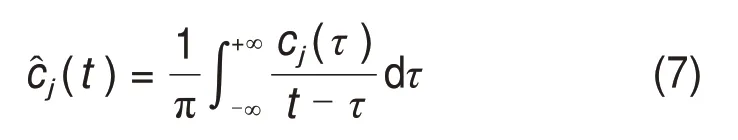
2)解析信号zj（t）如下：

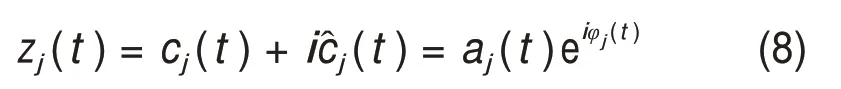
3)得到幅值函数aj(t)及相位函数φj(t)；

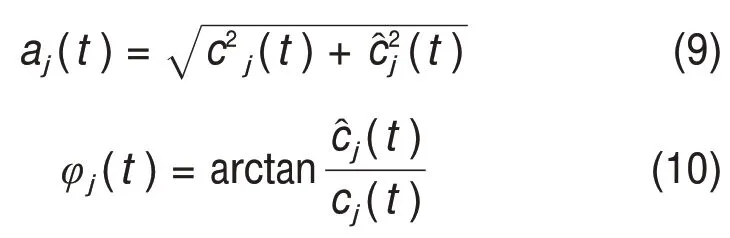
4)求出信号瞬时频率：

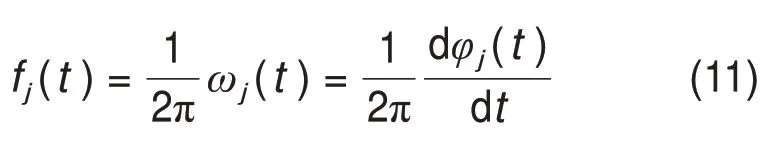
5)得到的瞬时频率与幅值(能量)呈现在时频域中就是能量分布图即Hilbert谱：

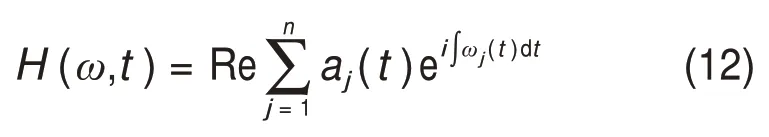
将晴天、雨天和多云天气的光伏发电功率历史数据由EEMD 分解后得到的高频分量与中频分量分别进行Hilbert 变换，求解出各发电功率历史数据记录点的瞬时频率与幅值。各点的频率及幅值变化情况呈现在时频域中的能量谱图即Hilbert谱如图3所示。各Hilbert谱图的差异主要体现在不同频率下能量的集中性及幅值上，图3(a)，(c)和(e)所示分别为晴天、雨天和多云天的高频分量，与对应中频分量的Hilbert谱图3(b)，(d)和(f)相比，能量明显更加分散，且雨天能量最低，3种天气条件下的中频分量都集中在约0.1 Hz 的较低频区域，其中晴天能量最集中、强度高且波动稳定，雨天与多云天能量分布形式及范围与晴天的相似，但辐射强度不稳定等导致图3(d)和(f)中能量分布波动较大，但多云天能量较雨天更高。针对各Hilbert谱图的差异性，可将其进行能量块划分，提取含有数据时频信息的特征参数时频熵[18]作为功率预测模型的输入，高频分量提取的时频熵作为超短期功率预测模型的输入，中频分量提取的时频熵作为短期功率预测模型的输入，辅助进行不同天气条件下短期与超短期的功率预测。时频熵计算式为

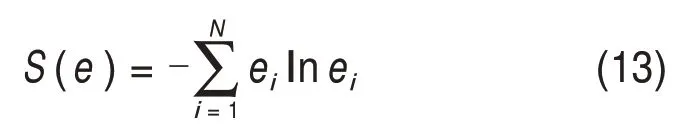
设整个时频谱平面的能量为W，将其均分成N块，每块平面上的能量为ki，则

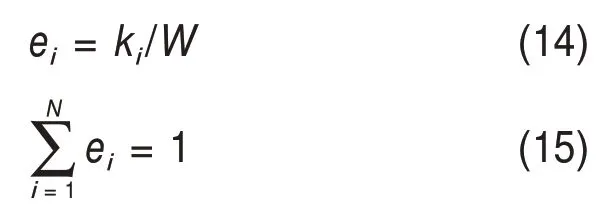
按式(13)计算各Hilbert 谱的时频熵，结果见表2。

3 预测模型构建及结果分析

3.1 BP神经网络光伏发电功率预测模型

RUMELHANT 等[19]于1986年 提 出BP 神 经 网络，目前广泛应用于风力发电功率预测及光伏发电功率预测领域，故采用BP神经网络作为验证此方法的预测工具，构建出基于时频熵和BP神经网络的光伏发电功率预测模型。BP 神经网络是一种单向传播的前馈神经网络，由输入层、隐含层和输出层组成，网络结构如图4所示。输入层和输出层节点个数由要预测的数据点个数决定。隐含层可以是1个或多个，为简化计算设置为1个，其节点个数与输入和输出层节点个数相关，计算隐含层最佳节点个数常用公式有以下几种：

表2 时频熵统计Table 2 Time-frequency entropy statistics

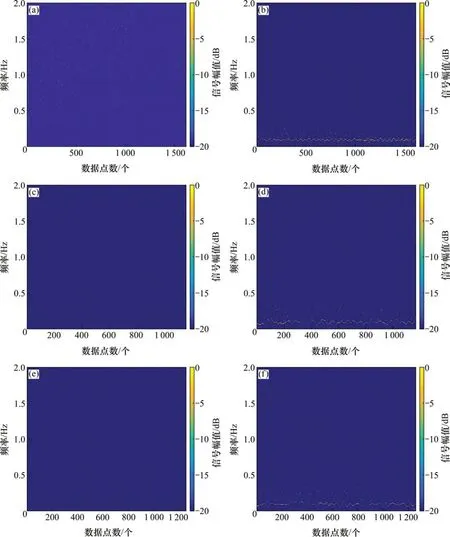
图3 不同天气光伏发电功率历史数据高频与中频分量Hilbert谱图Fig.3 High-frequency and intermediate-frequency component Hilbert spectrums of historical values of photovoltaic power generation in different weathers

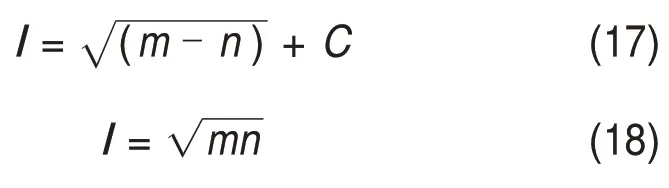
式中：l为隐含层节点数；n为输入层节点数；m为输出层节点数；C为调节常数，取值为1～10。可用公式确定范围再由试凑法选出使预测误差最小的节点数。

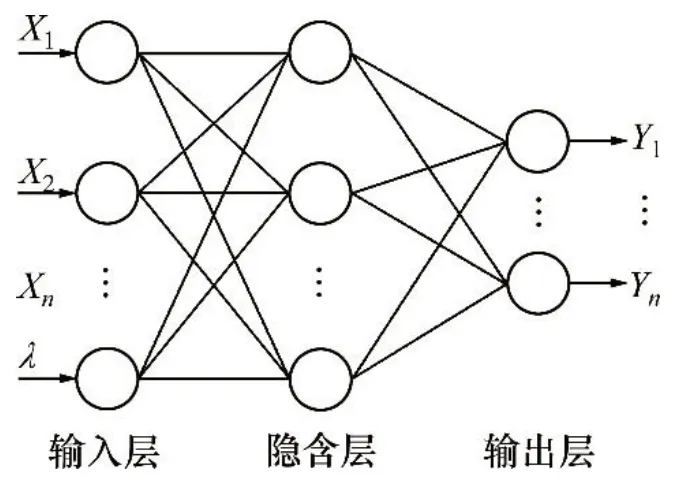
图4 BP神经网络结构Fig.4 Structure of BP neural network

采用湖北13 MW 光伏电站2017-09-25—2017-11-05 共45 d 的气象数据及发电功率(晴天15 d，雨天15 d，多云12 d)，另3 d 为复杂天气情况，不予考虑)，构建2 个预测模型，分别进行晴天、雨天和多云天气下短期和超短期光伏发电功率预测。以晴天为例，采集每天7:45至16:45的发电功率，每15 min 记录1 次，1 d 共37 个数据点，15 d 总共555 个数据点，将其按3.1 节的步骤进行EEMD 分解，得到高频分量与中频分量。进行短期功率预测时，BP 神经网络预测模型输入层节点共42 个，其中第1～37 个是EEMD 分解得到的中频分量某相似日内7:45至16:45的37个数据点，第38～41 个是预测日气象条件(温度、辐射强度、风速和相对湿度)，第42 个是表2中对应时频熵的均值，如晴天短期预测的均值取6.25，BP 神经网络输出层节点37个，为预测日当天7:45至16:45的37个发电功率数据点；隐含层采用单层，节点数根据式(16)至(18)取15～40，经多次试凑选取使预测均方根误差最小值25，则短期预测模型结构为42-25-37。进行超短期功率预测时，BP 神经网络输入层节点为13，节点1～8 的输入是EEMD 分解得到的高频分量相似日某2 h 内的8 个数据点，节点9～12的输入为气象数据，节点13的输入为表2中对应晴天超短期时频熵。输出层采用8个节点是为了预测某2 h 内的发电功率，隐含层节点为5 时预测的均方根误差最小，则超短期预测模型结构为13-5-8，BP 神经网络预测模型其他参数设置见表3。图5所示为时频熵和BP神经网络光伏发电功率预测模型的预测流程图。

3.2 预测结果分析

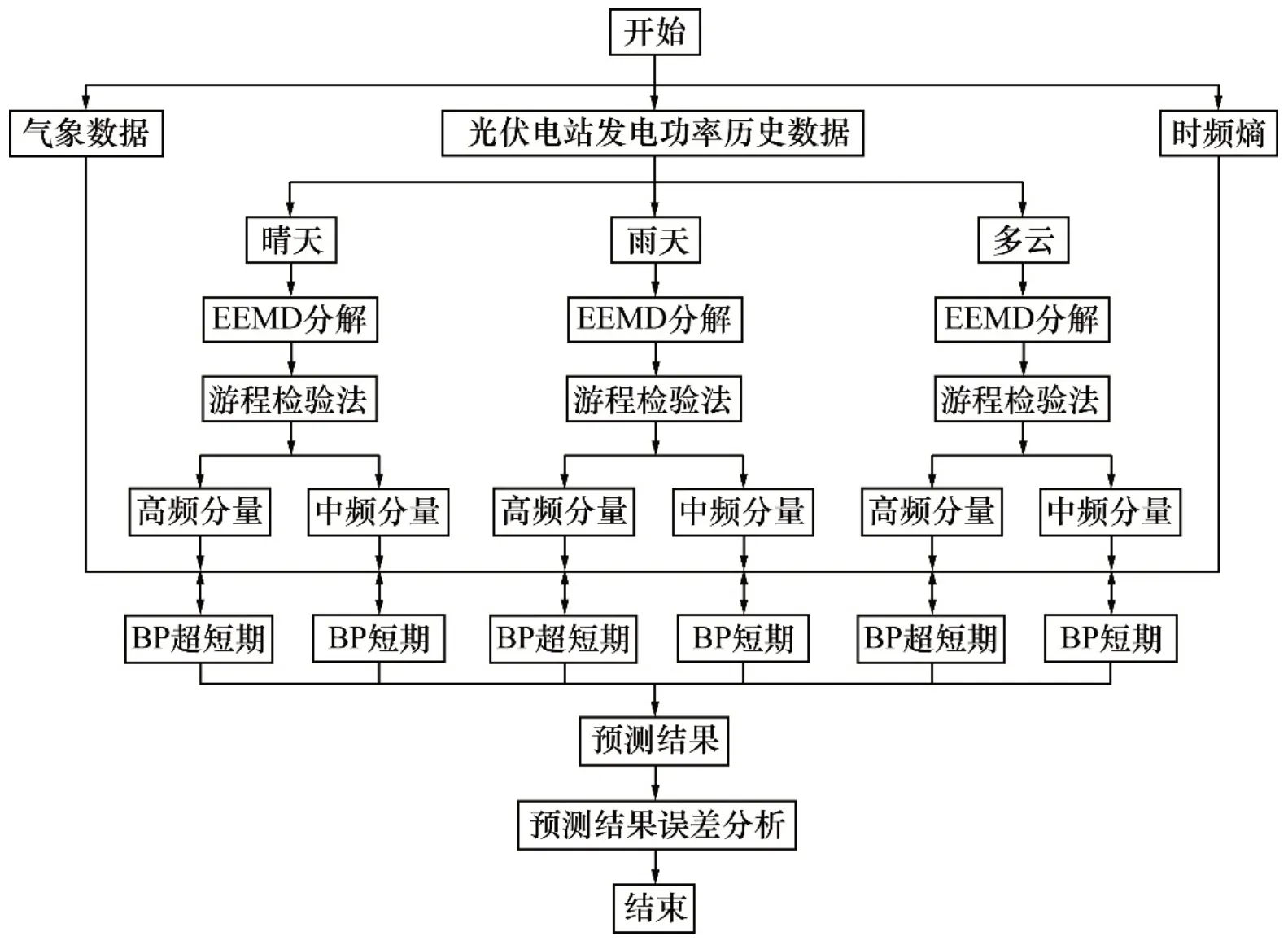
图5 光伏发电功率预测流程Fig.5 Flow chart of photovoltaic power generation prediction

表3 BP神经网络参数设置Table 3 BP neural network parameter setting

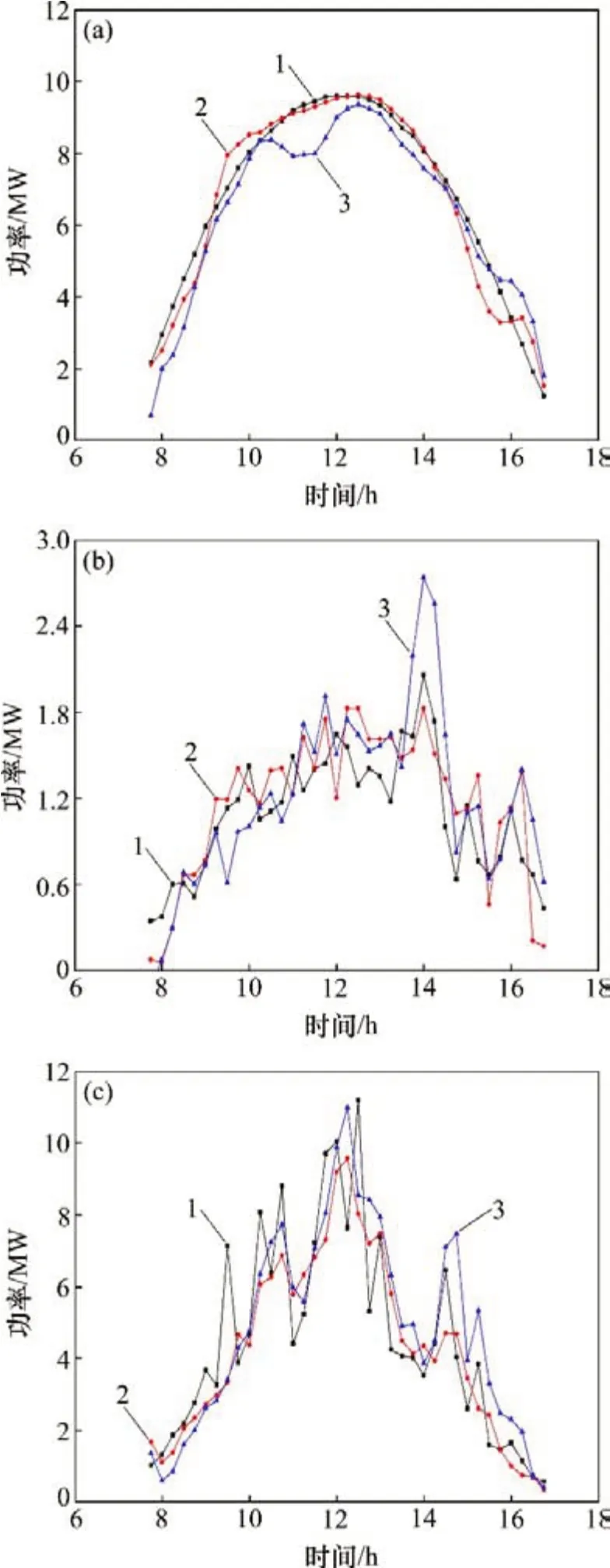
图6 短期光伏发电功率预测验证Fig.6 Forecast verification of short-term photovoltaic power

设置BP 神经网络预测模型后分别对晴天、雨天和多云天的短期和超短期光伏发电功率进行预测，从3 种天气类型中分别随机挑选1 d 来验证短期和超短期功率预测性能，其余数据按3:1分为BP神经网络的训练数据和测试数据。图6所示为采用2017-10-30(晴天)、2017-10-04(雨天)、2017-10-22(多云天)进行光伏发电功率短期预测验证的情况，图中直接预测曲线是仅使用气象数据的预测结果，作为文中加入时频熵和EEMD 分解后的分量进行预测的对比项，能明显看出用文中预测方法得出的预测曲线与实际值曲线更加吻合，预测效果更好。超短期预测时间为2 h，共8个预测点，图7所示为采用2017-10-26(晴天)、2017-09-26日(雨天)、2017-10-02(多云)随机挑选不同时间段的2 h进行光伏发电功率超短期预测验证的情况。

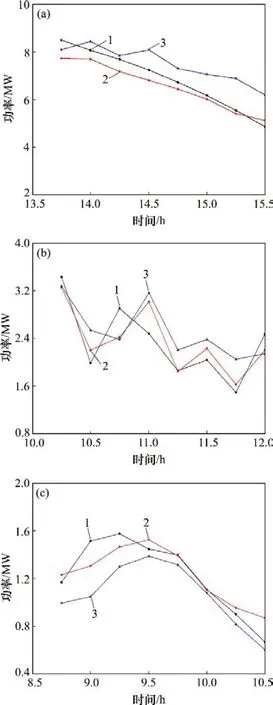
图7 超短期光伏发电功率预测验证Fig.7 Forecast verification of ultra-short-term photovoltaic power generation

表4 不同天气情况下短期与超短期光伏发电功率预测误差Table 4 Errors of shirt-term and ultra-short-term photovoltaic power generation forcasts in different weathers

检验预测模型的优劣需要进行误差分析，常用均方根误差s计算预测误差及相关系数R2计算预测精度，R2越接近于1，表明预测的准确率越高。s与R2的计算公式分别为：

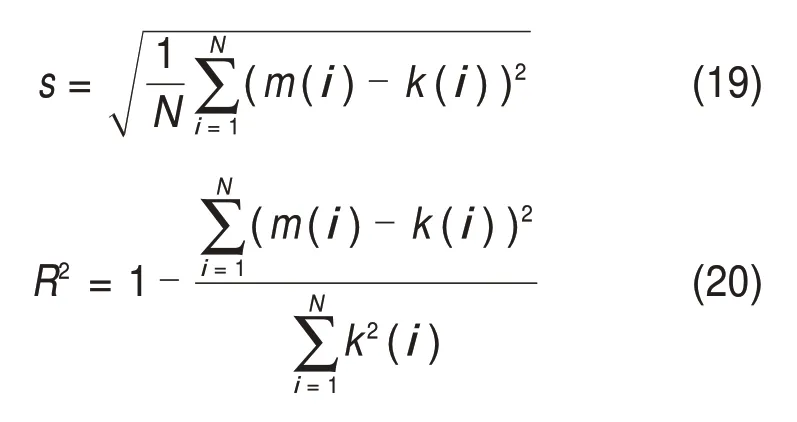
式中：m(i)为光伏发电功率实际值；k(i)为光伏发电功率预测值。将图5与图6中预测曲线的误差按式(19)和(20)计算后进行统计，结果见表4。采用时频熵和BP 神经网络对3 种天气短期与超短期发电功率进行预测，其均方根误差均比直接预测的小，预测准确率均相对更高。对比3 种天气情况，晴天预测准确率最高，短期与超短期的预测准确率都达到99%，因为与雨天和多云的发电功率历史值相比，晴天的规律性最强，波动最平稳，雨天与多云天发电功率在1 d 内波动大，变化不平稳，影响了预测准确率。

4 结论

1)提出一种基于EEMD-Hilbert 变换提取光伏发电功率历史数据时频熵，与EEMD 分解后的高频或中频分量结合进行光伏发电功率预测的新方法。用此方法进行BP神经网络短期和超短期光伏发电功率预测，得到较好的预测结果，得到的预测曲线能预知光伏电站发电功率，为电网合理分配电能、消峰填谷提供参考。

2)用此方法对晴天、雨天和多云天的光伏发电功率进行预测，超短期预测准确率分别为0.996，0.984 和0.991，短期预测准确率分别为0.995，0.944和0.931，均高于由气象数据直接预测的超短期准确率(0.987，0.967和0.964)、短期预测准确率(0.986，0.931和0.926)。

3) 雨天和多云天发电功率较晴天波动更大，短期预测准确率较晴天低很多，但超短期预测准确率相差不大，即它们的超短期预测准确率比短期预测准确率增加幅度远比晴天的大，预测准确率越高越有利于电网合理调度，提高光伏发电系统并网的优越性，故当雨天和多云天预测准确率不满足需要时，可适当缩短预测时间，以提高预测准确率。