基于质量分数垂线分布的粗骨料充填料浆特性表征

李立涛，陈得信，高谦

(1.北京科技大学土木与资源工程学院，北京，100083；2.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京，100083；3.金川集团股份有限公司甘肃，金昌，737100)

金川集团矿山在应用粒度小于5 mm 棒磨砂、粒度小于12 mm 破碎废石和粒度小于20 mm 戈壁砂等粗骨料进行下向分层进路充填时发现，粗骨料料浆在自流输送过程中，管道磨损和堵管的现象常有发生，同时充填体在采场内呈现层状结构，降低了胶结体强度和整体稳定性，给采矿高效安全生产带来隐患[1]。充填料浆在管输及采场流动堆积过程中，沿管道截面垂直方向及采场高度方向料浆质量分数分布不均匀是导致发生这种情况的根本原因[2]。理想状态下，当料浆达到一定质量分数时，在管道或者采场内垂直方向上的质量分数梯度为零，浆体呈均质流特性，有利于粗骨料管道及采场充填体的均匀分布[3]。因此，有必要对其现有充填料浆质量分数在垂线方向分布进行进一步识别及评价，从而针对充填料浆引起的质量分数分布不均匀影响因素，采取一定的方法，改善充填料浆的质量分数分布，减少管道磨损及堵管现象的发生，提高充填体的整体性。李国政等[4]从充填料浆达到理想均质流的受力角度出发，给出了充填料浆质量分数表达式及其影响因素，但有待于进一步验证。工业浆体管道大部分属于两相非均质流，管内固体垂向质量分数分布的均匀程度，与运行稳定性关系密切，虽然以管顶0.08D(D为管道直径)处的固体质量分数Sv与管轴心处的质量分数之比作为垂向质量分数分布的指标，但尚无统一认识[5]。扩散理论在悬浮颗粒质量分数沿垂线分布规律的研究中应用最广泛[6]，比如著名的Rouse公式[7-8]。混合理论基于扩散理论，试图从动力学角度研究悬浮颗粒质量分数分布，但由于固相和液相之间的作用力复杂，往往只列出其形式，然后进行简化、假设，最后还是回归到扩散理论[9]。重力理论认为固液混合体消耗的总能量应与清水阻力所消耗的能量加上水流悬浮颗粒的能量(即悬浮功)相等，最终还是得到了一个形式上与扩散方程十分相似的微分方程。在此基础上，演变的理论还有能量理论、相似理论及随机理论[10-11]，各种理论虽然出发点不同，但从其最后所得结果来看，都是(或接近)扩散理论。倪晋仁等[12]依据扩散理论，综合考虑垂向脉动速度所服从的概率分布规律来研究质量分数分布，提出质量分数分布统一公式，能较好地概括各种理论公式，但公式不可控因素太多。以上研究均未给出影响因素及质量分数分布具体计算公式，本文作者在扩散理论的基础上，分析充填料浆固粒受力，结合垂向脉动速度的概率分布，推导充填料浆质量分数垂线分布公式，以期获得一种评价充填料浆工作特性新方法并且能通过改变其影响因素来改善料浆特性。

1 充填料浆固粒连续方程

颗粒之所以能够悬浮，是水流紊动扩散及颗粒重力综合作用的结果，这就是颗粒扩散理论所依据的基本概念，扩散理论在悬浮颗粒质量分数沿垂线分布规律的研究中应用最广泛[13-15]。充填料浆中固相颗粒(骨料与胶凝材料)在液相中的不均匀悬浮，造成了充填料浆在管道中或采场内垂线方向质量分数分布的不均匀。

因此，若充填料浆中固相颗粒在液相中处于平衡状态，则所满足的连续方程可表示为

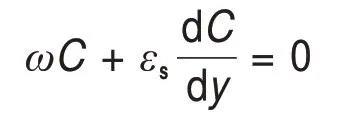
即：

式中：εs为颗粒扩散系数；C为固粒质量分数；ω为固粒在液相中的沉降速度。

因此，当给定充填料浆质量分数一定时，对充填料浆质量分数在垂线方向上的分布规律研究的关键是沉降速度ω及扩散系数εs的准确表达。

2 充填料浆质量分数垂线分布模型

2.1 固粒沉降速度

在粗骨料充填料浆中，细颗粒间的“自絮凝”作用导致屈服应力的产生。因此，粗颗粒在浆体中除受重力G和浮力Ff外，还受到浆体的剪切阻力Fz作用[16-17]。将充填料浆中的粗骨料等效为理想球形颗粒，则其受力状态如图1所示。由于粗颗粒的密度相对较大，当浆体对其的剪切阻力较小时，极易发生沉降，导致充填料浆质量分数在垂线方向存在一定的质量分数梯度与分布。可采用如下运动方程来表示颗粒运动速度和受力之间的关系：

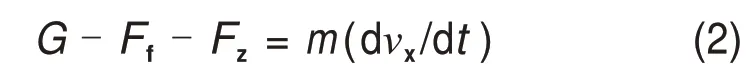
式中：G为固体颗粒重力；Ff为颗粒在流体中所受的浮力；Fz为液体作用于颗粒的阻力；dνx/dt为颗粒运动的加速度。

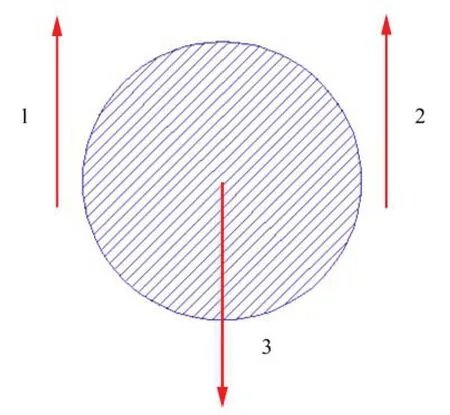
图1 固粒受力状态Fig.1 Force condition of solids

由阿基米德原理可知，固粒在液体中的有效重力等于该颗粒在真空中的绝对重力减去同体积的液体重力，则有

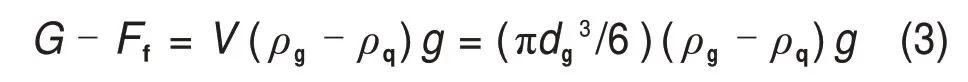
式中：ρg为固粒表观密度(骨料和胶凝材料混合料的密度)；dg为固粒等效直径；ρq为充填料浆的密度。

目前，实验与理论分析相结合，可知阻力F和固粒直径(dg)的平方成正比，与固粒运动的相对流速(νx)的平方成正比，与密度(ρq)成正比，因此，阻力F的计算式[18]为

式中：ψ为总阻力系数，它取决于雷诺数Re及颗粒形状，对于理想光滑的球形颗粒，其值为1.0，对于非球形颗粒，取1.2～2.0[19]。

对于球形颗粒，dg=d，d为球形颗粒直径；对于非球形颗粒，和dmin分别为体系中颗粒最大粒径和最小粒径；xi为粒径i在粒径分布体系中的分计，%；di为各级粒径。

惯性力Fg=G，将式(3)和(4)代入式(2)，整理得

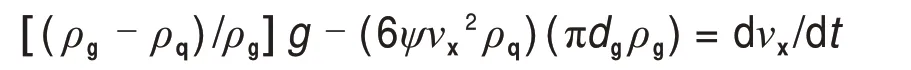
当充填料浆进入采场之后，固体颗粒经过一段时间的运动，所受外力达到平衡，在惯性作用下，达到等速沉降，这时，等速下沉速度简称为沉降速度(用ω表示)，有dνx/dt=0，求解上式可得沉降速度：

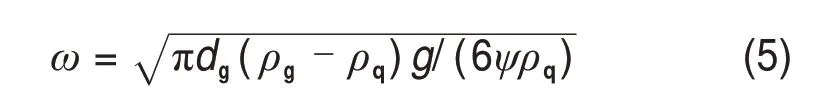
2.2 固粒垂线方向扩散系数

对管道内的充填料浆，垂线上任一点，若颗粒上小交换质量守恒，则可得扩散方程：

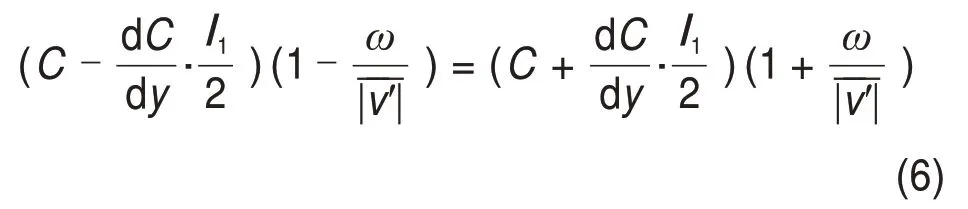
式(6)结合式(1)可得，

式中：v'为垂向脉动速度，对于，若v'服从正态分布，即

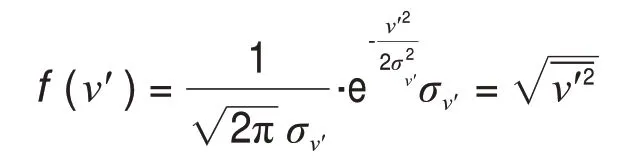
则

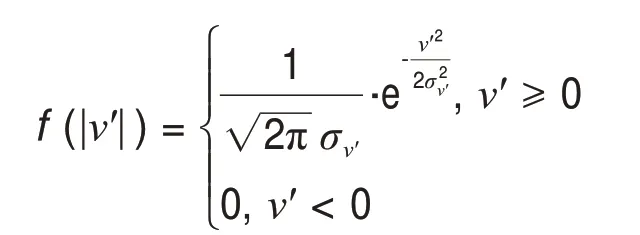
式(1)可转换为

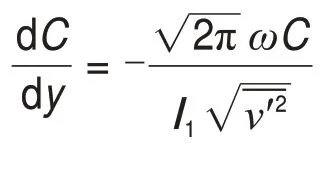
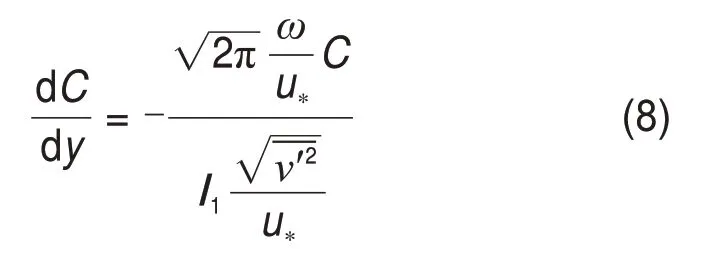
令

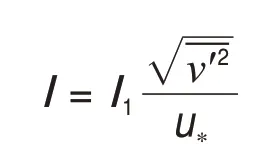
则l的变化只与l1的选取有关，而l1则是与固液相特性及位置有关的量[12]。为了考虑颗粒特性的影响，广义地可以选

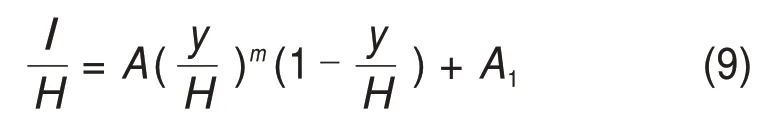
式中：A为系数；m为指数；A1为常数。通常A1和m可取为零，A可取为1。

2.3 固粒摩阻流速

摩阻流速又称“壁面剪切流速”，其值一般为壁面切应力与流体密度之比值的平方根[20]，则

2.4 质量分数垂线分布公式

在不考虑料浆所处空间尺寸效应影响下，将式(5)，(9)和(10)代入式(8)，积分后可得充填料浆质量分数垂线分布公式：

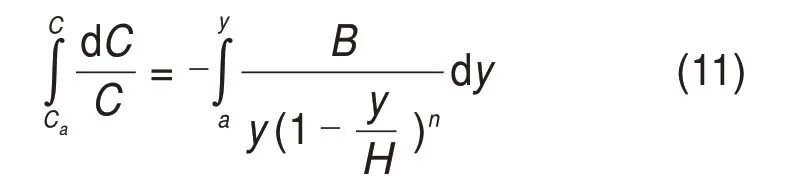
式中：Ca为距料浆底部高程y=a处的固粒质量分数；n为反映固液两相特性对颗粒跳跃特征长度影响指数； 充填料浆自由沉降时，B=

2.5 充填料浆质量分数分布影响因素分析

2.5.1 颗粒跳跃特征长度影响指数

综上所述，将方程式(11)作为充填料浆质量分数垂线分布公式。由于n的取值范围不是很大，而当n取任意值时的级数表达形式相对有些复杂且精度还依赖所取级数项，倪晋仁等[12]研究后建议可以利用当n为正、负整数及n为0，0.5 和1.0 等特殊值时可积这一优势，对n为任意值时不可积的情形直接做内插。

当n=0时，有

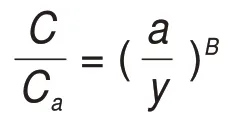
当n=0.5时，有

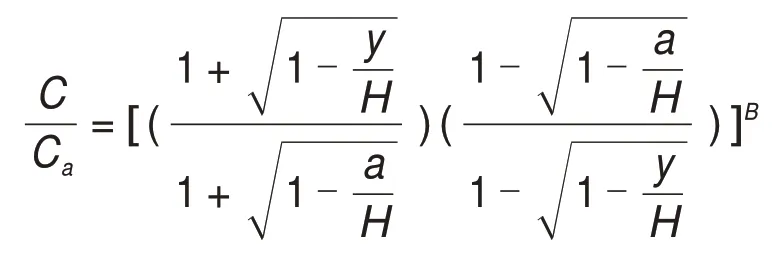
当n=1.0时，有

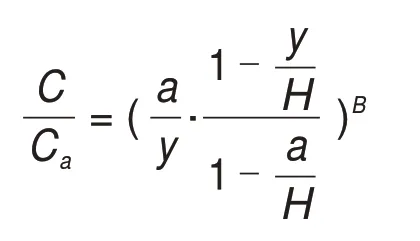
2.5.2 材料物化特性影响因素

若n一定，Ca为料浆质量分数时，C/Ca越接近1，充填料浆则越趋向于均质流，质量分数在垂线方向的分布越均匀。由方程式(11)可知：影响充填料浆质量分数垂线分布的因素主要有固粒粒径dg、固粒密度ρg、料浆密度ρq、初始切应力τ0、固粒粒形。充填料浆初凝前，在管道输送或者采场堆积流动时，固粒部分包括骨料与胶凝材料，因此，若改善充填料浆的质量分数分布，则可从dg入手，即改变骨料或者胶凝材料粒径分布。由于不同料浆质量分数的初始切应力τ0存在明显差异，在满足料浆可输送的条件下，结合充填倍线，也可通过优化料浆质量分数来改善质量分数的垂线分布。

3 实例讨论

为验证充填料浆质量分数垂线分布模型对料浆工作特性表征的合理与可靠性，考虑影响质量分数垂线分布的因素，结合金川现有充填料浆参数，进行不同质量分数、不同充填材料级配的充填料浆流变特性和工作特性试验。

3.1 试验材料及方法

3.1.1 充填材料

试验用棒磨砂骨料取材于金川矿区周围的戈壁卵砂石。采集的戈壁砂首先经由筛分工序，获得粒度大于5 mm部分在金川公司砂石厂通过“两段一闭路”的破碎工艺和棒磨工艺后，加工成粒度小于5 mm棒磨砂骨料，将棒磨砂烘干后，获得其密度为2.68 g/cm3。试验用废石骨料取自金川龙首矿破碎废石，经由颚式破碎机破碎筛分，获得粒度小于12 mm 的废石粗骨料，测定其密度为2.82 g/cm3。试验用水泥为金昌水泥厂为矿山充填所生产的非标矿用38.5水泥，其密度为3.01 g/cm3，各材料粒径分布见图2。

3.1.2 试验方法

依照金川矿山工业充填料浆参数，胶砂比(即充填料浆中胶凝材料与骨料的质量比)为1:4，选择料浆质量分数为78%，80%，82%和84%，为研究充填材料不同粒径分布对料浆质量分数分布的影响，选择废棒比(废石与棒磨砂的质量比)为3:7，2:8 和1:9。每组充填料浆在充分搅拌均匀后进行流变特性测试，以便测得屈服应力τ0。试验采用国Brookfield公司生产的R/S+SST流变仪，选择30/15桨式转子，转速设置初始值为20 s-1，终值为120 s-1，检测次数为100次，试验方案及结果见表1。

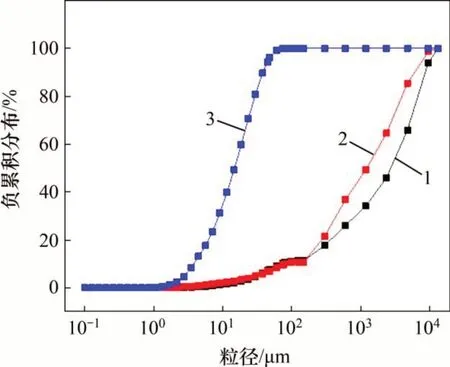
图2 充填材料粒径分布Fig.2 Particle size distribution of filling materials

参考混凝土测试方法，测定料浆的扩展度、泌水率等参数。当塌落度大于22 cm时，其不能准确地反映料浆的流动性，故用塌落扩散之后的料浆平均直径扩展度来表示流动性指标。测量时，用钢尺量取料浆扩散后不同位置处的直径，取其平均值。料浆泌水率是指料浆静置60 min 后的泌水清水质量与总含水质量的比值。

3.2 结果与讨论

3.2.1 料浆工作特性变化规律

图3所示为料浆工作特性随质量分数变化曲线，由图3(a)可知：在相同废棒比下，料浆的扩展度随质量分数的增加而减小，当料浆质量分数为78%～80%时，料浆扩展度下降幅度较小。当料浆质量分数高于80%时，随料浆质量分数的增加，扩展度急剧减小，说明当料浆质量分数大于80%时，对废石棒磨砂混合骨料充填料浆而言，料浆质量分数的增加对料浆的工作特性存在明显影响。在同一料浆质量分数下，料浆的扩展度随废棒比的减小逐渐增大，相较废棒比由4:6到3:7，废棒比由3:7 减小为2:8 时扩展度变化较小，混合骨料的不同配比引起充填材料特征粒径发生改变，从而引起料浆工作特性的变化。图3(b)所示为泌水率随料浆质量分数变化曲线。当料浆质量分数大于80%时，泌水率下降幅度较大，废棒比3:7 和2:8的泌水率相差较大；当料浆质量分数为80%时，其泌水率相近。当废棒比为3:7，料浆质量分数为78%与80%时，泌水率相差较小。

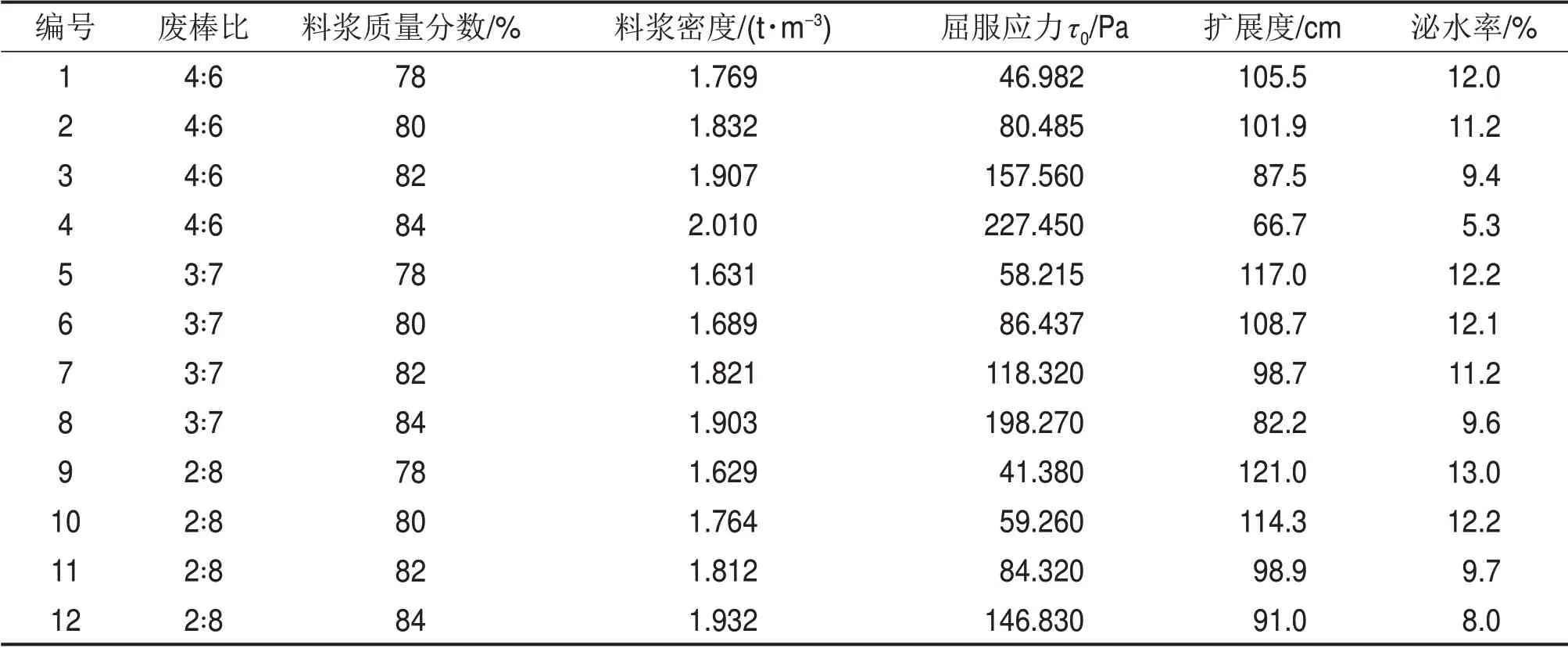
表1 废石-棒磨砂混合骨料充填料浆试验结果Table 1 Test results of filling slurry with waste rock-bar abrasive mixture

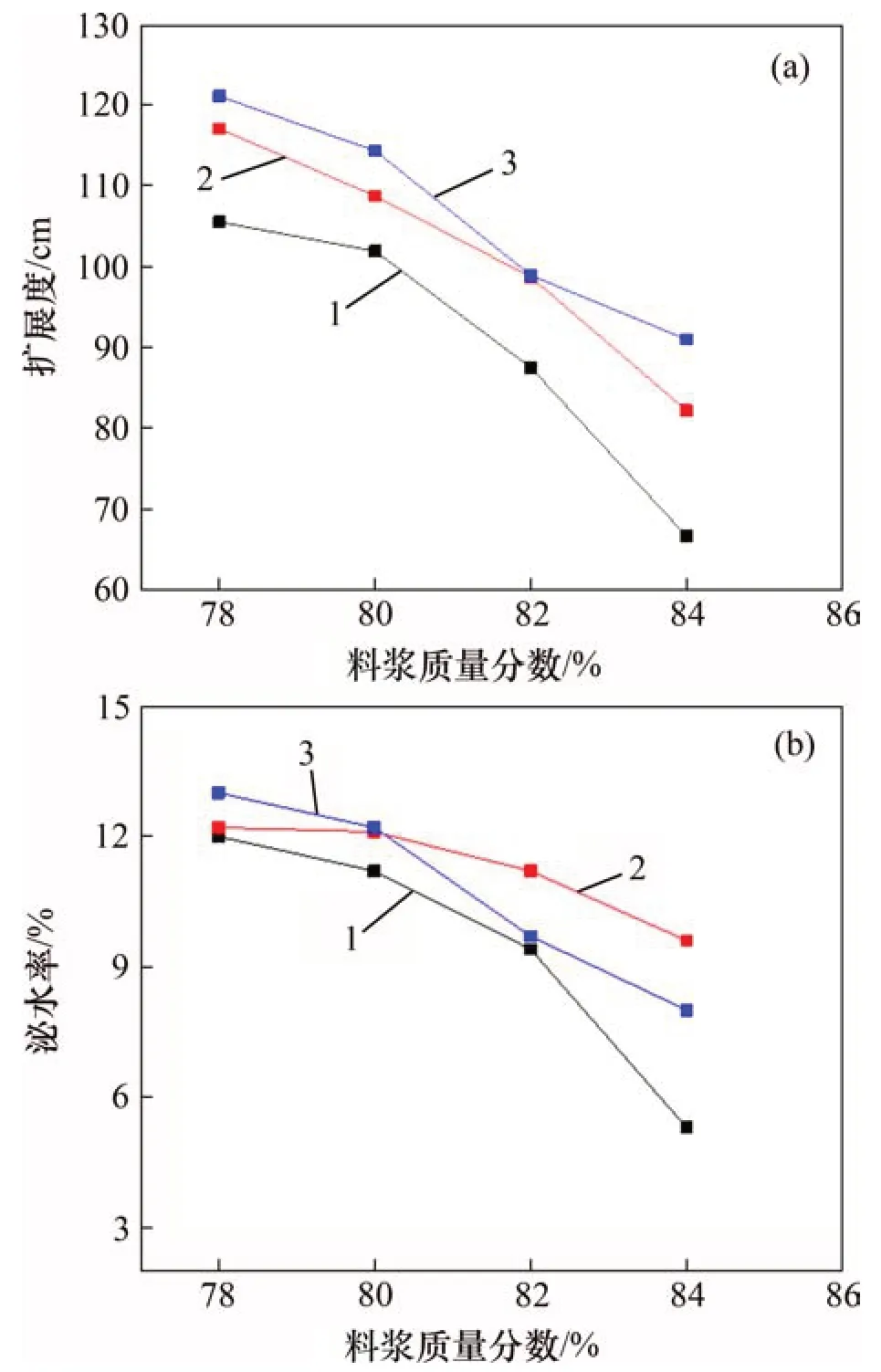
图3 料浆工作特性随质量分数变化曲线Fig.3 Curves of slurry performance with mass fraction

3.2.2 质量分数分布变化影响研究

废棒比导致混合充填材料等效加权平均粒径的不同，由充填材料粒径分布计算可得，当废棒比为4:6，3:7 和2:8 时，混合充填料的等效粒径dg分别为3.785，3.605 和3.425 mm。为了控制变量，将质量分数垂线分布公式中的Ca取距料浆底部高程0.1处的固粒质量分数C0.1。采用式(11)计算每组试验的充填料浆质量分数垂线分布数值，绘制不同n的质量分数垂线分布随深度变化曲线。图4所示为不同n时平均质量分数分布随深度变化规律曲线。从图4可见：随n的变化，质量分数分布数值有差别，但其变化趋势一致。距离液面越近时，不同n的质量分数分布呈增大趋势。总体来说，n引起质量分数分布的数值变化幅度在误差范围内，对表征充填料浆工作特性影响不大。

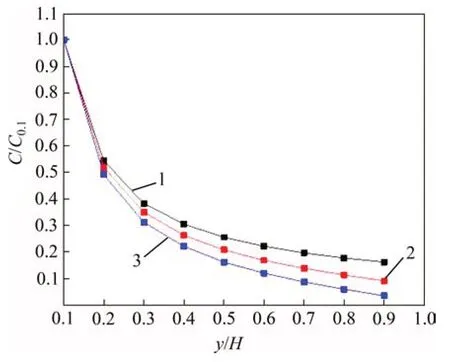
图4 不同n时质量分数分布曲线Fig.4 Curves ofmass fractiondistributionwithdiffrernt n

当n=0.5时，不同废棒比下料浆质量分数分布曲线如图5所示。从图5可知：在相同条件下，料浆质量分数垂线分布C/C0.1随质量分数的增加而增大，当料浆质量分数为78%～80%时，质量分数分布曲线间距较小，表明质量分数分布在垂线方向分布变化较小；当料浆质量分数大于80%时，间距增大，垂线方向不同位置质量分数分布增加幅度较大，这与扩展度数值变化规律相反，但与所表征的料浆工作特性一致，即随料浆质量分数的增加，料浆质量分数垂线分布逐渐趋向均匀，流动性降低；当料浆质量分数大于80%时，质量分数垂线分布随废棒比的减小而减小，与料浆质量分数为84%时相比，82%时质量分数分布随废棒比的减小幅度较大；当料浆质量分数小于80%时，质量分数垂线分布随废棒比的减小先增大后减小，当废棒比为3:7时，质量分数分布达到最大，此时泌水率也接近。通过质量分数垂线分布理论公式所获得的充填料浆工作特性变化规律与工作特性试验结果一致，因此，质量分数垂线分布是可以表征或者评价充填料浆工作特性，在满足矿山充填料浆流动性的前提下，可改变影响质量分数垂线分布的因素即料浆质量分数、固粒密度与粒径，最终改善质量分数垂线分布C/Ca的数值，该数值越接近1，则质量分数分布越均匀。

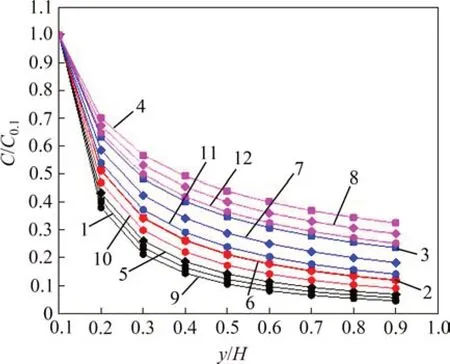
图5 不同配比料浆质量分数分布曲线Fig.5 Curves of mass fraction distribution with differentwaste rod ratios

3.3 存在问题及讨论

对于充填料浆质量分数垂线分布公式，随n变化对质量分数分布影响不大，但若n一定，则C/Ca是一个确定公式，而不必经过特殊值内插获得，对于定量研究充填料浆的质量分数分布具有指导意义，因此，参数n变化规律的确定值得进一步研究。

4 结论

1)以扩散理论为基础，结合粗骨料充填料浆固粒受力，推导出充填料浆质量分数垂线分布公式。影响充填料浆质量分数垂线分布的因素主要有固粒粒径、固粒密度、料浆密度、初始切应力、固粒粒形。

2)当料浆质量分数小于80%时，质量分数垂线分布值随质量分数的增加而增大，质量分数分布在垂线方向上变化较小；当料浆质量分数大于80%，曲线间距增大，垂线方向不同位置质量分数分布增加幅度较大，与扩展度所表征的料浆工作特性一致，随料浆质量分数的增加，料浆质量分数垂线分布逐渐趋向均匀，流动性降低。因此，采用质量分数垂线分布公式评价充填料浆特性时，若n一定，C/Ca越接近1，充填料浆则越趋向于均质流，质量分数在垂线方向的分布越均匀。

3)质量分数垂线分布公式可表征与评价充填料浆工作特性，在满足料浆可输送的前提下，可改变影响质量分数垂线分布的因素，即料浆质量分数、固粒密度与粒径，进而改变质量分数垂线分布的数值，最终改善料浆工作特性。