一种变邻域搜索与人耳掩蔽音乐生成方法
梅 林,肖兆雄,沙学军
(哈尔滨工业大学 电子与信息工程学院,哈尔滨 150080)
音乐在日常生活中扮演着独特角色,人们利用音乐或释放压力、表达情感、寻求共鸣,或尽情享受音乐带来的美的体验.随着生活水平的不断提高,只要稍加练习,普通人也能演唱或弹奏出优美的旋律,但相比之下作曲的门槛显然更高.编写一首乐曲往往分为旋律、风格、速度、调性与结构、和声与乐器等部分[1],而且乐曲的各个部分不是完全正交,而是相互关联的,例如一首歌的旋律往往决定了它的风格,而风格又在一定程度上影响了速度;乐句往往是小节的重复或变体等.因此在过去作曲属于少数有天赋的人的工作,同时编写一首好的乐曲也得益于作曲家的丰富经验.
随着计算机技术的发展,研究人员试图从两个角度利用计算机帮助作曲:一方面,协助有经验的作曲家,完成一部分繁琐的可重复性工作,使其专注于创造性的艺术;另一方面,使普通人也能够从轻松谱写简单的乐曲开始,一步步培养人们作曲的能力与对音乐的兴趣,使人们更加了解谱曲背后的原理,从而为作曲领域提供更多可能.本文着重研究的是无需或仅需少量专业知识的基于计算智能的音乐生成方法.伴随着音乐市场的迅猛发展,作曲的专业方法与水平也在迅速攀升,基于变邻域搜索与掩蔽效应的音乐生成方法能深度挖掘乐谱的潜能,通过人机交互充分调动音乐爱好者,尤其是青少年对音乐创作的积极性.
1 音乐生成领域研究概况
1.1 研究概况
从1959年Hiller与Isaacson首次在电子计算机上编写音乐生成算法[2]开始,人们一直尝试利用计算机代替或协助操作者完成作曲工作.音乐生成算法大致包含两大类别:传统算法与机器学习算法.传统算法往往通过对音乐数据的特征提取建立数学模型将音乐参数化[3],或使用音乐编曲规则建立网络结构并填充先验知识库进行建模[4];机器学习算法往往使用MIDI格式文件,通过构建神经网络,如递归神经网络(Recurrent Neural Network, RNN)、卷积神经网络(Convolutional Neural Network, CNN)、长短时记忆(long Short Term Memory, LSTM)网络等对音乐进行训练[5-10],随后通过随机初始化参数的方法生成音乐.
尽管基于机器学习方法的音乐生成算法种类丰富,并且充分利用的模型或网络的计算性能,但仍存在以下问题:
1)训练样本基本采用MIDI格式的音乐文件,该格式的音乐文件数据量小,易操作,但其音乐形式往往较为陈旧,无法体现音乐的流行性;
2)现有的基于机器学习的音乐生成系统网络往往移植于在自然语言处理或图像处理取得成效的网络,几乎不存在为音乐信号专门设计的神经网络结构.因此无论是系统的输入输出还是参数调节都存在着一定的局限性;
3)绝大多数的音乐生成模型在生成阶段采用的是白噪声信号作为输入,不符合一般的作曲规律;
4)生成出的音乐样本往往在长时间范围内不具备和谐性,且一般只有一种乐器,音乐形式较为单调.
1.2 本文所采用的方法流程
本文设计以下结构用作音乐生成,如图1所示.输入阶段为时域音乐波形,经过基于音高显著度的旋律提取与基于人耳掩蔽效应的时域音符分块后映射到音符域以便人为调整,随后输入训练模型中获得动态范围、二次折叠基音等训练数据.在生成阶段使用基于变邻域搜索的音乐生成算法迭代生成乐谱,最后从乐器库中选择乐器完成音乐片段的制作.整个过程从输入到输出都可以生成乐谱与时域波形文件以便人工增删与标注,人机交互的思想贯穿其中,有助于充分调动操作者的积极性.下面分为训练阶段、生成阶段与乐音模拟三个部分对整个系统做介绍.

图1 本文音乐生成系统结构
2 训练阶段
2.1 训练输入与预处理
输入音乐训练阶段的输入x(t),它以4个小节为单位,可以是一段乐器的独奏,也可以是一段人声哼唱.在后续的处理中将对x(t)重新定位,音符起始位置位于t=0处.

为调动操作者的积极性与创造力,本文所述方法有意对频谱进行模糊处理.降低部分基频提取算法的复杂度,并采用余弦加权算法,帧内加权算法为
(1)


图2 基于音高显著度的旋律检测示意
由图可知该算法基本可准确检测旋律线,但会偶尔出现旋律过低的情况,可用简单的算法解决.但使用本文的预先加权算法将会有意使其中两个音符的高度降低,通过谱表可视化与试听即可手动在谱表中调整音高,达到培养操作者的乐感的目的.
2.2 训练参数
基于现有的乐理知识,本文将训练参数设置为式(2)所示,式中第1项为记数符,用于标示已训练样本的数量,前3列为专业乐谱参数,后4列为将乐谱进行两次折叠后获得的基本乐谱参数,用于描述乐谱在较长时间内的连贯性与变化.将频谱折叠后处理属于本文的试验性操作,初步选取4个基本乐谱参数进行分析,不至于使系统过于复杂.具体参数名如表1所示.
(2)

表1 训练用乐谱参数
以数个表中基本参数为例,基音为乐谱的第一个音,动态为音符的整体变化程度,丰富度为音符出现的数量,速度为音符间平均间隔.
以其中一个二次折叠参数为例,二次折叠动态1如式(3)所示:
Ndyna4N,1=∑(|diff(E4(1,i))|).
(3)
式中E4(1,i)为将乐谱E(i)二次折叠后的乐谱第一行,求导操作将跳过E(i)=0的非音符点.在获取上述参数后,可继续添加训练样本.理论上添加风格不同的音乐会使训练用乐谱参数趋于二者平均值,因此可对训练结果进行加权,使整体的训练结果偏向一特定风格.此外上述参数也可作为评价标准对后续生成的音乐片段进行打分.
3 生成阶段
3.1 变邻域搜索算法
变邻域搜索算法属于具有通用算法构架的元启发式算法,这类算法一般用于求解NP-难问题.变邻域搜索算法在寻找局部最优解的迭代过程中不断改变邻域,算法的核心在于邻域结构的定义.变邻域搜索算法在音乐生成领域的相关研究极少,但由于变邻域搜索算法的步骤与作曲工作中旋律的确定十分相似,且迭代终止条件可以与人工判别相结合,因此本文选择变邻域搜索算法作为音乐生成迭代算法.
在介绍变邻域搜索算法前,首先对优化问题及其相关定理进行说明.优化问题如下式定义:
min{fi(x)}
s.t.hj(x)≤bj
(4)
式中:x∈F,F⊆S;i=1,2,…,m;j=1,2,…,n;S为解空间;F为解集;x为可行解;fi为目标函数;hj为约束条件函数.在音乐生成问题中,x为音符位置,S为有限空间,则音乐生成问题为组合优化问题.

将变邻域搜索算法移植到音乐生成系统中,需要改进的有以下部分:1)邻域结构D(x)需要根据乐理知识事先进行规定,效果近似于常规作曲时对乐谱的修改;2)在迭代过程中,邻域结构D(x)可人为进行改变,保证数个音符不发生变化;3)目标函数的值取最小并不意味着旋律最动听,因此需要根据人耳试听辅助判断任意解x是否为局部最优解,或人工调整解的形式.
基于以上问题,本文提出的基于乐理知识的变邻域搜索算法做出了以下改进:1)根据基本作曲知识将邻域结构转化为变邻域搜索操作,包含变调、删减音符与增加新音符三种;2)在迭代过程中可人为锁定部分音符,改变邻域结构;3)迭代停止条件由目标函数的计算与人工试听进行联合判决.
变邻域搜索算法流程如下:
1)规定目标函数fi,根据乐理知识设计x的邻域D(x),规定最大迭代次数km与每次迭代搜索操作;
2)随机生成或人工输入初始值x;
3) 随机选取D(x)内的s个点x1,x2,xs,令满足fi(x)最小点为中心,并可以人为固定部分音符值,从而生成新的D(x);
4)重复上述操作直至达到最大迭代次数或人工停止.
本文提出的基于乐理知识的变邻域搜索操作包含变调、删减音符与增加新音符三种,算法流程见图3.每次迭代首先随机生成搜索长度RrandL=2n,n=0,1,2、搜索起始位置RrandP∈[1,64-randL+1],与搜索操作RrandO=1,2,3,其中RrandL,RrandP共同表示邻域区间,RrandO=1,2,3分别对应变调、删减音符与增加新音符3种操作.当任意待处理位置有Ccell(1,i)=′1′,即被锁定时,重新生成以上参数,随后依照训练参数表与RrandO对音乐片段进行处理,并计算参数矩阵KdataG4×7通过预先设定好的代价函数矩阵KdataC4×7计算得分:
SScore=∑(|KdataG-KdataN|·KdataC).
计算乐谱的变化程度后,对乐谱进行综合打分.例如动态越高说明音符更富于变化,代价函数得分越低说明与训练数据越接近.若此次搜索的结果在门限外,则再次重新生成RrandL,RrandP,RrandO并重复以上操作直到满足条件为止.
乐谱的得分并不能完全反映音乐片段是否动听,只能从一定程度上约束乐谱的生成规律.例如一个乐谱动态范围很大,可能是旋律紧凑动人,也可能是音符杂乱无章的排列.若要保证每次迭代的代价函数得分变低,结果往往是一个或一段音符持续时间的删减.经过多次测试后,本文设计了一个得分门限(20%),虽然迭代后的乐谱可能代价函数得分变高,但如果在门限内则保留乐谱,即保证了乐谱不至于出现过多删减,同时也不会出现过于不和谐的音符.
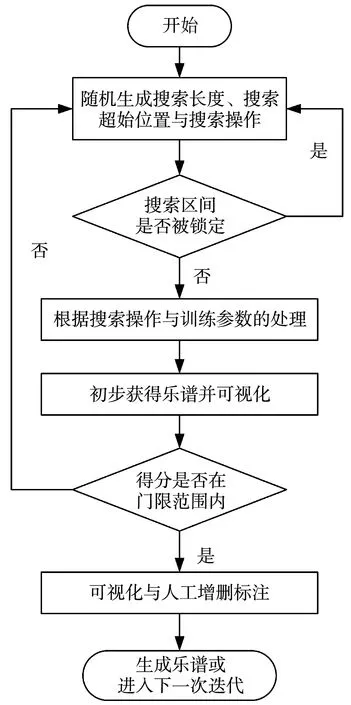
图3 变邻域搜索算法流程图
迭代后的乐谱通过GUI界面进行可视化显示,操作者可通过试听判断乐谱中动听的部分并进行音符的增删与标记Ccell(n,i)=′1′,若Ccell(n,i)=′1′则在接下来的迭代中将跳过被标记的音符,随后重复上述步骤对乐谱进行迭代,计算机迭代与人工评价与处理交互进行,直至生成令人满意的乐谱G(i).
3.2 后期处理
生成音乐片段可保存为wav格式文件或表格文件,可用于后续的音乐生成或添加伴奏、修饰与调节速度等后期处理操作.本文提供一种根据所生成乐谱的二次折叠信息G4(j,i),i=1,…,16,j=1,…,4添加伴奏与鼓点的方法.首先根据G4(1,i),i=1,3,5,…,15确定伴奏的音符起始位置与音高,再根据G4(j,i)的二次折叠动态参数对音高进行变调,最后根据Bbpm与G4(j,i)中音符出现的位置添加鼓点.文中的主旋律、伴奏与鼓点均通过乐音模拟方法生成和选取.
4 乐音模拟
4.1 常见乐器的分析与分类
一种乐器的乐音一般由声源经过共振腔,再经过外部环境到达人耳.本文对几种常见乐音模拟算法(基于物理模型的弦振动仿真、基于电声类比的共振腔模拟[11]与基于二维数字波导的乐音合成[12]等)进行分析与总结,以基于物理模型的弦振动仿真为例,可以用一个偏微分方程及其边界条件来描述音乐信号的时间序列:
(4)
式中:t与x为时空坐标,y(x,t)为振动偏移量,E为弹性模量,T0为弦两端的标称张力,ρ为材料密度,A为弦的横截面积,I为惯性矩,d1为与时间相关的阻尼,d3为与频率相关的阻尼.式(3)的边界条件为
y(0,t)=0,y(L,t)=0,
(5)
(6)
忽略变换求解过程,其结果为基频与谐波的叠加.以吉他尼龙弦为例,对模型进行仿真,仿真结果的时域信号幅值较小且呈指数衰减,与实际情况类似;其频域结果在基频与谐波出现了较为明显的峰值.基于电声类比的共振腔模拟与基于二维数字波导的乐音合成等研究结果与上述结果类似,输出结果为频域共振峰图.通过对常见乐器的频域幅值与时域包络的试听与分析,并结合上文的研究结果,将乐器分类为弦乐器、体乐器和混合乐器3种.
4.2 乐音参数化与模拟生成
本文将乐器的发声模式简化为图4所示结构.

图4 模拟乐器发声结构
将乐音模拟分为激励源S、频谱F(a,f)与时域包络A(b,t)三部分.其中若激励源为白噪声(对应体乐器),频谱F(a,f)可用多个带通滤波器组表示,若激励源为弦振动(对应弦乐器),频谱F(a,f)可与激励源加权混合表示.通过根据需求确定相关参数(音高、持续时间等),并生成与现有乐器类似,或全新音色的乐音.
乐器音色模拟一个简单的方法是通过手绘幅频曲线对弦各次谐波振动进行加权,再通过一个表示演奏方式(如弹弦、拉弦等,或通过手绘)的时域包络即可模拟部分弦乐器(钢琴、双簧管等)的音色.本文设计了一种通过跟踪鼠标拖动路线初步确定频率曲线,并根据不同频率的声波在自由声场中的衰减(基于将声波分解为球谐函数叠加的思想)对曲线进行加权的弦乐音生成方法,例如见图5所示的模拟乐音钢琴.添加的时域包络为指数衰减的形式,对应琴弦的弹拨.也可通过高斯白噪声加一阶低通滤波器或二阶带通滤波器可模拟部分体乐器(如沙锤、军鼓等).该过程的模型可用于接下来的乐音试听、旋律添加乐器、伴奏和鼓点等操作,例如图6所示的模拟乐音沙锤,带通频率为1 500~2 000 Hz,衰减频率为16 Hz,18 000 Hz,阻带衰减为10 dB,时域包络为指数上升与指数衰减生成的模拟乐音既可表示大部分传统乐器,用少量参数即可模拟昂贵的专业乐器,也可生成全新的时域波形,营造截然不同的听音体验.本小节生成的模拟乐音将用于整个音乐训练与生成系统,随时听取音乐片段并进行后期处理.
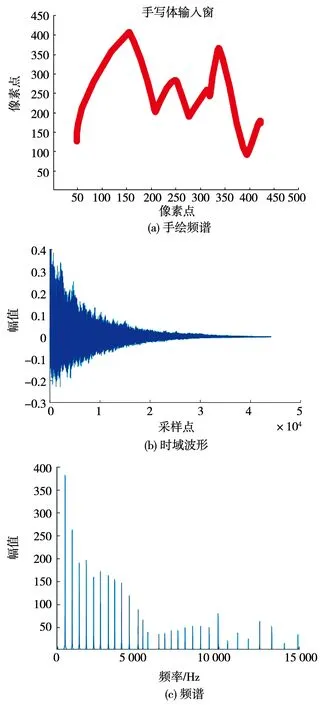
图5 模拟乐音钢琴特征分析

图6 模拟乐音沙锤特征分析
Fig.6 Characteristics analysis of the simulated sand hammer sound
5 音乐生成系统测试
本次通过哼唱《致爱丽丝》的部分小节作为训练数据,以《小星星》的前7个音符作为输入,经过迭代与人工删改后生成的谱表如图7所示.图8是上述乐谱添加模拟乐音后的时域波形图,动态上升了18,速度不变,音符丰富度上升1,虽然代价函数得分上升了12.63%,但仍在设置的门限范围内.该音频已具备一定艺术性,与《小星星》的听感完全不同.图9是上述乐谱基于乐谱二次折叠参数添加伴奏与鼓点后的时域波形图,相较于上述音频更加悦耳动听.

图7 一次生成测试的乐谱可视化结果

图8 乐谱添加模拟乐音后的时域波形
Fig.8 Time-domain waveform after adding simulated instrument to the music score

图9 乐谱添加伴奏与鼓点后的时域波形
Fig.9 Time-domain waveform after adding accompaniment and drums to the music score
与传统组合优化问题不同,由于生成的音乐片段具有一定艺术性,客观评价指标只能作为音乐生成的指导,客观评价指标得分高并不代表音乐片段悦耳动听,因此不能完全使用客观评价指标对生成结果进行评价,主观听感应作为音乐片段好坏的主要评价标准.通过对近年来提出音乐生成方法所提供的部分片段进行试听比较[13-21],得益于生成阶段的人机交互,本文提供的方法所生成片段更为动听,此外训练与生成过程也更为直观新颖,便于操作.
本系统可以从易获得的时域音频文件出发,通过较少的操作和较短的时间获得具有艺术感的音乐片段,能够直观地体验音乐的创作过程,利于充分调动音乐爱好者,特别是青少年的对音乐的热情,并能够通过预先设定的参数与乐器选择,进一步丰富音乐片段.但每次生成的持续时间较短,一般为4~10 s.
6 结 论
传统的作曲由于需要大量乐理知识与听音经验,普通的音乐爱好者很难参与其中.本文所述方法克服了传统作曲门槛过高、可重复工作量大等缺点,以及难以获得大量专业乐器音色的缺陷,提供了一种基于变邻域搜索与掩蔽效应的音乐生成方法,即让普通的音乐爱好者也能参与到作曲中,同时也能通过人机交互的方式充分调动音乐爱好者,尤其是青少年对音乐的积极性,并使其投入其中.此外,基于频域幅值与时域包络的乐音模拟算法也克服了大量乐器难以获得的缺陷,反之也可为乐器设计与校准提供参考.