APOS理论探索的反思与超越
摘 要 在APOS理论引介到我国之后的十几年里,我国的数学教育研究者开展了大量的实证研究、应用研究与评价研究。当前研究存在着一些对APOS理论的错误认识,比如:将APOS理论理解为一个线性的心理结构;将APOS理论定位为一种代数学习理论;认为APOS理论只能服务于数学概念的学习。走出认识误区,才能真正实现APOS理论的超越。一方面,APOS理论提供了学习新知的三种方式;另一方面,提供了划分数学问题解决学习阶段的依据。
关键词 APOS理论 概念学习 数学问题解决
APOS理论是美国学者杜宾斯基(Ed Dubinsky,1993)等人提出的一种建构主义的数学学习理论,讨论了数学学习的心理阶段或结构,即操作、过程、对象和图式[1]。在APOS理论引介到我国之后的十几年里,我国的数学教育研究者开展了大量的实证研究、应用研究与评价研究。一些研究定势使得基于APOS理论的数学学习研究陷入了瓶颈期,我们不得不放慢脚步,以摆脱当前“广而不深”“一叶障目”的研究局面。
一、APOS理论的本质认识与功能定位
APOS理论本质上讨论的是数学学习的心理结构与心理机制的问题。已有研究对这两个概念的混淆不利于学习者区分数学的阶段与方法。斯滕格(Stenger et al., 2008)等人对这两个概念进行了区分,指出“心理结构是个体用于理解数学情境的相对稳定的结构,而心理机制是个体头脑中形成这一结构的方法”[2]。这也就是说,心理结构是一种静态的结构,心理机制是一个动态的过程,心理机制使得个体从一种心理结构向另一种心理结构的转化成为可能。
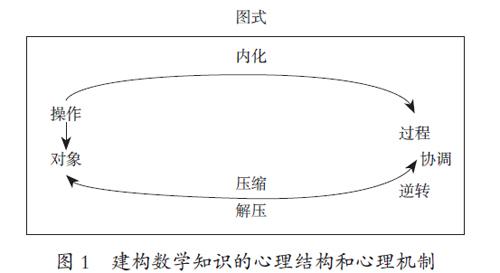
更为具体地,杜宾斯基等人用操作、过程、对象和图式来表示数学学习中的心理结构。对某一数学对象实施操作,这种操作经过内化成为过程,过程可以被压缩为一个完整的对象,整个系统成为图式的一部分,当个体运用图式去解决问题而不需要反思图式中的元素和关系时,则说明图式经过了主位化,主位化是个体有意识地将图式用于问题解决中的机制[3]。上述内化、压缩和主位化等方法就是贯穿于数学学习的始终的心理机制。此外,协调、逆转、解压等也是促进各种心理结构形成的心理
机制。
相应地,心理结构与心理机制的本质差异使得APOS理论可以从两个方面进行功能定位。首先,APOS理论具有诊断功能。它能够调查个体对数学概念的理解并描述个体的思维发展情况[1]。这一功能中,APOS理论作为一个分析工具,用于诊断学习者是否形成了某一心理结构,诊断的结果为学生数学学习的评价与行为纠正等提供了参考。其次,APOS理论具有解释功能。心理机制能够解释个体的数学知识是如何建构的[4]。这一功能中,APOS理论作为一个理论基础,对数学教学进行指导,或为进一步的应用研究提供依据。
二、APOS理论的反思
1.操作、过程、对象、图式并不是一个线性的结构
APOS理论的心理结构常被解读为从低层次到高层次的线性结构。事实上,数学学习的心理结构在心理机制的作用下形成了一个环形的结构(如图1所示),并且环形结构中的每一个要素间的联系不都是单向的。操作是一种直接进行的外部转换,每一步转换在外在的引导下精确地表示,既不能主观臆断,也不能随意跳过。过程不同于操作,虽然也是在执行转换,但是并不需要经过每一步。随着操作步骤的重复和对操作过程的反思,个体从依靠外在的提示转向依靠内部调控。内化使得这一心理变化成为可能。只有当个体尝试对过程进行压缩时,才有可能将一个动态的结构转化为可以应用的静态结构;只有当个体意识到过程可以作为一个整体时,才能形成对象。当然也存在这样一种情况:简单的操作或是达到高度自动化的操作,可以直接形成对象。
值得注意的是,一旦过程被压缩成心理对象,它还可以在需要引发的时候解压为潜在的过程。也就是说,经过解压机制,个体还能将对象还原为先前的过程。协调是基于多个过程建构新的对象所必不可少的心理机制,两个对象在分别解压为先前的过程后,相互协调并重新被压缩为一个新的对象,如复合函数概念的形成。逆转是建构新对象的另一心理机制。某一过程在逆转机制的作用下所形成的新过程,将被重新压缩为新的对象,如反函数概念的形成。操作、过程、对象三者之间的互动可以促成图式的形成,一旦图式作为连续结构的集合体被建构起来,并且集合体中各个结构的联系被建立起来时,这个图式就能被转化为一个稳定的结构或者可以同化其它图式的动态结构,也就是认知结构的重组。
2.APOS理论不只是一种代数学习理论
杜宾斯基在系统论述APOS理论时,选择了线性代数、统计和微积分作为具体的例证,但这并不意味着该理论不适用于几何知识的学习。与代数知识不同,几何知识的学习是由具体到抽象的过程,几何图形或几何体是由生活中的具体实物抽象而来。具体来说,操作这一心理结构在几何学习中表现为能够借助外在的提示,找到或列举出与某一实物类型相同的其它实物;在进一步的学习中,逐渐表现出摆脱提示,并能够从已有的例子出发,类比出同类的其它实物即为过程;而能够总结出这一类事物所具有的本质特征,才能够形成对这一类实物的完整认识,并尝试概括出具体概念以及抽象出代表这一类实物的几何图形或几何体。类似的过程在高等几何中也是存在的,根据图形与空间的关系,可以对几何图式的发展进行描述,如从欧氏几何关注的图形的表征与图形的性质,到变换系统的引入,再到变换群的引入[3]。因此,APOS理论也是适用于几何学习的理论。
3.APOS理论不只服务于数学概念的学习
一般认为,APOS理论是数学概念学习理论,但并不等同于APOS理论只服务于数学概念的学习。静态的概念学习最终会向高阶思维水平发展,其达成的学习结果也不再是陈述性的知识。杜宾斯基从建构主义的视角分析了数学学习的过程,他认为个体的数学学习是在经过思维的操作、过程、对象之后,将它们组合成图式[3]。操作即感知到外部刺激,并对刺激进行转换。这种对不同刺激作出不同反应的能力也就是加涅智慧技能层级论中的“辨别”。接下来,在“辨别”基础之上形成的“概念”,也是学习者通过操作达成的学习结果。因此,一般运用APOS理论进行的所谓的概念教学,其达成的学习结果已不仅仅是“概念”,其教学内容已涉及对“概念”的进一步理解和运用,它可以达成更高层次的智慧技能。过程和对象这两个心理结构的相同之处在于形成了以“概念”为前提的“规则”,不同之处在于过程强调一种过程模式的建构,相当于“规则”的自动化;对象强调将过程作为一个整体进行转换或运算,是指“规则”的迁移与运用。由过程向对象的转化构成数学思维的一个基本形式[5]。包括操作、过程、對象在内的整个认知系统即为图式,不同图式的整合和精致将伴随简单“规则”的复杂组合。这一阶段所形成知识的综合图式将被纳入自身的认知结构中,与已有的知识建立新的实质性联系[6]。因此,图式是有助于达成加涅智慧层级论中的“高级规则”的心理结构,是学生数学问题解决学习的前提条件。
三、APOS理论的超越
不得不承认的是,一直以来对APOS理论的一些误解使得研究者和一线工作者对这一理论的认识是片面的、甚至是错误的。走出APOS理论的认识误区是实现理论超越的必由之路。
1.APOS理论提供了学习新知的三种方式
APOS理论有助于理解数学学习的本质并提高数学学习的科学性。该理论提供了学习新知的三种方式,这三种方式遵循了不同心理结构的发生发展的顺序。
(1)操作—过程—对象
“操作—过程—对象”是三种学习新知的方式中最为基础的一种,围绕这一种方式开展的应用研究也是最为普遍的。内化和压缩两种心理机制分别实现了这一学习方式中的两次转化,即“操作—过程”的转化和“过程—对象”的转化。以函数为例,当学习者从不同给定点函数值的重复计算,发展为在大脑中形成一种“对应关系”的过程模式时,也就是将一种外部刺激内化为一种过程模式,完成了从“操作”到“过程”的转化;当学习者进一步将这一种“对应关系”以整体的形式用于运算,并能够对函数的性质作出判断时,则是将这一“过程”压缩为一个“对象”[7]。“操作”“过程”和“对象”是数学学习中的三个基本要素,当这三个要素以其它的顺序或形式进行转化时,还需要其它的心理机制作支撑。解压、协调、逆转的心理机制提供了学习新知的另外两种方式,这也是容易被研究者忽视的两种方式:“两对象—两过程—相互协调的过程—新对象”和“对象—过程—逆转后的过程—新对象”。
(2)两对象—两过程—相互协调的过程—新对象
某些新的对象的形成需要以两个甚至多个静态的对象为学习基础,这一新的对象的形成不能简单理解为先前多个对象的叠加,而是需要将先前的对象还原为可操作的过程,并且使这些过程相互协调地整合在一起,再次压缩为一个整体,形成一个新的对象。同时,我们会发现,组合的顺序也会影响新的对象的形成,如复合函数f ( g (x))与g ( f (x))虽然都是以函数f (x)、g (x)为基础,却形成了两个不同的函数对象。在形成这两个复合函数之前,我们对函数f (x)、g (x)的认识需要重新回归到“在定义域内给定任意一个x值都有一个相应的f (x)值与之对应”的动态过程中,这一动态过程影响着形成新对象定义域的过程。在认清f (x)的定义域为
{x丨x∈A},g (x)的定义域为{x丨x∈B}的基础上,生成复合函数f ( g (x))的定义域{x丨g (x)∈A∩x∈B},
以及g ( f (x))的定义域{x丨x∈A∩f (x)∈B}的过程,用到的就是心理机制中的协调,这一过程还将被压缩为新的整体,实现个体对这一对象的完整认识。
(3)对象—过程—逆转后的过程—新对象
还有一类对象不能独立于另一对象单独存在,而是与另一对象成对出现。这类对象的特点是不能脱离另一对象的形成过程实施教学。如“相反数”这一对象的形成首先要将个体对“数”的整体认识还原为一个过程——正数就是数轴上从原点出发向右移动若干单位的位置所表示的量,零是数轴上原点位置上表示的量,负数是数轴上从原点出发向左移动若干单位的位置所表示的量;“相反数”这一对象则是在上述过程的逆转机制中生成的,即个体需要在数轴上表示出表示相反意义的量,再将这一过程压缩为具体的对象。又如,“对顶角”这一概念的形成也要将个体对“角”的整体认识还原为一个过程——从一个端点出发引出两条射线,“对顶角”则是反向延长这两条射线所形成的,同样也用到了逆转的心理机制。类似地,“平方”与“平方根”,“函数”与“反函数”等数学对象的形成也是如此。
不难看出,本文所论述的学习新知的三种方式共同组成了数学学习的环形结构。
2.APOS理论提供了划分数学问题解决学习阶段的依据
尽管国内外学者和研究机构对问题解决的界定是多样的[8],数学问题的形式是丰富的,而且每一个问题的具体解决过程不同,但从整体上考察这些问题解决的过程,它们却是有规律的[9]。APOS理论中的图式形成的三个阶段为数学问题解决学习的阶段划分提供了理论依据,明确每一阶段的学习任务对落实数学问题解决的教学计划具有重要意义。
(1)数学问题解决学习的准备阶段
尚处于准备阶段的学习者,已经习得解决数学问题所需要的概念和规则,却没有形成或者只形成了部分可操作的对象。其解题过程常表现得相对具体,需要借助具体的实物来表征问题中的数量关系或位置关系,有时还会把一些无关的条件考虑到问题中。进入准备阶段的学习者的学习任务是有选择地将这些概念和规则用于组合。加涅将这种简单规则的復杂组合称为高级规则,并指出创造这种复杂规则或者高级规则的目的是为了解决一个或一类实际问题[10]。学习者对所需要的概念和规则进行的不同选择决定了所形成的高级规则的多样性。这一阶段的特点表现为每一个形成的高级规则都是一次认知结构的重组。与此同时,形成了多个处于离散状态的心理结构。
(2)数学问题解决学习的结构化阶段
学习者已经习得多个高级规则,却未能形成一个结构化的操作对象,其解题过程表现得相对抽象,如借助几何直观来表征问题中的数量关系和位置关系,解题图式的各个构成要素也在经历了准备阶段之后变得丰富起来,具备了进入结构化阶段的学习条件。在明确这些高级规则的区别与联系的基础之上,根据这些高级规则的特点和功能将其进行组合,是结构化阶段的学习任务。也就是说,高级规则可以组合成更为复杂的规则来解决问题,组合的目的是为了在运用图式解决问题时能够更加灵活、有效地进行迁移。这一阶段包括两个甚至多个高级规则的整合,以及将某一高级规则整合到另一个高级规则的情况。这一阶段的整合是认知结构的再一次重组。与此同时,上一阶段处于离散状态的图式变得连续起来。图式的连续性标志着学习者具备了将图式作为一个整体应用于各种问题情境的条件。
(3)数学问题解决学习的迁移阶段
对于将多个可操作的对象联系起来,却不能将其作为一个整体在不同的问题情境中自由迁移的学习者来说,迁移阶段是必须经历的学习阶段。图式拓展的程度不是衡量图式是否完善的全部标准,图式的完善还取决于情境化和条件化的发展。迁移的概括性理论认为,两个学习活动之间存在共同要素只是产生迁移的前提,产生迁移的关键则是学习者从两种学习活动中概括出它们的共同原理[11]。这也就是说,图式的迁移取决于新的问题情境能否概括出与已有图式相同的原理。因此,迁移阶段的具体任务包括判断新问题是否属于某一图式的应用范围,明确这一图式在不同问题情境中的限制條件,能够在不同情境中将这一图式合理地迁移和运用。这一阶段形成的图式是高级规则与具体情境整合的结果,学习者在具体情境中形成对图式内部各组成要素间相互关系的深入理解。与此同时,也呈现出丰富性、特殊性和发展性的特点[7]。唯有经历了迁移阶段的学习,才能达到更为抽象的思维水平,更加灵活地选择和运用已经形成的图式,才能在面对更为复杂的情境时摆脱无关信息的干扰。
一番思考后发现,APOS理论的贡献并不局限于给出了数学学习的一般规律,还在于为图式水平划分提供了依据,为测验材料的编制提供了参考。至此,APOS理论在其“分析学生思维”“关注思维发展走向”的功能定位上将发挥更大的作用。教育研究的繁荣使得每一个时代都在孕育着新的理论。有的理论经得起时间的沉淀,成为教育研究史上的经典之作;有的理论虽然留下了浓墨重彩的一笔,却终究被取代。阻碍理论生命延续的不只是自身的缺陷,还在于教育研究者能否走出认识的误区,深入挖掘理论的本质,并赋予理论新的生命。
参考文献
[1] Lerman S. Encyclopedia of Mathematics Education[M]. Dordrecht :
Springer Netherlands, 2014.
[2] Stenger C, Weller K, Arnon I, et al. A search for a constructivist approach for understanding the uncountable set P (N)[J]. Revista latinoamericana de investigación en matemática educativa, 2008(01).
[3] Arnon I, Cottrill J, Dubinsky E, et al. APOS theory: A framework for research and curriculum development in mathematics education[M]. New York : Springer Science & Business Media, 2014.
[4] Inglis M. Review of APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education [J]. International Journal of Research in Undergraduate Mathematics Education, 2015(03).
[5]濮安山,史宁中.从APOS 理论看高中生对函数概念的理解[J]. 数学教育学报,2007(02).
[6]吴华,周鸣.GeoGebra环境下基于APOS理论的数学概念教学研究——以导数概念为例[J]. 数学教育学报,2013(02).
[7]乔连全. APOS:一种建构主义的数学学习理论[J]. 全球教育展望,2001(03).
[8]邓鹏.对“问题解决”的反思[J]. 数学教育学报,2002(02).
[9]何小亚.解决数学问题的心理过程分析[J]. 数学教育学报,2004(03).
[10]加涅.教学设计原理[M]. 皮连生,等,译.上海:华东师范大学出版社,1999.
[11]李淑文.在数学问题解决中哪些知识能促进迁移的产生[J]. 数学教育学报,2000(04).
[作者:马晓丹(1989-),女,天津人,北京教育学院初等教育学院,讲师,博士。]
【责任编辑 杨 子】

