关联学习:关联关系挖掘新视角
钱宇华 张明星 成红红
(山西大学大数据科学与产业研究院 太原 030006) (计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006) (山西大学计算机与信息技术学院 太原 030006)
探索未知事物的关联关系有助于理解人类关联认知机理.美国加州大学伯克利分校Speed[1]在《Science》杂志上发表论文称,从庞大的数据集中发现数据之间潜在的关系十分重要.梁吉业等人[2]在2016年指出大数据相关分析是探寻与发现事物内在规律的重要“导航”工具,自然也是大数据分析与挖掘的关键科学问题.钱宇华等人[3]在2015年指出关联性学习的概念,并指出关联学习是大数据理论与基础的重要研究内容之一.
早在19世纪80年代研究者开始展开关于关联关系挖掘的研究,Galton[4]在研究人类身高遗传问题时首次提出了相关的概念.Pearson[5]于1988年提出Pearson相关系数,用于刻画最简单的线性相关关系,此后经过一个多世纪的发展,线性相关系数有了较为完整的理论基础和广泛的应用领域.1959年Renyi[6]给出了关联依赖度量需满足的公理化性质,此后研究者基于此公理化要求提出多种形式的关联度量.2011年《Science》杂志上Reshef等人[7]通过网格划分估计概率估计互信息,提出能识别线性和非线性共存的复杂关系度量——最大信息系数(maximal information coefficient, MIC).1936年典型相关分析[8](canonical correlation analysis, CCA)被提出用于刻画变量组间的线性关系,通过同时寻找2个随机向量的线性投影确定相关关系.CCA只能识别简单的线性关系,对于复杂的非线性关系,研究者们分别提出了核典型相关分析[9](kernel canonical correlation analysis, KCCA)尝试通过核映射到希尔伯特空间去识别原始空间中的非线性关系.深度典型相关分析[10](deep canonical correlation analysis, DCCA),是通过深度神经网络学习复杂非线性映射,以期得到变换后的线性相关关系.
而在大数据时代,数据通常以多模态形式呈现,多模态对象之间可能存在关联性,并且研究对象具有特定的语义,想要刻画对象之间复杂的非线性关系,通过构造方式的关联关系发现方法往往不能遍历所有的关系空间,从而无法合理地刻画关联关系.而且在人类认知事物的过程中,对已知事物的了解和学习可以对未知事物起到预测和借鉴的作用.回顾已有的关联关系挖掘方法,都是基于某种假定构造关联关系度量,对未知数据缺少借鉴作用.因此,本文尝试采用学习方式来刻画事物之间的关系,学习一种具有关联判定能力的关联关系学习模型.目前的关联性分析任务主要关注2个变量(向量)之间的相互依赖关系,并且只是对经验数据的统计分析,而学习2个对象之间关联关系的模型尚未报道,从学习角度探索2个对象之间的关联关系并对未知数据有判别能力的关联学习模型值得尝试.
类似机器学习中监督学习任务的研究思路,本文首先提出关联学习的输入空间、特征空间、输出空间以及假设空间的定义,讨论了关联学习的联合概率分布和形式化定义,根据关联学习的概念,设计了关联学习模型以及模型评估方法;依据形式化定义构建了二类关联图像数据集(two class associated image data sets, TAID),利用卷积神经网络提取关联特征,然后分别用softmax函数和K近邻算法训练关联判别器,提出3种关联判别器模型:关联图像卷积神经网络模型(associated image convolutional neural network discriminator, AICNN)、关联图像LeNet模型(associated image LeNet discriminator,AILeNet)和关联图像K近邻模型(associated imageK-nearest neighbor discriminator, AIKNN),并将3种判别器模型应用于TAID数据集进行关联学习;最后总结了关联判别器的可行性并指出关联学习问题未来的研究方向.
1 关联学习(association learning)
关联学习研究实例对之间的关联关系,从给定的实例对中学习一个关联判别模型,使其能对新的输入实例对进行关联关系判别.
1.1 关联学习基本概念
关联学习任务类似监督学习[11](supervised learning)任务,参考监督学习的相关概念,本文首先给出关联学习问题中的一些基本概念:
1) 输入空间U.输入变量记作U=X,Y,输入变量的取值u=x,y,x∈X,y∈Y,u=x,y称为实例对,x∈X,y∈Y分别为对应空间中的元素(实例).需要注意的是实例对u=x,y中的元素可以互换位置,也可能取同一空间中的元素,也即实例对有3种可能形式:u=x,x;u=x,y;u=y,y.
2) 特征空间.输入实例对u的特征向量记作u=x,y,其中x∈Rp,y∈Rq,p和q分别为实例空间的维度.x和y的特征空间维度可以不同.
3) 输出空间A.输出变量记作A,可以是连续型和离散型变量.a是输出变量的具体取值,表示实例对的关联关系.
4) 联合概率分布.假设关联学习数据集具有联合分布,即输入与输出变量U和A服从联合概率分布P(U,A),表示关联分布函数或关联密度函数.在关联学习过程中,假定此联合概率分布存在,但对于学习系统来说,联合概率分布的具体定义和形式是未知的,约定训练数据与测试数据依联合概率分布P(U,A)独立同分布产生的.
5) 假设空间F.假设空间定义为关联判别映射的集合F={f|A=f(U)},f是由一个参数向量决定的函数族:F={f|A=fθ(U),θ∈{〈Rp,Rq}},参数向量θ取值于所研究对象所在的欧氏空间Rp,Rq,称为参数空间.关联学习的目的在于从假设空间中找到最好的关联学习判别模型.
给定关联学习问题的相关概念,下面给出关联学习问题的形式化定义:
定义1.给定数据集T={(u1,a1),(u2,a2),…,(uN,aN)},其中ui=xi,yi是输入空间中的观测值,xi∈Rp,,yi∈Rq,ai是输出空间中的观测值,由输入空间到输出空间的映射过程称为关联学习.根据输出空间的取值类型不同,关联学习存在如下2种学习模式:
1) 如果A是连续型随机变量,即A∈R,a为关联强度得分,得到的映射称为关联度量.具体地:从给定数据集中估计一个关联度量m:U→A,这个过程称为关联强度推断.在实际问题中,m(U)∈[0,1],0表示随机变量X与Y的关联强度最弱,说明两者之间无关联关系;1表示随机变量X与Y的关联强度最强,说明两者之间存在强相关关系.
2) 如果A是离散型随机变量,即A∈{a1,a2,…,an},ai∈Z,称为关联标签,学习到的映射称为关联判别器.具体地:从给定数据集中学习一个关联判别器f:U→A,这个过程称为关联判别器学习.以简单的2类实例对为例,对应的输出空间为A∈{-1,0,1},-1表示实例对的关联标签为负关联,0表示实例对的关联标签为无关联,1表示实例对的关联标签正关联.
本文主要关注2类实例对的关联判别器学习问题,不混淆情况下,文中统称为关联学习.如图1所示:当给定一个训练数据集T={(u1,a1),(u2,a2),…,(uN,aN)},ui=xi,yi为输入实例对,分别用不同颜色的三角形和圆形表示,通过关联学习系统获得关联判别器,在关联判别阶段,当新输入1个uN+1=xN+1,yN+1实例对时,利用学习到的关联判别器给出输入实例uN+1的关联标签aN+1.
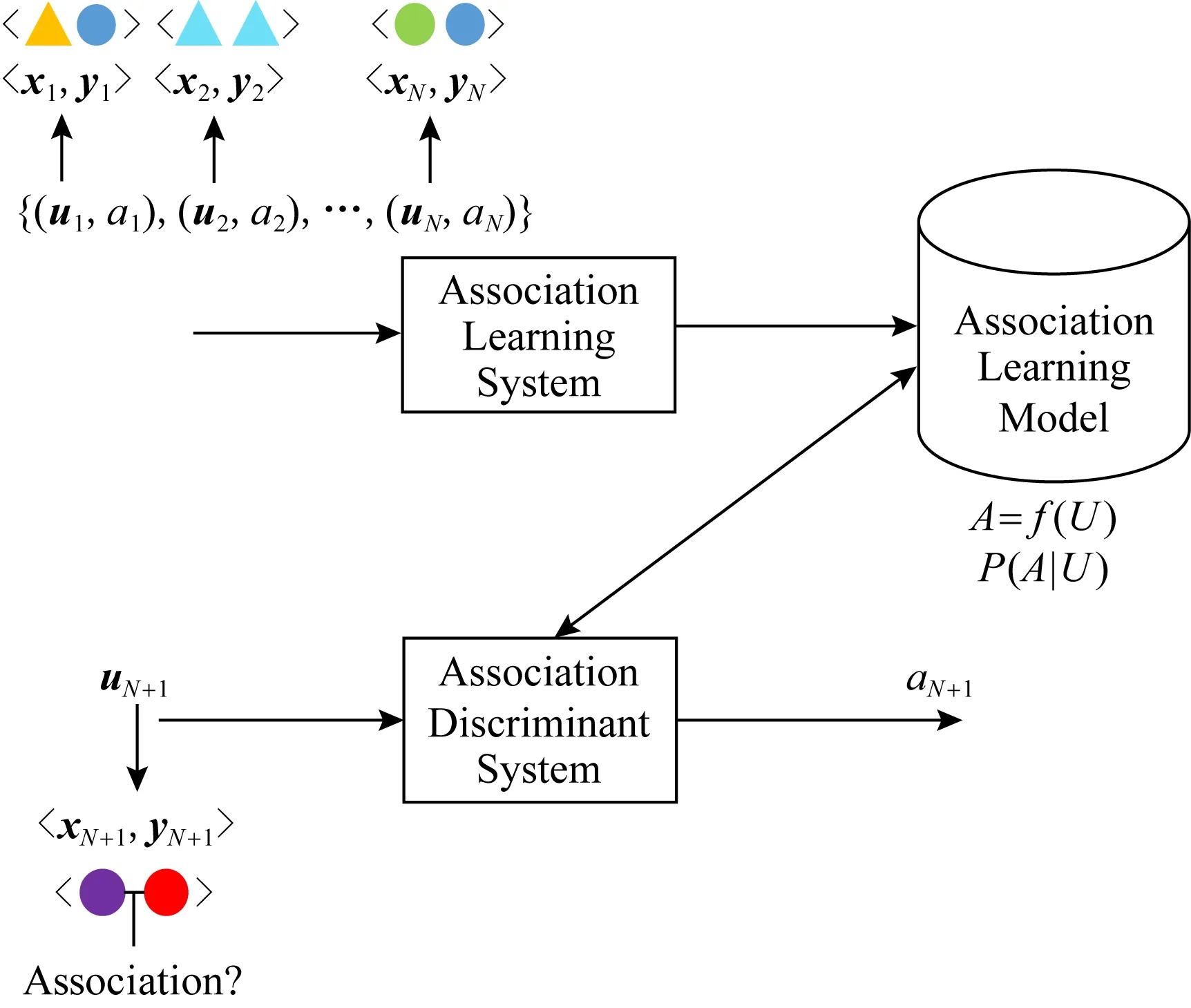
Fig. 1 Association learning schematic diagram图1 关联学习示意图
1.2 关联学习准则
给定关联学习的假设空间,需要考虑从假设空间中选择最优模型的准则.
类似统计机器学习中选择模型的标准,关联学习模型也可以通过损失函数衡量一次模型预测的好坏,通过风险函数度量平均意义下模型预测的好坏.
1) 损失函数.衡量关联判别器输出和真实值之间的不一致程度的度量称为损失函数(loss function).从假设空间F中选择一个关联判别器,对于给定的实例对U,判别器给出的输出为f(U),则损失函数记作L(f(U),A).根据不同的关联判别模型,L可以设置不同的形式.
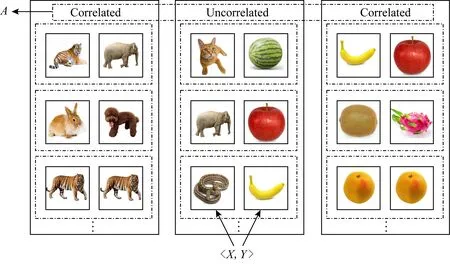
Fig. 2 Construct association learning data sets图2 关联学习数据集构建
2) 风险函数.模型的输入、输出(U,A)是随机变量,遵循联合分布P(U,A),模型f(U)关于联合分布P(U,A)的平均意义下的损失称为风险函数或期望损失记作Rexp,
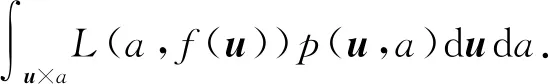
真实环境中关联学习的联合分布是未知的,风险函数中的期望值无法确定.实际中可采用经验风险代替.
3) 经验风险.对于上述给定的训练数据集T={(u1,a1),(u2,a2),…,(uN,aN)},模型f(U)关于训练数据集的平均损失称为经验风险或经验损失,记作Remp(f):
期望风险Rexp(f)是模型关于联合分布的期望损失,经验损失Remp(f)是模型关于训练样本集的平均损失,根据大数定律,当样本容量N趋于无穷时,经验损失Remp(f)趋于期望损失Rexp(f).经验损失最小化的策略认为,经验损失最小的模型就是最优模型.根据这一策略,按照经验损失最小化求最优化模型就是求解最优化问题:
其中F为假设空间.
本节给出关联学习问题中的一些基本概念和模型选择准则,接下来将对关联学习的具体模型进行分析.
2 图像间关联学习模型
在人类认知事物的过程中,通常通过建立2个对象之间的联系来分析记忆事物,复杂的关联认知过程存在于人类的大脑神经元中,本文尝试模拟人类联想认知的思维过程和行为方式.在图像识别方面,计算机对图像的识别能力甚至已经超过了人类,因此首先研究图像对之间的关联关系识别过程.
2.1 图像关联数据集构造
本文首次提出从学习的角度挖掘关联关系,需要将生活中的关联问题抽象化并构造符合关联学习定义的数据集.以动物和水果的识别过程为例,人们会认为2种动物或者2种水果的关联性比1种动物和1种水果的强,这种关联关系的学习过程在大脑中已经形成判断标准,但不能抽象地表示出来.
以动物和水果之间关系识别为例,同是2种动物的称为动物类,输入为动物-动物实例对,标记关联标签为-1;同是2种水果的称为水果类,输入为水果-水果实例对,对应的关联标签为1;1种动物和1种水果的实例对称为无关类,输入为动物-水果或水果-动物实例对相关的关联标签为0.-1和1都代表实例对之间是强相关的,为了区分动物类和水果类采用不同的类别标记,这2种标记是可以互换的.数据集的构造如图2所示:
2.2 图像关联数据特征提取
深度学习在图像识别方面有着非常领先的优势,本文采用深度学习中的卷积神经网络提取关联特征.LeCun[12]在1998年提出LeNet,用于解决手写数字识别任务.之后,CNN的最基本的架构就确定为:卷积层、池化层、全连接层.深度网络现在也已被广泛地应用于对数据进行表征的学习中,例如深度玻尔兹曼机[13]、深度自动编码器[14]和深度非线性前馈网络[15],它们在学习数据视图的表示方面取得了很大的成功.2006年后,随着深度学习理论的完善,尤其是逐层学习和参数微调(fine-tuning)技术的出现[16],卷积神经网络开始快速发展,在结构上不断加深,各类学习和优化理论得到引入[17].自2012年的AlexNet[18]开始,各类卷积神经网络多次成为ImageNet大规模视觉识别竞赛(ImageNet large scale visual recognition challenge, ILSVRC)[19]的优胜算法,包括2014年的ZFNet[20]和2015年的ResNet[21],以及具有很强拓展性的VGGNet[22],其有很强的泛化能力、稳定的卷积特征和较好的表达能力.本文借鉴上述的一些经典神经网络提取关联数据集的特征.具体的提取方法及参数设置在实验部分详细介绍.
2.3 关联判别器设计
采用卷积神经网络得到关联数据集的特征,采用ReLU(rectified linear unit)函数f(x)=max(0,x)作为关联判别器的激活函数,如图3所示:
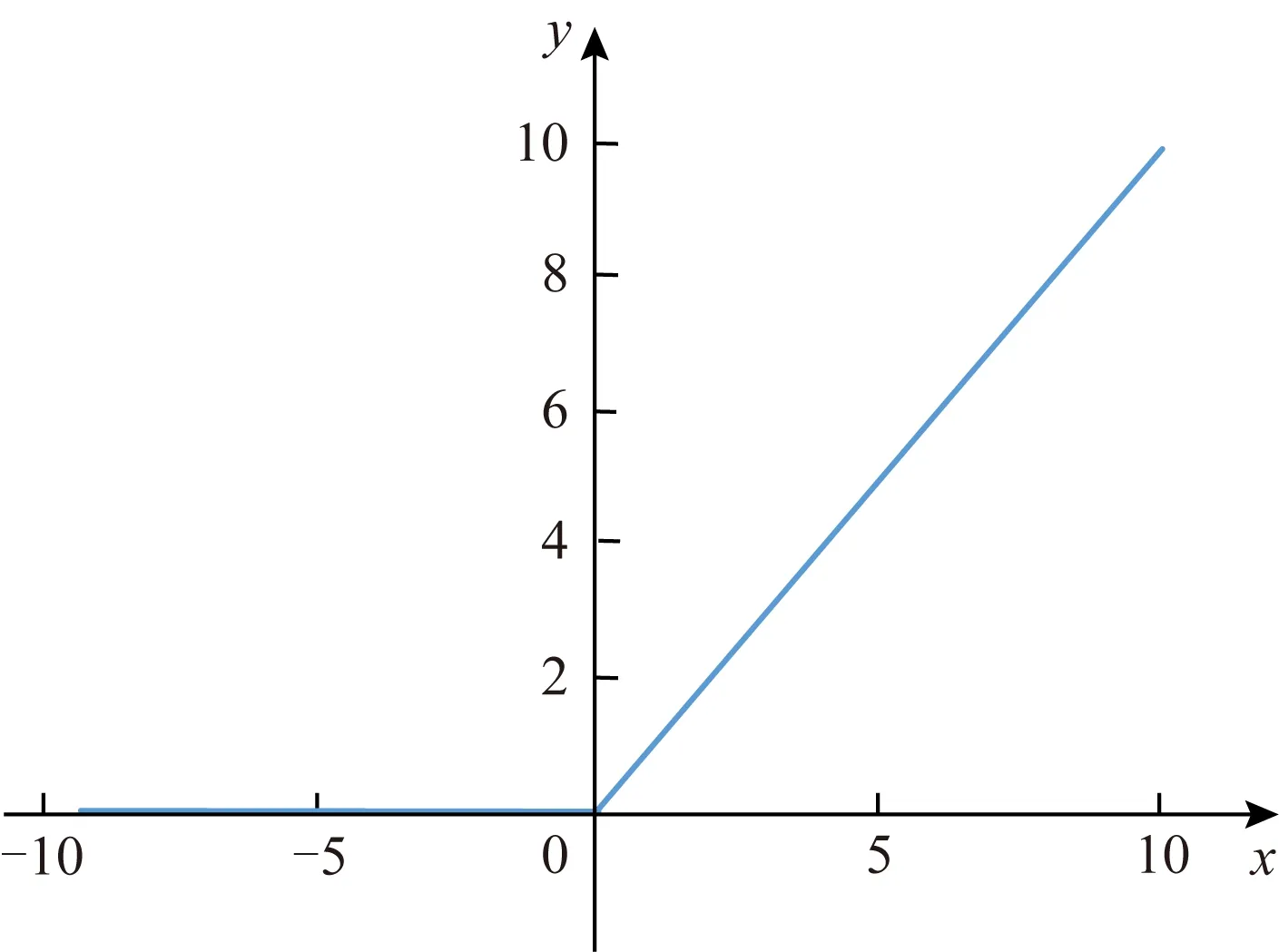
Fig. 3 ReLU activation function图3 ReLU激活函数
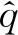
(1)
(2)
(3)
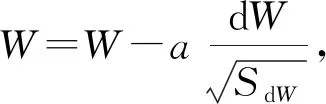
Adam优化算法基本思想是将动量梯度下降和RMSprop结合.基本步骤:
1) 初始化.vdW=0,SdW=0,vdb=0,Sdb=0.
2) 计算微分dW,db.
3) 计算动量指数加权平均数.
4) RMSprop更新,需要计算修正偏差.
2.4 关联判别器评估

其中N′是测试样本容量.
本文采用0-1损失函数:L(A,f(U))=f(x),f(x)={0,1|当A=f(U)时为0,当A≠f(U)时为1}进行模型评估,损失函数值越小,模型就越好.具体实验模型评价指标为测试精度,记作val_acc,
其中N′是测试样本容量.
3 关联判别器应用
第1节和第2节设计了图像间关联学习的模型以及一些评价标准,现检验关联学习的理论框架在图像关联数据集上的应用.图4展示了关联学习应用的整体模型,以2类关联图像数据为例学习关联判别器的过程.
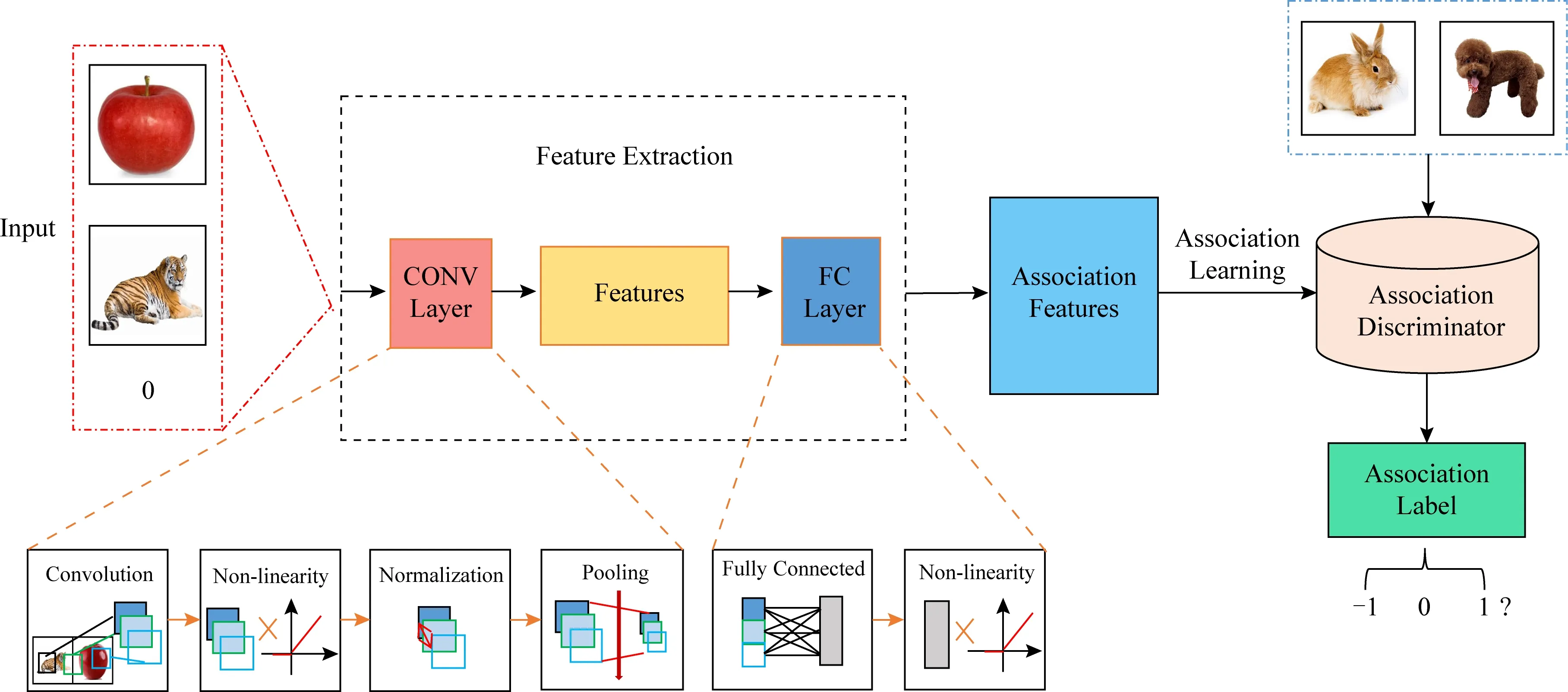
Fig. 4 Application of association learning图4 关联学习应用示意图
3.1 关联判别器应用数据集
如图2所示,构建2类关联图像数据集(TAID).具体地:分别选取100种不同的水果和100种不同的动物,其中任意挑选75种水果和75种动物,将这些水果和动物组合成150个对象,对象之间两两组合构成22 500个训练样本对,剩下25种水果和25种动物组合成50个对象,对象之间两两组合构成2 500个测试样本对(22500train-2500test),训练和测试对象种类没有重合,对于图片像素设置了3组不同的大小分别为64×64,128×128,256×256.
同样的方法分别找到150种不同的水果和150种不同的动物,其中任意挑选100种水果和100种动物,将这些水果和动物组合成200个对象,对象之间两两组合构成40 000个训练样本对,剩下50种水果和50种动物组合成100个对象,对象之间两两组合构成10 000个测试样本对(40000train-10000test).同样的方法分别找到200种不同的水果和200种不同的动物,其中任意挑选150种水果和150种动物,将这些水果和动物组合成300个对象,对象之间两两组合构成90 000个训练样本对,剩下50种水果和50种动物组合成100个对象,对象之间两两组合构成10 000个测试样本对(90000train-10000test),40000train-10000test和90000train-10000test数据集只设置了64×64大小像素的图像.
3.2 实验设置及结果展示
首先选用4种经典的卷积神经网络模型LeNet,AlexNet,ZFNet,ResNet,分别在TAID数据集设置的22500train-2500test,40000train-10000test,90000train-10000test的64×64维图像进行实验.
同时本文还提出了一个关联图像卷积神经网络模型(association image CNN, AICNN),图5所示为模型的结构,其中不同的颜色代表模型中所使用的网络层类型不同.用上述的数据集进行了实验,迭代次数都为40次.对于各个模型的关联判别精度做了一个统计,如表1所示,可以发现在本文提出的AICNN模型中3个数据集的关联判别精度都最高,其中90000train-10000test的数据集关联判别精度达到了0.821 7;对于其他模型实验判别精度的结果,40000train-10000test和90000train-10000test明显高于22500train-2500test的数据集.
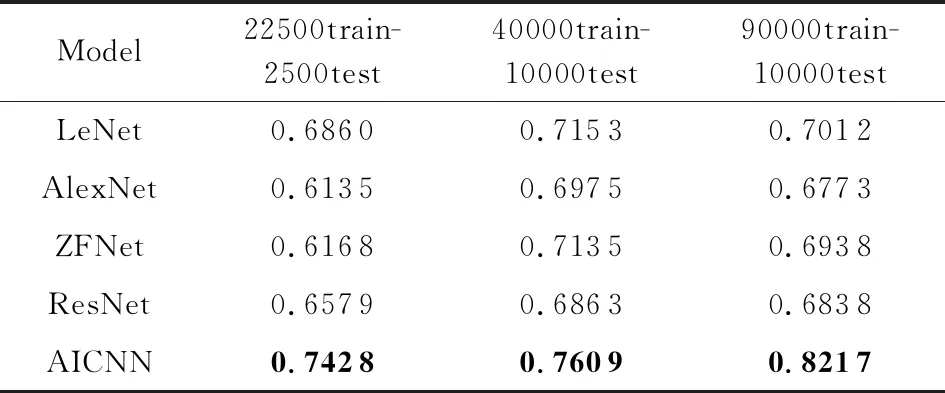
Table 1 Model Discriminant Accuracy表1 模型关联判别精度表
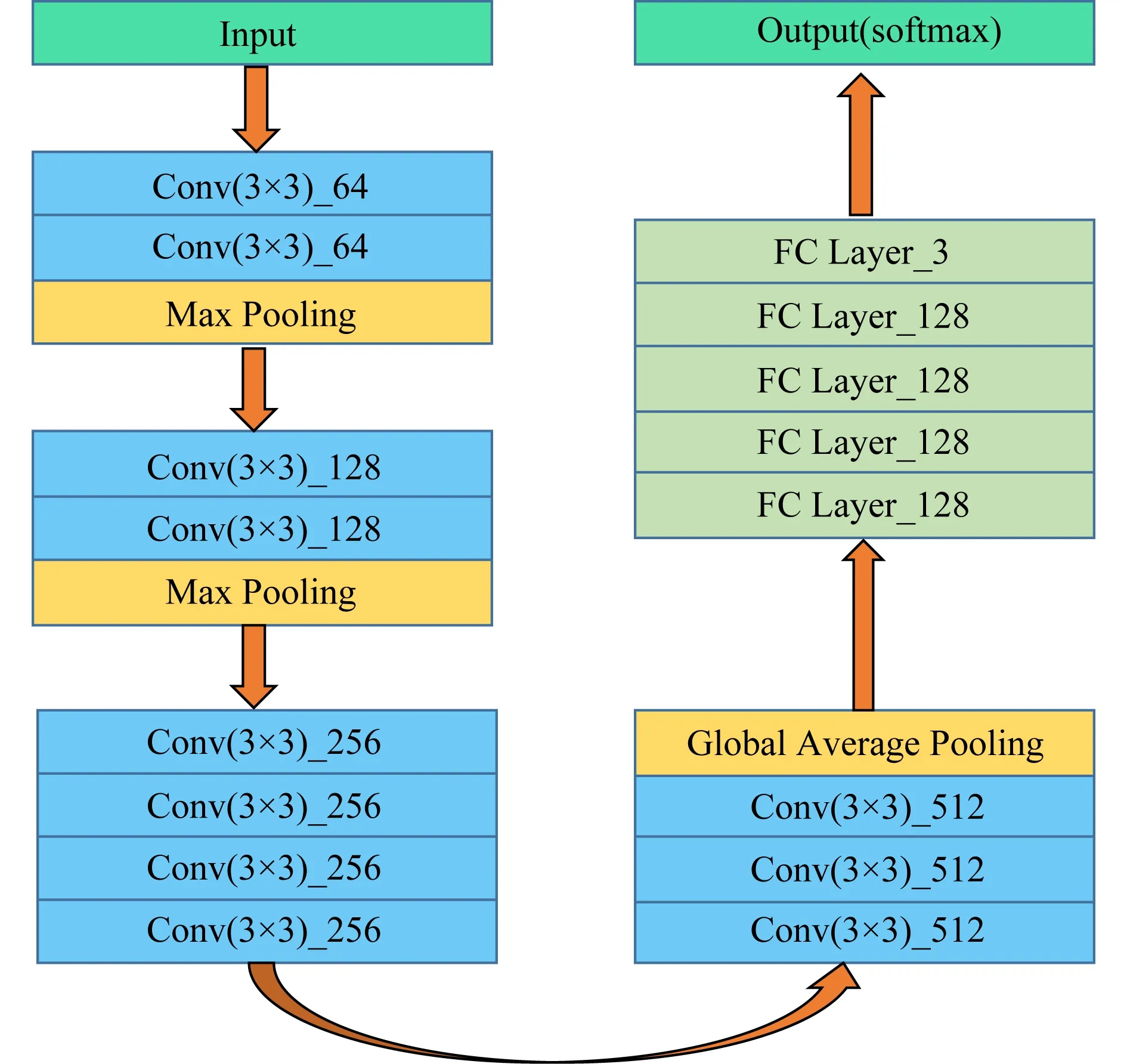
Fig. 5 AICNN model图5 AICNN模型
如图6所示,用AICNN模型在90000训练样本中随机选择22500,40000,62500,90000样本分别进行40次迭代训练,用相同的10000样本测试发现90000训练样本关联判别精度最高为第23次迭代的0.821 7,62500训练样本判别精度最高为第30次迭代的0.785 1,40000训练样本判别精度最高为第30次迭代的0.776 8,22500训练样本判别精度最高为第40次迭代的0.743 8.实验结果表明在训练样本增多的情况下,模型判别效果好并且达到最高测试精度的模型迭代次数少.
在22500train-2500test样本中,分别对64×64,128×128,256×256这3种不同像素的样本使用LeNet模型进行了实验,由于256×256像素样本经过AICNN模型11层卷积训练出现内存不足的问题,所以在LeNet模型的基础上对模型的卷积层进行了修改如图7所示,其中不同的颜色代表模型中所使用的网络层类型不同.对AILeNet网络的模型进行实验,结果如图8所示,在AILeNet模型实验中256×256像素样本迭代60次之后的判别精度最高到达了0.845 6.
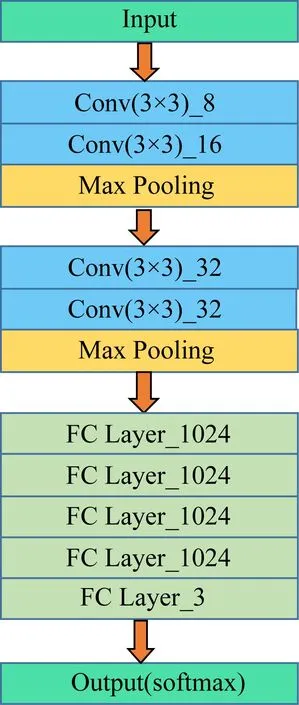
Fig. 7 AILeNet model图7 AILeNet模型
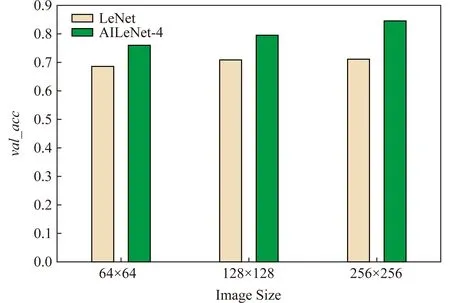
Fig. 8 Three different pixel samples test accuracy图8 3种不同像素样本测试精度
在对LeNet模型的改进过程中,我们分别进行了3层卷积、4层卷积、5层卷积的实验如图9所示,其中图7为4层卷积模型,3层卷积和5层卷积分别为减少和增加32个3×3的卷积,3层卷积关联判别精度为0.831 6,4层卷积关联判别精度为0.845 6,5层卷积关联判别精度为0.843 6,实验结果表明在图像像素大的情况下可以提供的关联特征较多,并且较少的卷积层数可以使关联判别器的判别精度变高.

Fig. 9 AILeNet test accuracy图9 AILeNet模型实验测试精度
从另外一个角度考虑,使用传统的机器学习K近邻算法,我们提出一个新的关联图像K近邻(asso-ciation image KNN, AIKNN)模型.首先将22500train-2500test样本中64×64,128×128,256×256这3种不同像素的样本图像使用VGG-19训练对训练和测试数据进行特征提取,降为1 000维向量;然后取K=9使用KNN算法进行关联判别器训练实验,结果如图10所示:256×256像素的数据集22500train-2500test测试精度为0.866 4. 2种角度的关联判别器模型得到的关联预测精度接近85%,说明从学习的角度挖掘关联关系的方法值得探索.

Fig. 10 AIKNN test accuracy图10 AIKNN模型实验测试精度
4 总结与展望
本文提出从学习的角度研究关联关系挖掘问题,尝试给出关联学习基本概念如输入空间、特征空间、输出空间及假设空间等,并给出关联学习的形式化定义,评估模型的损失函数和风险函数定义.根据关联学习的形式化定义以及模拟人类关联认知的思维过程,构建了简单的二类关联图像数据集(TAID),并用卷积神经网络对关联图像数据集进行特征提取,在此基础上用softmax函数和K近邻算法训练关联判别器,根据训练方法的不同,分别提出AICNN,AILeNet,AIKNN这3种关联判别模型.在测试阶段ALLeNet判别器的判别精度达到0.845 6,AIKNN判别器的判别精度达到0.866 4,实验结果初步验证了学习角度的关联关系挖掘的可行性.
关联关系挖掘是大数据基础理论研究中的重要内容之一,现有的关联关系挖掘多是基于统计学假定的关联强度估计,本文首次探索学习角度的关联学习模型,为相关领域的研究者提供了一种新的研究视角.在初次研究过程中,不管是关联学习理论基础的搭建、数据集构建还是关联判别模型的设计和评估函数的选择都存在不完善之处,虽然部分实验验证了关联学习的可行性,但是关于这个角度的关联关系挖掘研究之路还很长,在后续的研究过程中将不断充实和完善关联学习理论与应用.
贡献声明:作者钱宇华提出从学习角度进行关联关系挖掘和关联学习的思想,并指导督促完成实验和论文;作者张明星、成红红共同给出关联学习的基本概念和形式化表达,制定实验内容并具体操作,撰写文章.三位作者同等贡献,共同一作.

