改进型格尼襟翼对不同实度的垂直轴风力机气动性能的影响

朱海天，郝文星，李 春，丁勤卫

（上海理工大学 能源与动力工程学院，上海 200093）

近年来，垂直轴风力机（vertical axis wind turbine，VAWT）由于其造价低、运行噪声小和适宜大型化等优势成为了研究热点［1-2］。然而，VAWT获能效率较之水平轴风力机低［3-4］，因此亟待一种有效且价格低廉的装置以改善VAWT 的气动性能。

格尼襟翼（Gurney flap，GF）是一种安装于翼型尾缘并垂直于弦线的平板。1978 年Liebeck［5］首次将GF 加装于翼型，并验证当GF 长度为1.25%c（c为弦长）时可极大地提升翼型气动性能。随后，经大量的相关实验与数值模拟研究与分析可知，GF 具有增大升力和增强流动控制的效果［6-15］。随着计算流体力学、实验方法和主动流动控制的快速发展，GF 的作用机理和应用范围得到了完善和扩大。Zhang 等［16］与Feng 等［17］将等离子激励器与GF 相结合研究其流动控制效果。Lee［18-19］研究了具有孔阵的GF对翼型气动性能的影响。Kinzel 等［20］研究了可摆动式GF 振荡翼型的动态特性。Graham 等［21］通过实验研究了GF 厚度对翼型气动性能的影响。Cole 等［22］研究了不同翼型加装GF 的增升效果。Ismail 等［23］与Shukla 等［24］将酒窝式翼型和GF 相结合以期增强GF 的流动控制效果。Xie 等［25］研究了GF对扑翼获能效率的影响。

文献[23-25]均对GF 应用于垂直轴风力机的发展做出了展望。因此，本文将GF 应用于垂直轴风力机并设计了一种改进型GF，通过数值模拟研究了两种格尼襟翼对不同实度的垂直轴风力机气动性能的影响，并基于对比研究验证计算模型的可靠性，分析具有GF 的VAWT 的风能利用系数、力矩系数和载荷波动在不同尖速比和不同实度下的数据。

1 空气动力学模型与网格模型

1.1 格尼襟翼模型及改型

半圆形凹槽是一种可在大攻角下通过反旋涡流抑制流动分离的被动流动控制技术［26］。本文将格尼襟翼与半圆形凹槽相结合以期提升VAWT的气动性能。为书写简洁，下文中改进型GF 在图中均称为dimple-GF。图1 为基于NACA0021翼型的两种GF 物理模型，图中：GF 高度hG、厚度LG分别为c的1.25%、0.04%；半圆形凹槽直径Dd与hG相等；尾缘与GF 间距SGT为c的10%。

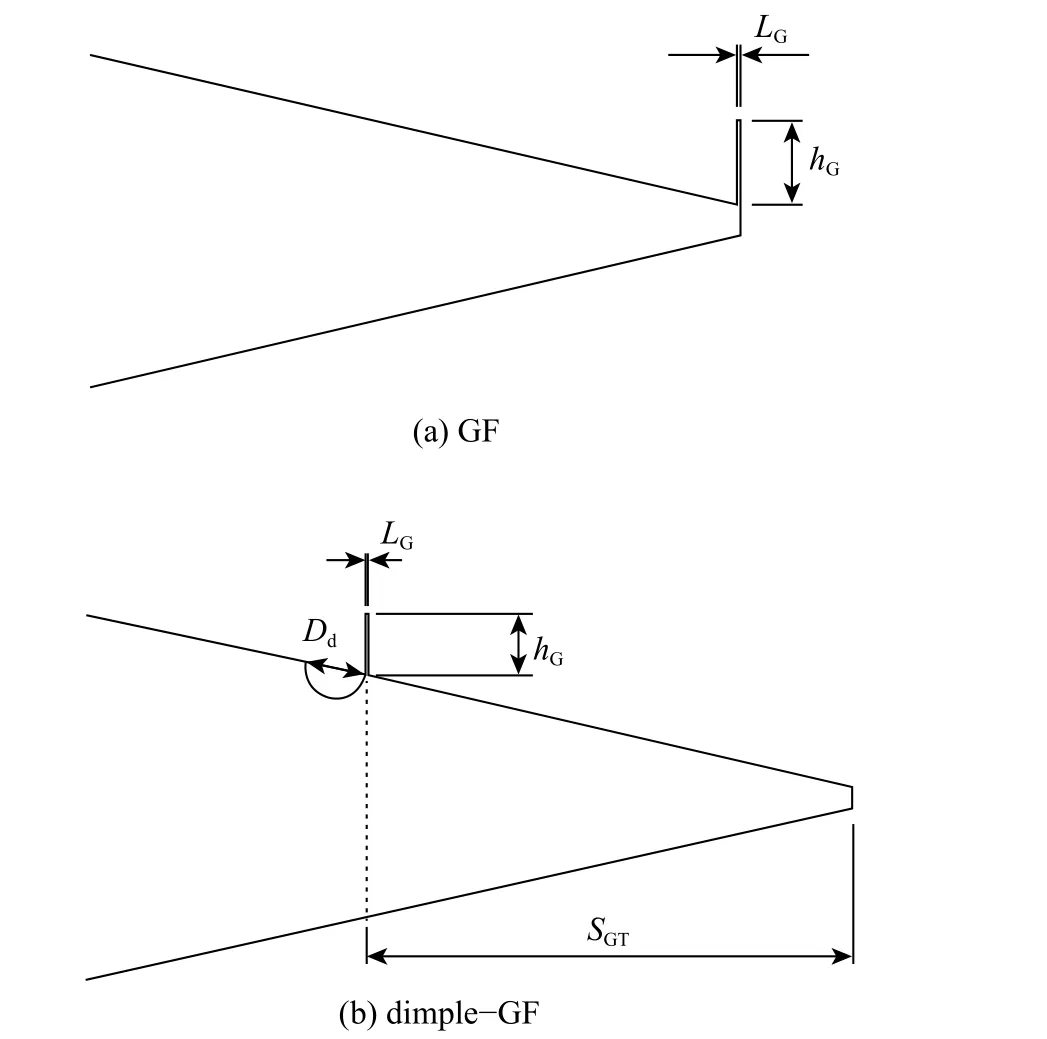
图 1 GF、dimple-GF 物理模型Fig. 1 GF、dimple-GF physical model

图2 为GF 翼型和改进型GF 翼型周围的网格模型。第一层网格高度满足第一层网格质心至壁面无量纲高度y+= 1，其网格最小正交质量分别为0.607 和0.528，网格最小畸变率分别为0.628和0.436。

1.2 垂直轴风力机模型

风能利用系数CP与 力矩系数Cm(θ)公式为

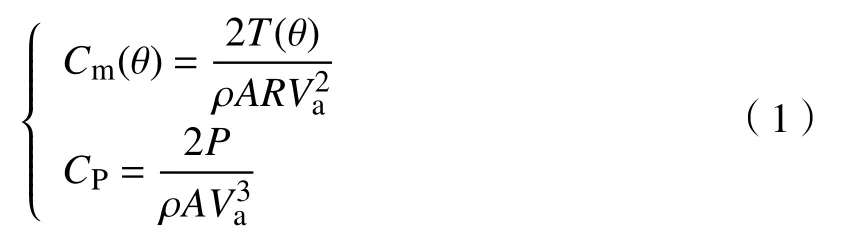
式中：T(θ)为 风力机在方位角 θ时所受的转矩，N·m-1；P为输出功率，W； ρ为空气密度，kg·m-3；A为 扫 风 面 积，m2；Va为 诱 导 速 度，m·s-1；R为旋转半径，m。

实度 σ为设计参数，下文中风力机半径保持不变。实度为0.175、0.250 对应叶片3（弦长分别为60.06 、85.80 mm），实度为0.333 对应叶片4（弦长与实度为0.250 对应叶片的一致），实度为0.416 对应叶片5，实度为0.500 对应叶片6。

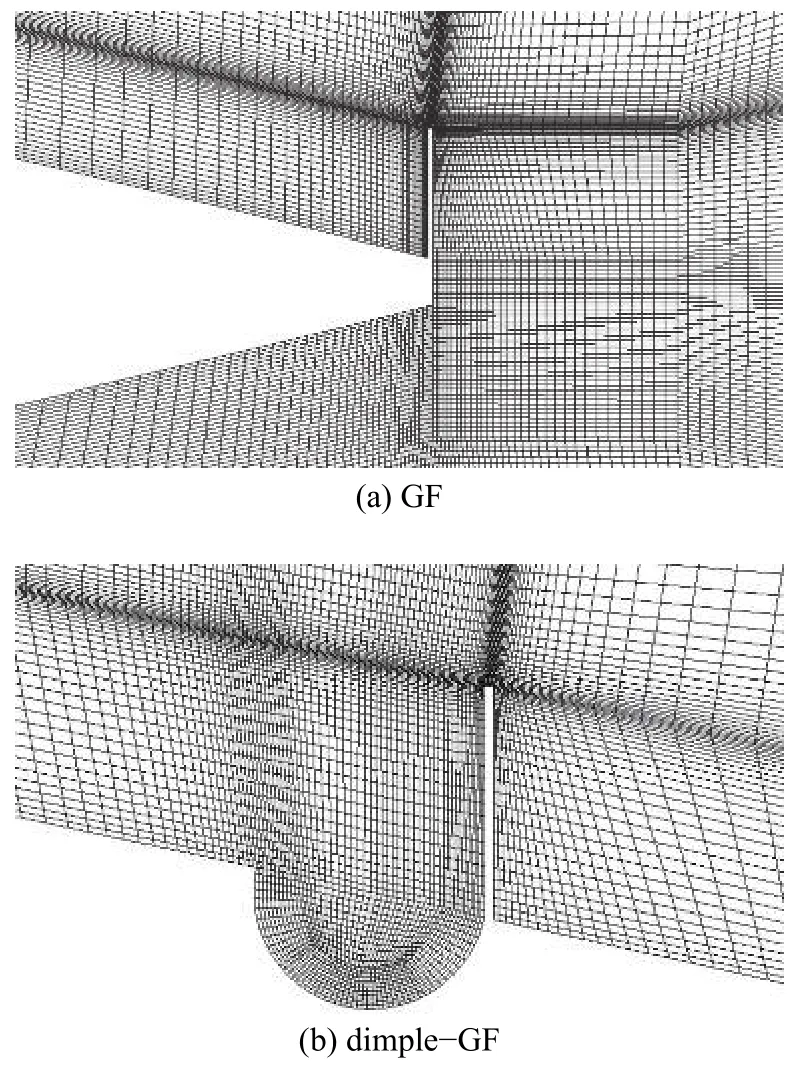
图 2 GF、dimple-GF 网格模型Fig. 2 GF、dimple-GF mesh model

式中，N为叶片数。

尖速比λ 反映垂直轴风力机运行工况，即

式中： ω为角速度，rad·s-1；V∞为来流速度，m·s-1。

图3、4 分别为VAWT 物理模型及拓扑结构，图中W为相对速度。除Z2 区域外，其他区域（Z1、Z3）均为结构网格。原始VAWT、具有原始GF 的VAWT、具有改进型GF 的VAWT 的总网格数分别为509 222、619 394 和656 264。

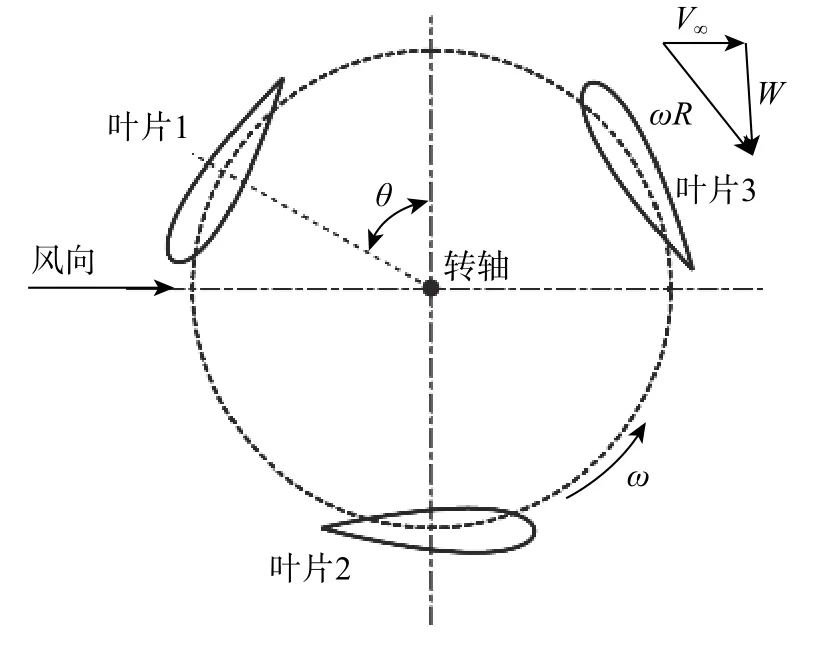
图 3 VAWT 物理模型Fig. 3 Physical model of VAWT

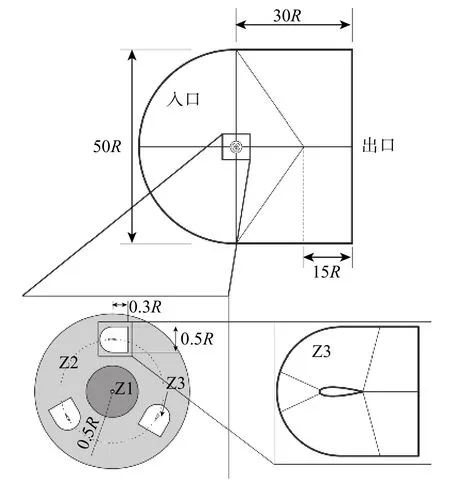
图 4 VAWT 拓扑结构Fig. 4 Topological structure of VAWT

2 计算模型的可靠性验证

2.1 数值算法及湍流模型

本文采用TSST 湍流模型。该湍流模型在捕捉层流至湍流的转捩时具有较好的精度，且在垂直轴风力机周围流场的数值计算中已广泛使用［27-28］。本文算例中壁面y+均取1，并均基于弦长的雷诺数，网格尺寸变化比例为1.05～1.08。采用Simplec 算法并均采用二阶迎风格式计算对流项，选用亚松弛因子以保证算法的收敛性。

2.2 边界条件

入口边界条件为速度入口，来流风速为9 m·s-1，入口湍流强度为3%，湍流黏性系数为1，空气密度为1.225 kg·m-3，空气动力黏度为1.789 4 ×10-5Pa·s，出口相对压力为0 Pa。

2.3 计算模型可靠性验证

本文选取展弦比为17 的SB-VAWT，通过获得单位扫风面积的风能利用系数，确定原始SB-VAWT 的风能利用系数，并与实验数据［29］进行对比。图5 为计算模型可靠性对比，研 究Standardk-ε 、Realizablek-ε 、SSTk-ω和TSST 湍流模型的模拟值和实验值的误差，以验证计算模型的可靠性。

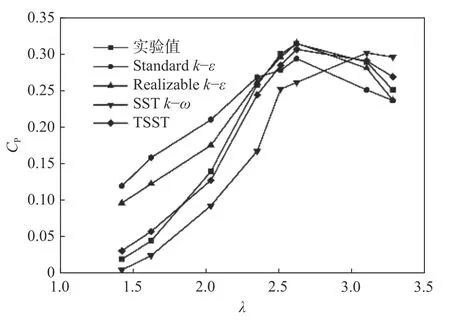
图 5 计算模型可靠性对比Fig. 5 Comparative study on the reliability of the computational models

由图5 中可知，TSST 湍流模型可较好地捕捉实验值。相比其他假设流体为全湍的湍流模型，TSST 湍流模型可更精确地计算低尖速比下VAWT 的气动性能。

本文采用网格收敛性索引（grid convergence index，GCI），建立基于具有改进型GF 垂直轴风力机的粗糙网格、中等精度网格和高精度网格模型，网格数分别为406 422、604 715 和901 254。图6 为采用不同网格模型时叶片切向力随方向角的变化。

由图6 中可知，中等精度网格和高精度网格模型的计算结果接近，而粗糙网格叶片所受推力低于高精度网格，粗糙网格、中等精度网格和高精度网格对应的SB-VAWT 的风能利用系数分为0.303 1、0.307 4 和0.309 0，对应的网格收敛率为-2.438。若采用安全系数为1.25，以中等精度网格的计算结果作为中间变量，得到的高精度网格GCI 为8 .56×10-3，中等精度网格GCI 为3.18×10-3。可见，中等精度网格模型也具有较好的收敛性。

图 6 在不同网格模型时叶片切向力随方位角的变化Fig. 6 Variation of tangential force of a blade with azimuth angles for different mesh models

3 结果与分析

图7 为具有两种GF 的VAWT 气动性能曲线，图中Clean 为原始风力机。由图7（a）～（e）中可发现，当尖速比为3.1、实度为0.250 时，原始格尼襟翼最大可提升10.92%的风能利用系数，改进型格尼襟翼最大可提升17.92%。在不同实度，改进型格尼襟翼在高尖速比时可较好地提升气动性能，而原始格尼襟翼在低尖速比时可较好地提升气动性能。

图7（f）为VAWT 整机的力矩系数随方位角变化的极曲线。由图中可知，随着实度的增加力矩系数曲线更趋近于类圆形，平均力矩系数越小，叶片平均受载均大于原始VAWT。

图7（g）为力矩载荷波动随尖速比的变化。由图 7（g）中可知，当实度大于0.333 时，载荷波动大幅削弱。当尖速比增大时，波动程度趋于缓和。当尖速比减小时，由于叶片失速更为严重，故波动程度将更为剧烈。特别地，与实度为0.250 时相比，实度为0.175 时载荷波动情况较好，这是由于较小的叶片弦长承受更小的载荷且叶片间干扰削弱。

4 结 论

本文采用Fluent15.0 软件进行数值模拟并分析得出GF 可大幅提升风力机气动性能。主要结论为：

（1）GF 和改进型GF 均可大幅提升VAWT 的气动性能，当尖速比为3.1、实度为0.25 时，原始GF 最大可提升10.92%的风能利用系数，改进型GF 最大可提升17.92%。改进型GF 更适用于高尖速比工况，而原始GF 适用于低尖速比工况。

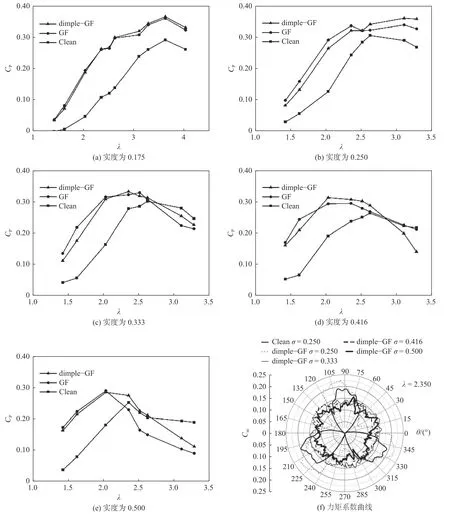
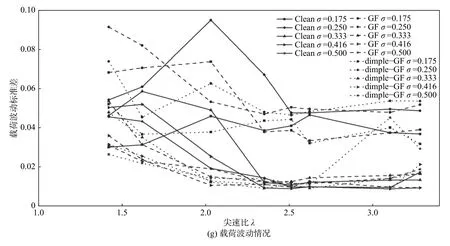
图 7 具有GF 的VAWT 气动性能Fig. 7 Aerodynamic performance of VAWT with GF

（2）随着实度增大，由于叶片间干扰导致风能利用系数降低，但载荷波动情况得到改善。实度为0.416 时，载荷波动情况最优。

GF 与其他被动流动控制或主动流动控制相结合是格尼襟翼未来发展的重点。本文就原始GF 和改进型GF 在不同实度的垂直轴风力机中的应用展开了研究，为选择较优的具有格尼襟翼的垂直轴风力机结构参数提供了参考。