基于多模光纤散斑的压缩感知在光学图像加密中的应用*
胡耀华 刘艳 穆鸽 秦齐 谭中伟 王目光 延凤平
(北京交通大学光波技术研究所, 全光网络与现代通信网教育部重点实验室, 北京 100044)
为了安全高效地对图像信息进行传输, 提出了一种新颖的基于多模光纤散斑的压缩感知结合双随机相位编码的光学图像加密方法.多模光纤产生的光斑作为压缩感知的测量矩阵, 完成对图像的第一次压缩和加密, 并且充当第一级密钥; 再利用双随机相位编码技术进行第二次加密, 实现对图像的完整加密过程, 随机相位掩模板充当第二级密钥, 解密过程与此相反.通过将光斑测量矩阵与用于压缩感知的常用随机测量矩阵进行对比研究后发现, 使用光斑测量矩阵解密后的图像质量更好, 而且相比于其他随机测量矩阵在硬件实现上的复杂性与高成本, 光斑矩阵可以很容易地通过简单的光学器件来获得, 且可以利用工作波长的改变来进行变换, 也即第一级密钥非常容易变换.同时经研究表明, 本文方法可以有效抵抗统计分析、噪声干扰和剪切等攻击, 且对密钥敏感性高, 具有良好的鲁棒性和安全性.因此, 本文提出的这种基于光斑矩阵的压缩感知与双随机相位编码结合起来的加密方法, 可以获得良好的加密效果与极大的密钥空间, 并且易于在光学领域整合.
1 引 言
随着多媒体技术应用的飞速发展, 通信环境中需传输的图像数据量日益增大, 对图像进行压缩和加密成为了图像安全有效传输的有力保障.由于基于光学理论的信息安全技术与传统的信息安全技术相比具有更多的优点[1], 针对图像的加密技术目前已成为光学信息安全领域的重要研究内容之一.Refregier和Javidi最早提出了双随机相位编码(double random phase encoding, DRPE)技术, 输入图像可在4f光学系统中转换成平稳的白噪声[2,3],从而实现加密.DRPE技术被提出来后受到了研究者的极大关注, 并在此基础上展开了更进一步的研究, 提出了许多新的方法[4−7].
虽然DRPE方法在一段时间内体现了很好的优势, 但在接下来的发展中却遇到了各种安全问题[8−10], 特别是, 它易受到基于相位检索技术的各种密码分析攻击.而产生这些安全问题的原因大多由于DRPE是线性过程, 引入压缩感知恰好可以解决这一问题.压缩感知是一种利用信号的稀疏性对信号进行压缩重建的技术, 打破了传统Nyquist−Shannon采样定理的限制, 可极大地降低采样的数据量[11,12].利用压缩感知的方法在加密的同时也直接压缩了要在信道中传输的图像数据量, 因此不同于文献[13]提出的结合压缩过程的加密方式, 其中压缩的意义只是选取部分有用的数据进行加密, 不会减少在信道中实际传输的数据量.同时, 压缩感知的方法也不同于文献[14]中提到的先压缩后加密的方法, 后者所需时间会较长.
基于上述优点, 利用压缩感知与DRPE技术结合表现出了很好的优势[15−21].文献[15]中提出了一种基于压缩感知以及双随机相位加密的空间复用多图像加密和解密技术, 该方法产生非线性加密系统, 能够克服传统DRPE的脆弱性.文献[16]中通过在分数傅里叶变换域中采用DRPE技术和压缩感知结合实现双图像加密, 除了完美的图像重建之外, 还指出压缩感知为传统的DRPE系统提供了额外的安全层.与之类似的还有文献[17], 区别在于DRPE变换域中采用了非线性分数梅林变换.而文献[18, 19]中在上述基础之上将得到的加密图像嵌入到一个宿主图像中进行信息隐藏, 但是这增加了系统的复杂性, 并且随着嵌入强度的增大, 会减弱隐藏信息的不可感知性和安全性.文献[20]中则将待加密图像先分成4个块, 然后单独进行压缩和加密, 每一次压缩感知使用的测量矩阵密钥都不相同, 这样会大大增加算法的时间复杂度.
本文通过将压缩感知与光学加密技术相结合,提出一种新的基于多模光纤散斑的压缩感知光学图像加密方案.利用多模光纤产生的光斑作为压缩感知中的测量矩阵, 对图像进行压缩和第一级加密, 然后利用DRPE技术对图像进行第二级加密,这样两级加密可以大大扩展密钥空间, 使得攻击者很难破解密钥.通过分析证明采用这种方法加密解密时可以获得比使用常用的随机测量矩阵时更好的图像质量.相比于其他测量矩阵在硬件实现上的复杂性与高成本, 光斑矩阵可以简单地利用多模光纤而得到.而且, 由于多模光纤中模式传输与干涉效果对波长的敏感性, 光纤光斑将随着光源波长的改变而改变, 因此可以非常灵活方便地通过改变光源波长来实现对基于光斑的压缩感知中的测量矩阵进行高效更新.同时, 又由于使用多模光纤散斑的压缩感知可以在光学域实现, 这为后续将其与DRPE技术在光学领域的整合提供了可能.研究结果表明该方案能够大大降低图像的采样数据量、鲁棒性好、对光斑密钥响应敏感, 并可以抵御统计分析、噪声污染和数据丢失等很强的攻击.
2 理论知识
2.1 压缩感知
压缩感知理论指出, 当信号可在某一基下稀疏表示时能够通过少量的测量数据对信号进行重构,大多数的图像信号都是可以满足这一要求的.对信号进行压缩感知时主要包含测量和重建的两个步骤, 假设x是长度为N的输入信号, 测量过程可以表示为

式中Φ是M × N的测量矩阵, y是M × 1的测量值.考虑到原始输入信号x本身一般不稀疏, 所以先将信号x稀疏表示, 于是, 压缩感知的测量过程可进一步表示为

式中Ψ为正交稀疏基, ξ是稀疏基下的系数向量,Θ=ΦΨ被称为传感矩阵, 当Θ满足受限等距性质[22]时, 能够通过求解最优化问题高精度复原系数向量ξ, 用数学表示为:

其中 ∥ ·∥1表示L1−范数, 上述问题属于凸优化问题,可以通过某些恢复算法来求解出系数向量ξ, 最后再恢复出原始输入信号x.本文中所采用的恢复算法是基追踪(basis pursuit, BP)算法.
2.2 多模光纤端面光斑图样
多模光纤由于其中存在的多个模式之间的干涉会在输出端面处形成明暗不均的散斑图样, 即光斑图样, 光斑的分布情况将由多模光纤所处空间环境、光源及激发状态等决定.将光源通过单模光纤与多模光纤偏芯连接后(如图1所示), 当光注入到多模光纤时, 由于场的中心激发性被破坏, 因此可在多模光纤中激发出大量的非圆对称高阶传输模式[23], 而大量传输模式之间相互发生干涉就会在光纤端面处出现相比于中心激发方式更为复杂随机的光斑图样.本文所用的光斑都是利用图1所示的装置经过实验测得, 然后传到计算机中做后续的仿真处理, 图中也给出了波长为1550 nm的光对多模光纤进行偏芯激发时产生的典型光斑图样.
2.3 光斑矩阵的构造
在利用图1装置获得合适大小的光斑图像后对光斑图像进行相应的处理, 使之成为后续压缩感知中的测量矩阵, 构造过程如图2所示.首先考虑到光斑图像呈现出的是圆形, 而最终矩阵应该是方形, 所以先对圆形的光斑图像进行切割, 提取其内切正方形, 接下来对内切正方形区域进行灰度转换得到灰度图像, 将其像素值归一化处理后即可得到以灰度像素值为元素的N × N矩阵, 最后再根据所需要的压缩比提取N × N矩阵中的M行即可得到压缩感知中所需要的测量矩阵.

图1 多模光斑产生装置(LD, 半导体波长可调激光器; SMF, 单模光纤; MMF, 直径为105 µm的多模光纤, 长度为5 m; IR, 近红外相机)Fig.1.Multimode specklegram generator (LD, laser diode; SMF, single mode fiber; MMF, multimode fiber; IR, infrared camera).

图2 光斑矩阵构造流程示意图Fig.2.Flow chart of the construction method of the fiber specklegram based measurement matrix.
2.4 双随机相位编码
DRPE技术是一种经典的加密方法, 可用4f光学系统来实现(图3).原始待加密图像 f (x, y) 经过输入平面上的随机相位掩模板(random phase mask, RPM) RPM1进行第一次调制, 然后通过透镜进行傅里叶变换, 接着经过频谱面上的RPM2进行调制, 最后经过透镜进行傅里叶逆变换, 从而在输出面上获得类似于平稳白噪声的加密图像g(x, y).由于光路的可逆性, 解密是加密的逆过程.
在加密过程中, RPM1和RPM2可分别表示为

式中 ( x,y) 和 ( u,v) 分别表示空域和频域坐标, 而a(x,y)和 b (u,v) 则分别为空域和频域中的随机相位函数, 它们都是在[0, 1]上均匀分布的随机序列,对输入光可产生0—2π的相位延迟.因此双随机相位加密和解密用数学过程可表示为

其中, FT表示为傅里叶变换, F T-1表示为傅里叶逆变换, *表示共轭.

图3 基于4f的光学DRPE系统Fig.3.Optical DRPE system based on 4f.
3 加密解密方案流程图
采用本方案对图像进行加密解密时的流程图如图4所示, 首先原始图像经过压缩感知完成压缩和第一次加密, 光斑充当测量矩阵和第一级密钥,然后再用DRPE加密得到密文图像在信道中传输,随机相位板充当第二级密钥, 在接收端实现加密的逆过程即可解密出图像.为了验证上述方案的可行性, 对像素大小为256 × 256的Lena图像进行了加解密, 加解密过程中的图像变化如图4中A—E点所示, 可以看出解密图像和原始图像在视觉上很一致, 并且在加密过程中还完成了压缩, 表明本方案是可行的.

图4 基于多模光纤散斑的压缩感知光学图像加密解密过程流程图Fig.4.Flow chart of compressive sensing optical image encryption and decryption based on multimode fiber specklegram.
4 解密效果分析
4.1 光斑矩阵与常见测量矩阵解密图像质量对比分析
由于在进行压缩感知时普遍使用随机高斯矩阵等作为测量矩阵, 而本文是采用更加容易利用硬件实现的光斑矩阵作为测量矩阵, 因此本文通过与采用高斯(Gauss)矩阵、Bernoulli矩阵、Hadamard矩阵和Toeplitz矩阵的情况进行对比来衡量所提出方案的性能.为了能够客观地评价解密图像的质量, 引入了峰值信噪比(peak signal to noise ratio,PSNR), 定义为

式中 M ×N 为原始图像的大小, g (m,n) 为解密图像, f (m,n) 为原始图像, k表示图像像素灰度值的位数, 通常灰度图像的k为8, 也即有256个灰度级.图5中特别给出了在不同压缩比情况下采用光斑矩阵和高斯矩阵时对应的解密图像, 另外也给出了使用其他测量矩阵时对应解密图像的PSNR随压缩比的变化曲线.可以看出使用光斑测量矩阵时解密图像质量更好.
为了更好地表明使用本方法得到的最终解密图像的质量更优, 将本方法与文献[15, 18, 20]进行了比较, 在相同压缩比的情况下, 最终解密图像的PSNR对比如表1所列.可以看出使用本方法解密出来的图像质量是最高的.

表1 解密图像质量分析Table 1.Decrypted image quality analysis.

图5 光斑矩阵和高斯矩阵对比分析 (a)−(d)使用光斑矩阵在压缩比为0.3, 0.5, 0.7, 0.9时的解密图像; (a')−(d')使用高斯矩阵在压缩比为0.3, 0.5, 0.7, 0.9时的解密图像; (e)使用不同测量矩阵时对应解密图像的PSNR随压缩比的变化Fig.5.Comparative analysis of specklegram matrix and Gaussian matrix:(a)−(d) The decrypted image using specklegram matrix at compression ratio of 0.3, 0.5, 0.7, 0.9; (a')−(d') the decrypted image using Gaussian matrix at compression ratio of 0.3, 0.5, 0.7, 0.9;(e) comparison between the PSNRs of the decrypted images varying with the compression ratio when using different measurement matrices.
4.2 直方图和相关性分析
图像中的像素间往往具有某种分布规律, 攻击者很容易对像素进行统计分析得到图像的有用信息.为了验证本文方案抵抗统计攻击的能力, 分别对3幅经典图像分析了原始图像和密文图像的直方图和相关性.如图6所示, 第1列为原始图像,第2列为对应的直方图, 第3列和第4列分别为密文相位和幅值的直方图.可以看出尽管原始图像的直方图非常不同, 但密文相位和幅值的直方图在分布上彼此相似, 这表明攻击者无法从密文的直方图分析中获取有用的信息.
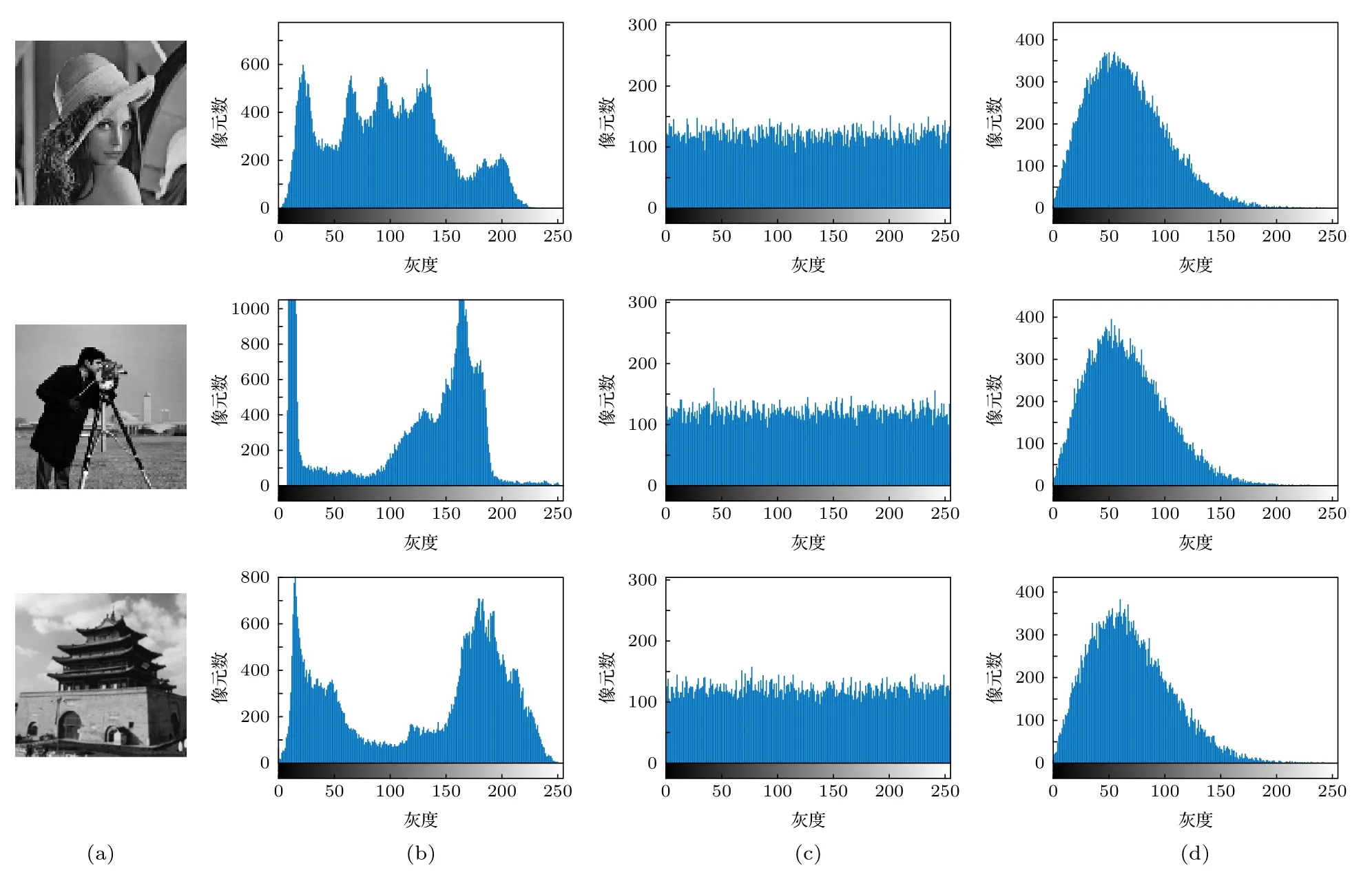
图6 直方图分析 (a)原始图像; (b)原始图像对应的直方图; (c)密文的相位直方图; (d)密文的幅值直方图Fig.6.Histogram analysis:(a) Original image; (b) histogram corresponding to original image; (c) phase histogram of ciphertext;(d) amplitude histogram of ciphertext.

图7 相关性分析 (a)−(c)分别为明文图像在水平、垂直和对角方向上的像素相关性分布; (d)−(f)分别为密文图像在水平、垂直和对角方向上的像素相关性分布Fig.7.Correlation analysis:(a)−(c) Pixel correlation distributions of plaintext images in horizontal, vertical and diagonal directions;(d)−(f) pixel correlation distributions of ciphertext images in horizontal, vertical and diagonal directions.
在有意义的图像中, 相邻像素通常具有强相关性, 为了分析原始明文图像和密文图像相邻像素的相关性, 分别从Lena明文图像及其对应密文图像的水平、垂直和对角方向随机选取9000对像素进行相关性分析, 并画出了像素的相关分布图, 如图7所示, 可以看出, 在水平、垂直、对角方向上, 明文图像像素的相关性都很强, 而密文像素的相关性较弱.因此本方法可以有效地打破原有图像像素的相关性, 对像素进行很好的扩散.
此外, 为了更直观地表明相关性, 采用相关系数来计算源图像和密文图像像素在不同方向上的相关性.相关系数(correlation coefficient, CC)定义为

其中N为选取的相邻像素对数, xi和 yi分别为两个相邻像素的灰度值, 不同方向上相邻像素的相关系数如表2所列.可以看出明文图像相邻像素的相关系数在3个方向上都很大, 而密文图像则很低,所以本方案的加密过程可以有效地混淆和扩散图像像素, 因此其能够抵抗统计分析攻击.
此外, 也将本文方法与文献[17, 20]中的像素相关系数进行了对比, 对于Lena图像, 其加密后图像像素的相关系数如表3所列.可以看出, 使用本文方法进行加密后的图像像素相关系数要比文献[17, 20]中的低一个数量级, 因此, 本文提出的加密方法对于扩散图像像素具有明显优势.

表2 相邻像素的相关系数Table 2.Correlation coefficient of adjacent pixels.

表3 加密图像像素相关系数Table 3.Correlation coefficient of encrypted im−age pixels.
4.3 抗噪声分析
考虑到密文图像在现实通信环境中容易受到噪声干扰, 也对本方法的抗噪声性能进行了分析,分别对密文图像添加均值为0, 方差为0.1到0.9的高斯白噪声后进行解密, 图8(a)—(d)给出了密文图像中噪声方差为0, 0.1, 0.3和0.5时的解密图像, 图8(e)为噪声方差和解密图像PSNR的关系图, 可以看出加噪声后的解密图像与不加噪声后的解密图像质量基本相同, 由此可见该方案具有抗噪声干扰的鲁棒性.
4.4 抗剪切分析
还对本方法的抗剪切能力进行了分析, 分别对密文图像从水平、垂直、中心和边角4个方向进行不同程度的剪切攻击, 图9给出了受到剪切攻击的密文图像及其对应的解密图像.可以看出, 解密图像中依然能够分辨出主要的图像信息, 表明本方法能够有效抵抗剪切攻击.

图8 抗噪声分析 (a)−(d)在密文图像中分别加入方差为0, 0.1, 0.3和0.5的噪声时的解密图像; (e)密文图像中加入噪声后的解密图像PSNR随相应噪声方差的变化Fig.8.Anti−noise analysis:(a)−(d) Decrypted images with noise of 0, 0.1, 0.3 and 0.5 variances added to ciphertext image respect−ively; (e) curves of relationship between noise variance and the PSNR of decrypted image with noise in ciphertext mage.

图9 水平、垂直、中心和边角方向不同程度的剪切攻击和剪切攻击后的解密图像 (a)垂直剪切10%; (b)垂直剪切50%; (c)水平剪切10%; (d)水平剪切50%; (e)中心剪切; (f)边角剪切; (a')垂直剪切10%解密图; (b')垂直剪切50%解密图; (c')水平剪切10%解密图; (d')水平剪切50%解密图; (e')中心剪切解密图; (f')边角剪切解密图Fig.9.Cropping attack of different degrees in horizontal, vertical, central, corner directions and decrypted image after cropping at−tack:(a) Vertical cropping 10%; (b) vertical cropping 50%; (c) horizontal cropping 10%; (d) horizontal cropping 50%; (e) central cropping; (f) corner cropping; (a') decrypted image after vertical cropping 10%; (b') decrypted image after vertical cropping 50%;(c') decrypted image after horizontal cropping 10%; (d') decrypted image after horizontal cropping 50%; (e') decrypted image after central cropping; (f') decrypted image after corner cropping.
4.5 光斑密钥敏感性分析
密钥敏感性也是加密方法的一个重要性能指标.图10给出了原始光斑密钥及对应的解密图像,以及修改后的光斑密钥及对应的解密图像, 图中两个光斑是利用不同的工作波长(波长差为0.1 nm)获得的, 可以发现从解密图像(图10(d))中分辨不出原始图像的内容.为了比较解密图像和原始图像之间的差异, 引入了均方误差(mean squared error,MSE), 定义为

式中 f (i,j) 和 g (i,j) 分别为原始图像和解密图像在位置 ( i,j) 处的像素值.使用在相同光纤结构不同波长入射光情况下实验产生的光斑进行解密, 图10(e)给出了MSE曲线, 图10(f)为图10(e)波长下对应的光斑, 波长间隔为0.1 nm.可以看出, 尽管两光斑矩阵的工作波长相差很小, 亮斑分布方式接近,但是利用另一个光斑矩阵进行解密时, 完全无法获得原始图像, 只有当加密的光斑密钥和解密的光斑密钥来自于同一工作波长产生的光斑时, MSE数值接近于0, 其他情况下的MSE都很大, 这说明解密过程对光斑密钥很敏感, 同时也说明通过改变光源工作波长来获得不同密钥的可行性.

图10 光斑密钥敏感−性分析 (a)原始的光斑密钥; (b)修改后的光斑密钥; (c)与(a)相对应的解密图像; (d)与(b)相对应的解密图像; (e)使用15501551.9 nm (间隔为0.1 nm)工作波长产生的光斑进行解密的MSE曲线; (f)对应于(e)中使用的实验测得的不同工作波长光斑Fig.10.Specklegram key sensitivity analysis:(a) Original specklegram key; (b) modified specklegram key; (c) decrypted image cor−responding to (a); (d) decrypted image corresponding to (b); (e) MSE curve for decryption using specklegram generated at different wavelengths; (f) the corresponding specklegram at 1550−1551.9 nm with a wavelength interval of 0.1 nm.
5 结 论
提出了一种新的基于多模光纤端面光斑的压缩感知光学图像加密方法, 多模光纤产生的散斑作为压缩感知过程中的测量矩阵不仅完成了对图像的压缩, 还扮演着第一级密钥的作用.随后将压缩感知与DRPE相结合, 成功地实现了对图像的双重加密.通过对光斑矩阵和常用的随机测量矩阵用于压缩感知并对图像进行加密解密后的性能进行了对比分析, 发现使用光斑矩阵时解密出来的图像质量更好, 并且在具体实现方式上, 光斑矩阵可以由非常廉价的多模光纤得到, 使得压缩感知能够在光学域实现, 这也为进一步将压缩感知和DRPE在光学域的整合提供了依据.同时, 也从有效性和安全性的角度对本方案的性能进行了进一步的分析, 结果表明, 此加密方案可以打破原有图像像素的相关性, 有效地混淆和扩散图像像素, 有效地抵抗统计分析、噪声污染、数据丢失等攻击, 对密钥的敏感性强、安全性高.而且由于可以利用不同工作波长获得不同的光斑作为第一级密钥, 与DRPE结合以后, 将可以获得极大的密钥空间.

