基于改进人工势场的无人机预设航线避障研究①

马娅婕 刘国庆 胡 轶 张 磊

(武汉科技大学冶金自动化与检测技术教育部工程研究中心 武汉 430081)

0 引 言

随着传感技术和嵌入式系统的快速发展，无人机自主性日益提高，在实际应用中，无人机难免遇到障碍物，因此避障功能一直是研究热点。环境信息的获取手段多种多样，例如相机[1]、激光[2]、热成像[3]和超声波等；实时效果好的避障算法有A*算法、爬行虫算法及人工势场法等。其中人工势场法由于其计算量小，实时性好，避障轨迹平滑，被广泛应用。

传统的人工势场法只考虑能否安全到达目标点，目前有很多的改进算法致力于提高避障平滑性、改善避障轨迹、逃离极小点。例如文献[4]通过对人工势场法增设额外控制力，能够帮助机器人主动逃离极小点。文献[5]采用混合经验的改进人工势场法使得机器人能够适应多种形状的障碍物。文献[6]结合最优控制和人工势场法实现了无人机的自主飞行控制。文献[7]在人工势场法中引入距离因子实现了无人机编队之间的距离保持。文献[8]对势场引入局部约束函数，实现了机器人的动态避障。此外，人工势场法在机器人避障上广泛应用，如卫星编队避障[9]、伴随机器人避障[10]。但是上述改进算法无法完成基于预设航线的无人机避障。文献[11]提出了线势场的概念。文献[12]实现了基于直线航线的避障。但是该算法仍然存在不足之处，避障过程不够平滑，无法跟踪曲线航线。因此本文针对曲线航线跟踪对人工势场法进行改进，并应用Adams[13]构建仿真场景，进行仿真验证。

1 人工势场法改进

1.1 传统人工势场法的局限性

人工势场法是由Khatib[14]提出的一种虚拟力法。它的基本思想是将移动机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动，目标点对移动机器人产生“引力”，障碍物对其产生“斥力”，最后通过求合力来控制移动机器人的运动。将人工势场法运用到无人机的避障中，如图1所示，用小球表示无人机，较大球体表示障碍物。

图1 传统人工势场法

人工势场法是通过计算当前位置势函数的负梯度方向作为无人机下一步的运动方向，引力势函数和斥力势函数分别为Uatt(q)和Urep(q)：

(1)

式中，q为无人机当前位置，ρ(g)为无人机距离目标点距离，ρ(q)为无人机距离障碍物表面距离，ρ0为障碍物有效影响范围，ξ为引力场系数，η为斥力场系数。

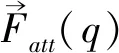
(2)

式中，▽ρ(g)为单位矢量，方向由目标点指向无人机，▽ρ(q)也是单位矢量，方向为障碍物指向无人机。此时无人机所受合力为

(3)

传统的人工势场法可能使无人机陷入局部最小点，在局部最小点时，无人机所受到的目标点的引力和障碍物的斥力大小相等，方向相反，即所受合力为0，而且速度也为0，无人机在该点静止，避障失败，如图2所示。

图2 传统人工势场法局部最小点

1.2 线势场的引进和改进

本课题组避障研究基于预设航线跟踪，此时引力场不再是由目标点产生，而是由目标航线产生,引入线势场的概念[9]。

引力场由预设航线产生：

(4)

式中，ρline(g)为无人机距离预设航线的距离，▽ρ(g)为预设航线指向无人机的单位矢量。线势场的作用是产生使无人机靠近预设航线的力，这实质上是反馈控制，最终目的是为了消除位置误差。

图3是预设航线为直线时的情况，在无人机执行不同的任务时，预设航线也有可能为曲线，下面以正弦航线为例给出当预设航线为曲线时的情形。当预设航线为曲线时，基于预设航线的人工势场避障方法要求当无人机在障碍物影响范围外时，无人机能够跟踪预设航线。

图3 线势场引入

单纯的位置反馈控制无法消除曲线跟踪的误差，在这里引进前馈和速度控制，令

(5)

式中，vX为无人机沿X轴方向的速度，ρcurve(g)为无人机距离预设航线距离，ΔT为控制周期，ΔVY为预设轨迹和实际轨迹的Y向速度差，θ为速度差系数，两者的存在是为了消除航线跟踪误差，将在2.3节证明。

1.3 斥力场的改进

由文献[11]可知，基于线势场和传统斥力场的无人机避障轨迹不理想，本文进行斥力场改进，将斥力场的方向改为平行于Y轴，如图4所示。改进后的斥力为

(6)

式中除▽ρ(q)发生变化外，其余参数均与式(2)相同。▽ρ(q)为单位矢量，具体方向为

(7)

式中，yq为无人机位置的纵坐标，y0为障碍物中心的纵坐标。

图4 斥力场改进

采用改进后的人工势场法，无人机在X轴上所受势场合力为0，为完成基于预设航线的避障任务，给定无人机X轴方向一个合适的速度。

斥力场改进之后对避障和无人机控制进行了优化： (1) 增强了无人机的可控性； (2) 可自主逃离局部最小点。

由于无人机X轴速度可根据任务要求和环境给定，如果环境复杂且探查半径较大，可将速度设定为较小值；如果环境简单且探查半径较小，可将速度设定为较大值。该方法提高了任务速度，极大地增强了无人机的可控性。

局部最小点是无人机所受引力和斥力合力为0的点，在该点处，无人机有沿X轴的速度，在下一周期，无人机X轴的位置发生变化，所受合力不再为0，即无人机自主逃离局部最小点。

2 Adams仿真

2.1 Adams简介及环境搭建

Adams即机械系统动力学自动分析，可用于预测机械系统的性能、运动范围、碰撞检测、峰值载荷以及计算有限元的输入载荷等。相比于其他无人机避障仿真软件如Matlab和VC等，Adams不仅可以更加直观地观察无人机的运动过程，而且还可以对无人机所受的力、加速度、速度等信息进行更加细致的分析，此外Adams更是避免了大量的矢量编程。

用Adams中View分别搭建基于直线航线和曲线航线的2种避障场景，本课题组完成了无人机的基本控制和高度控制[15]，在这里将无人机等效为单位质量、单位直径的小球(以下称无人机)，障碍物分别为半径不同的2种无穷质量的大球，为了检验无人机的航线跟踪能力，建立一个辅助球并给它合适的初始X方向速度和Y方向位移，使其产生高度为0(方便计算)、航线为直线和正弦曲线的2种轨迹。本文无人机应用场景是地表近距离，所以研究目标为实现三维避障算法。给定无人机一个3向合力，分别在Y轴和Z轴输入引力和斥力的合力，进行避障仿真。

2.2 线引力为定值和变量的对比验证

文献[7]在其改进算法中提出为了提高无人机的可控性将引力改为定值，在此采用二维避障场景验证2种方法的优劣性，场景设计如图5所示，参数分别为ρ0=5 m，ξ=100，η=100，常量引力为800。

由图6和图7可知，2种方法均可完成基于预设航线的无人机避障，且定引力的轨迹确实相对变引力的轨迹能更好地跟随预设航线。但是定引力曲线有微小抖动，平稳性不好，分析2种方式在避障过程中的速度，由图8可知引力为定值时Y轴速度抖动太大，而引力随距离变化时速度较为平缓，综合分析可以看出引力随距离变化时避障效果更为明显。

图5 仿真场景设置

图6 引力为定值和变量时的轨迹对比

图7 引力为定值和变量时的Y向位移对比

图8 引力为定值和变量时的Y轴速度对比

2.3 引入前馈和速度的线势场对比验证

仿真场景设置3个单位质量的小球，分别为预设轨迹球、前馈+反馈的线势场跟踪球和单纯反馈的跟踪球。3球均给定X向的恒定速度，预设轨迹球给定Y方向的正弦位移(以正弦曲线为例)，2跟踪球受到线势场作用力，分别为

(8)

仿真结果如图9所示，单纯位置反馈控制的线势场无法消除跟踪曲线航线的误差，而引入前馈和速度控制的线势场能够极大地削弱甚至消除跟踪曲线航线的误差，跟踪效果良好。

图9 线势场引入前馈和速度控制前后曲线跟踪Y向位移

2.4 基于改进人工势场法的三维避障实验

课题组已经完成无人机的基本控制和定高算法，避障原则采用较低障碍物越过、较高障碍物绕过的思路，即水平和竖直方向分别采用改进后的人工势场法。预设航线为正弦曲线，Z坐标为0，即不进行高度控制验证。避障场景如图10所示。无人机用半径0.5 m的单位质量球代替，出发点(-30, 0, 0)，低矮障碍物半径2 m，球心位于(-15, -7, 0)，3个较高障碍物半径依次为5 m、5 m、6 m，位置依次为(-15, 1, 0)、(1, 3, 0)、(15, 7, 0)，单位为m。

预设航线为航点(-30, 0, 0)到航点(30, 0, 0)之间的正弦曲线，轨迹方程为

(9)

给定无人机在XY平面所受势场引力为

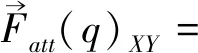
·▽ρ(g)

(10)

在XZ平面所受势场引力为

(11)

单个障碍物产生的斥力为

(12)

无人机初始速度为vx=1 m/s。进行60 s三维避障仿真。仿真结果如图11～图14所示。

由图11～图13可以看到，改进后的人工势场法可以在完成避障的同时尽量追踪预设航线，满足避障要求。下面分析无人机避障过程中的速度，判断避障轨迹是否平滑。通过图14可知整个避障过程中无人机各向速度均小于6 m/s，速度处于可控范围内，并且没有较大抖动，轨迹较为平滑。轨迹图和速度曲线表明该算法能够平滑完成基于预设航线的无人机三维避障。

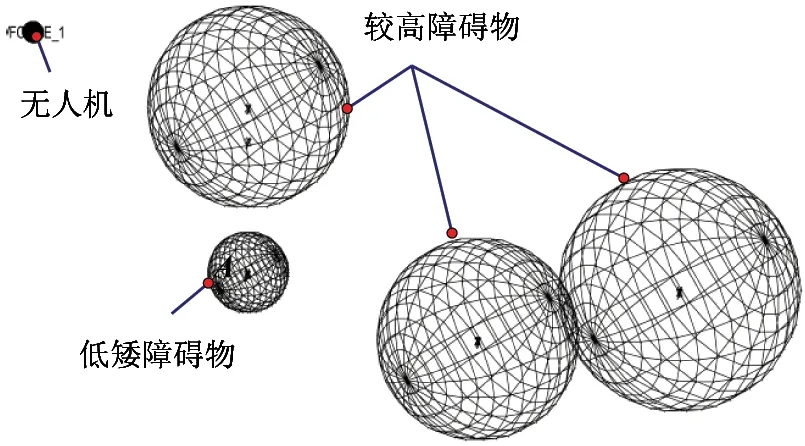
图10 三维仿真场景构造

图11 三维避障仿真结果

图12 三维避障仿真结果XY投影

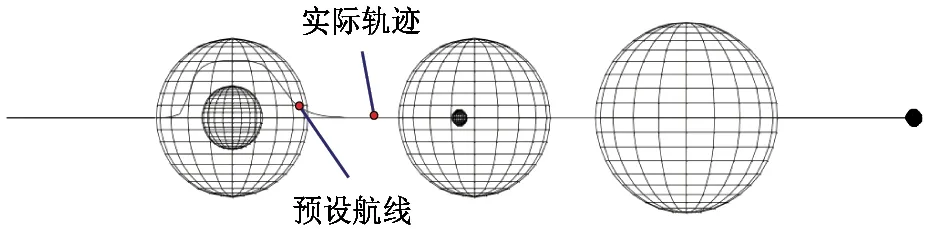
图13 三维避障仿真结果XZ投影

图14 无人机避障过程3向速度

3 结 论

针对目前无人机许多场合需要用到基于预设航线的三维避障，对传统人工势场法进行了改进，将引力场改为航线势场，并加入速度势场和前馈控制，将斥力场方向改为垂直于航线，消除了局部最小点。基于Adams构建三维避障场景，运用改进引力线势场进行航线跟踪，跟踪曲线更加精确和平滑；运用改进人工势场法能够完成基于预设航线的无人机三维避障，而且避障轨迹较为平滑。