U形渠道斜坎平顶量水堰优化研究

孙娟娟，张 兵，陈小松

(湖北省水利水电规划勘测设计院，湖北 武汉 430064)

灌区量水是灌区现代化建设的重要内容，对提高灌区管理水平具有重要意义和价值[1]。随着我国灌区改造工程的大量实施，U型渠道凭借其水沙条件优越以及占地面积较小等诸多优势，被广泛应用于灌区的斗渠和以下渠道建设，而与之配套的量水设施研究也获得诸多成果，出现了圆头量水柱[2]、直壁式量水槽[3][4]、喉道测流槽[5]等诸多不同形态的量水设施。但是，这些量水设施主要适用于底坡坡度较小的渠道。随着水利工程建设的不断深入，在丘陵山区建设的U型灌溉渠道往往具有较大的底坡坡度，而这方面的量水设施研究较为欠缺。基于此，美国水利工程专家普罗格尔和鲍斯通过多次试验研究，提出了适合底坡坡度较大的渠道量水的斜坎量水堰。鉴于这种量水结构具有便于安装、准确度高以及测量方便等诸多优势，我国水利水电部结合我国的实际情况对斜坎量水堰进行参数补充，并在我国的灌区进行推广。目前，国内关于斜坎量水堰的研究主要集中于传统的矩形和梯形渠道，对U型渠道斜坎量水堰测流方面的进行的相关研究不多。因此，如果将该量水堰应用于灌区斗渠及以下渠道，还需要在水力特性方面进行更多研究。在这方面，西北农林大学胡笑涛教授基于模型试验的方法提出了在斜坎量水堰的末端加上水平段的斜坎平顶量水堰，可以有效减小跌落水流对渠道底部的冲击，使量水堰末端水流更为平稳[6]。基于此，本文利用FLOW- 3D软件进行模型构建，利用数值模拟的方法进行斜坎平顶量水堰堰顶长度对U形渠道测流影响的相关研究，为斜坎量水堰的推广提供必要的依据[7- 13]。

1 FLOW- 3D的构建

1.1 FLOW- 3D软件简介

从事水利工程的研究者一直希望有一套能够处理复杂自由液面的流体力学分析软件，而FLOW- 3D以优异的计算方法和能力解决了上述问题[14]。该软件是国际知名流体力学专家Dr.C.W.Hirt的毕生之作，在1985年正式推出之后，在实际问题模拟和计算结果的准确度方面均得到实际应用结果的验证，特别是其中的FAVOR模块更是凭借对自由液面等复杂水利问题给出了更为精确和高效的解决方式。该软件主要包括几何模型导入、网格设定和生成、边界条件的定义、计算求解以及结果后处理等几个主要部分，使用者可以凭借该软件完成从模型建立到结果输出，而不需要其他软件进行处理。

1.2 模型的建立

本次研究以某大学的斜坎量水堰试验模型为几何原型，利用Auto CAD构建同一尺寸的U型渠道和斜坎量水堰三维模型。在模型建立过程中，渠道断面底部圆弧的圆心作为模型的坐标原点，指向右侧边壁的方向为X轴正方向，顺水方向为Y轴的正方向，竖直向上的方向为Z轴的正方向，如图1所示。

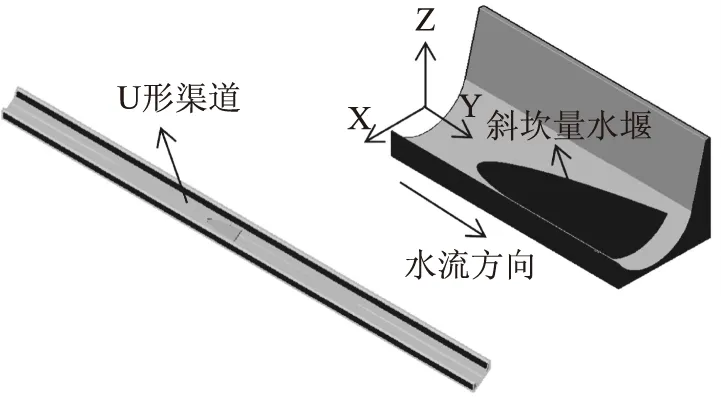
图1 模型示意

1.3 控制方程

研究中将渠道内的水流视为符合基本物理守恒定律的牛顿流体，斜坎量水堰的测流利用N- S方程和连续性方程进行描述[15]，其数学表达式如下：

(1)

(2)

式中，ρ—流体密度，kg/m3；t—流动时间，s；u—流体速度，m/s；μ—粘滞系数；p—流体压强；f—流体受到的质量力。

在Flow- 3D中，有六种湍流模型可用，分别是Prandtl混合长度，单方程，两方程κ-ε，RNGκ-ε、κ-ε以及大型涡流模拟LES模型。当渠道中的水流以一定的流速经过斜坎量水堰时，由于受到堰体的顶托作用，流态会发生比较显著的变化，因而呈现出十分明显的三维特征，因此本次研究中选用RNGκ-ε模型。

1.4 网格剖分

将上节建立的量水堰Auto CAD三维模型导出为STL文件，然后导入Flow-3D，并将计算单位转换为计算所需要的厘米制。为了达到模拟结果与工程实际的高度吻合，应该尽量缩小网格划分，而网格数量的大幅增加势必会造成迭代时间的大幅延长。对两者进行综合权衡，模拟计算过程中选取渠道的计算长度为8.0m，高度为45cm，宽度为65cm，计算单元的网格为棱长1.5cm的正方体网格，因此整个计算区域可以划分为约500000个网格。

1.5 边界条件

Flow- 3D模拟计算过程中，需要按照水流入口边界进行渠道流量的设定，而对于计算域内的流体则需要利用N- S方程进行求解。因此，模型建立中需要设置合理的边界条件。如图1所示。将U型渠道的进口设定为流量进口条件，并以此为基础设置进口流量；将U型渠道的出口水流设置为自由流条件；由于渠道的侧壁以及渠底为水流和固体接触面，因此设定为无滑移壁面边界条件；上部的自由水面设置为对称边界条件。

2 计算结果分析

2.1 堰顶长度对水面线的影响

在U型渠道中采用斜坎平顶量水堰时，由于堰顶得到延长，量水堰部位的水流流态能够比较平稳过渡。研究中为了进一步探究不同量水堰堰顶长度对水流的影响，结合工程实际设计了15cm、20cm、30cm、40cm等四个不同的堰顶长度L2的取值，并利用上节构建的构建的模型对U渠道的水流流态进行数值模拟分析。结果显示，堰顶长度的变化对U型渠道内的水流流态影响不大，但是堰上水面线的变化比较显著。根据沿程水深计算结果绘制的水面线图如图2所示。由图可以更直观的看出堰上水面线的显著变化。堰顶长度越长，水面线的跌落就越平缓，当堰顶长度为15cm和20cm时水面线的变化最为平滑。

图2 不同堰顶长度下的纵剖面水面线

2.2 对佛汝德数的影响分析

利用上节构建的模型，对坡度为1∶200，流量为20.10L/s，压强为10cm时的佛汝德数进行计算，获得如图3所示的佛汝德数沿程变化曲线。由图可知，随着量水堰堰顶长度的增加，佛汝德数的最大值也呈现出逐渐增大的趋势，且佛汝德数的最大值均出现于量水堰的末端；随着量水堰堰顶长度的增加，U型渠道的临界水深位置呈现出逐渐后移的特征，且上下游的佛汝德数变化情况基本相同。由于U型渠道内的水流在跌落至量水堰前的佛汝德数已经大于1，因此，从佛汝德数的角度来看，上述各个堰顶长度的量水堰均满足测流要求。

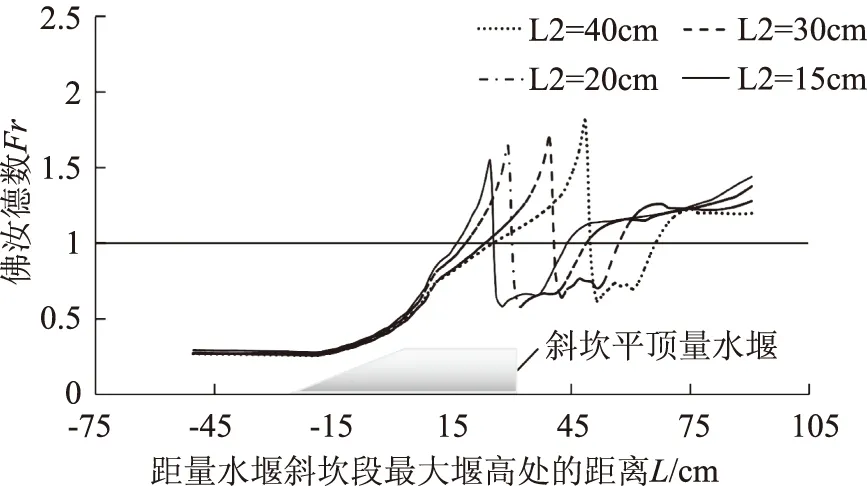
图3 不同工况下佛汝德数沿程变化曲线

2.3 水头损失影响分析

为了进一步研究量水堰的水力性能，对坡度为1∶200，流量为20.10L/s，压强为10cm时的U型渠道水头损失进行模拟计算，结果见表1。由表中的结果可知，如果U型渠道的渠底坡度较大，在相同流量条件下的流速也较大，因此渠道的水头也较大，而堰顶长度为15cm时的水头总损失占比最小，所以更适合在实际工程中应用。同时，相对于其他尺寸，还具有便于安装和节约材料的优势，建议在具体工程中采用。

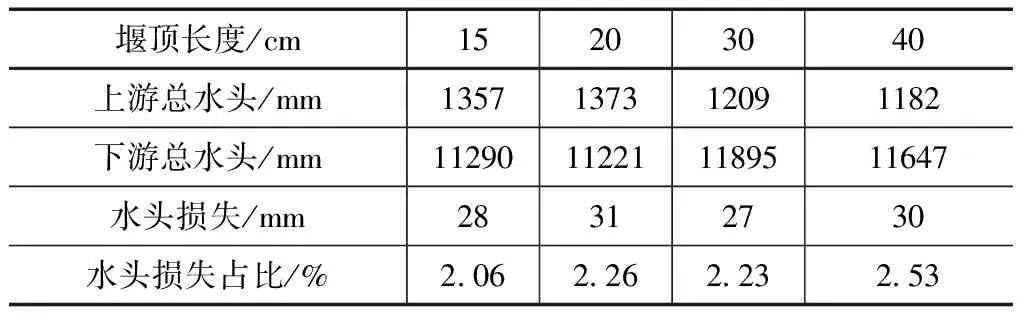
表1 水头损失计算结果

3 结论

针对U型渠道测流问题，利用FLOW- 3D软件对U型渠道四种不同堰顶水平段长度下的量水堰性能进行了对比分析，获得如下结论：

(1)堰顶长度的变化对水流流态影响不大，但对堰上水面线的影响比较显著，堰顶长度越长，水面线的跌落就越平缓，当堰顶长度为15cm和20cm时水面线的变化最为平滑。

(2)随着量水堰堰顶长度的增加，佛汝德数的最大值呈逐渐增大的趋势，且佛汝德数的最大值均出现于量水堰的末端；临界水深位置呈现出逐渐后移的变化特征。

(3)在高×宽=45cm×65cm计算模型下，堰顶长度为15cm时的水头总损失占比最小。