银河系光行差及其对天文参考架的影响∗

刘佳成 刘 牛

(南京大学天文与空间科学学院南京210023)

1 引言: 银河系光行差

众所周知由于光速是有限的, 观测者的运动(位置随时间的一阶变化)会导致天体的观测位置与真方向发生偏离, 这种观测效应称为光行差.类似的, 观测者运动的加速度(位置随时间的2阶变化)也会使天体的视运动速度发生变化, 反映在天球上, 就是天体自行发生了改变, 这种现象称为光行差漂移[1–2].

当前的基本天球参考系, 即国际天球参考系(International Celestial Reference System, ICRS)是以太阳系质心为坐标原点的准惯性参考系[3], 基本假设是坐标原点为静止或者做匀速直线运动, 并通过国际天球参考架(International Celestial Reference Frame, ICRF)得以实现[4].国际天球参考架第3代星表(ICRF3)已于2018年在奥地利维也纳召开的国际天文学联合会(International Astronomical Union, IAU)大会上得到通过.从2019年初开始, 天文观测所使用的基本天球参考系由ICRF3实现[5].为了实现惯性参考系, ICRF星表提供了一批由射电甚长基线干涉(Very Long Baseline Interferometer,VLBI)观测得到的河外源(包括星系、活动星系核等天体)的位置, 精度在亚毫角秒的水平.河外源最大的特点是距离我们非常遥远(至少Mpc量级), 由于观测精度的限制, 认为它们在天球上没有横向运动, 即自行为零(或者说自行极小, 在当时的观测精度下完全可以忽略)[6].根据该假设, 利用这些遥远河外源的不随时间变化的天球坐标, 就可以建立一个与历元无关的运动学无旋转的准惯性参考系(或者称为“空固参考系”).但是,ICRS的坐标原点, 即太阳系质心在银河系中的状态显然不是静止或匀速直线运动, 而是存在加速度的.根据上面关于光行差概念的描述, 太阳系质心的加速度将产生一个与河外源距离无关的视自行, 导致了实现天球参考架的基准点(即河外源)不再是静止的, 这个由太阳的加速度引起的观测效应被称为“长期光行差漂移”[7–9].近年来对这个新问题已经有一些研究, 例如通过VLBI观测拟合射电源的自行进而估计长期光行差效应[10–11],直接利用VLBI资料估计太阳的加速度[12–14], 再评估对地球自转参数的影响[15]等.

在银河系中, 太阳系质心的加速度主要由以下两部分运动组成: (1)太阳相对于本地静止标准(local standard of rest, LSR)的运动; (2) LSR相对于银河系中心的轨道运动.2006年, Kopeikin等[16]已经证明, 太阳相对于LSR的运动引起的光行差自行小于1µas·yr−1.这仅仅是第2项轨道运动引起效应的1/10, 因此可以忽略不计.基于以上的估算, 仅需要考虑LSR绕着银河系中心做圆轨道运动的加速度, 它的大小是常数, 方向随时间变化, 并指向银河系中心.由这个向心加速度引起的光行差漂移称为“银河系光行差”效应.描述这个效应的术语, 有“自行中的光行差”[8]、“长期光行差”[16]、“长期光行差漂移”[9]等; 也可以更精确地称为“银心光行差漂移”.到目前为止, 对该现象的名称和术语并没有官方的定义或推荐名[15].Titov[9]和Malkin[17]认为, 银河系光行差效应在高精度天体测量中需要考虑, 并且相应的VLBI数据处理软件也需要加入这一项[18].

在以太阳系质心为原点的参考系中观测天体, 假设t0时刻的真位置为p, 由于太阳系质心的运动, 在另一个时刻t, 这个天体的视位置p′为[15–16]:

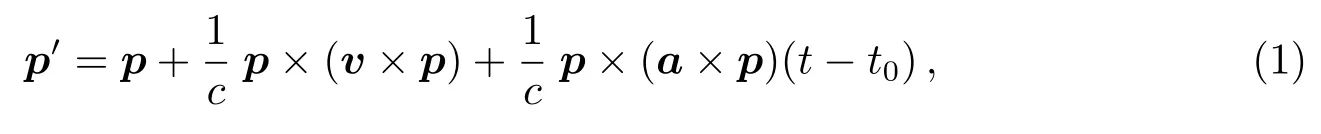
其中c是真空中的光速, v是太阳运动的速度, a是太阳运动的加速度, 速度的2阶以上导数的项已经忽略.如果忽略长期视差, (1)式的右边前两项是常数, 而第3项则是本文讨论的长期光行差漂移.在文献中, 通常也使用光行差矢量g = a/c来表征银河系光行差效应.假设太阳系质心仅仅绕着银河系中心旋转, 并且是圆轨道运动[8], 于是光行差矢量g可以简单写为:

其中ω0和V0分别是太阳系质心绕着银心旋转的角速度和线速度, R0是太阳到银心的距离.g0是从太阳系质心指向银心的单位矢量.矢量g的大小g称为光行差常数, 它的单位与自行相同, 为µas·yr−1.

在第2节中,将对银河系光行差的数学表达式和常数g的大小进行详细讨论.在第3和第4节中, 将介绍银河系光行差对河外源参考架和地球自转参数的系统影响.第5节是对光学和射电参考架连接的讨论.最后一节是对银河系光行差效应的总结和展望.

2 银河系光行差的表达式

2.1 球面向量场的矢量球谐函数展开

严格描述银河系光行差引起的河外源视自行需要用到矢量球谐函数[19–20].单位球面上的矢量场V(α,δ)可以利用矢量球谐函数进行展开为赤经和赤纬两个分量(其中α和δ分别表示赤经和赤纬):

其中eα和eδ是球面上某一点(α,δ)的切平面上沿着赤经和赤纬增加方向的单位矢量;Tlm和Slm是两类彼此正交的函数, 它们是基于球谐函数而构造的, 作为矢量场展开的正交基底; tlm和slm是系数; 下标l和m是展开的阶数和次数.通常在计算时, 将阶数截断至lmax, 通过矢量球谐函数的系数来考察矢量场的几何和分布特征.随着lmax的增加, 可以研究矢量场在更小范围内的结构和细节.而最低阶的矢量球谐函数(l =1,2)则显示的是矢量场的全局特征或者“长波”特征.

银河系光行差对应于最简单的矢量场, 只包含最低阶的矢量球谐函数, 并且在Tlm基函数上没有投影分量(即tlm= 0).若太阳系的加速度矢量(指向银心) g在赤道坐标系中为g =(g1,g2,g3), 则根据它引起的河外天体的速度场可以写为:

其中u = (cos α cos δ,sin α cos δ,sin δ)是天球上某一河外天体(α,δ)方向上的单位矢量.将速度场vg投影到天球上以该天体位置为切点的切平面上, 就可以得到该河外天体的自行表达式:

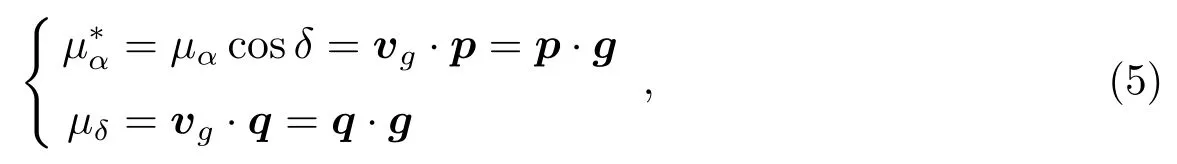
其中p=(− sin α,cos α,0)和q =(− cos α sin δ,− sin α sin δ,sin δ)分别是切平面上沿赤经和赤纬增加方向的单位矢量.很显然(p,q,u)是一组互相垂直的正交单位矢量.将上式展开, 得到银河系光行差引起的自行(简称银河系光行差自行)的表达式:

这样, 给定光行差矢量g以及天球上河外源的赤经和赤纬, 就可以通过(6)式求出光行差引起的视自行.

2.2 银河系光行差常数的估计值

理论上, 太阳系的加速度应当指向银河系中心: α0266.4◦,δ0−28.4◦[21–22], 或者ℓ=0,b=0, 其中ℓ和b分别表示银经和银纬.为了得到加速度在赤道坐标系下的3个分量, 还需要计算银河系光行差常数g, 它决定了它引起的河外天体视自行的大小, 因此是一个十分关键的参数.确定g的值有多种方法, 比较简单的方法是利用太阳绕银河系中心的圆轨道运动的(2)式.根据最新的研究, 取太阳的银心距R0=8.2 kpc, 圆轨道运动的角速度为ω0=29.5 km·s−1·kpc−1(6.22 mas·yr−1)[23].可以计算得到

采用上述值, 计算得到g在赤道坐标系中的分量为

根据目前参数R0和ω0的精度, 光行差常数g的误差水平为5%–10%[17].

除了理论上的估计, 2011年Titov等[10]利用VLBI观测的河外射电源位置序列, 线性拟合了555颗河外源的自行.最终得到的光行差常数为g =6.4±1.5µas·yr−1, 指向的方向为α=263 ± 11◦、δ = 20 ± 12◦, 与银心(半人马座A)的方向 α = 265◦, δ = −29◦之间的角距离约为10◦.进一步, Titov等[11]在2013年使用了新的观测资料, 改进了数据的筛选和拟合方法, 得到了类似的结果(文章中的DR (Dipole-Rotation) solution):g ≃ 6.2 ± 1.3µas·yr−1, 与银心的角距离约为7◦, 结果的精度相比2011年(文献[10])改进了约20%.2018年, Titov和Kr>sn又利用地球尺度因子全局解的方法[24], 得到了独立于河外射电源自行的光行差常数: g5.2±0.2µas·yr−1, 与银心的角距离为20◦.2012年,Xu等[13]则是从另一个角度考虑太阳系的加速度, 将太阳系质心加速度作为一个全局参数, 利用VLBI软件Calc/Solve中的偏导数工具, 从资料中直接解算出加速度的值, 此方法与银河系的结构和运动学模型无关.该研究工作得到的结果显示, 太阳系质心加速度垂直于银道面的分量非常明显, 与向心加速度量级相同, 总加速度的方向与银盘面的夹角达到33◦, 目前在其他理论中并没有预计到[13].2018年, Liu等[25]在分析了几个VLBI数据中心的河外源位置序列后, 也得出光行差常数约为5µas·yr−1, 方向大致指向银心的结论.因此在后续的介绍中, 我们就选定

并认为它指向银河系的中心.表1中列出了不同文献中计算得到的光行差常数g的大小(第1行)和方向(第2和第3行), 最后一行是各个文献得到的太阳系加速度与银河系中心方向的夹角.

3 银河系光行差对河外源参考架的影响

银河系光行差自行呈现非常规则的几何特征, 在很多文献中都给出了几何图示[16–17]: 在天球上, 每一颗河外源都是沿着连接反银心和银心的大圆弧运动, 视自行的大小仅与河外源的位置有关, 更准确说, 是与河外源和银心之间的角距离ζ有关:

由此可见, 在垂直于银心−反银心连线的大圆上(此时ζ =90◦), 河外源的视自行最大, 其值就是g =5.02µas·yr−1; 在银心和反银心的位置(此时ζ =0◦), 河外源不受长期光行差的影响, 视自行为零.根据最新的ICRF3中303颗定义源的位置, 图1给出了银河系光行差引起的视自行分布, 它们的大小可以根据(6)或(10)式计算得到.

表1 文献中对银河系光行差常数的估计aTable 1 The estimates of the Galactic aberration parameters from recent publicationsa

图1 ICRF3中定义源的位置以及银河系光行差引起的视自行分布Fig.1 The defining sources in the ICRF3 and the distribution of apparent proper motions resulting from the Galactic aberration effect

一般来说, 天球参考架的3个空间坐标轴是彼此正交的, 不同的参考系之间可以用一个整体的刚性旋转来描述.由于银河系光行差的影响, 原本自行为零的河外源产生了如上图所示的视运动, 于是它们实现的天球参考架ICRS将发生一个小角度的刚性旋转, 将旋转后的参考系记为ICRS′, 它们的关系可以写为[15,28]:

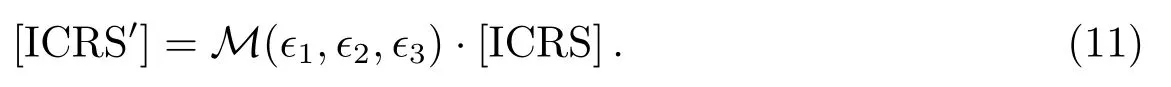
式中3×3矩阵M的形式为:

其中

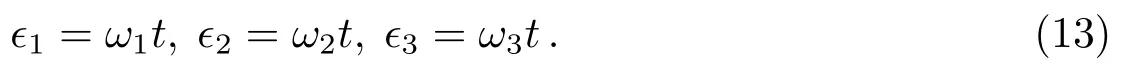
其中, ϵ1,2,3是参考系ICRS绕着3个坐标轴转过的角度, 而ω1,2,3是由于河外源的自行引起的参考架的旋转速率.在已知一批河外源自行的情况下, ω1,2,3可以通过以下的公式拟合得到[29]:

这里(14)式和(6)式的含义完全不同: (6)式用来计算银河系光行差大小, 而(14)式则是在已知自行大小的情况下, 拟合它们引起的参考架的整体旋转量的公式.Liu等[15]在2012年的工作中给出了根据ICRF1和ICRF2的射电源分布求得的参考架旋转量.其主要的结论是: 银河系光行差引起的参考架整体旋转与河外源分布的均匀程度密切相关, 而与源的数量没有直接关系.源的分布越均匀, 银河系光行差引起的参考架整体旋转越小.根据Liu等[15]2012年工作中的表1, ICRF1中的212颗定义源分布主要集中在北半球, 相应的旋转速率为(1.10±0.14)µas·yr−1, 而ICRF1中所有的608个源的分布相对更均匀, 相应的光行差引起的旋转量只有(0.22±0.09)µas·yr−1.另外, 如果使用随机的均匀分布, 则银河系光行差引起的参考架旋转完全可以忽略.

银河系光行差是由太阳系质心圆轨道运动的向心加速度引起的, 因此在银道坐标系中[30–33], 能更清楚地反映光行差自行的几何特征, 计算表达式也会变得更为简洁.在银道坐标系(坐标原点为太阳系质心、X轴指向银河系中心、Z轴指向北银极)中, 若已知河外源的银经ℓ和银纬b, 则银河系光行差自行的表达式为:

从上面的公式也可以得出在银心和反银心方向上的河外源视自行为零, 而最大的视自行出现在垂直于银心和反银心的大圆上(与(10)式的结论相同).在银道坐标系中, 仍然利用ICRF1和ICRF2中的射电源拟合参考架的整体旋转, 可以发现绕着X轴的旋转永远为零, 而旋转矢量ω必定垂直于银道坐标系的X轴, 但大小和方向仍然与河外源的分布有密切的关系[15].

4 银河系光行差对地球自转参数的影响

根据IAU和国际地球自转服务(International Earth Rotation and Reference Systems Service, IERS)的推荐, 用天球中间极(Celestial Intermediate Pole, CIP)在地心天球参考架(Geocentric Celestial Reference System, GCRS)[34]中的位置来描述地球自转轴的指向[35–36]: 即用参数X和Y (它们分别表示CIP在GCRS中的方向余弦)随时间的变化来直观描述岁差和章动[37–39]; 描述地球绕着CIP旋转则使用地球自转角(Earth Rotation Angle, ERA)[40].显然, 地球自转参数X、Y 以及ERA与所处的参考架密切相关.由于银河系光行差效应, GCRS会有缓慢的转动, 在这个转动的参考系中描述地球自转, 相应的参数必然也会受到系统的影响.

根据Malkin在2011年的研究工作[12], 由于在VLBI数据处理中引入银河系光行差效应, 得到的岁差速率的修正值为:

Liu等[15]在2012年的工作计算了银河系光行差引起的天球参考架旋转速率ω1,2,3, 依据地球参考架和天球参考架的转换关系, 得到地球自转参数修正量的理论表达式:

银河系光行差在未来的30 yr, 对天球参考架和地球岁差参数的影响累积可以达到几十微角秒的量级, 这比它们本身精度水平要大得多.因此, 在未来的VLBI资料处理中,必须考虑河外源的视自行, 以将这一项的影响消除[41].

5 银河系光行差对射电与光学参考架连接的影响

上面的叙述主要讨论了银河系光行差对射电波段的ICRF的系统影响.从最普遍的光学观测角度来说, 河外射电源的视星等一般都在17等以上, 因此在光学波段观测它们很困难.为了使ICRF在其他波段上更加具有实用性, 必须给出其在光学波段上的实现方法.显然, 无论是在光学还是在射电波段上, 国际天球参考架的含义应当是一样的: 即是由遥远的河外源实现的惯性框架.

上世纪90年代发射的第1代天体测量卫星依巴谷(Hipparcos)为实现高精度光学天文参考架提供了良好的观测资料.Hipparcos卫星提供了亮于11等的恒星的位置、自行以及视差, 典型的精度为1 mas和1 mas·yr−1[4,42].由于Hipparcos大角度空间天体测量的特征, Hipparcos星表天然形成一个与其测量精度相符的光学参考架.然而Hipparcos参考架(简称HCRF)并不能与当时的第1代ICRF直接连接, 原因是Hipparcos的极限星等(约为13等)不足以观测到足够多暗弱的河外源.为了实现两个波段参考架的连接,使用了诸如射电星、河外射电源的光学照相底片观测、地球自转参数等多种间接手段[4,43].最终, 两个参考架连接的精度为0.6 mas和0.25 mas·yr−1.需要强调的是, 概念上基于VLBI观测的ICRF和基于空间光学观测的HCRF, 它们的坐标轴指向是完全一致的, 并且没有任何的相对旋转.因此上面的两个数字更严格的含义为: 前者说明两个参考架坐标轴之间的角度差为(0±0.6)mas, 而后者说明坐标轴之间的相互旋转速率为(0±0.25)mas·yr−1, 连接的误差在几百微角秒的水平.很显然, 在Hipparcos时代, 微角秒量级的银河系光行差((2)式)是完全可以忽略的.

5.1 Gaia卫星对河外源的天体测量观测以及第3代国际天球参考架ICRF3

2013年底, 欧洲空间局发射了第2代天体测量卫星Gaia[44], 至今已经发布了第2批观测资料(Gaia DR2),包含了超过17亿个天体的位置、自行、视差以及测光数据[45].Gaia的天体测量精度相比于Hipparcos有了极大提高.Gaia的极限星等达到21等以上, 可以在全天区观测到足够多的河外源(星等主要分布在18–20等), Gaia DR2发布的河外源位置误差的中位数大约为0.4 mas[46].Gaia观测模式与Hipparcos类似, 不依赖于先验的参考架, 从而可以独立地构建一个光学波段上刚性的惯性参考架.与Hipparcos参考架不同的是, Gaia可以提供数十万颗河外源的天体测量信息, 因此是基于遥远河外天体的参考架(HCRF是基于恒星), 并且河外源的数目比VLBI观测得到的ICRF河外源多了约3个量级[47].

根据Mignard等[47]在2018年关于Gaia-CRF2 (基于Gaia DR2数据的天球参考架)的研究, 当前最好的光学和射电参考架(即Gaia-CRF2和ICRF3)的坐标轴指向偏差为(0±30)µas.更重要的是, Gaia DR2数据首次给出了约50万颗河外源的自行.将这些自行拟合到(6)式, 并不能还原理想的太阳系绕银河系中心旋转的加速度, 从中体现出Gaia在大尺度上存在着大约10µas·yr−1量级的系统差, 这可能与Gaia在暗端观测精度下降导致观测误差增大, 以及忽略了河外源在射电和光学波段的结构[48–50], 从而导致系统误差没有扣除有关.

在2018年的第30届IAU大会上, ICRF3被采纳作为基本天球参考架, 以替代其前身ICRF1 (608颗源)[51]和ICRF2 (3414颗源)[52].ICRF3除了传统的S/X波段(2.3和8.4 GHz), 还有更高频波段的数据: K波段(24 GHz)和X/Ka波段(8.4/32 GHz)[5].ICRF3总共包含4536颗射电源, 在S/X波段, 选出了303颗全天均匀分布的定义源, 它们观测历史丰富, 位置稳定, 用来定义参考架的坐标轴指向.在ICRF3的建立过程中, 考虑了银河系光行差效应.此时在没有改正银河系光行差效应的情况下, VLBI观测解算得到的射电源位置不再与历元无关, 而是相对于其观测的平均历元而言的.每一个射电源的位置历元几乎都是不同的.而进行银河系光行差效应改正之后, 所有射电源的VLBI位置是相对某一特定的改正历元而言的.假设银河系光行差矢量g指向银心方向, 此时的待定参数为银河系光行差常数g.为了确定g的大小, ICRF3工作组在3−10µas·yr−1之间选取了一系列g值进行VLBI解算.银河系光行差的改正历元选与Gaia DR2相同, 为J2015.5, 以便与射电源的Gaia DR2位置进行比较.如图2所示, 当g的值在5−6µas·yr−1之间时, 射电源的VLBI位置相对于Gaia DR2位置的区域系统偏差最小.由此, 最终确定了银河系光行差的大小为

在精度要求非常高的情况下, 应当以J2015.5为基本历元, 加上用(6)式计算的赤经和赤纬自行, 而其中的银河系光行差常数g取(18)式中的值.因为考虑了银河系光行差自行,ICRF3给出的河外源位置是与历元有关的, 这和ICRF1[51]和ICRF2[52]的情况有所不同.

图2 VLBI解算得到的射电源位置相对于Gaia DR2位置的区域系统差随着银河系光行差常数g的变化.其中, g1、g2和g3表示的是沿坐标轴X、Y、Z的偶极形变量.Fig.2 The glide between the VLBI and the Gaia DR2 positions as a function of the Galactic aberration constant g.The parameters g1, g2, and g3 stand for the dipolar deformation along the X-, Y-, and Z-axis, respectively.

5.2 射电和光学参考架的连接方法

近5 yr来, 光学和射电参考架有了重大的革新, 观测的河外源数量和精度大幅提高,银河系光行差效应的引入也使得参考架的概念发生了改变.ICRF3和Gaia天球参考架的连接方法也成为基本天文学亟待考虑的重要问题之一[41,53].

Gaia和ICRF工作组提出, 在Gaia的观测完成之后, 仍以VLBI观测得到的射电波段的参考架ICRF为基本天球参考架, 把光学波段的Gaia参考架向其进行连接, 从而使两者的坐标轴完全一致.具体来说, 仍然承认ICRF3中的数千个河外射电源没有自行, 因此是一个理想的空固惯性参考架.另一方面, Gaia作为空间大角度天体测量卫星, 能获得一个与其观测精度相符的参考系, 这应该被认为是一个中间参考系(称为AGIS参考系[54]), 它与ICRF之间仍然存在着微小的指向差异和相互旋转.

在中间参考架AGIS中, 河外源位置与Gaia观测的中间历元T联系[55], 而河外源自行至少由以下4个部分组成: (1) AGIS相对惯性系旋转引起的自行; (2)由银河系光行差引起的自行; (3)由源结构引起的自行; (4)观测误差引起的自行, 即:

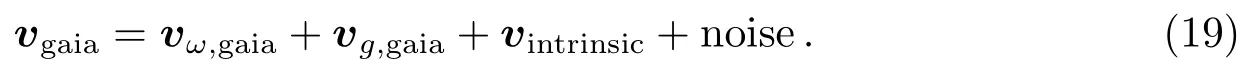
其中前两项是系统项, 下标ω和g分别表示整体旋转和银河系光行差效应.第(3)项源结构效应可以通过长期的观测去掉那些结构明显的源, 只保留结构稳定的源, 而第(4)项的分布是随机的, 对参考架整体的指向和旋转没有影响, 仅仅影响连接的精度, 因此后两个效应在下面的讨论中暂不考虑.

在把Gaia连接到ICRF的过程中, 第1步利用Gaia观测的数十万颗河外源的自行拟合矢量g及ω (根据Liu等[25]在2018年的估算, 它们的精度大约为几十µas·yr−1), 进而把这两个系统效应从河外源的自行中去除.这样, 改正过的自行从整体上看将没有剩余旋转和光行差效应.第2步利用Gaia和ICRF共同源(约4000颗源), 在某个历元T确定两个参考架的指向偏差ϵ(T), 将所有Gaia观测的河外源位置(也包括恒星), 依照矢量ϵ(T)生成的旋转进行修正, 以连接到VLBI框架上去.

Liu等[55]考虑了两个波段河外源的自行(正如从AGIS出发构建Gaia惯性参考架的做法), 进而提出了基于新天体测量模型的参考架连接方法.在这项工作中, 由VLBI观测的河外源速度和(20)式对应, 即在射电波段也考虑上述(1)–(4)项速度的组成:

而不再将射电波段的河外源当成是静止不动的.这在微角秒精度的天体测量中是更合理的, 并且光学和射电波段的河外源运动模型也应当是一致的.在考虑河外源运动的情况下, 当前观测得到的VLBI参考架也应当认为是一个中间参考系, 其中缓慢的自转ω以及银河系光行差矢量g应当通过VLBI观测的数千颗源的自行计算得到, 然后利用ω和g (它们的精度大约为1µas·yr−1)将中间参考系的剩余旋转和银河系光行差消除, 这样得到惯性无旋转的VLBI框架.最后, 修正的VLBI框架和Gaia框架可以在某个历元进行连接,即消除两者在指向上的差别.无论使用哪种连接方法, 在J2015.5 (目前Gaia观测的中间历元), Gaia和VLBI参考架之间的指向差大约为100µas, 精度约为20µas.

6 总结和展望

银河系光行差效应源于太阳系绕银河系中心旋转的向心加速度, 造成天球上所有的天体都会产生一个额外的指向银心的视自行(即银河系光行差自行), 最大值大约为5µas·yr−1, 仅仅依赖于河外源和银心之间的角距离(见(10)式).

在微角秒精度天体测量时代, 银河系光行差将显得愈发重要: 遥远的河外源作为实现参考系的基准, 不再是固定不动的, 至少银河系光行差是其中的一个重要系统项.银河系光行差会造成国际天球参考架随时间的缓慢旋转, 量级大约为1µas·yr−1, 且与源的分布有关.除了整体旋转, 银河系光行差引起的河外源参考架扭曲还有待进一步研究.银河系光行差对VLBI测量得到的地球自转参数的系统影响反映在岁差速率上大约为1µas·yr−1.这虽是一个小量, 但随着时间的积累, 在未来建立新的岁差模型时需要加以考虑.在Gaia和VLBI参考架的连接工作中, 银河系光行差也是需要特别关注的一个系统效应, ICRF3和Gaia已成立相关工作组对其进行专门的讨论和研究.

从实测上看, 银河系光行差已经可以从VLBI数据处理中获得, 但是各种方法获得的测量值仍存在不小的差异.Gaia由于本身的系统差, 用第2批数据的河外源资料尚无法可靠地检测出银河系光行差效应.存在这些不相符的原因, 除了观测本身存在误差(比银河系光行差本身的量级大很多)以外, 更重要的因素是对河外源本身在光学和射电波段的结构还了解甚少[56].2019年, Xu等[57]利用VLBI闭合时延量, 给出了源的结构指数, 这将对银河系光行差以及参考架的建立和连接起到重要作用.

银河系内的恒星也会受银河系光行差的系统影响.Kovalevsky[8]和Liu等[58]的研究指出, 恒星的光行差自行除了和太阳的加速度有关, 还与恒星本身绕银心的轨道加速度有关.在银心附近, 光行差效应将被放大至100µas·yr−1, 而其他区域的量级仅仅在1µas·yr−1.根据Gaia的观测, 银心区域由于消光以及距离较远, 恒星的天体测量误差远比100µas·yr−1大, 因此银河系光行差对恒星自行产生的系统影响目前并不需要考虑.

从银河系光行差形成的原理来看, 只要将参考系的原点从太阳系质心平移到银河系中心, 参考系的原点就不再有额外的加速度, 文中讨论的光行差效应自然也就消除了[8].改变参考系的原点需要我们对银河系中所有天体的运动情况给出精确的观测, 同时建立全局和局部的引力场的精确理论模型(就像我们对太阳系的了解程度一样)[59].然而, 即使在Gaia任务结束时, 也不可能做到这一点, 因此将参考系的原点移到银河系中心以消除银河系光行差效应是不现实的.