定机移船码头的靠船桩系统计算方法
冯建国,李存兴,王君辉
(中交第二航务工程勘察设计院有限公司,湖北 武汉 430060)
随着社会经济的不断发展,东南亚等国家对电力的需求越来越大,大量的电厂需要兴建。由于该区域潮差不大,悬链斗式连续卸船机在该区域广泛应用。该类型码头由固定装卸平台上的悬链斗卸船机、设置在移船平台上的移船设备及设置在码头前沿的靠船导向系统组成。码头作业过程可简述为以下过程:船舶靠泊完成后,移船平台上的牵引小车将船舶牵引至合适位置,悬链斗开始作业卸煤,当卸煤作业进行到一定程度后,再次启动牵引小车使船舶沿靠船导向系统移动至适当位置,使悬链斗卸煤效率保持最大化,如此反复,直至整船煤全部卸完,船舶离港。该类型码头卸煤时船舶移动而卸船设备不动,所以可简称为定机移船码头。
传统的“定船移机”码头,船舶靠泊后位置是固定的,通过移动装卸设备来完成装卸作业,平台通常为常规的高桩梁板结构或高桩墩式结构,结构受力明确,设计理论成熟。而柔性靠船桩设计规范[1]主要针对护舷在外、靠船桩在内的情形,而且靠船桩系统与码头平台往往是脱离的,其受力模式不适应于定机移船码头。而本文所指定机移船码头水工结构主要由卸船机基础墩台、移船设备行走平台及设置在二者前沿的靠船桩组成,平台前沿的靠船导向则由靠泊导向钢管桩及橡胶护舷两部分组成。靠泊导向钢管桩之间设有水平联系撑,形成桩排,移船时,船舶与钢管桩直接接触而不与橡胶护舷接触,从而避免了橡胶护舷在移船过程中被撕裂的可能,同时移船时船舶与钢管桩发生摩擦,摩擦系数较小有利于船舶移动。钢管桩在外侧,护舷在中间,码头平台在内侧,其受力较为复杂,没有现成的规范和手册可供参考,如何确定靠船桩排的尺寸,将关系到整个结构的安全性和经济性,因此需对其受力特点进行仔细分析和论证。本文主要论述靠船导向桩排的计算方法和特点。
1 靠船导向桩排的工作过程
船舶靠泊时,首先接触码头前沿所设靠船导向桩排,靠船桩自身将发生变形,同时设于桩顶的橡胶护舷也随之被压缩,靠船过程结束时,船舶速度降为0,船舶靠泊的动能转化为靠船桩和护舷系统的势能。在整个靠泊过程中,靠船桩排起到传力的功能,并吸收部分能量,最终船舶靠泊能量由护舷和靠船桩共同吸收。
2 靠船桩计算模型简化
2.1 系统作用过程基本假设
2.1.1靠船墩台不产生变形吸能的假设
由于墩台刚度远远大于靠船桩,为简化计算,靠船墩台简化为固定支点,忽略船舶靠泊过程中墩台变形对靠泊能的影响。墩台自身变形吸能,对整个系统的影响较小,作为安全储备。
2.1.2船体本身不产生变形吸能的假设
为简化计算,在靠泊过程中船舶自身变形引起的吸能不计。
定机移船码头靠船桩布置见图1。
2.1.3橡胶护舷的基本假设
根据护舷的变形反力曲线特性,将橡胶护舷的压缩过程简化为一个理想弹塑性体,见图2。


图2 橡胶护舷变形过程的简化
护舷变形22.5%之前按照理想弹性体考虑,反力与变形成正比,护舷吸能与变形成平方比关系增加。护舷变形22.5%之后按照理想塑性体考虑,变形增加,反力不变,护舷吸能与变形成线性关系增加。计算后,应核实最终护舷变形量不超过52.5%。
2.1.4桩基计算采用假想嵌固点
桩土作用复杂,张铁峰等[2]给出了靠船桩入土较短、桩端为铰接时的简化计算,当覆盖层较差、持力层埋深较深、桩基入土长度较长时,桩基受弯长度采用假想嵌固点[3]进行简化计算。
2.2 作用过程简化
靠船桩根据上述假定,最终简化为一端固定一端弹性支撑的单跨超静定梁,见图3。

图3 靠泊过程受力计算
靠船过程分为3个阶段:
1)第1阶段,从船舶接触靠船桩开始,钢管桩发生变形,变形达到安装缝隙(假定1 cm),到钢管桩接触到护舷,护舷变形为0%(尚未产生弹性变形)。
2)第2阶段,从钢管桩接触到护舷开始,到护舷变形达到22.5%(弹性变形达到峰值),此时护舷反力已经达到最大。
3)第3阶段,从护舷变形达到22.5%开始(进入简化塑性变形阶段,护舷反力不增加),到船舶靠泊能量全部被吸收为止(护舷变形< 51.5%)。
2.3 计算受力过程分析
假设撞击点距离嵌固点高度为h,护舷点距离嵌固点高度为H,护舷最大反力为Rx,3个阶段护舷点的位移分别为x0、x1、x2,撞击点在3个阶段结束时的反力分别为F0、F1、F2,撞击点的位移分别为y0、y1、y2。受力计算简图见图3,桩身受力分解见图4,根据力学基本原理[4-5]可知:
第1阶段末,撞击点反力F0,护舷点反力R=0,撞击点位移y0和护舷点位移x0分别计算如下:
(1)
(2)
第2阶段末,撞击点反力F1,护舷点反力R=Rx,撞击点位移y1和护舷点位移x1分别计算如下:
(3)
(4)
第3阶段末,撞击点反力F2,护舷点反力R=Rx,撞击点位移y2和护舷点位移x2分别计算如下:
(5)
(6)

图4 靠泊过程桩身受力分解
2.4 系统能量分析
根据能量守恒定律,一个系统的能量变化仅与系统的初始状态及终止状态有关,而与过程无关,故计算中可忽略相对复杂的中间过程,而仅讨论几个阶段过程的初始状态和终止状态。
靠泊过程3个阶段外力对应的力-位移关系分析见图5。其中撞击点压力-位移关系,见图5a),图中折线所包含的面积Ec为撞击外力做功,即船舶靠泊能;护舷点反力-位移关系见图5b),图中折线所包含的面积Er为护舷反力做功,即橡胶护舷吸能。

图5 靠泊过程力-位移关系
整个过程钢管桩吸能:
(7)
整个过程橡胶护舷吸能:
(8)
船舶的靠泊能量:
(9)
桩底的最大弯矩:
M=F2h-RxH
(10)
桩身最大应力:
(11)
根据力和位移的对应关系,可以得到船舶撞击过程的动能,船舶动能等于桩基变形势能和护舷变形的势能之和,其中船舶撞击能量可以计算,也可以写成下式进行验算:
Ec=Es+Er
(12)
船舶撞击能可以通过规范公式计算:
(13)
式中:EI为桩身刚度;W为桩的抗弯模量;vn为船舶靠泊的法向速度。
在式(1)~(11)中,有F0、F1、F2、x2、y0、y1、y2、Es、Er、M、σ共11个未知数,x0假定为1 cm,拟定护舷之后,x1可由护舷高度×22.5%+1 cm计算,护舷最大反力Rx也为已知,Ec=E0。上述过程11个未知数可以11个方程联合求解。
如果最终结果x2橡胶护舷的变形大于22.5%且不超过51.5%,且钢管桩变形不超过允许应力,则整个系统设计是可行的。
3 工程实例
为进一步了解该结构形式的结构特点,本文选取4个具有代表性的工程实例做进一步分析阐述。
所选取的4个工程均位于印尼,码头装卸工艺均采用悬链斗式连续式卸船工艺,工程的设计基本资料见表1。
按照本文的计算方法计算,计算基本参数见表2。
根据本文所列公式(1)~(11)进行计算求解,结果见表3。

表1 码头基本设计参数

表2 计算基本参数
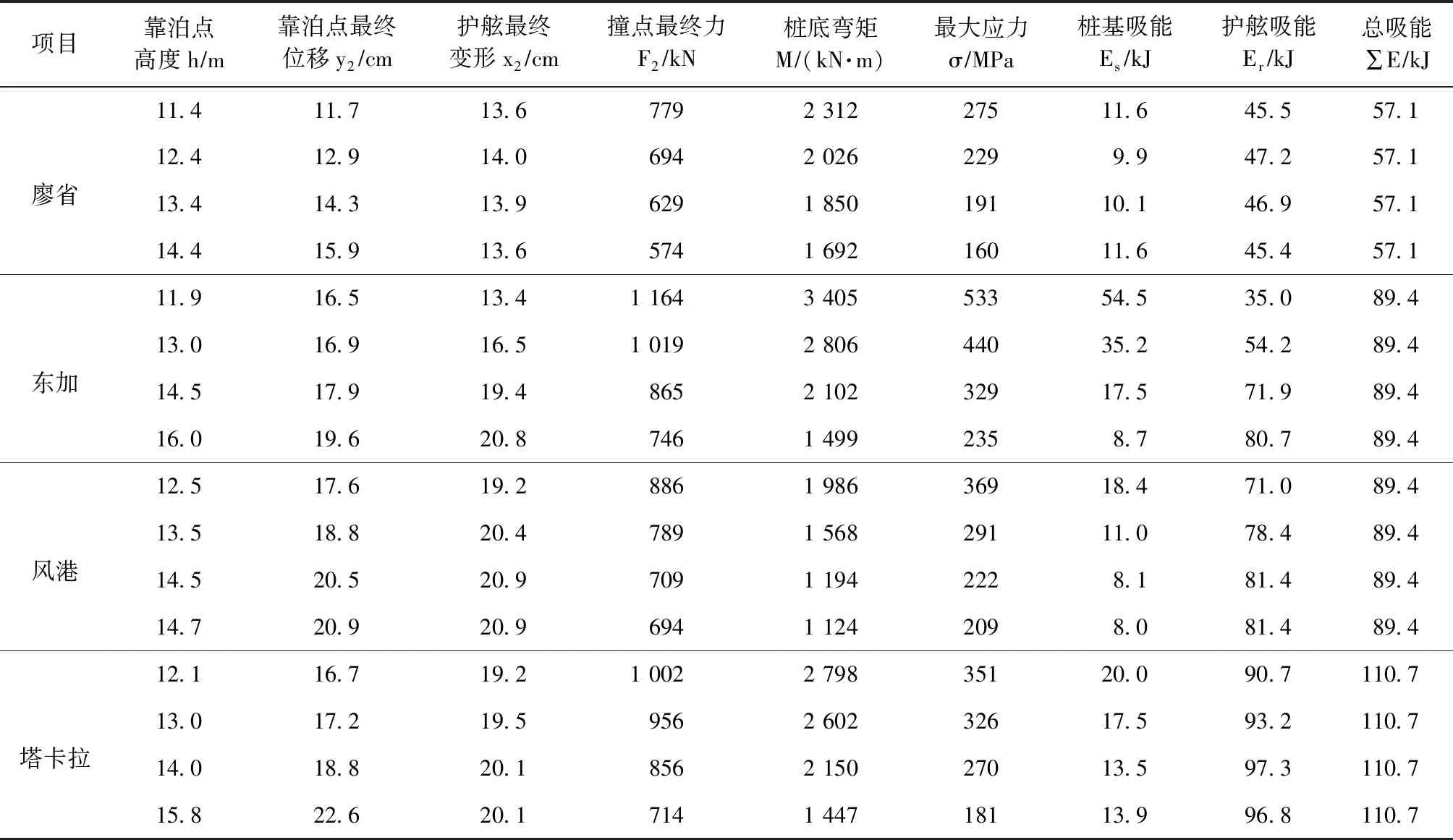
表3 主要计算结果
经复核,对于廖省和塔卡拉项目的大部分工况,选用高强度钢材强度基本满足要求。同时护舷点的变位满足护舷压缩变位的假设,计算方法是可行的。对东加和风港项目在低水位满载靠泊时不满足,如果不考虑钢横撑传递到其他靠船桩来分担吸能,也不考虑船舶自身变形的吸能,则需要允许钢管进入塑性状态。
4 结语
1)通过工程实例中码头结构计算可知,当船舶的靠船速度一定时,撞击点越靠近嵌固点则桩身内力值越大,吸能比例越大,桩径和壁厚加大,经济性差;反之,撞击点越靠近护舷布置位置,则桩身内力值最小,吸能比例最小,桩径和壁厚最小,最具经济性。故实际工程应用中,应注意分析各个有可能的撞击点,受力范围过大后,则不具经济性。
2)靠船排桩可适度扩大船舶撞击作用点范围,在强度允许的范围内,充分利用钢管桩变位吸能,减小护舷布置范围,相应减小墩台所受的护舷反力,从而降低码头造价。
3)本文没有考虑船舶自身变形和码头变形对系统吸能的分担,也没有考虑其他靠船桩对系统吸能的分担,计算结果偏保守。如果需要考虑橡胶护舷和钢管桩之外因素来分担吸能,则该靠船系统的计算理论有待进一步研究。

