航空复合材料加筋板压缩屈曲及后屈曲力学性能
高志刚,冯 宇,马斌麟,杜 旭,宋雨键
(空军工程大学 航空工程学院,西安 710038)
航空复合材料具有质量轻、可设计性强、抗热冲击等优点,然而,复合材料通常以薄壁结构的形式出现,采用加筋板能够较大地增强结构的整体刚度,提高层合板的结构效能[1],因此航空复合材料加筋板在现代飞机结构中得到了越来越广泛的应用,例如机身蒙皮、隔框、机翼和尾翼的翼面加筋板等[2-3]。复合材料加筋板在服役期间承受的载荷有多种形式,比如压缩、剪切、压剪组合等,其中轴向压缩载荷是服役过程中最常见的载荷形式之一。在轴向压缩载荷作用下,常见的失效模式为局部屈曲失稳,在发生屈曲失稳后并不会迅速破坏,通常表现出良好的后屈曲承载能力[4],但由于结构的后屈曲路径具有几何非线性的特点,其理论和应用一直是一个难题[5],因此研究复合材料加筋板在轴向压缩载荷下的屈曲及后屈曲能力对飞机的飞行使用安全有重要意义。
国内外学者们采用理论、实验和数值仿真方法对复合材料加筋板在轴压载荷作用下的屈曲和后屈曲力学性能进行了一系列的研究。宋刚等[5]研究了复合材料加筋板翼面结构稳定性问题,分析了加筋板在压缩载荷作用下的稳定性安全裕度;田秀云等[6]采用有限元素法,基于虚功原理,建立了加筋板结构的非线性屈曲平衡方程,并应用方程分析了若干算例,分析效果较好;于振波[7]研究了基于理想边界条件的复合材料平板蒙皮局部压缩屈曲计算方法在复合材料帽形加筋壁板蒙皮局部压缩屈曲计算中的适用性,并采用刚度等效的方法对基于理想边界条件的复合材料平板压缩屈曲计算方法进行了修正;Engelstad等[8]提出了渐进失效分析方法对复合材料层合板的后屈曲响应特性进行分析;李乐坤等[9]采用特征值分析法和改进的Risk分析法,引入Hashin实效准则及胶层实效准则对复合材料加筋壁板的屈曲和后屈曲过程进行了模拟与分析;Kong等[10]和Knight等[11]对整体成型加筋板在轴压载荷作用下的后屈曲及失效过程进行了研究,由于加筋板整体成型的特殊加工工艺,在破坏模式中没有出现壁板和筋条的脱粘分离现象;冯宇等[12]开展了航空复合材料加筋板压缩实验,得到了复合材料加筋板的屈曲载荷、破坏载荷及破坏模式;Kong等[13]、SHI等[14]和王平安等[15]开展了复合材料加筋板在压缩载荷及剪切载荷下的实验研究,结果表明复合材料加筋板在压缩载荷及剪切载荷下都会出现屈曲失稳现象,失稳之后仍具有较强的承载能力,即后屈曲承载能力;刘从玉等[16]利用非线性有限元的方法对复合材料加筋板在压缩载荷下的屈曲平衡路径和破坏过程进行了研究;赵维涛等[17]基于Abaqus软件,利用渐进失效分析方法对复合材料加筋板极限承载能力进行预测;孙斌等[18]应用有限元的方法对复合材料加筋板在受到轴压作用后的屈曲实效表征以及载荷传递机制进行了研究;Guo等[19]研究加筋板在压缩载荷下的屈曲和后屈曲过程,应用板单元模拟壁板,梁单元模拟筋条,有限元计算结果与实验结果的误差在± 10%以内。
本工作首先应用工程方法对复合材料加筋板的压缩屈曲载荷和破坏载荷进行估算;然后开展复合材料加筋板的压缩屈曲实验,根据实验现象得到加筋板的屈曲及破坏形式,对实验中所记录的加筋板载荷-应变和载荷-位移曲线进行分析,得到压缩屈曲载荷以及破坏载荷等。
1 实验材料
实验件为带有4根工字型筋条的复合材料加筋板,如图1所示,两端部进行灌胶处理(灌胶段长为60 mm),作为其加载端。实验件尺寸为820 mm ×600 mm,壁板厚度a为3.25 mm,筋条间距b为150 mm。筋条的几何尺寸如图2所示。实验材料由中国航发北京航空材料研究院制造,采用碳纤维环氧树脂基单向带CCF300/5228A,厚度为0.125 mm,其力学性能参数如表1所示。加筋板中单向带的铺层顺序如表2所示。为了避免实验结果的偶然性,实验件共3件(记为C-1、C-2和C-3)。
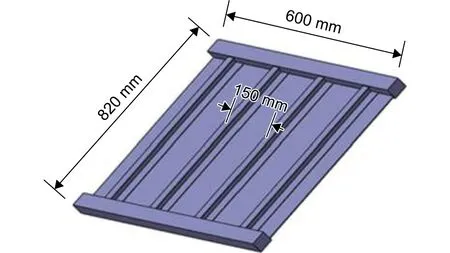
图1 复合材料加筋板Fig.1 Composite stiffened panel
2 复合材料加筋板压缩屈曲载荷及破坏载荷
2.1 复合材料加筋板压缩屈曲载荷估算
复合材料加筋板的主要屈曲形式有蒙皮局部屈曲、筋条局部屈曲和整体屈曲等[20]。在实际工程应用中,加筋板多为中等长度,若筋条先于蒙皮发生局部屈曲将会显著降低加筋板的承载能力,是不合理的设计,因此本工作主要研究的是筋条间蒙皮的局部屈曲。复合材料加筋壁板结构在承受屈曲载荷时,其屈曲形式主要为格间(指加强件之间的蒙皮段)屈曲失稳,加强件在屈曲失稳前几乎保持直线,起“屈曲分隔”的作用,因此通常将加筋壁板的格间局部屈曲失稳载荷作为压缩屈曲载荷[18]。
当沿层合板长度方向作用均匀平面力Nx时,四边简支矩形层合板受力情况如图3所示。
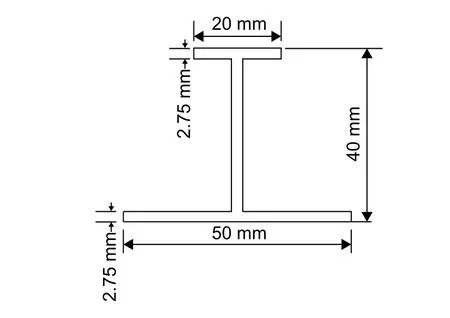
图2 筋条几何尺寸Fig.2 Geometric dimensions of stiffeners

表1 加筋板铺层顺序Table 1 Laying sequence of stiffened panels

表2 CCF300/5228A基本力学性能Table 2 Basic mechanical properties of CCF300/5228A
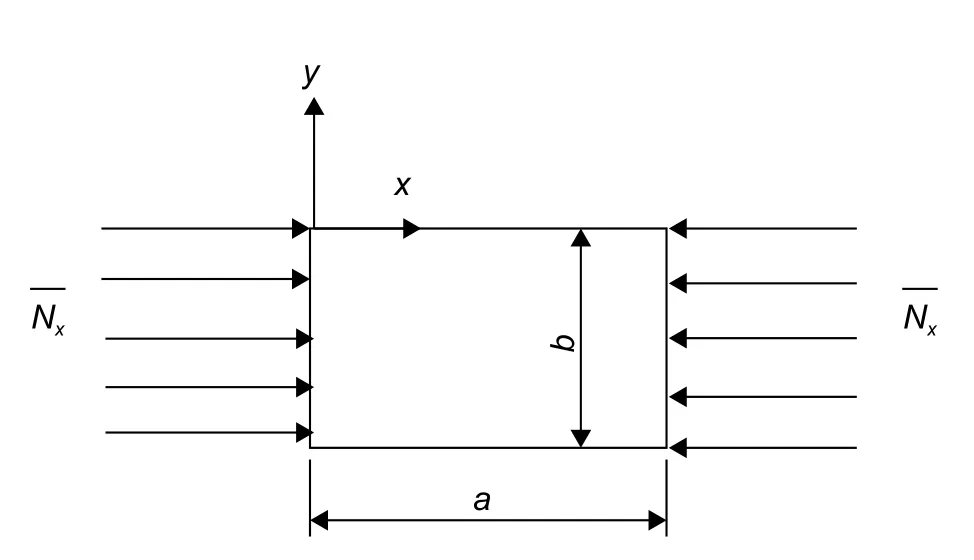
图3 均布单向平面压力下的简支层合板Fig.3 Simply supported laminated plates uniformly distributed under unidirectional plane pressure
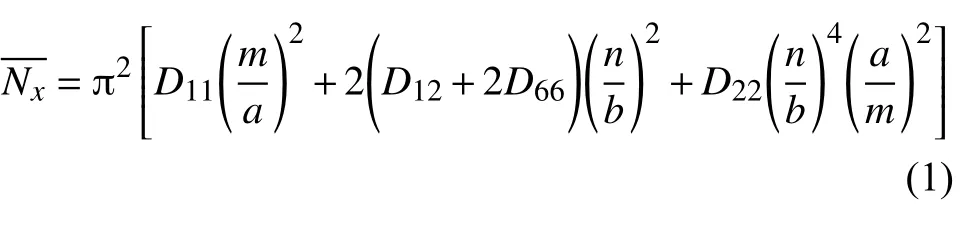
式中:m、n分别是x(长度方向)和y(宽度方向)屈曲的半波数;a、b分别是平板的长度和宽度,考虑实验夹具影响计算中取a=505 mm,b=105 mm;D11,D12,D13为弯曲与曲率之间的刚度系数,D66为扭转与扭转率之间的等效刚度系数。
显然当n=1时有最小值,所以临界屈曲载荷计算公式为:
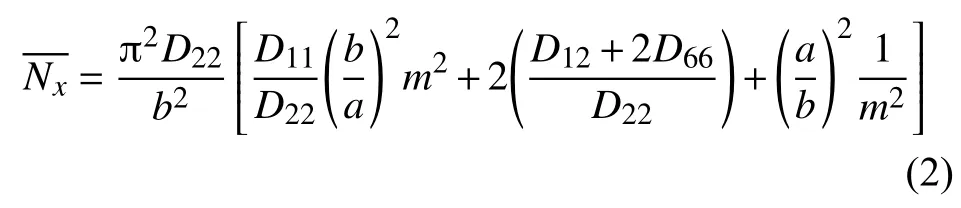
计算时,可取m=1,2,3……,计算得到其中最小的即为板单位长度上的压缩屈曲载荷。
根据单层铺层材料的力学性能、壁板几何尺寸计算得出壁板的等效弯曲刚度矩阵(N·mm)如式(3)所示:

计算得出m=1,2,3……8对应的(N/mm),如表3所示。
表3 半波数m 与(N/mm)关系Table 3 Relation between half wave number m and(N/mm)
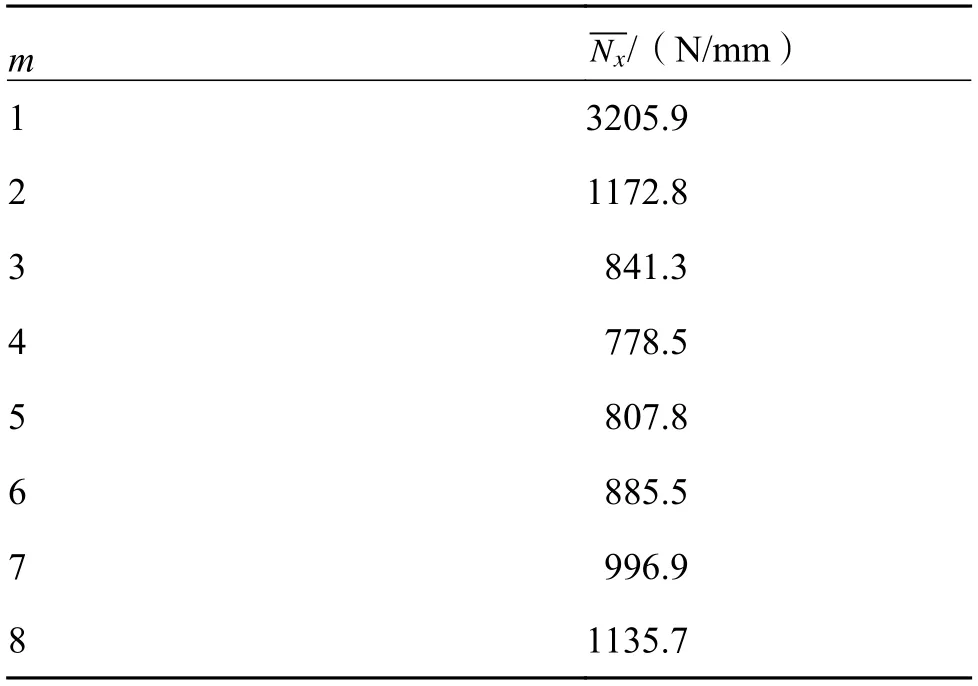
表3 半波数m 与(N/mm)关系Table 3 Relation between half wave number m and(N/mm)
从表3中可看出在m=4时,即长度方向半波数为4时,值最小,为778.5 N/mm。实验用加筋板宽度是600 mm,计算得到加筋板的压缩屈曲载荷为552.0 kN。
2.2 复合材料加筋板破坏载荷估算
复合材料加筋板后屈曲的分析和计算十分复杂,一般采用工程经验公式计算破坏载荷(也称为极限承载载荷),本节采用分段处理法[19]对加筋板的破坏载荷进行计算。定义加筋板的有效长细比为:

式中:L′为加筋板的有效柱长;ρ为加筋板的剖面回转半径。
按加筋板有效长细比将其失稳破坏形式分为3个区段,如图4所示。
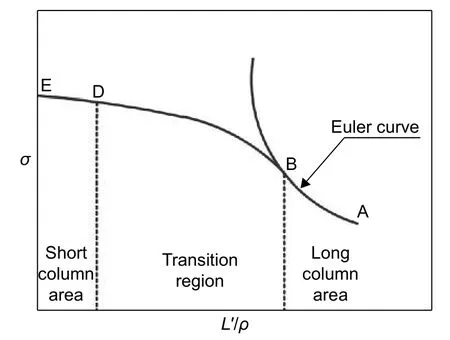
图4 加筋板三个区段失稳破坏曲线Fig.4 Failure curve of three sections of stiffened plate
在过渡区段(D-B)内,加筋板破坏之前,壁板或筋条先产生局部屈曲。实际使用中加筋板的失稳破坏形式多属于此种形式,因此可按此种失稳破坏形式进行估算。可应用式(5)估算加筋板的破坏应力:
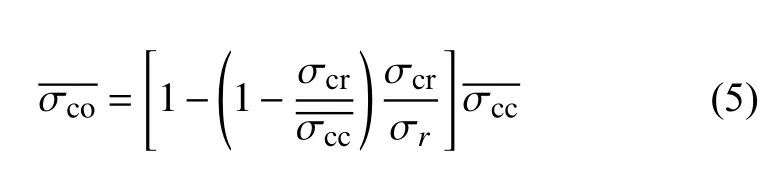
计算过程如下:
(1)壁板的平均局部屈曲应力 σcr。其中,,t为壁板厚度。2.1节计算的壁板压缩屈曲载荷为778.5 N/mm。
(2)加筋板的总体屈曲应力 σr按式(6)计算:
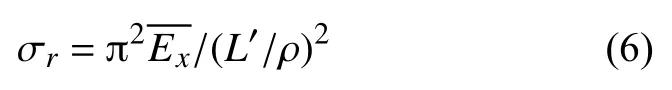

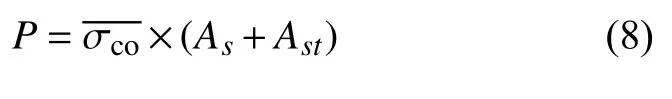
式中:As为平板截面积;Ast为筋条的截面积。
计算结果如表4所示。计算得到破坏载荷为878.6 kN。

表4 破坏载荷计算结果Table 4 Computational results of failure loads
计算实验用复合材料加筋板的压缩屈曲载荷和破坏载荷,分别为552.0 kN和878.6 kN。
3 实验方法与结果分析
3.1 实验方法
轴向压缩实验在WAW-3000B结构实验平台上进行,其加载控制系统采用MTS FLEX TEST40三通道控制器,其控制精度可达0.001 kN,最大加载量为3000 kN。针对实验件几何形式设计了实验夹具,主要包括上下平台,球形底座,上下凹槽,挡板,侧向加持板等。
测量载荷-应变曲线以及载荷-位移曲线使用DH-3816型静态应变测试系统测量载荷-应变曲线以及载荷-位移曲线,测量最大量程为 ± 19999 με,工作精度为最大量程的 ± 0.2%。在实验件上选取合适位置粘贴应变片和连接位移传感器,应变片的粘贴位置及编号如图5所示,位移传感器的连接位置如图6所示。
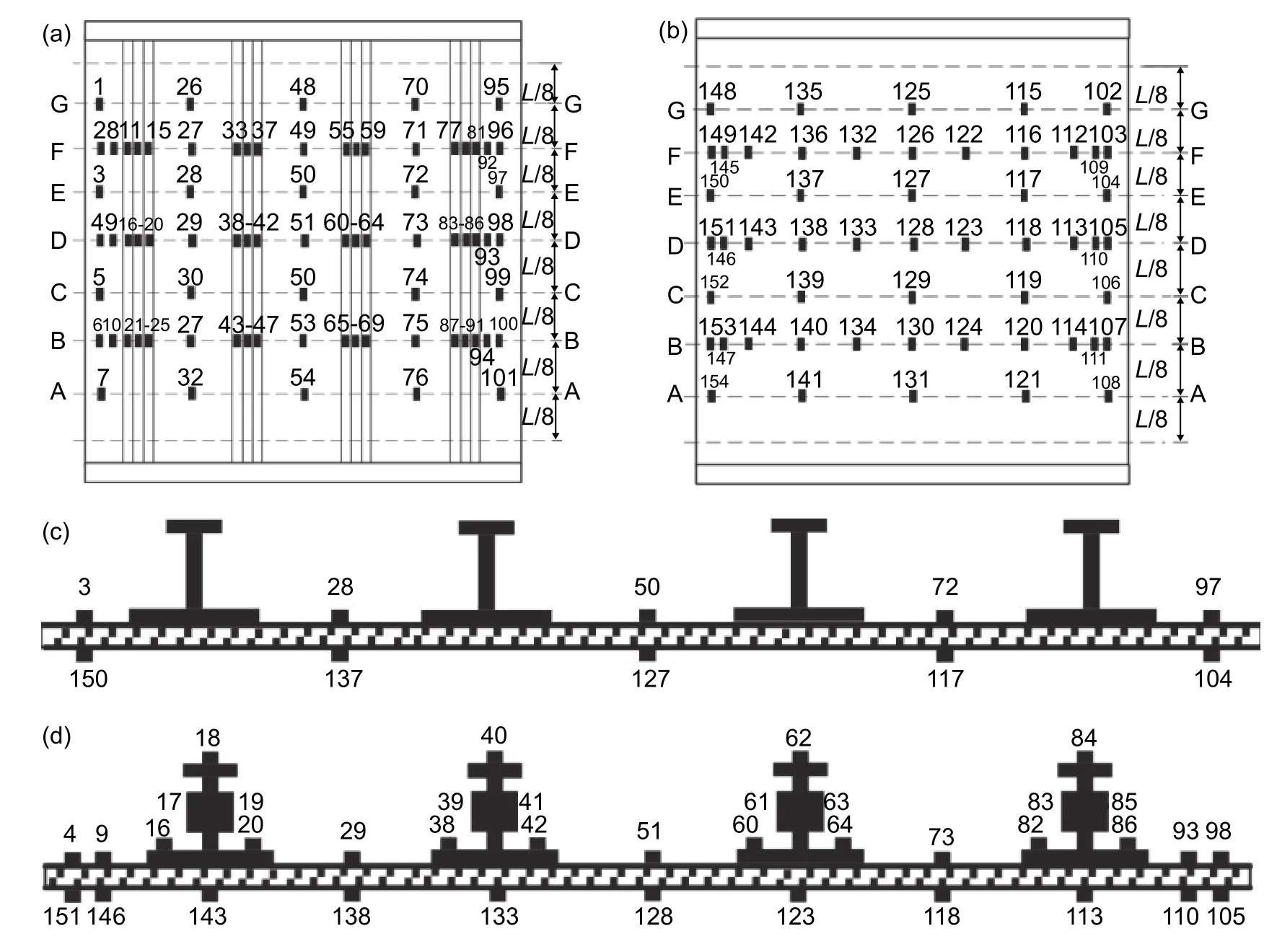
图5 压缩实验件应变片粘贴位置及编号(a)筋条面应变片粘贴位置及编号;(b)壁板面应变片粘贴位置及编号;(c)E-E截面示意图;(d)D-D截面示意图Fig.5 Position and number of strain gauge adhesion for compression tests(a)sticking position and number of stiffener strain gauges;(b)paste position and number of strain gauge on wall plate;(c)E-E section diagram;(d)D-D section diagram
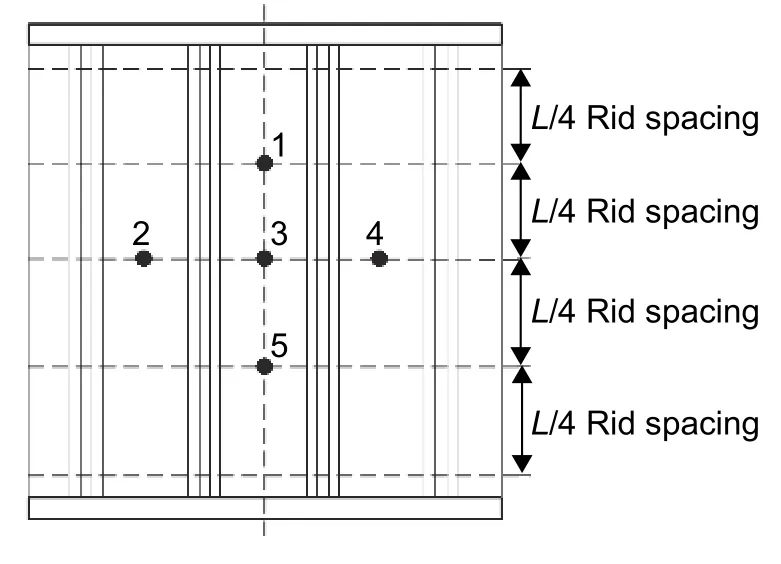
图6 位移传感器连接位置Fig.6 Connection position of displacement sensor

图7 C-1失稳形式Fig.7 C-1 instability form
进行轴压实验时,先按照50 kN为一级,加载2~3级,根据应变值对实验件的受力情况进行分析,通过对实验件及夹具安装位置的调整保证实验件受到均匀轴向的压缩载荷。具体要求是当实验件壁板面与筋条面对称位置上的应变值相差在± 10%以内,就认为满足压缩实验的加载要求。当调整好位置后,开始正式实验,加载分为预加载和正式加载两个阶段。预加载阶段以50 kN为加载梯度加载至300 kN后卸载,反复加载2次,若应变值及位移值具有较好的重复性,则开始进行正式加载。进行正式加载时,首先按照50 kN为一级进行加载,参考上文屈曲载荷估算值,加载到500 kN后以20 kN为一级加载至520 kN,保持载荷30 s,观察实验件是否坍塌破坏,若不破坏则加载至550 kN;之后按照每级载荷20 kN逐级继续加载直至实验件破坏。
3.2 实验结果与分析
本实验的3个实验件的实验现象类似,实验结果类似,具有重复性,故以第一件压缩实验件(C-1)为例,其实验现象如下:当加载载荷小于450 kN时,未发现实验件出现异常情况;当加载载荷为450 kN左右时,听到实验件发出间断的轻微响声;随着载荷的增加,在550 kN和600 kN之间时实验件陆续发出轻微的响声,当载荷达到580 kN左右时,可以通过壁板对光线的反射观察到实验件发生了屈曲失稳现象;加载至890 kN左右时,实验件发出较大的纤维断裂的响声,持续30 s后仍能继续承载;继续增加载荷,当加载至960 kN时,实验件突然发出巨大的响声,与此同时筋条与壁板出现大幅度的开裂,一侧夹持板被震脱开,实验件失去承载能力,发生坍塌破坏。实验过程中观察到的实验件失稳形式及破坏形式分别如图7和图8所示。从图中可以看出,C-1的屈曲失稳形式主要是壁板的局部屈曲失稳,破坏形式主要是筋条中部的断裂、脱粘和壁板中部的分层、鼓包和撕裂。
取C-1号实验件中间截面(D-D)壁板上的所有应变监测点的应变值做出载荷-应变曲线,如图9所示。取位移测量值做出载荷-位移曲线,如图10所示。由图9可以看出,在加载的初始阶段加筋板对称位置上的应变值相差较小,曲线整体呈线性增加趋势(压缩应变是负值),在此阶段中实验件在压缩载荷下发生均匀的压缩变形;当载荷增加到590 kN左右时载荷-应变曲线出现了明显的“分叉”现象,应变值的变化出现了明显的不一致的趋势。原因是当载荷达到压缩屈曲载荷时,加筋板的弯曲刚度发生了变化,实验件出现了壁板的局部屈曲失稳现象;屈曲失稳后加筋板并没有破坏,可以继续承载,说明复合材料加筋板存在后屈曲过程;但随着载荷不断地增加,加筋板的整体刚度不断下降,失稳现象愈加严重,当载荷达到970 kN时,实验件出现了筋条的断裂、脱粘现象,随之加筋板迅速破坏,失去承载能力。破坏载荷是压缩屈曲载荷的1.65倍。
由图9(a)可以看出,载荷达到590 kN左右后发生了屈曲失稳现象,128号位置的应变值由负逐渐变为正,并有逐渐变大的趋势,说明128号位置的壁板在达到屈曲失稳之后,不再产生压缩变形,并逐渐转为拉伸变形,同时,与128号壁板位置相对应的51号壁板,在达到屈曲失稳后继续产生压缩变形,而且变形速率明显高于屈曲失稳之前,由此可判断128,51号位置的壁板产生了弯曲波,根据两个位置的应变趋势,可得出弯曲方向为向壁板面弯曲;由图9(b),(c)可以看出29,73号位置的壁板由压缩变形转为拉伸变形,138,118号位置壁板的压缩变形不断增大,表明在该位置也发生了屈曲,但屈曲方向与51,128号位置的壁板方向相反,即向着筋条方向发生弯曲;图9(d)有较大的不同,在发生了屈曲失稳之后,9,146,93,110号四个位置(壁板两端)呈现出较为一致线性变化趋势,表明在这些位置壁板没有发生较为明显的弯曲,因为在实验件的两端安装了加持板,以防止实验件发生弯曲变形。同理,将C-2和C-3号实验件中间截面(D-D)壁板上的所有应变监测点的应变值做出载荷-应变曲线,取位移测量值做出载荷-位移曲线,发现该实验件的压缩屈曲形式和壁板的弯曲方向与C-1号相同。

图8 C-1破坏形式(a)筋条的断裂、脱粘;(b)壁板分层、鼓包和撕裂Fig.8 C-1 failure form(a)fracture and debonding of stiffeners;(b)wallboard stratification,bulging and tearing
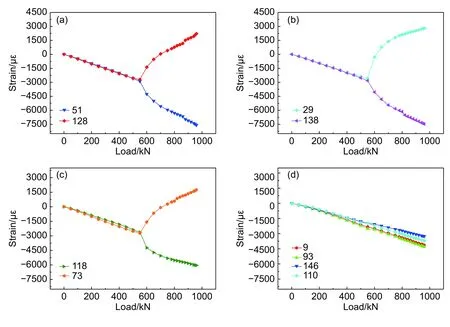
图9 C-1中间截面壁板应变监测点的载荷-应变曲线Fig.9 Load-strain curve of strain monitoring point of wall panel with intermediate section in C-1(a)load-strain curve of 73and 118 test points;(b)load-strain curve of 9,93,110 and 146 test points
由图10(a)和图10(b)可以看出,在加载初期,位移测量点的位移基本保持不变,说明加筋板水平方向上位移很小,此阶段中加筋板只出现轴向的压缩变形;当载荷增加到580 kN左右时,位移-载荷曲线出现了明显的“分叉”现象,一部分有陡升的趋势,一部分则有陡降的趋势,此时加筋板有了水平方向上的位移,说明此时加筋板出现了失稳现象;当载荷进一步增加,实验件并没有破坏,进入后屈曲阶段;当载荷增加到970 kN时,加筋板由于失稳过于严重,筋条出现断裂、脱粘,加筋板迅速破坏。
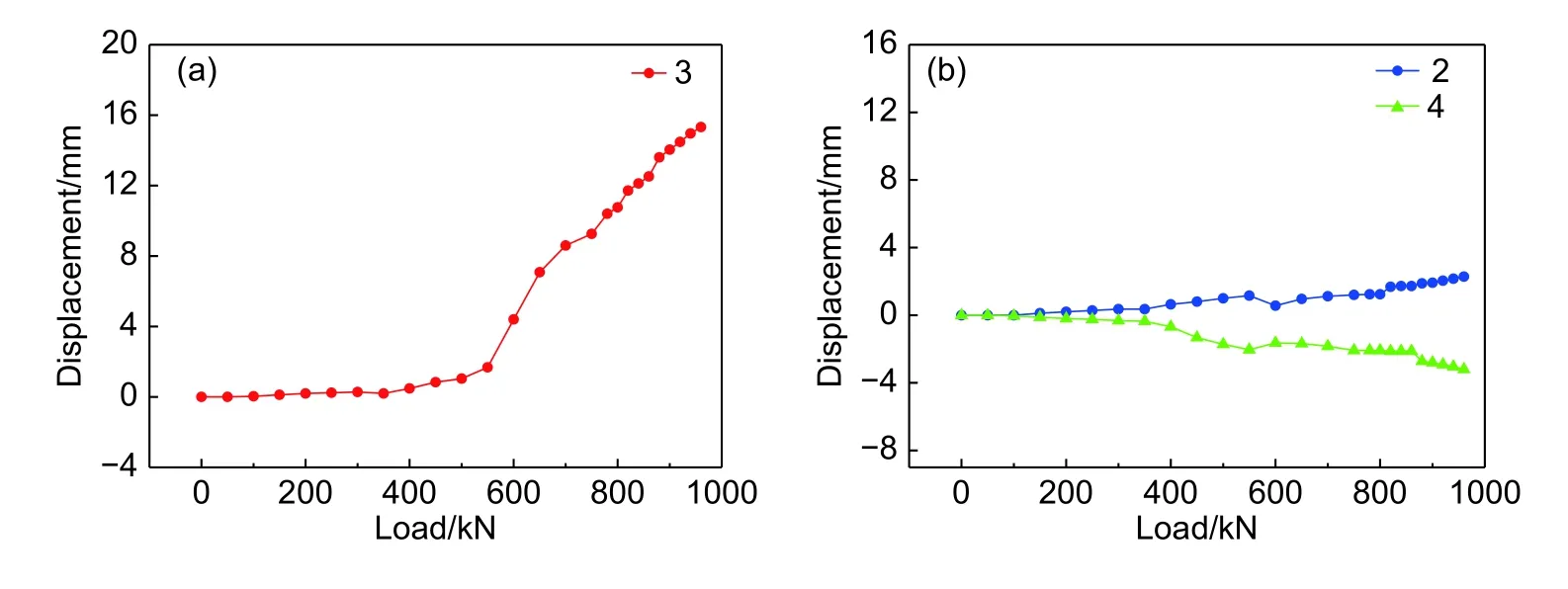
图10 C-1位移测量点的载荷-位移曲线Fig.10 Load-displacement curve of C-1 displacement measurement point(a)load-displacement curve of 3 displacement measurement point;(b)load-displacement curve of 2 and 4 displacement measurement point
对实验过程中整个加筋板在载荷作用下的压缩量进行记录,得到了加筋板的载荷-压缩量曲线如图11所示,该曲线呈现良好的线性,而且有一个明显的“拐点”,如图中所标注,在该“拐点”之后曲线表现出斜率的减小,而斜率的变化也表明了加筋板由于发生屈曲失稳而引起的刚度下降,在该点的载荷为580 kN左右,与前文估算结果一致,验证了估算结果的准确性。
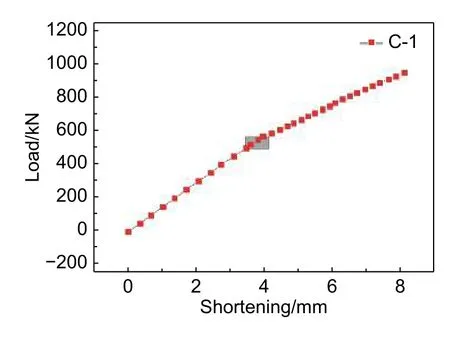
图11 C-1实验件载荷-压缩量曲线Fig.11 Load-shortening curve of C-1 test piece
将压缩实验结果汇总于表5,从表中可看出三件实验件的实验结果分散性较小,说明实验效果较好。表中,N1=平均破坏载荷/平均压缩屈曲载荷。从表中可以看出三件实验件的平均破坏载荷是平均压缩屈曲载荷的1.65倍,说明加筋板具有较强的后屈曲承载能力,工程中可充分应用加筋板的后屈曲承载能力提高结构的利用效率。

表5 压缩实验结果Table 5 Compression experiment results
4 结论
(1)应用工程方法计算了复合材料加筋板的压缩屈曲载荷以及破坏载荷,与实验结果的误差分别为6.12%和9.31%,具有较高的计算精度。
(2)C-1、C-2和C-3的压缩屈曲载荷和破坏载荷接近,三件实验件的实验结果分散性较小;平均压缩屈曲载荷和破坏载荷分别为588.0 kN和968.87 kN,后者是前者的1.65倍,说明加筋板结构在压缩载荷下存在后屈曲过程,且具有较强的后屈曲承载能力,应在工程中加以充分利用。
(3)根据载荷-应变曲线及载荷-位移曲线可以得出:载荷达到590 kN左右后发生了屈曲失稳现象,并且失稳壁板不同位置的弯曲方向也不相同。
(4)复合材料加筋板在压缩载荷下的破坏位置一般在加筋板的中部,破坏形式主要是筋条的断裂、脱胶,壁板的分层、鼓包及撕裂。

