基于Canny算子的滤棒数量检测方法
曹维林,李 捷,孙顺凯,陆海华,陈海涛,陈 明,陈思萧,沈苗杰
浙江中烟工业有限责任公司宁波卷烟厂,浙江省宁波市奉化经济开发区葭浦西路2001号 315504
随着烟草行业“降本增效”要求的提出,卷烟生产过程中的材料消耗越来越受到关注,滤棒消耗也是其重要组成部分。考察滤棒消耗的前提条件是精确统计每托盘滤棒数量,但目前烟草行业尚未建立起有效检测滤棒数量的方法,卷烟企业大多采用称重法、人工计数法、经验法等方法进行统计,存在统计速度慢、效率低、误差大等问题。针对此问题,李哲[1]提出在发射机端的每个发射管道内配置一个伺服控制器,用于控制滤棒发射时间并对发射的滤棒数量进行计数,但由于伺服控制器安装在发射管道内,如果滤棒在进入发射管道前,设备出现故障导致滤棒损坏而产生的滤棒消耗则无法统计,因此存在一定误差。当前数字图像处理[2]、机器视觉[3]等技术在物体数量检测方面已有较多研究报道。1972年,Duda等[4]首次提出了基于霍夫变换(Circle Hough Transform,CHT)的圆检测算法,该算法结构简单,抗噪能力强,但计算量和存储量大,在工业检测时效性要求下,存在速度慢、效率低等缺陷。边缘是图像基本特征之一,边缘检测在图像处理、机器视觉、目标检测与识别、图像分割等领域应用广泛[5-8]。其中,Canny算子[6-7,9-10]、Log 算子[11]、Sobel算子[12]等都是对图像边缘进行检测的微分算子方法,通过微分检测图像中边缘灰度值的变化进而检测出边缘信息。Canny算子检测出的边缘较细,定位较准确,但容易受梯度幅值和双阈值的影响,且不具有自适应性;Log算子首先对图像进行平滑滤波去噪,但滤除噪声效果越好,图像损失的细节越多,同时也会滤除边缘信息,因此在边缘信息精度与滤除噪声之间存在矛盾;Sobel算子通过计算像素四邻域梯度值来检测边缘信息,可以较好地检测低噪声图像,但对于混合复杂、多噪声图像处理效果不佳。OpenCV(Open Source Computer Vision Library)[7,10,13]是 Intel公司开发的由 C 函数和部分C++库构成的开源计算机视觉库,平台功能强大且支持Canny算子,具有代码开源、图像及计算机视觉处理函数丰富、执行效率高、跨平台性好等优点,广泛应用于图像特征检测、物体运动跟踪与识别、医学成像等领域。为此,基于Canny算子建立了一种滤棒数量检测方法,以期提高滤棒数量统计精确性,为降低卷烟生产消耗提供数据支持。
1 材料与方法
1.1 材料
长支烟、中支烟和短支烟滤棒样品,圆周分别为(24.50±0.20)mm、(24.20±0.20)mm 和(22.00±0.20)mm(均由浙江中烟工业有限责任公司宁波卷烟厂提供),各随机抽取20托盘共60托盘进行编号。
1.2 设备和仪器
CCD 相 机(acA4112-8gm-Basler ace,德 国Basler集团);镜头(Lens Kowa LM12HC F1.4 f12.5mm 1",日本兴和集团);光源(条形白光);笔记本电脑(ThinkPad T480,联想集团),硬件环境为:Windows10(64)+Intel(R)Core(TM)i5-8250U CPU@1.60GHz 1.80GHz+8GB RAM。
1.3 检测方法
首先利用Canny算子对托盘滤棒进行边缘检测,再利用图像形态学中的膨胀运算对边缘进行处理[14],从而精确定位滤棒位置。Canny算子检测图像边缘时分为4步:①使用高斯滤波函数对图像进行滤波去噪;②对去噪后图像计算梯度幅值;③在梯度幅值方向上进行非极大值抑制;④通过双阈值处理实现边缘点检测及连接[10,15]。
1.3.1 高斯滤波
Canny算子使用的是高斯滤波器,其在图像处理中去噪性能优越,通过滤波模板与原图进行卷积,对图像进行平滑处理,二维高斯函数为:

式中:σ是人为设置的一个重要参数,决定了图像的平滑程度。σ值过大会使图像过于平滑,丢失有用的边缘信息;σ值过小会降低对噪声的抑制效果,出现虚假边缘信息。
由式(1)可得到其梯度矢量公式:

为提高运算速度,对式(2)中的滤波卷积模板进行分解,分别得到x和y方向的一维滤波器:

1.3.2 梯度幅值和方向
利用计算机进行数字图像处理时,通常通过2×2窗口的一阶偏导数有限差分进行计算,那么图像I(i,j)在x和y方向的偏导数分别为:

1.3.3 非极大值抑制
为得到更精细的图像边缘信息,需要对图像进行梯度方向的非极大值抑制。具体过程为:遍历图像,计算出每一个像素点的梯度幅值和方向,若某个像素点的幅值小于该像素点梯度方向上其他任意两个像素幅值中的任意一个,那么该像素点判定为非边缘点,同时将该点的幅值设置为0;否则该像素点可能为边缘点。
1.3.4 双阈值检测和边缘连接
如果将非极大值抑制图像中梯度值不为0的像素点连接成边缘,那么这些边缘中肯定会包含大量虚假边缘。因此,在Canny算子中需要对非极大值抑制后的图像进行双阈值处理,以消除虚假边缘以及间断边缘。具体过程为:分别设置高低两个阈值,对非极大值抑制图像的边缘灰度值进行统计分析,灰度值大于高阈值的像素点全部提取,直接作为选定的边缘像素点,此时虚假边缘较少,但间断点会较多;将灰度值小于低阈值的像素点作为非边缘像素点,此时图像边缘信息较全面,但也会包含虚假边缘。为此,通过高低阈值分别处理两幅图像。利用高阈值将选定的边缘像素点连接成线,利用低阈值将灰度值处于低阈值与高阈值之间的像素点提取出来;当遇到间断点时,如果提取的像素点与选定的边缘像素点是相连接的,则认为这些像素点也是边缘。如此往复,直至得到连续的边缘。
1.4 检测过程
基于图像处理技术,利用Python3版本的计算机编程语言、OpenCV及其丰富的函数库,通过采用Canny算子对托盘滤棒进行边缘检测,并最终检测出滤棒数量。检测流程见图1。

图1 滤棒数量检测方法流程图Fig.1 Flow chart of counting method for filter rods
Step1:读取图片Img。使用高清相机拍摄滤棒图像,利用函数cv2.imread()读取图片。
Step2:Img转灰度图Gray。利用函数cv2.cvtColor()实现图像Img的灰度化,见图2。

图2 滤棒灰度图Fig.2 Grayscale images of filter rods
Step3:Gray转二值图Binary。Gray中像素点灰度值高于127的置为255,否则置为0。利用函数cv2.threshold()实现图像二值化,见图3。Step4:通过Canny算子对Gray进行边缘检测。利用函数cv2.Canny()得到滤棒边缘图Edges,见图4。

图3 滤棒二值图Fig.3 Binary images of filter rods

图4 滤棒边缘图Fig.4 Edge images of filter rods
Step5:利用Edges进行膨胀运算得到图像Dilate。由于一个托盘中滤棒数量较多,排列紧密且颜色差异不大,利用Canny算子虽然可以检测出滤棒的大致边缘,但仍会存在间断点和虚伪边缘,因此需要对这些边缘进行处理。膨胀是图像形态学基本运算之一,通过对图像中白色部分(高亮部分)进行膨胀,可以扩大图像的高亮区域。利用函数cv2.dilate()进行膨胀运算,见图5。

图5 边缘膨胀图Fig.5 Images of dilated edges
Step6:利用Binary减去Dilate得到滤棒位置Result_Canny。图5中的高亮(白色)部分为边缘膨胀后的结果,虽已经看不出滤棒边缘形状,但消除了间断点和虚伪边缘,此时在二值图Binary中,去除膨胀后边缘即可得到滤棒大致位置。利用函数cv2.subtract()得到滤棒位置图,见图6。

图6 滤棒位置图Fig.6 Images of filter rod positions
Step7:利用Result_Canny进行膨胀得到滤棒形状Result_Canny_Dilate。对图6再次进行膨胀运算,即可恢复滤棒原始形状。为了提高滤棒数量检测精度,膨胀后的高亮部分不可粘连在一起,见图7。
Step8:检测Result_Canny_Dilate中每支滤棒的圆心和半径。圆心数量Count即为滤棒数量,利用函数cv2.findContours()实现圆心和半径检测。

图7 滤棒图Fig.7 Images of filter rods
Step9:通过检测出的圆心和半径在Img中画圆得到检测结果Result_Img。利用函数cv2.circle()得到检测结果,见图8。

图8 滤棒检测结果图Fig.8 Image of detection result of filter rods
2 结果与分析
由表1可见,长支烟、中支烟和短支烟滤棒各20托盘,长支烟滤棒误检率0.14%,漏检率0.99%,准确率99.01%;中支烟滤棒误检率0.08%,漏检率0.66%,准确率99.34%;短支烟滤棒误检率0.08%,漏检率0.67%,准确率99.33%。系统平均准确率达到99.27%,平均耗时3.97 s/托盘,表明该检测方法具有较高的准确性和通用性。根据表1数据计算可得,长支烟、中支烟、短支烟滤棒检测准确率标准偏差分别为0.28、0.36、0.42,离散程度较低,表明该方法具有较好的鲁棒性。此外,相同数据采用经验法进行统计,长支烟、中支烟、短支烟滤棒检测准确率分别为98.63%、98.69%和97.67%,平均为98.33%。可见,采用本方法检测准确率可提高0.94百分点。

表1 滤棒数量检测数据Tab.1 Detection data of filter rod number
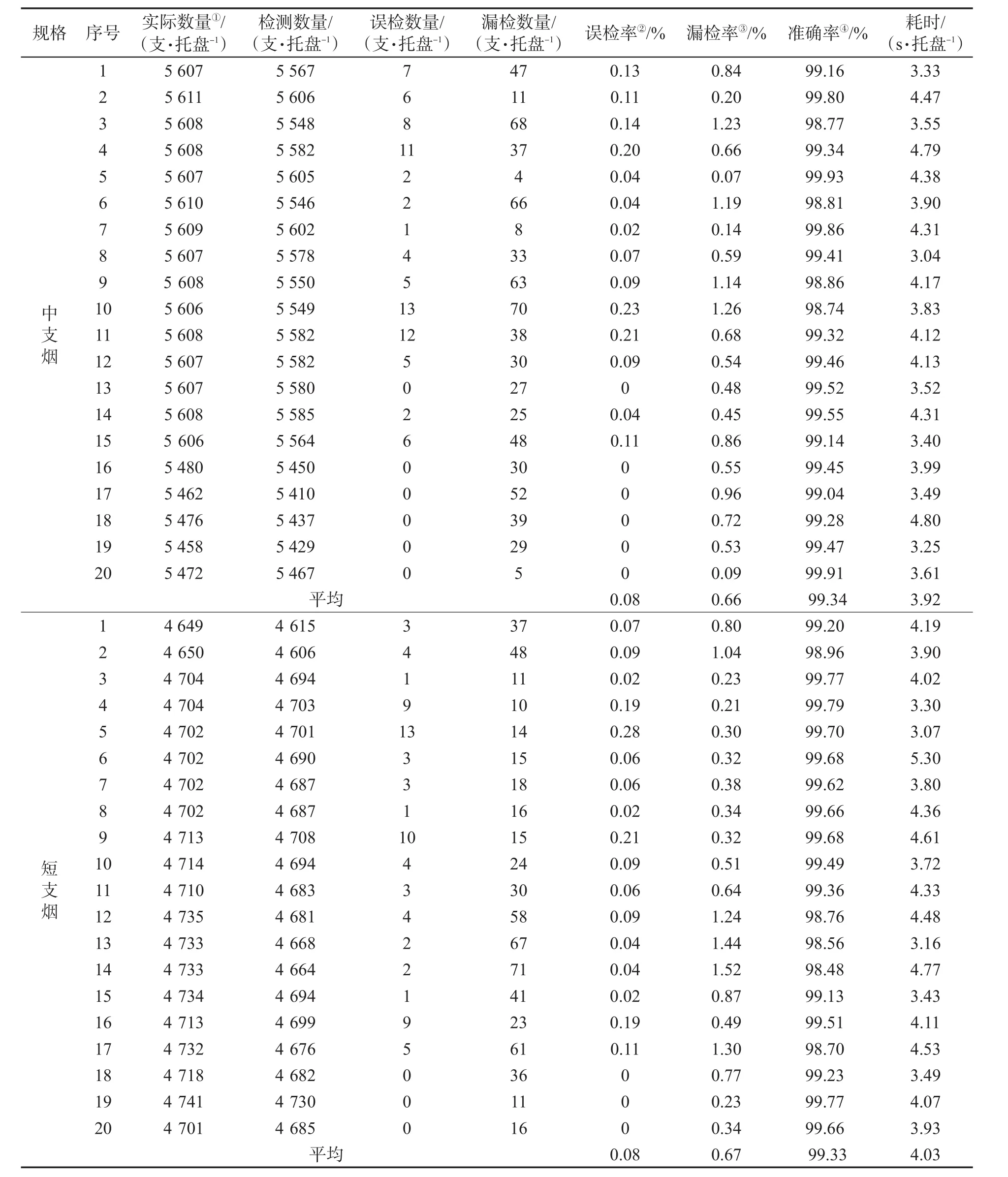
表1(续)
3 结论
基于Canny算子对整托盘滤棒进行边缘检测,再利用膨胀运算和滤棒的圆形特性,精确定位滤棒位置,从而检测出滤棒数量。以长支烟、中支烟和短支烟滤棒样品为对象进行测试,结果表明:该检测方法能够实现滤棒数量的精确统计,准确率达到99.27%,且不会因滤棒圆周变化而无法检测其边缘,适用于各种圆周滤棒,具有较好的通用性和鲁棒性。在实际生产中若能使用更高配置的计算机,将会进一步降低检测耗时,提高检测效率。

