天然气水合物降压开采过程中储层应力规律分析

金 颢, 张俊斌, 何玉发

天然气水合物降压开采过程中储层应力规律分析

金 颢, 张俊斌, 何玉发

(中海石油(中国)有限公司深圳分公司深水工程技术中心, 广东 深圳 518000)

为了研究天然气水合物降压开采过程的储层应力及其稳定性, 运用线性多孔弹性力学和岩石力学知识, 考虑水合物储层原始应力、孔隙压力、渗流附加应力及降压开采水合物过程中水合物饱和度的变化, 建立了降压开采天然气水合物储层的力学模型, 结合墨西哥湾某处水合物藏的基本参数, 对降压开采水合物储层应力变化和开采过程的储层稳定性进行研究。结果表明: 井底压力是影响水合物储层应力变化的关键因素之一; 渗流附加应力在一定程度上减小了储层的应力; 水合物分解储层应力发生变化, 储层应力在井壁处的波动最大, 井壁处是整个储层所受轴向偏应力最大的位置, 因此井壁处是优先发生剪切破坏的位置; 为了储层的稳定性, 降压开采水合物生产压差应小于2.19 MPa。

降压开采; 天然气水合物; 渗流附加应力; 水合物饱和度; 临界生产压差; 储层稳定性

目前, 天然气被认为是21世纪的一种未来优质、高效、洁净的能源, 天然气的蕴藏量为现有地球化石燃料总碳量的2倍左右[1]。然而, 天然气能否真正成为未来的可用能源, 关键在于能否有效地对天然气水合物进行合理的开采[2]。

天然气水合物广泛分布于海底沉积层和极地冻土带。通常天然气水合物以固态形式充填于多孔介质储层中, 天然气水合物成藏相比于常规储层条件要复杂, 并且不具备流动性。因此, 根据天然气水合物的存在条件和基本性质决定了天然气水合物的开采方式[3]。天然气水合物理论上的开采思路是: 首先通过一定的方式打破天然气水合物储层的平衡性, 促使水合物在储层中发生分解, 进而开采出分解的天然气。目前, 天然气水合物广泛的开采方法有: 注化学剂法、加热法和降压法等三种[4]。注化学剂法较加热法作用缓慢, 且二者使用的费用昂贵; 降压法是通过降低储层压力使其低于水合物相平衡压力引起储层中水合物分解的方法, 降压法开采天然气水合物由于其不需要昂贵的连续激发, 所以被认为是最具有商业前景的开采方法[5]。

天然气水合物在降压开采过程中, 由于降低井底压力, 打破了水合物储层的稳定性, 促使水合物发生分解。受水合物分解的影响, 分解区水合物储层胶结性变差、力学强度大幅度降低, 进而近井区储层呈现出弱胶结、低强度、高孔渗的特点, 类似于常规疏松砂岩[6]。由于水合物降压分解引起水合物储层物性参数及岩石力学性质等发生一系列变化, 如水合物饱和度减小、储层内聚力降低、储层孔隙度增大、渗透率增大等, 导致水合物储层应力发生改变, 致使水合物储层稳定性降低, 达到或超过本身固有的剪切强度, 使近井区水合物储层发生剪切破坏, 从而影响天然气水合物安全有效的开采。

由于天然生成的天然气水合物岩样取芯困难, 目前, 国内外学者对天然气水合物的研究大多是在实验室内完成的。因此, 基于前人的研究, 通过分析水合物储层的稳定性, 本文在采用降压法开采天然气水合物过程中考虑储层渗流附加应力的影响, 同时利用叠加原理建立了天然气水合物降压开采过程中储层稳定性的力学模型, 进行了降压开采水合物过程中储层应力的模拟计算, 分析天然气水合物在降压开采过程中储层应力变化特征及储层的稳定性, 为有效开采天然气水合物提供一定的理论基础。

1 水合物储层模型建立

通常天然气水合物存在于疏松砂岩沉积层中, 埋藏深度浅。在降压开采天然气水合物过程中, 可将整个水合物储层划分为两个区域, 即水合物分解区、储层稳定区, 如图1所示[4, 7]。降压开采天然气水合物时, 当水合物储层内压力低于水合物相平衡时, 打破了水合物储层的平衡条件, 促使水合物发生分解。天然气水合物的分解将会导致储层的稳定性发生改变, 而水合物储层的应力在一定程度上影响储层的稳定性。因此, 水合物储层应力的变化成为影响水合物储层稳定性的重要因素, 而井底压力是分析水合物储层应力变化的关键因素。

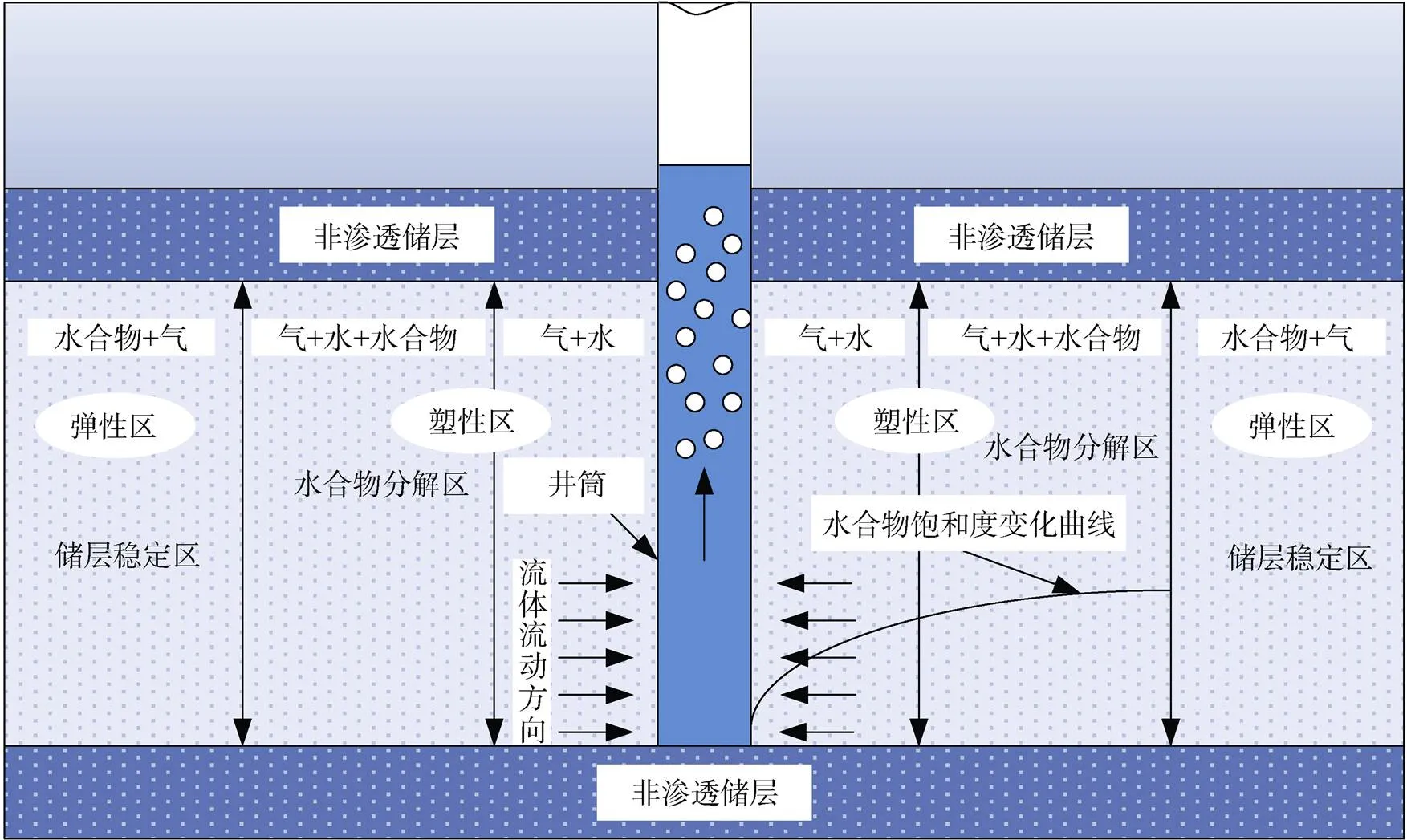
图1 水合物储层区域划分示意图

在研究降压开采天然气水合物储层应力变化时, 结合国内外学者建立的有关水合物饱和度、储层孔隙度、内聚力及储层应力等相关模型之间的关系, 构建水合物储层力学模型。由于降压开采天然气水合物的过程是非等温渗流过程, 因此该模型在研究过程中做了如下简化假设: (1) 天然气水合物储层为均质、各向同性的线弹性体。(2) 水合物储层仅考虑三相三组分。三相: 气、水、水合物; 三组分: 气、水、水合物。其中, 水合物为固相, 气体仅含甲烷, 且不重新生成新的水合物。(3) 降压开采水合物过程中, 水合物储层的温度变化忽略不计, 本文注重考虑井底压力的变化影响水合物储层应力改变的问题。(4) 仅考虑气、水两相流, 且两相渗流符合广义Darcy定律。(5) 井为垂直井。

1.1 水合物储层稳定性模型建立

在降压开采水合物前, 水合物储层受上覆岩层压力、最大水平主应力和最小水平主应力, 水合物储层处于应力平衡状态。当水合物储层被钻开时, 近井区水合物储层应力平衡被打破, 储层应力发生变化, 引起水合物储层应力的重新分布, 水合物储层的稳定性发生改变。因此, 井周围的应力分布可表示为[8-9]:

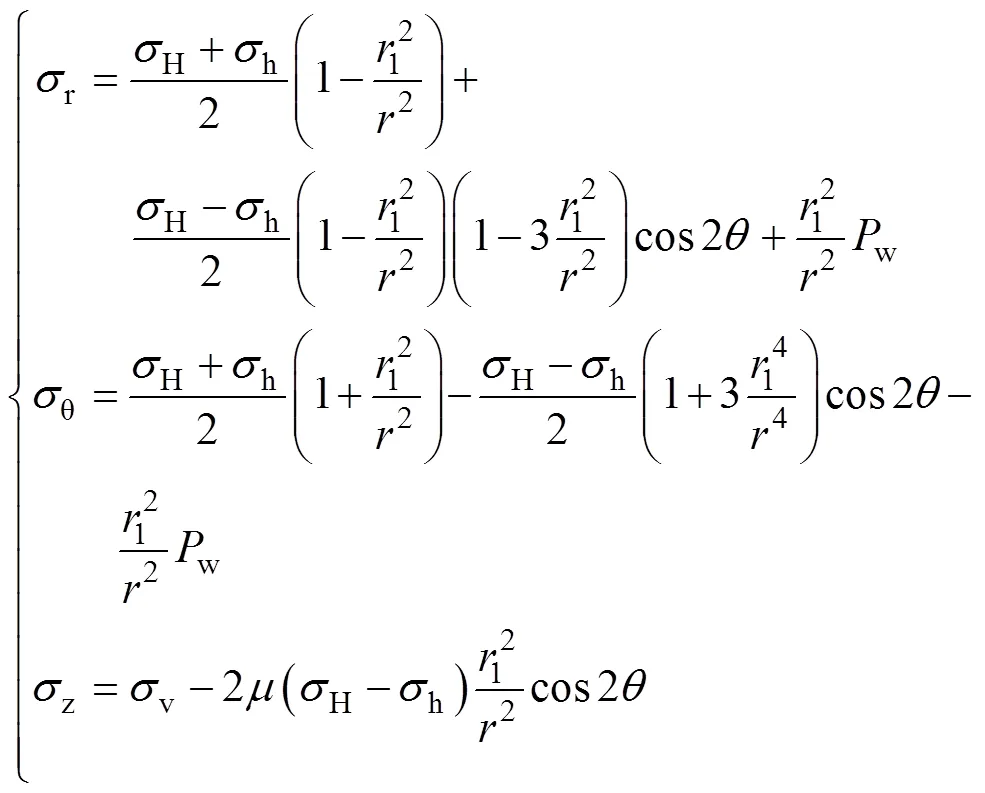
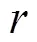
刘玉石等[10]通过运用有限元方法分析了井周储层稳态达西渗流时储层井壁围岩应力的变化, 从而得出井壁处的径向应力和周向应力与线弹性理论计算的结果存在很大的差别。水合物储层为多孔介质储层, 考虑到水合物储层的渗透性, 同时又由于储层流体在向孔隙中的径向流动过程中会对储层周围产生应力, 因此渗流附加应力会对储层产生一定的影响, 其相关表达式为[11]:

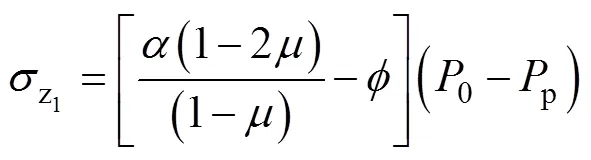
应用线性叠加原理, 由公式(1)和(2)得到天然气水合物储层近井区任意一点(≥1)处的应力分布式如下:

(1) 初始条件

天然气水合物开采前储层压力满足:

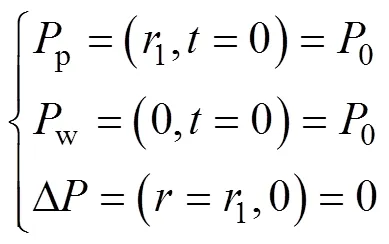
(2) 近井区水合物储层初始分量

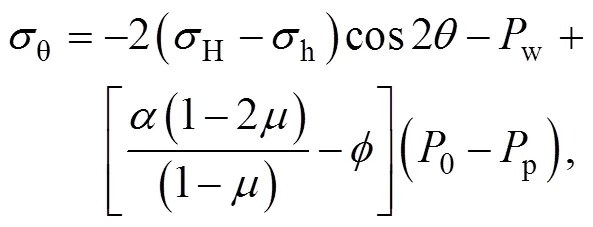
1.2 水合物储层物性参数

(1) 水合物储层孔隙压力的分布

开采前, 整个水合物储层处于稳定的状态, 储层中各点压力均等于原始地层应力。假设天然气水合物储层为一圆形区域, 在降压开采水合物过程中, 圆形封闭储层中任意一点时刻的压力满足弹性不稳定渗流边界条件, 其控制方程可表示为[12-13]:

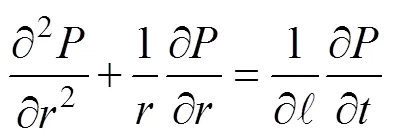
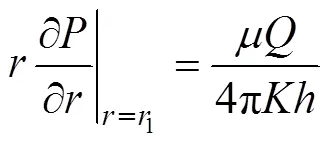
整理方程(8), 得到降压过程中水合物储层孔隙压力的分布函数:

当=1时, 得到井底压力w随时间变化的关系式为:

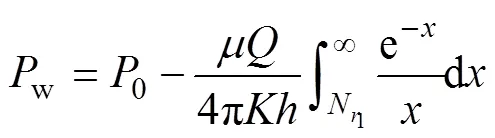
式中:为水合物储层厚度, m;为通过井孔的砂岩流量, cm3/s。

通过式(9)及式(10)可得:

式(11)可化为:

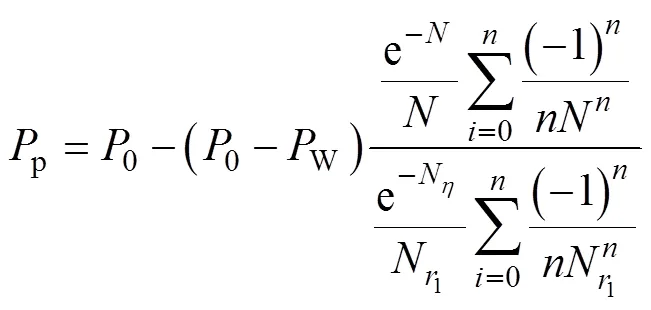
(2) 水合物饱和度随时间变化

降压开采水合物过程中水合物分解动力学方程可表示为:

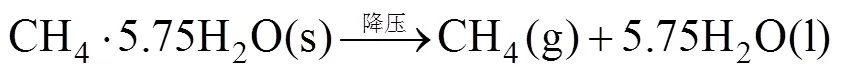
根据降压法开采中Kim-Bishnoi模型, 天然气水合物分解速率可表示为:

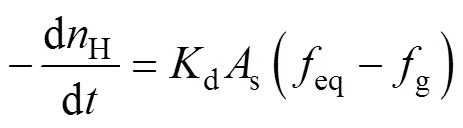
水兴百业旺。结合饮水安全工程建设，各地的乡村振兴建设也搞得有声有色。有了水，农户就把改厕、改灶、改路结合起来，很多农村的面貌焕然一新。

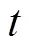
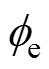
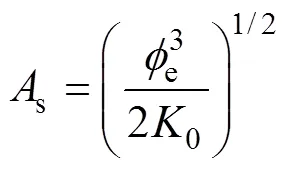
分解区水合物储层内气、水、水合物之间的关系式:

H+W+g= 1, (16)

其中,H=HH/H, 式中:H为分解水合物的体积;H为水合物物质的量, mol;H为水合物密度, 0.918 g/cm3。

多孔介质孔隙体积为:

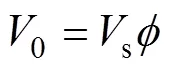
其中,s= 2πd。

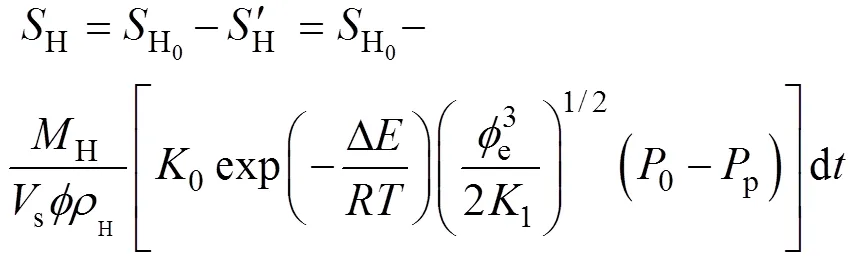
(3) 水合物储层孔隙度

随着水合物储层埋深、状态分布等特点, 水合物储层物性参数发生变化。随着埋深的增加, 地层沉积压实作用增大, 水合物储层孔隙度减小。多孔介质储层孔隙度与有效应力关系式为[15-16]:

Nazridoust等[17]假设天然气水合物储层孔隙度均匀分布且忽略了温度的影响, 得出储层孔隙度与水合物饱和度之间的关系式为:

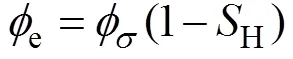
由式(20)和式(21), 可得到孔隙度变化动态模型:

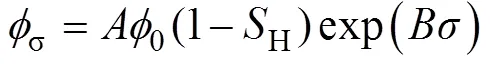
式中:为储层有效应力, MPa。

(4) 水合物储层内聚力及有效应力

在降压开采水合物过程中, 由于水合物的分解导致储层胶结性变差, 储层内聚力减小。随着水合物的分解, 水合物储层的内聚力降低, 储层内聚力与孔隙度之间的数学表达式如下[18]:

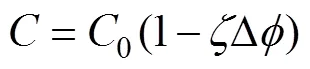
式中:为水合物分解后储层内聚力, MPa;0为初始水合物储层内聚力, MPa;为假设为1.2;为水合物储层孔隙度增量。

应用Terzaghi有效应力原理, 设储层岩石应力受压为负, 受拉为正[19], 其表达式为:

式中:为有效应力, MPa;v为储层原始垂向应力, MPa;为Biot系数;为Biot有效应力参数。

(5) 天然气水合物相平衡

天然气水合物广泛分布于极地冻土带和海底沉积层中, 水合物在储层中存在稳定带即水合物在储层中特定温度和压力条件下的一个范围, 在这个范围内水合物达到相平衡, 甲烷水合物相温度和压力平衡采用Makogon[20]模型计算, 得出表达式为:

lge=(–0) +(–0)2+, (25)

式中:e、0为分别是水合物分解的平衡压力(MPa)和平衡温度(K);= 0.034 2K–1,= 0.000 5K–2,= 6.480 4。

由于降压开采水合物导致的变形几乎是注热的10倍[21], 因此本文在研究降压开采水合物过程中, 假设水合物储层内的温度变化忽略不计。

(6) 储层稳定性判据准则

在研究水合物储层的稳定性时, 运用Drucker- Prager准则进行判断:

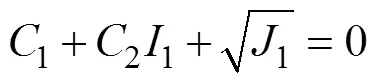
即,

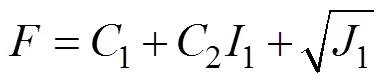
降压开采水合物过程中生产压差的计算公式表示为:

Δ=0–w, (28)

式中: Δ为水合物储层临界生产压差, MPa;0为原始水合物储层的孔隙压力, MPa;w为井底压力, MPa。

将式(3)、(29)代入(28)化简, 最终得到降压开采水合物过程中储层稳定性指数与生产压差之间的关系式为:

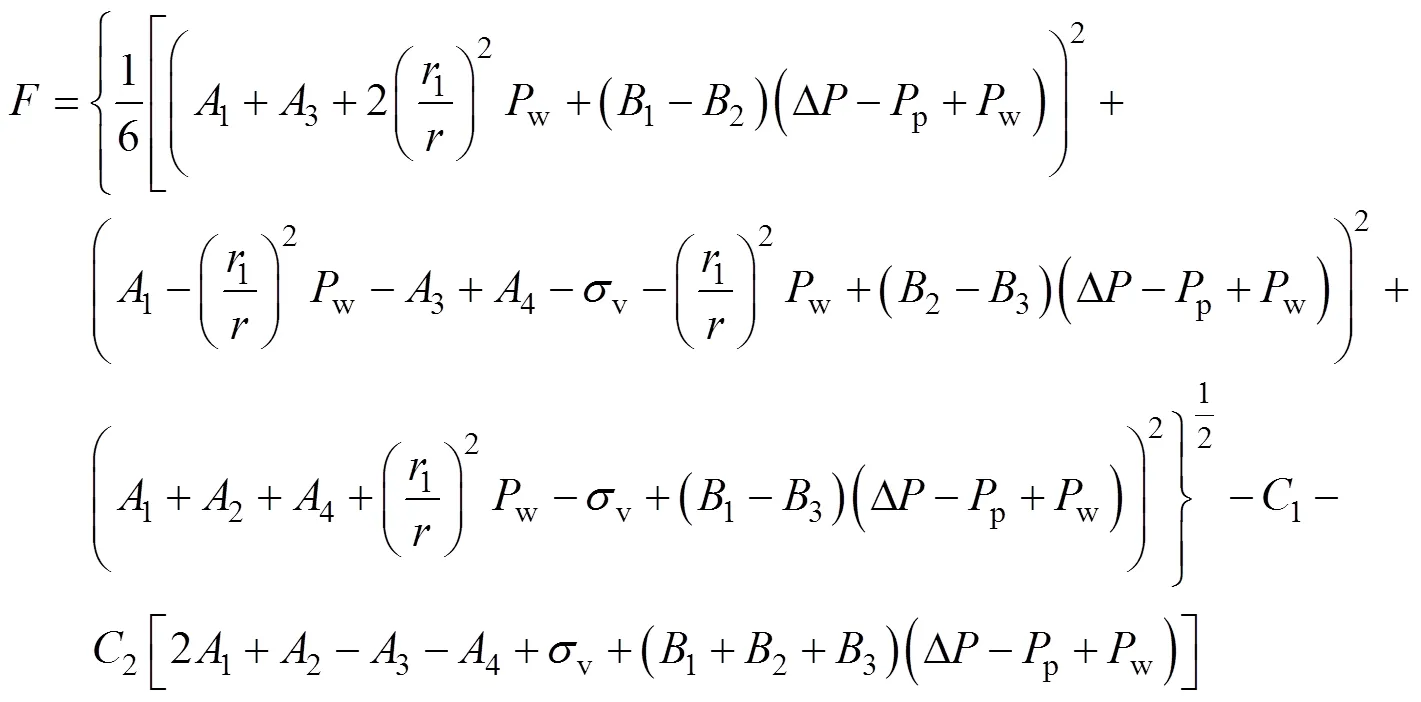
2 降压开采水合物储层应力变化分析

2.1 模拟采用的基本参数

模型计算所选用的参数采用墨西哥湾某处甲烷水合物藏的部分基本参数[18]来分析降压开采水合物过程中近井区储层应力的变化特征。

墨西哥湾某处水合物藏的部分基本参数: 水合物储层温度288 K; 储层初始压力16.9 MPa; 井孔半径0.15 m; 储层垂向原始主应力21.8 MPa; 储层最大水平原始主应力20.45 MPa; 储层最小水平原始主应力19.70 MPa; 储层厚度30 m; Biot有效应力参数0.6; Biot系数1.0; 水合物饱和度0.5; 储层孔隙度0.4; 泊松比0.4; 储层初始渗透率0.2 μm2; 多孔介质压缩系数10–9Pa–1; 水的压缩系数4.6×10–10Pa–2; 储层内聚力1.8 MPa; 内摩擦角30°。其中, 泄油半径100 m。

2.2 水合物储层物性参数及力学性质变化分析

图2、图3分别给出了生产压差3 MPa, 不同生产时间下水合物饱和度分布、储层渗透率分布曲线图。降压开采水合物过程中, 初始水合物储层饱和度受已存自由气体的影响。

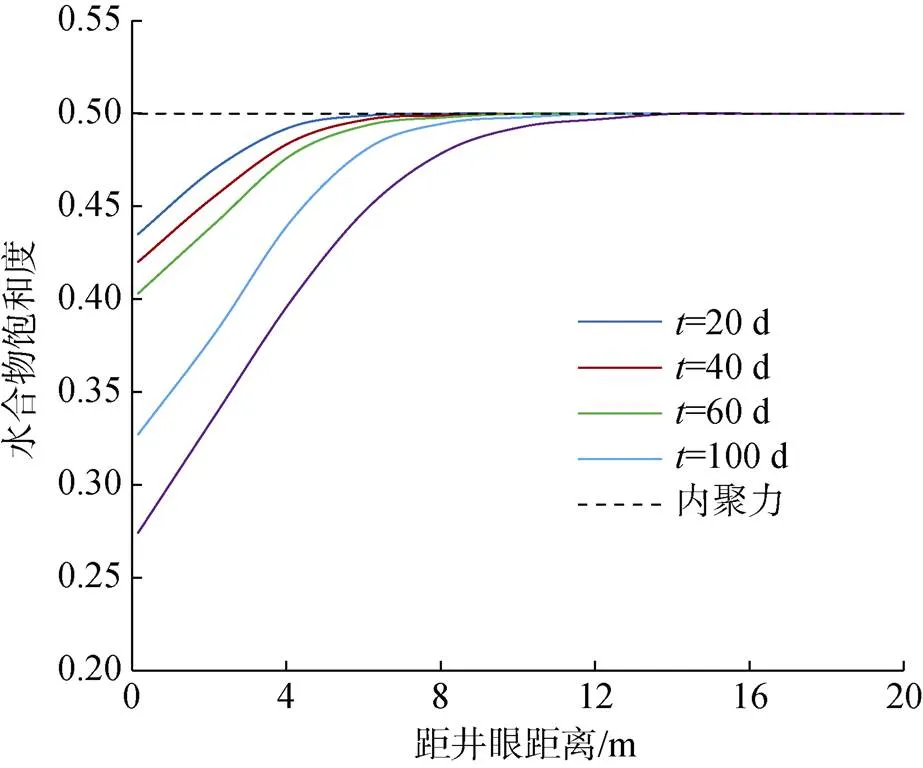
图2 水合物饱和度分布曲线

从图2中可以看出, 由降压开采引起的水合物饱和度变化主要发生在近井区, 在降压开采水合物初期(20 d), 靠近井壁处的水合物饱和度减小的相对缓慢, 这主要是因为原水合物储层内存在的自由气体使得储层内的压力升高, 在一定程度上阻碍了水合物的分解速率, 使得水合物的分解速率减慢; 在较远处, 水合物饱和度趋于稳定。随着时间不断增加(60 d), 储层内的自由气体逐渐减少, 水合物饱和度减小的速度逐渐加快, 这与唐良广等[22]研究的水合物饱和度变化规律相符, 进一步证明了该水合物饱和度变化模型的准确性。

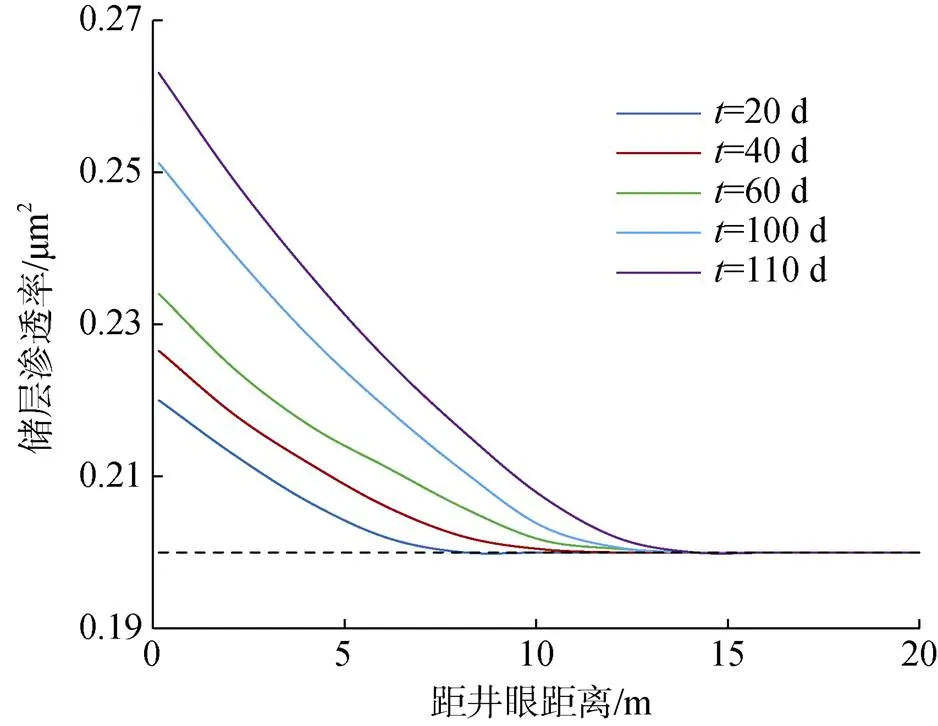
图3 水合物储层渗透率分布曲线

分析图3可以看出, 井壁处的储层渗透率增大的最快, 远离井壁储层渗透率逐渐恢复到原始状态。在水合物分解区, 特别是井壁处水合物分解速率最快, 水合物饱和度减小的最快, 根据式(19)可知, 水合物饱和度和储层渗透率呈反比。因此, 生产时间越长, 水合物饱和度变得越小, 储层渗透率就越大。

2.3 储层渗流附加应力的影响

水合物储层为多孔介质储层, 通过模拟计算得到在生产压差3 MPa, 开井生产100 d后, 研究储层应力过程中考虑渗流附加应力与不考虑渗流附加应力两种情况下对水合物储层径向应力、周向应力进行了对比, 如图4所示。

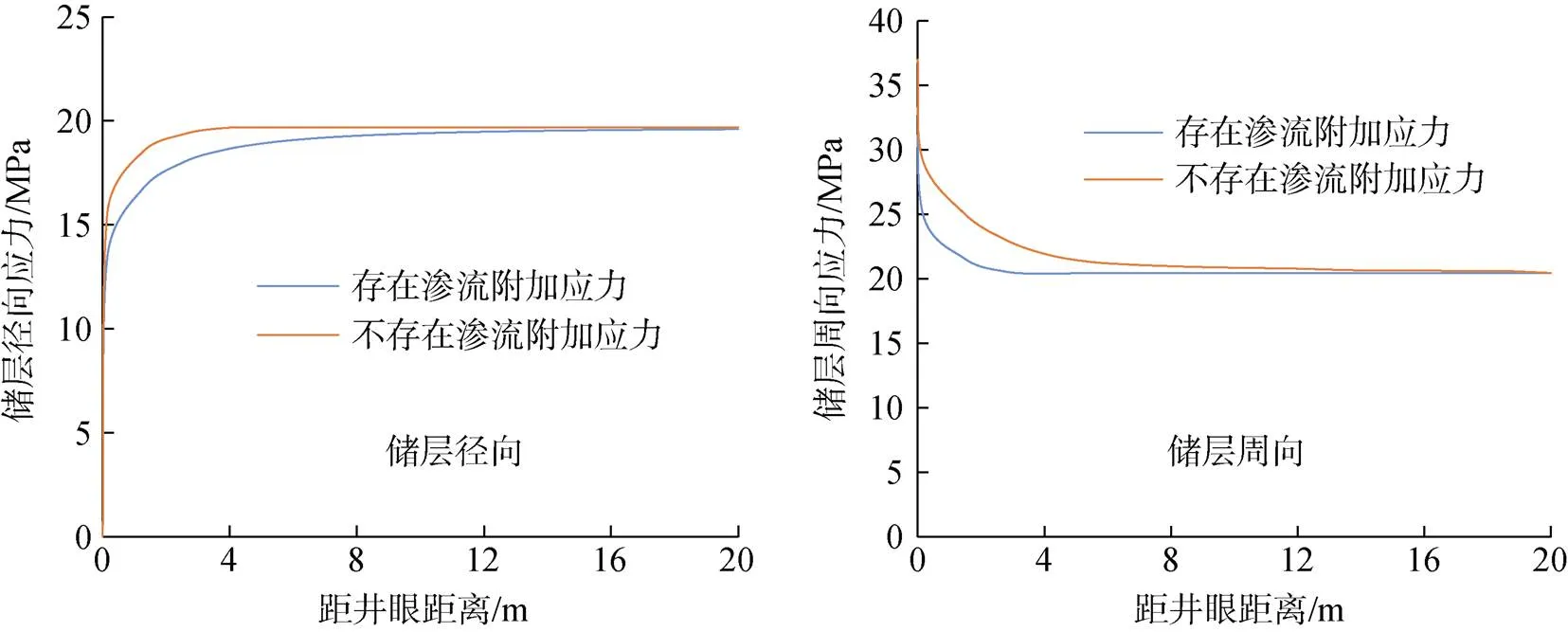
图4 存在渗流附加应力与无渗流附加应力两种情况下储层应力的对比

从图4中可以得出, 考虑渗流附加应力时的储层径向、周向应力小于不考虑渗流附加应力时的储层径向、周向应力。通过对式(2)分析可知, 水合物降压分解过程中, 饱和度逐渐减小, 储层有效孔隙度逐渐增大, 这说明渗流附加应力降低了储层的稳定性。

在井底压力13.9 MPa, 井眼半径0.15 m的条件下, 分析考虑近井区水合物储层渗流附加应力和不考虑渗流附加应力时, 储层所受最大轴向偏应力分布曲线如图5所示。结合图4, 由图5不难得出, 考虑渗流附加应力时储层所受最大轴向偏应力小于不考虑渗流附加应力时储层所受最大轴向偏应力。因此, 在建立水合物储层的力学模型时, 必须考虑渗流附加应力对水合物储层的影响, 以减小预测结果的误差。

图5 储层最大轴向偏应力分布

2.4 水合物储层应力分析

通过降低井底压力, 使水合物储层压力低于其平衡压力, 促使水合物发生分解生成天然气和水。井底压力变化会改变一定区域的原始储层应力, 造成分解区水合物储层发生应力集中, 从而降低水合物储层的稳定性。在降压开采水合物过程中水合物储层径向、周向、垂向应力表现出不同的变化。图6显示了在生产压差3 MPa, 开采时间100 d后, 塑性区水合物储层应力的分布曲线。

通过式(3)不难看出, 水合物储层应力是角度的函数, 储层周向、垂向应力随角度呈周期性变化, 储层径向应力不发生变化。近井区水合物储层中最大、最小应力之间的差值随着距井孔距离的增大逐渐减小, 在井周上某点与水平最大主应力方向的夹角90°或270°方位处, 水合物储层的最大、最小应力之间的差值最大, 即近井区水合物储层所受到的挤压应力最大。根据Drucker-Prager岩石破坏准则, 储层周向、径向应力之间的差值越大, 储层越容易发生剪切破坏。因此, 这两个方位处也是储层最容易发生剪切破坏的位置, 储层发生剪切破坏一般是从井壁处开始的。

图6 储层应力随角度的变化曲线

Drucker-Prager准则认为储层发生的破坏主要是剪切破坏, 根据式(29)进一步说明储层破坏的临界条件。保持其他参数不变, 水合物储层稳定性随生产压差变化的关系图如图7所示。由图7可知, 水合物储层稳定性指数随生产压差的增大而减小。这是因为井底压力越小, 即生产压差越大, 储层有效应力增大越快, 造成储层失稳的可能性就越大; 随着生产压差的增大, 水合物分解速率加快, 储层物性变化越显著。

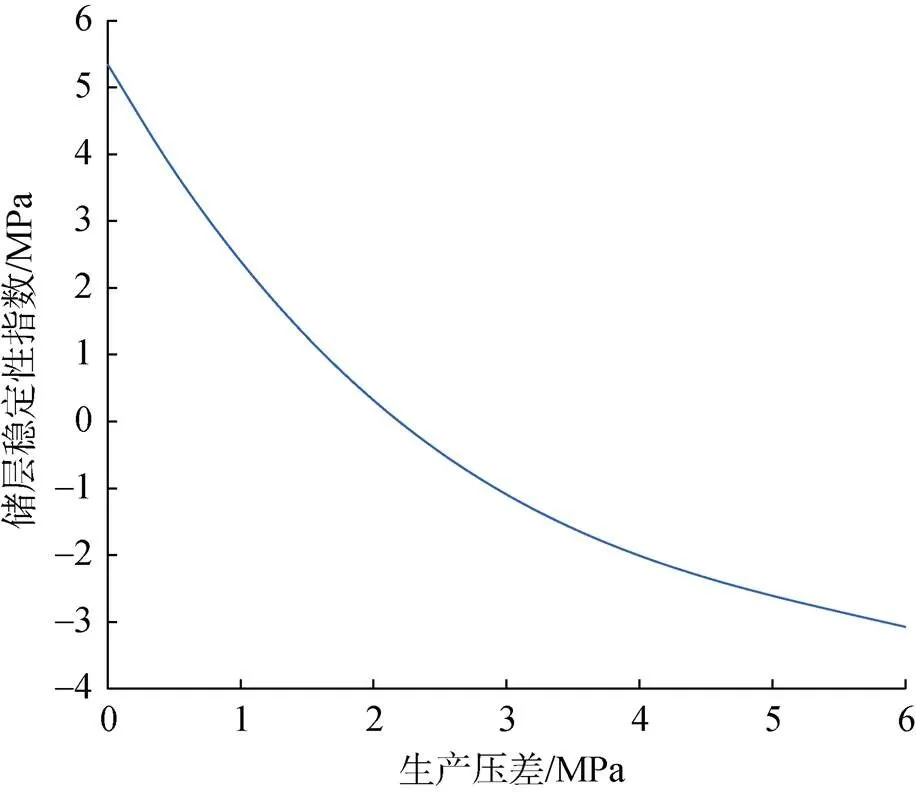
图7 储层稳定性随生产压差变化关系图

通过对图7曲线进行线性回归得到储层稳定性指数与生产压差之间的关系式(30)所示:

= 0.247 3Δ2– 2.803 7Δ+ 5.092 9, (30)

式中:为储层稳定性指数, MPa; Δ为生产压差, MPa。

通过解式(30), 得到水合物储层临界生产压差为2.19 MPa。当生产压差小于2.19 MPa, 水合物储层保持稳定; 相反, 当生产压差大于2.19 MPa, 水合物储层发生剪切强度破坏, 有可能会引起储层出砂。因此, 降压开采水合物过程中, 应保持井底压力大于14.71 MPa。

综合以上分析可知, 在降压开采水合物过程中, 水合物分解区是整个储层稳定性较差的区域。降低井底压力: 一方面, 促进了水合物的分解, 储层内聚力减小, 储层各应力发生改变; 另一方面, 不合理的降压会造成储层发生剪切破坏, 进而影响水合物的有效开采。因此, 在降压开采水合物过程中应保证合理的井底压力。

3 结论

1) 降压开采水合物过程中, 由于水合物发生分解, 分解区储层呈现出弱胶结、低强度、高孔渗的特点, 在不同生产压差下, 近井区储层应力发生了明显的改变, 距井孔较远处储层应力不再发生变化而趋于原始储层应力。说明近井区储层出现应力集中的现象, 井底压力是影响储层稳定性的重要因素。

2) 生产压差越大, 塑性区水合物储层所受轴向偏应力就越大, 井壁处所受轴向偏应力最大, 是整个水合物储层优先破坏的位置。其中, 生产压差2.19 MPa作为降压开采水合物过程中储层发生剪切破坏的临界压差。

3) 有待进一步开展对天然气水合物降压开采过程中储层应力变化分析, 确定水合物储层发生剪切破坏的生产压差的合理临界点, 为今后有效开采天然气水合物奠定一定的基础。

[1] Makogon Y F, Holditch S A, Makogon T Y. Natural gas- hydrates: A potential energy source for the 21st Century[J]. Journal of Petroleum Science & Engineering, 2007, 56(1-3): 14-31.

[2] Moridis G J, Collett T S, Dallimore S R, et al. Numerical studies of gas production from several CH4, hydrate zones at the Mallik site, Mackenzie Delta, Canada[J]. Journal of Petroleum Science & Engineering, 2004, 43(3-4): 219-238.

[3] Sloan E D. Clathrate hydrates of natural gases[J]. Journal of the American Chemical Society, 1998, 120(43): 11212.

[4] Ji C, Ahmadi G, Smith D H. Natural gas production from hydrate decomposition by depressurization[J]. Chemical Engineering Science, 2001, 56(20): 5801-5814.

[5] Wang Yi, Li Xiaosen, Xu Wenyue, et al. Experimental investigation into factors influencing methane hydrate formation and a novel method for hydrate formation in porous media[J]. Energy and Fuel, 2013, 27(7): 3751- 3757.

[6] 喻西崇, 吴应湘, 安维杰, 等. 开采地层中的天然气水合物的数学模型[J]. 天然气工业, 2004, 24(1): 63-67. Yu Xichong, Wu Yingxiang, An Weijie, et al. Mathema­tical model to recover gas hydrate from formations[J]. Natural Gas Industry, 2004, 24(1): 63-67.

[7] Ahmadi G, Ji C, Smith D H. Numerical solution for natural gas production from methane hydrate dissociation[J]. Journal of Petroleum Science & Engineering, 2004, 41(4): 269-285.

[8] Aadnoy B S, Chenevert M E. Stability of highly inclined boreholes[J]. SPE Drilling Engineering, 1987, 2: 364-374.

[9] Fjar E. Petroleum Related Rock Mechanics[M]. Amsterdam: Elsevier, 2008.

[10] 刘玉石, 黄克累. 孔隙流体对井眼稳定的影响[J]. 石油钻探技术, 1995, 23(3): 4-6. Liu Yushi, Huang Kelei. Effects of pore fluids on borehole stability[J]. Petroleum Drilling Techniques, 1995, 23(3): 4-6.

[11] 阎铁, 李士斌. 深部井眼岩石力学理论与应用[M]. 北京: 石油工业出版社, 2002. Yan Tie, Li Shibin. Deep Borehole Rock Mechanics Theory and Applications[M]. Beijing: Petroleum Industry Press, 2002.

[12] 张建国, 杜殿发, 侯建, 等. 油气层渗流力学[M]. 东营: 中国石油大学出版社, 2010. Zhang Jianguo, Du Dianfa, Hou Jian, et al. The Oil and Gas Flow through Porous Media[M]. Dongying: China University of Petroleum Press, 2010.

[13] Jacob B. Dynamics of Fluids in Porous Media[M]. New York: American Elsevier Pub. Co., 1972.

[14] Masuda Y, Kurihara M. A filed scale simulation study on gas productivity of formation containing gas hydrates[J]. Proceedings of the Fourth International Conference on Gas Hydrates, 2002, 15(6): 622-627.

[15] 张新红, 秦积舜. 低渗岩心物性参数与应力关系的试验研究[J]. 中国石油大学学报: 自然科学版, 2001, 25(4): 56-57. Zhang Xinhong, Qin Jishun. Relation of Ground Stress with the Properties of Low Permeable Core[J]. Journal of China University of Petroleum (Edition of Natural Science), 2001, 25(4): 56-57.

[16] 沈海超. 天然气水合物藏降压开采流固耦合数值模拟研究[D]. 青岛: 中国石油大学, 2009. Shen Haichao. Fluid-solid coupling numerical simulation on natural gas production from hydrate reservoirs by depressurization[D]. Qingdao: China University of Petroleum, 2009.

[17] Nazridoust K, Ahmadi G. Computational modeling of methane hydrate dissociation in a sandstone core[J]. Che­mical Engineering Science, 2007, 62(22): 6155-6177.

[18] Freij-Ayoub R, Tan C, Clennell B, et al. A wellbore stability model for hydrate bearing sediments[J]. Journal of Petroleum Science & Engineering, 2007, 57(1): 209-220.

[19] 冉启全, 顾小芸. 油藏渗流与应力耦合分析[J]. 岩土工程学报, 1998, 20(2): 69-73. Ran Qiquan, Gu Xiaoyun. Coupling analysis of multiphase flow and stress for oil reservoir[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 69-73.

[20] Makogon Y F. Hydrates of hydrocarbons[J]. Penn Well Books, 1997, 610(52): 50-62.

[21] Kimoto S, Oka F, Fushita T, et al. A chemo-thermo- mechanically coupled numerical simulation of the subsurface ground deformations due to methane hydrate dissociation[J]. Computers & Geotechnics, 2007, 34(4): 216-228.

[22] 唐良广, 冯自平, 李小森, 等. 天然气水合物降压开采的数值模拟研究[C]//中国科学技术协会.中国工程热物理学会多相流学术会议. 北京: 中国科学技术协会, 2006: 691-698. Tang Lianguang, Feng Ziping, Li Xiaoshen, et al. Numerical Simulation on Natural Gas Production from Hydrate Reservoirs by Depressurization[C]// Science and Technology Conference of Chinese. Multiphase Flow Academic Conference of Chinese Society of Engineering Thermophysics. Beijing: Science and Technology Conference of Chinese, 2006: 691-698.

Geomechanical stress law analysis of hydrate reservoir for gas hydrate production by depressurization

JIN Hao, ZHANG Jun-bin, HE Yu-fa

(Deepwater Engineering Technology Center of CNOOC (China) Co., Ltd., Shenzhen 518000, China)

A model combining linear porous elasticity and rock mechanics knowledge is developed to analyze the geomechanical stress of the hydrate reservoir and assess the wellbore stability during depressurization. The proposed model considers the original reservoir stress, pore pressure, seepage additional stress, and depressurization of hydrate mining during the process of hydrate saturation change. This model is applied to the case of the Gulf of Mexico, where the hydrate reservoir basic parameters have been publicly published and depressurization of the hydrate mining reservoir has been simulated and analyzed. Results show that the effect of bottom hole pressure is the dominant factor affecting the formation of reservoir stress. Moreover, reservoir stress significantly affects the wall. Therefore, the wall is the location that is most prone to shear failure. To assess the wellbore stability during the process of depressurization, the production pressure difference of the hydrate reservoir must be <2.19 MPa.

depressurization; gas hydrate reservoir; seepage additional stress; hydrate saturation; critical production pressure differential; wellbore stability

Oct. 31, 2019

TE319

A

1000-3096(2020)11-0001-09

10.11759/hykx20191031002

2019-10-31;

2019-12-10

国家重点研发计划项目 (2016YFC0304000)；国家重点研发计划课题 (2016YFC03044007)；国家重点研发计划课题 (2018YFC0310205)

[The National Key R&D Program of China, No. 2016YFC0304000; The National Key R&D Program of China, No. 2016YFC03044007; The National Key R&D Program of China, No. 2018YFC0310205]

金颢(1984-)，男，广东深圳人，高级工程师，主要从事钻井、完井、测试、水合物等领域相关内容研究，电话：15899755760，E-mail：jinhao@cnooc.com.cn

(本文编辑: 刘珊珊)