钢悬链式立管加速度试验及仿真

朱擘， 黄维平， 姚兴隆， 刘娟， 付雪鹏

(1.中国海洋大学 山东省海洋工程实验室，山东 青岛 266071； 2.江苏海洋大学 土木与港海工程学院，江苏 连云港 222005； 3.青岛农业大学 建筑工程学院，山东 青岛 266009)

钢悬链式立管是海洋深水开发的重要装备，其涉及顶部运动、波浪及水流荷载、涡激振动、刚体摆动、管土相互作用等多种荷载模拟、影响分析等要求。本文主要对考虑两向涡激振动模型进行校核工作，该模型能从经验模型出发，通过简易公式实现，具有相对较好适用前景。

Cardoso等[1]提出一种带水动力阻尼器钢悬链线的立管结构优化设计方法，希望可减少立管压缩波动，阻尼器可通过GBNM方法确定其分布。Min Lou等[2]推求静态几何非线性方程求解具有悬链线立管特点的顺应式立管(CVARs)响应，以适应于深水开发。Lou等[3]推求具有悬链线特点的顺应式立管垂向作用下结构不稳定特点。计算表明结构存在模态耦合，存在不稳定区间及耦合等问题加剧损伤等情况。Shoghi等[4]研究提出一套新方法研究钢悬链线立管沟槽效应对结构损伤的影响。研究表明船舶低频运动等荷载对结构响应影响不可忽视。Kim等[5]采用Kirchhoff′s理论建立悬链线等立管动态方程。方程可考虑拖曳力及内部流体作用。对于杆件模型，他们采用线性方法分析内部流体对结构型态影响。Yin等[6]利用时域VIV预测模型对CF较小情况VIV响应进行估计，在此基础上与实测响应进行比较。Wang等[7]采用有限元方法求解侧向位移及弯矩，研究了环空间隙、海洋深度、平台偏移和摩擦系数对结构的影响。Monsalve等[8]提出简化疲劳计算方法估计结构短期疲劳响应。以钢悬链线立管做算例，将简化算法与详细算法进行对比分析，验证简化算法有效。Thorsen等[9]研究立管内部流动对结构VIV及疲劳损伤的影响。Xue等[10]对柔性立管受剪切振荡流VIV响应影响进行分析，讨论周期及最大流速对振动响应影响。

相对而言，Cable3D程序试验校核数据还较少。本文在试验基础上，对结构加速度响应及其振动特点进行研究。通过振动平衡位置、标准差及最值等响应验证立管非锁定区间涡激振动模型的可靠及稳定性。相比之前研究，本文侧重于满足近似弗汝德相似条件下，验证结构响应计算可靠性。本文希望在与试验对比及验证Cable3D计算可靠等方面完善一点工作，为后续相关计算开展提供一点基础

1 SCR柔性梁模型

按照牛顿第二定律及作用荷载动量矩定律，可获取ds长度梁作用平衡方程[11]:

(1)

(2)

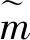
(3)

(4)

式中：B为弯曲刚度；H为扭矩。假定不考虑扭矩及外力矩作用，结合式(1)、(2)，结构基本方程：

(5)

(6)

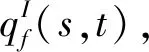
(7)

式中M为质量矩阵。顶部节点及海底锚固点约束所有自由度，与土体接触段采用弹性支撑刚度模拟管土相互作用。

2 VIV经验模型

涡激振动研究方法集中于实验、尾流振子及流体仿真3种形式。本文计算主要采用尾流振子及公式考虑相互作用2种方法。其优势是代价小、程序实现较容易。

1)Iwan and Blevins经验模型。Orcaflex程序中振子模型种类较多[12-13]，在众多模型中，Iwan and Blevins经验模型相对而言模拟幅度接近试验数据。其他模型主要存在在多工况下难以完全匹配试验数据，计算参数需要调整等情况。

2)考虑两向运动VIV模型。

① 涡激升力。涡激升力公式较简易[11]，非锁定区考虑相互作用，公式修正为：

(8)

k1=1/2CLρD

(9)

(10)

式中：D为直径；U为速度；Ur为相对速度；fs为Strouhal数。

②拖曳力。

在非锁定区域，平均及脉动拖曳力[11]为：

(11)

k2=1/2CDρD

(12)

(13)

3 试验分析

3.1 试验工况

本文主要目标是验证程序模型计算精度，通过对比Cable3D数据与试验及Orcaflex数据，验证计算是否可靠，为后续工作做一点准备。试验主要采用0.12～0.30 m/s，6个工况加速度传感器数据。图1～2是模型及设备连接[12-16]。

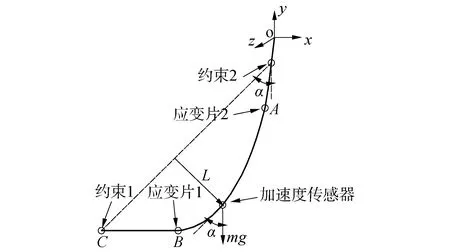
图1 试验立管模型Fig.1 Model figure of test riser

表1 立管原型及模型Table 1 Prototype and model parameters of riser

3.2 试验程序

试验主要通过安装在触底点附近的加速度传感器来实现信号输出。表2给出试验工况。

图2 试验连接Fig.2 Figure of test connection

表2 试验方案[12-16]Table 2 Plan for test[12-16]

3.3 试验分析

图3是测试得到试验一0.12 m/s结构20～80 s加速度响应曲线。选取中间区域可减弱测试启动段及结束段对结构影响。

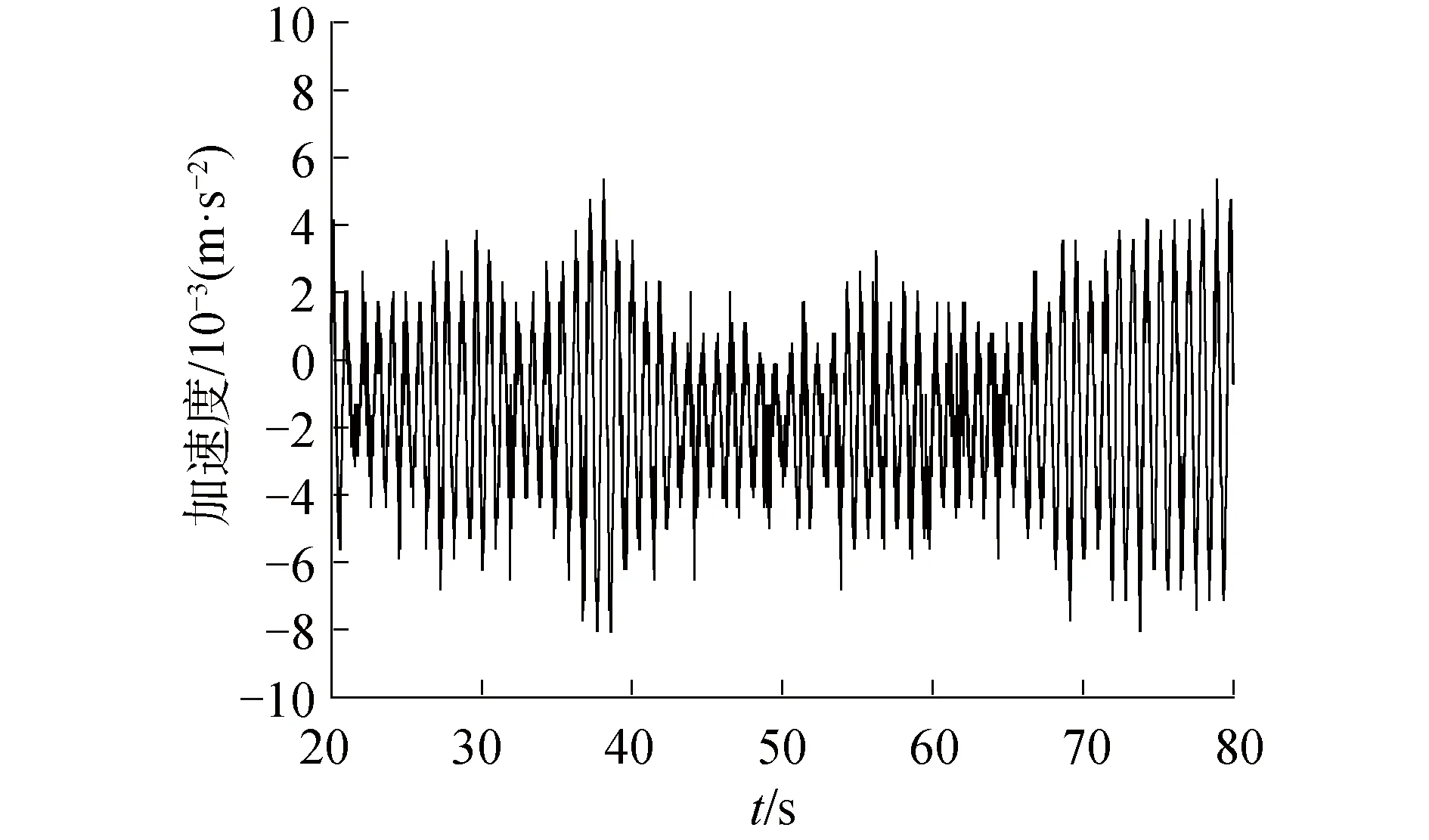
图3 试验一0.12 m/s加速度响应曲线[12-16]Fig.3 0.12 m/s acceleration time history of test 1[12-16]

上述时程曲线及其数据处理之后的平衡位置、标准差、最值等可做数值模拟校核依据。其中平衡位置体现振动偏动情况、标准差体现结构振动强弱、最值体现结构振动幅度。通过上述偏离开平衡位置、振动强度及幅度可基本判断振动模拟相似程度。而在模拟之前，需要对速度进行一定修正过渡，考虑水上悬垂速度及水下实际速度，对其分布进行一定修订工作，使数据接近试验情况。

试验显示：最值及振动区间增加说明涡激振动等横向作用使结构响应逐步增加，结构处于非锁定区间。振动区间在0.19 m/s有所减低，其他基本呈现增加情况。试验1～2数据最值见表3～4，标准差及最小值变动情况见表5～6。

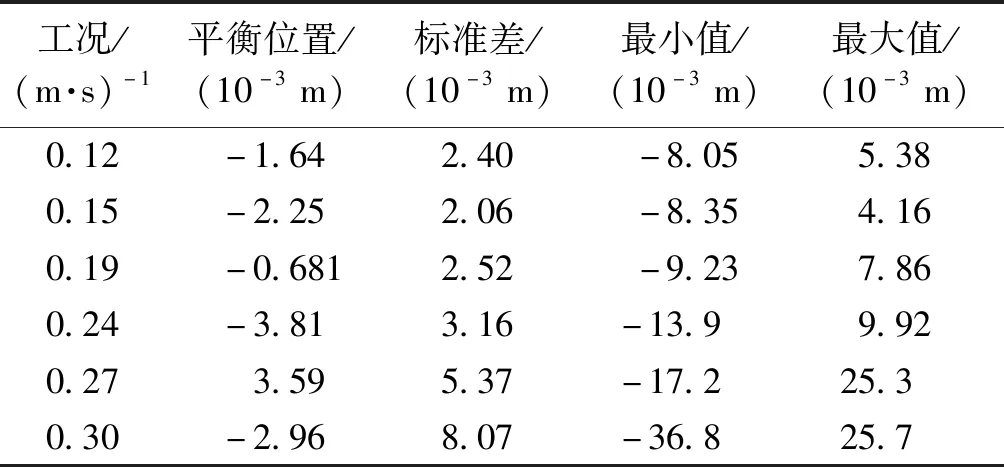
表3 试验一VIV数据后处理Table 3 Post processing of VIVfor test 1

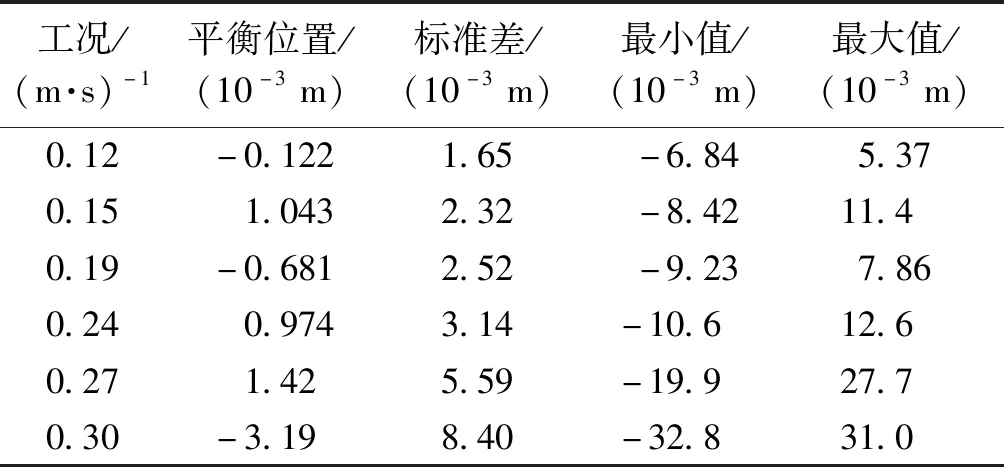
表4 试验二VIV数据后处理Table 4 Post processing of VIV for test 2

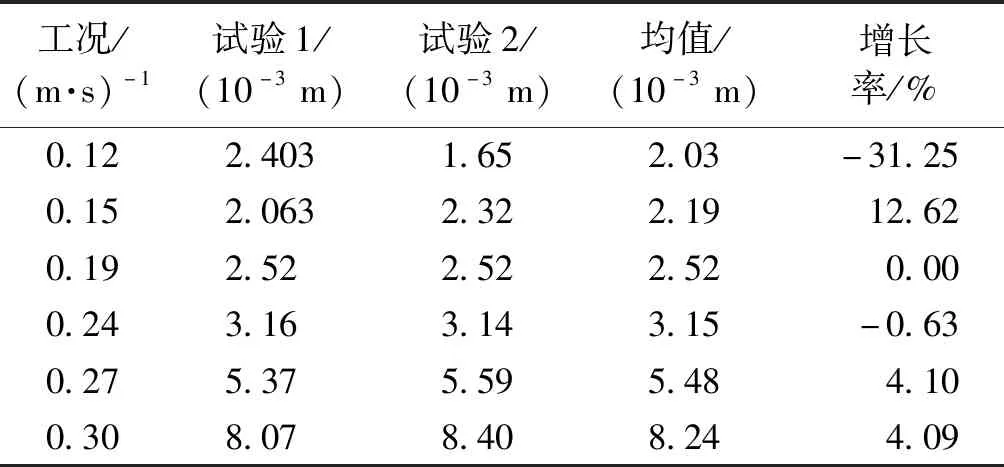
表5 试验波动标准差变动情况Table 5 Fluctuation st of test conditions

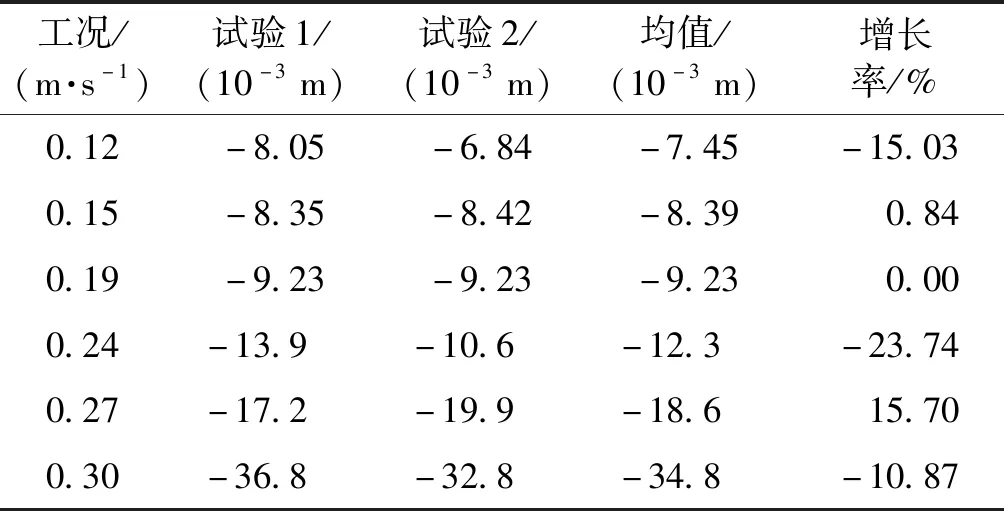
表6 试验最小值变动情况Table 6 Fluctuation minimum of test condition

从振动标准差及最值角度分析，0.12～0.19 m/s，0.19～0.24 m/s及0.24～0.30 m/s存在明显区间。对比平衡位置、振动标准差及最值区间等情况，在0.12、0.24 m/s附近三者都存在变动情况显著情况，图4～6所示。而这种变动在0.25 m/s附近出现大幅度偏离平衡位置、振动标准差、最值及区间大幅度增加。

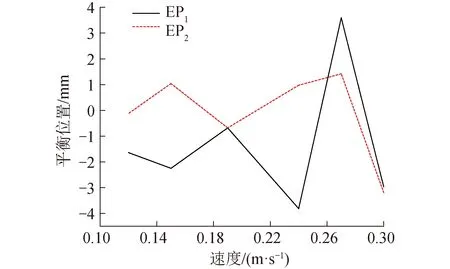
图4 平衡位置与水流关系图Fig.4 The relationship of equilibrium positionand flow velocity

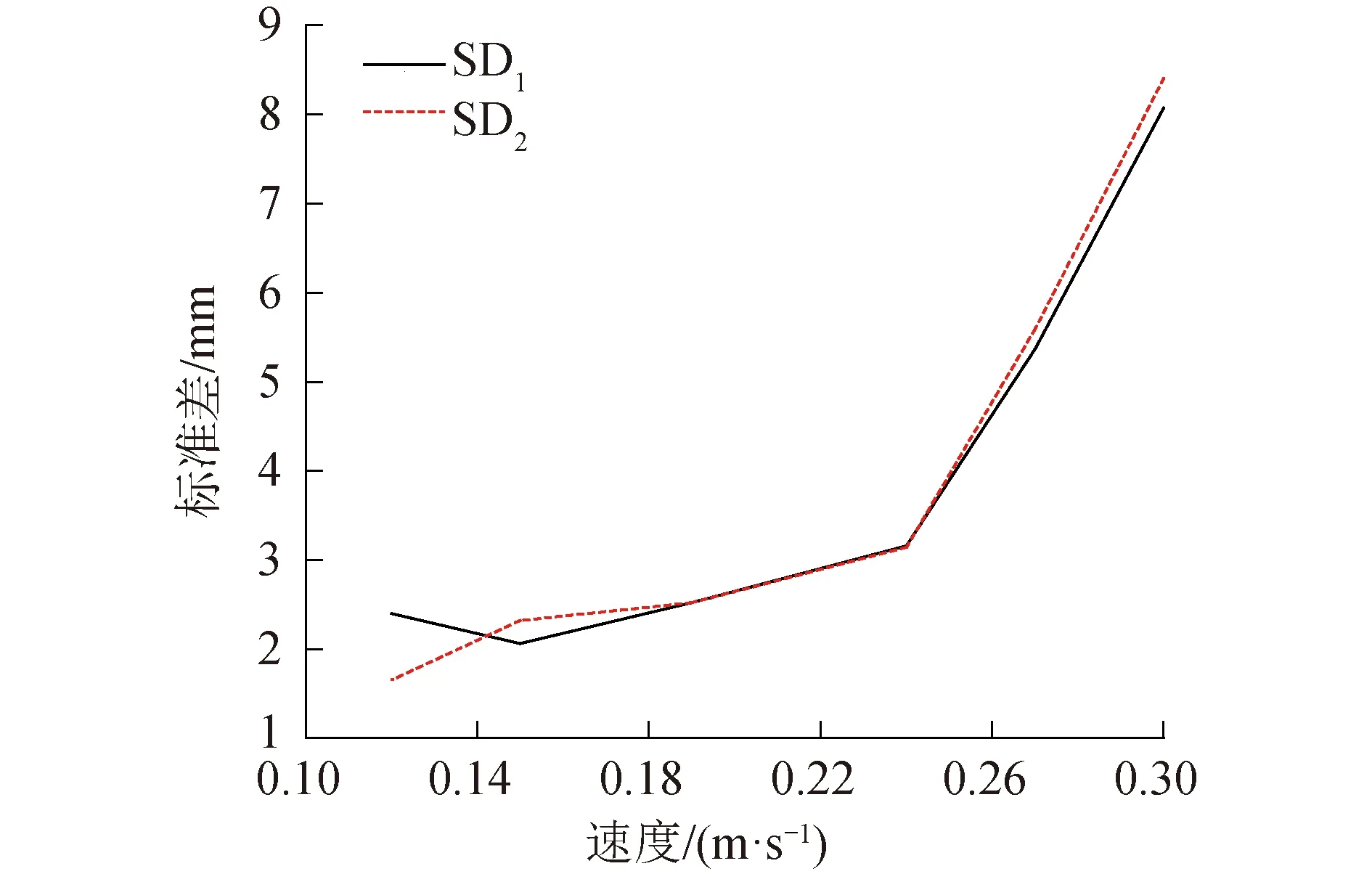
图5 标准差与水流关系Fig.5 The relationship of standard deviation and flow velocity

图6 区间及最值与水流关系Fig.6 The relationship of extreme value & variation range and flow velocity

从横向自振频率表7及涡激振动计算fs=stU/D可知道，试验0.15 m/s及0.25 m/s存在涡激振动频率接近自振频率的情况，表现是响应大幅度变动。虽然共振在0.12 m/s时有所体现，然而在较高速度时，情形更加显著。

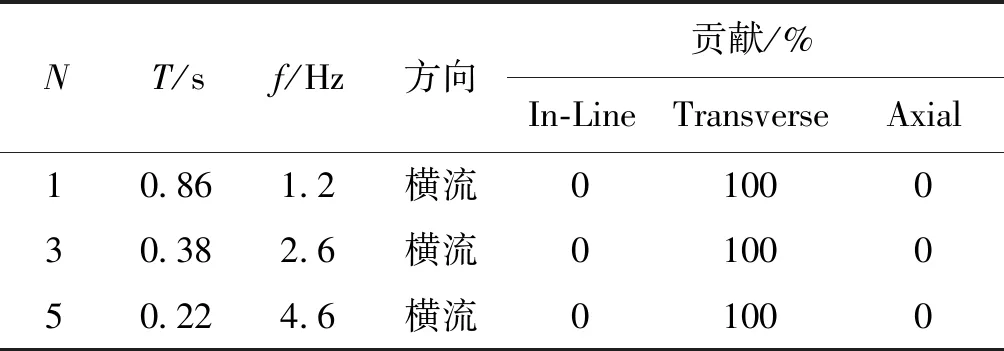
表7 Orcaflex自振求解[12-16]Table 7 Natural vibration caculated by Orcaflex[12-16]

4 数值仿真

4.1 基本参数

本文Cable3D数值模拟的主要目标是校核计算精确度，通过数据与试验对比分析明确计算精确度。试验基本采用弗汝德相似准则，加速度传感器安装在SCR管触底区域1、5 m附近。Cable3D模型，其所在节点为12th，图7所示。通过基本模型对应试验及数值模拟数据，明确计算精确度之后，可获取结构在不同荷载及不同节点响应特点。本文存在的主要问题是结构测点的单一，缺乏更全面的校核依据。在对单一测点数据，主要通过时程曲线相似、振动平衡、振动强度及振动幅度等进行结构响应对比。

图7 SCR线型图[12-16]Fig.7 The equilibrium position of SCR[12-16]

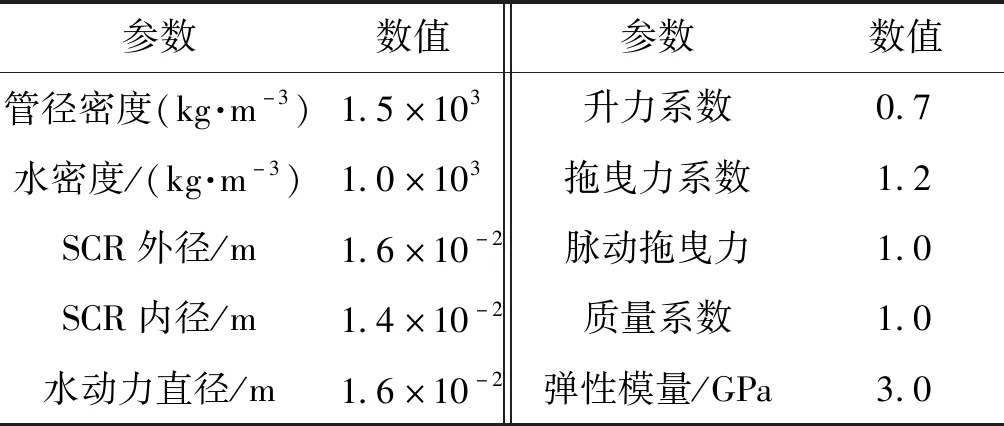
表8 SCR基本模拟参数[12-16]Table 8 SCR physical parameters[12-16]

试验PVC管长3.3 m。流线段1.5 m。悬挂点到水底高度0.85 m。结构质量可由管径密度、内外径等参数求取。浮力等参数需要按临界阻尼等进行调整。结构拉伸及弯曲刚度等按材料力学公式计算不做大幅度调整[11-16]。荷载步0.02，计算时间100 s。计算误差及其他参数采用默认。对Orcaflex而言，尾流振子模型参数不做大幅度调整。其余参数与Cable3D参数相似。值得注意的是结构悬链线形状不是完全依靠自身荷载形成(主要外荷载弯曲形成)，在水面上还有悬垂段。在数值模拟时，除了需要调整速度分布之外，还需要判断结构线型是否能符合试验情况(对比锚定点、触底点、悬挂角及计算总长等参数)。同时，需要对横流向响应进行相对更多校核判定。

4.2 数值模拟分析

图8是Cable3D模拟及试验与Orcaflex模拟及试验对比分析情况。需要补充的是，本文Orcaflex模拟仅做对比分析，指出结构计算模拟一般精确度。因为计算准确依靠模型及参数调整。而计算精确度可通过这种计算简易给出。由于PVC管型式形成不完全依靠结构自重等自身荷载，基本还依靠外荷载弯曲。在现有数值计算模拟时候不能完全以模型参数输入。现有Cable3D以临界阻尼做调整依据依据，考虑质量及刚度折减。某种程度上主要依靠质量及浮力调整，通过调整质量项及浮力项进行线型调整。总体而言，对6个工况以上述原则或者方式进行调整线型之后，计算在一定程度上符合试验曲线。曲线差异主要来自于叠加差异(结构涡激振动等荷载频率、幅值及相位等的叠加区别)，及荷载模型差异(各种荷载计算与试验实际荷载模型等还有所差异)。结构模拟具有一定可靠性。

图8 0.12 m/s工况加速度时程曲线Fig.8 Acceleration time history of 0.12 m/s

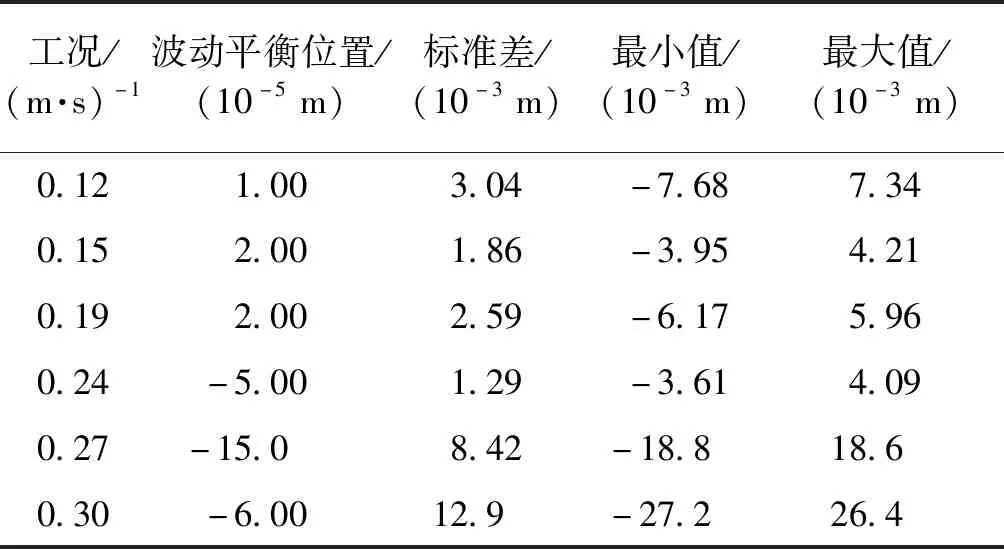
表9 Cable3D VIV后处理Table 9 Post processing of VIV for Cable3D

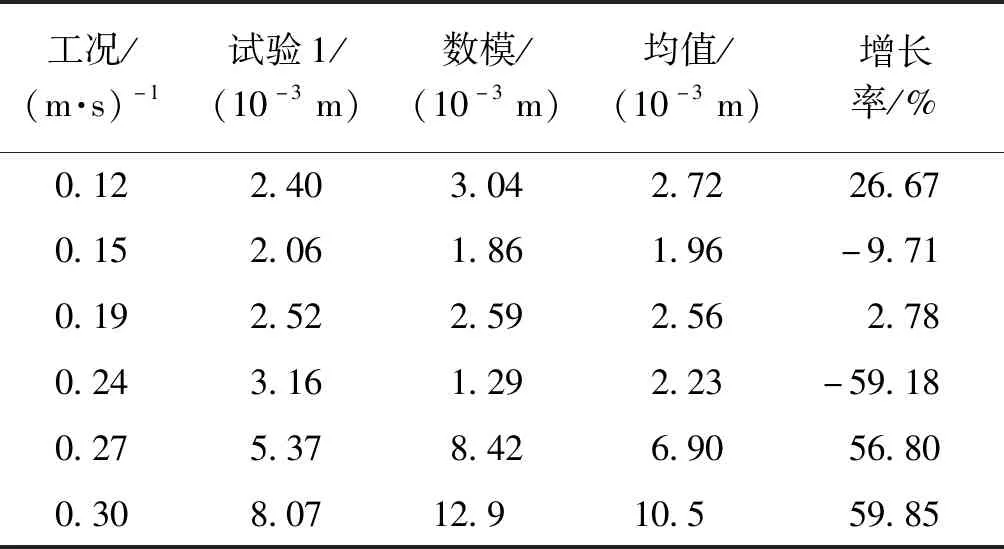
表10 试验工况波动标准差Table 10 Fluctuation st of test conditions

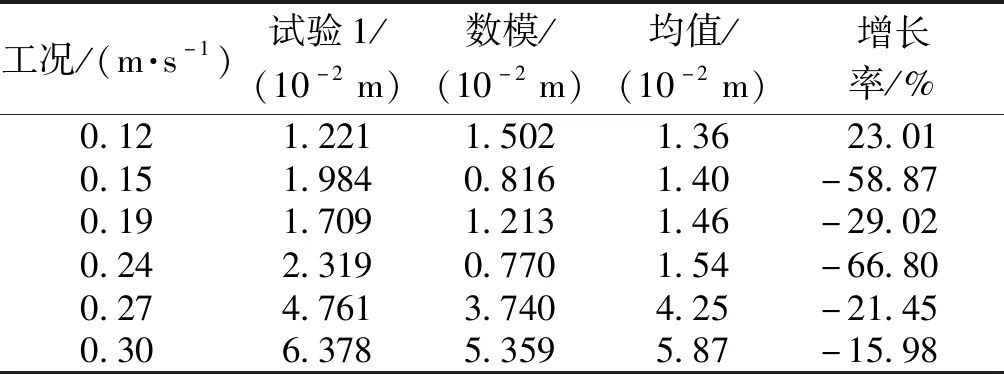
表11 试验工况波动区间Table 11 Fluctuation of test condition

最值及振动区间增加说明涡激振动等横向作用使结构响应逐步增加，结构处于非锁定区间。对结构数值模拟而言，在0.15 m/s及0.24 m/s关键节点数据大幅度变动特点可获取是其最大优势，如表5及表10，但差距相比较2组试验之间差距较明显，是其主要的不足。在0.24 m/s之后，结构振动标准差及最值迅速增加也可在数值模拟中得以体现，图9所示。

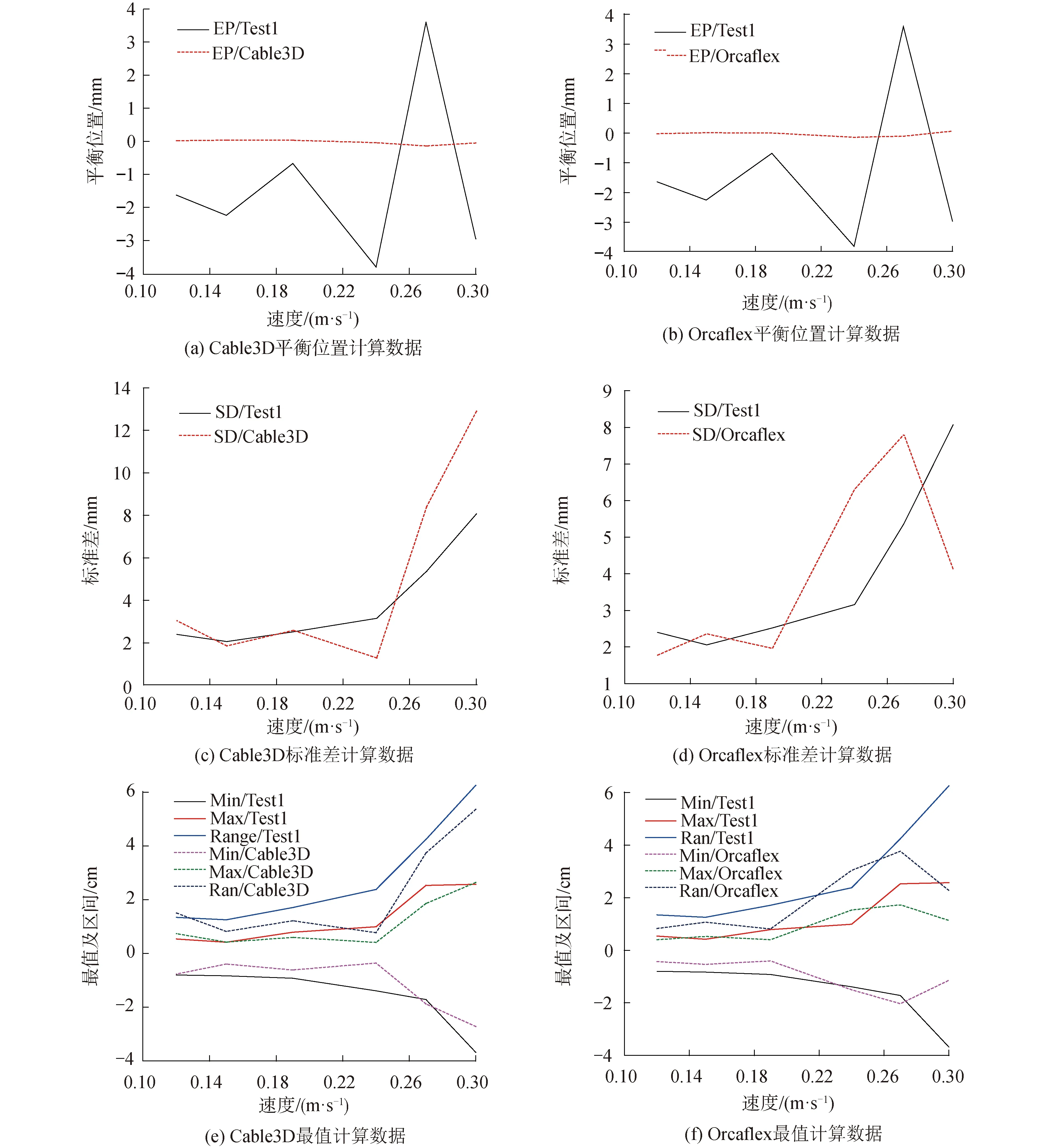
图9 计算工况平衡位置、标准差、最值及振动区间与速度曲线Fig.9 The relationship of equilibrium position, standard deviation, extreme value, variation range and flow velocity

综上，Cable3D数值模拟振动标准差、最值及区间上总体趋势与试验相符，且在0.15 m/s及0.24 m/s关键节点上能反应出差异最大，迅速增加等特点。表明Cable3D在总体及局部关键节点数值计算能力较优秀。但与试验差距不容忽视，程序模拟还存在进一步改善需求。而这种差异与振动平衡位置不发生明显偏离开也许相关。对比而言，在本例中Orcaflex-IWAN AND BLEVINS模型计算数据图9所示。在振动标准差及最值，模拟精确度与Cable3D计算相当。以此佐证结构数值计算精确度。

对比图4～6及图9可知，结构相似程度在最值及区间上较好得以符合，但在振动标准差及平衡位置上还有较显著的差异。结构振动幅值相似代表结构在振动最值能满足一定精度要求，但振动程度及平衡位置差异使结构在计算相应强度数据时还存在一定差距。而这种差距对于涡激振动及其疲劳损伤是不可忽略的。这是计算不足及改进的空间。值得继续研究探讨。

5 结论

1)多工况计算数据显示在加速度时程、最值及区间，现有计算能相对较好满足要求，具有一定可靠及稳定性。在振动平衡位置、标准差等反应结构振动频率及其强度等内容还存在一定差距。

2)振动平衡位置代表结构净偏动，立管偏动有可能会有碰撞接触等情况，而振动标准差与振动频率及其损伤息息相关。而现有模拟存在频率不完全符合，即使频率差异小，但频谱幅值也不完全相似问题。

3)本次试验0.12～0.30 m/s属于非锁定区间，存在0.12～0.15 m/s及0.24～0.27 m/s附近存在主要的频率，涡激振动与自振存在一定共振。表现是结构振动标准差增加、最值及区间迅速增加。

4)Cable3D数值计算能够模拟计算整体趋势及节点信息。Orcaflex计算显示数值模拟与Cable3D精确度接近。但是在幅度上与试验节点还有一定差距。总体而言，数值模拟计算存在幅值易实现，频率及频谱幅值符合较难及存在平衡偏动等情形。