大学生近年来公共数学成绩分析

齐畅 章叶璐 晏建学

摘 要：学生成绩是衡量学生对课程的掌握情况及教师的教学效果最直接的指标，传统的成绩分析方法是按分数段划分并根据正态分布计算平均成绩和方差。本文主要从正态分布模型检验及聚类分析两方面入手，利用SPSS软件对财经大学2010学年至2017学年部分班级公共数学成绩进行分析，更科学、合理地反映学生对课程的掌握情况，并检验教师的教学效果。

关键词：正态模型檢验 聚类分析 SPSS

基金项目：本文为“第十三届云南财经大学本科生科研训练计划（SRTP）（项目编号47《云南财经大学近年来公共数学成绩聚类分析》）”项目成果。

本文以2010～2017级部分授课班级成绩为例，数据包括学号、姓名、班级编号、课程名称、教学老师、年级、学生总成绩等。数据情况如下：

首先检验学生成绩是否服从正态分布，然后用聚类分析功能对学生成绩进行分析，并检验不同班级、年级、教师之间学生成绩分布差异是否明显，同一老师所带不同班级、不同年级学生成绩差异是否明显，不同老师不同学院不同班级学生成绩差异是否明显，不同年级之间学生成绩差异是否明显。用聚类分析弥补传统按分数段划分及根据正态分布计算平均成绩和方差的不足，更加科学、合理地反映学生对课程的掌握情况及教师的教学成果。

1 对数据分课程进行正态分布模型检验

将2010～2017级的概率论与数理统计（理工类）、微积分（经管类）、微积分（理工类）、线性代数（经管类）、线性代数（理工类）这五门不同的公共数学课程作为分类的依据。

分别对上述课程的学生成绩进行正态分布模型检验。按照“分析-描述统计-探索”的步骤进行操作，将“成绩”作为因变量，得到输出结果（详见附录）。对数据的正态性进行拟合优度检验，首先进行“数据-加权个案”操作，再由“分析-非参数检验-卡方”进行操作，将“成绩”作为因变量，得到输出结果（详见附录）。

从输出结果中，可以看到各个课程的成绩都没有均匀地分布在某个特定的区间内，而是存在有很多偏离区域很大的点。同时，可以看到各个课程的成绩渐进显著性均为0，而卡方拟合优度检验中，该项值小于0.05即视为不满足预期频数，因此可以得出：成绩没有服从正态分布。

2 采用K-Means聚类对成绩分课程进行聚类分析

经过多次尝试，最终确定聚类数目为3类，以下进描述聚类数目为的聚类结果。

将上述不同课程的学成成绩进行聚类分析。按照“分析-分类-聚类”步骤操作，将“成绩”作为变量，并将聚类数设置3，勾选“保存”中的“聚类成员”“与聚类中心的距离”项目和“选项”中的“每个个案的聚类信息”项目，得到输出结果。

从输出结果中以“概率论与数理统计（理工类）学生成绩聚类分析结果”为例可以看到，三个类的聚类中心点，分别是29、63、80。最终聚类中心间的距离，第一类与第二类的距离为34.527，第一类和第三类之间的距离为51.458，第二类和第三类之间的距离为16.931。

从输出结果还可以看出，在以63为聚类中心点的第二类数据样本数是最多的，而以80为聚类中心点的第三类数据样本数次之，以29为聚类中心点的第一类数据样本数最少。

纵观另外四组输出结果，除了微积分（理工类）和线性代数（经管类）之外，微积分（经管类）和线性代数（理工类）均符合这样的规律。因此我们将对数据进行分课程、年级、老师进行聚类分析，以期得到一个普适的规律。

3 采用K-Means聚类对成绩分课程、年级、老师进行聚类

通过2010～2017年公共数学学生成绩，进行分课程、老师、年级，再对每组数据进行聚类分析。具体操作步骤如上所述，得到输出结果：当以课程、年级、老师作为分类的依据，对学生成绩以3个类进行聚类时，基本上刚好可以划分为不及格，刚及格，高分这三个类别。其中，不及格的聚点在8～56之间，其中33为众数。及格的聚点在60～73之间，其中62、64为众数。高分的聚点在75～87之间，其中77为众数。自2010年起到2017年的八年中，不及格的学生成绩虽有略微提高，但是变化不大。及格的学生成绩则变化较大，提升了6～7分。高分组的学生成绩比较稳定，上下浮动不大。同时从输出结果中可以看到教师的不同对学生成绩的分布并无太大影响。

4 采用K-Means聚类对成绩分课程、老师进行聚类

由于考虑到不同老师的教学方法的不同，将所采集到的数据分老师、课程再次进行聚类分析。具体操作步骤如上所述，得到输出结果如下：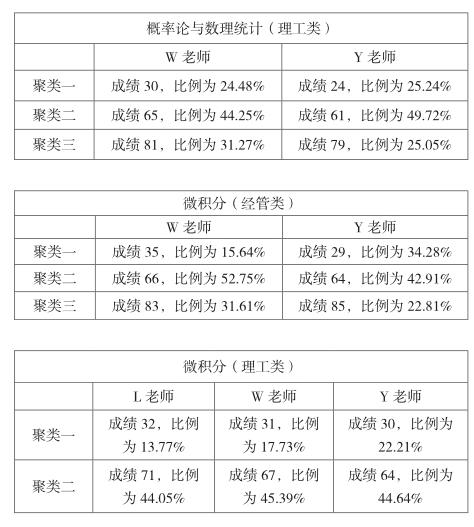

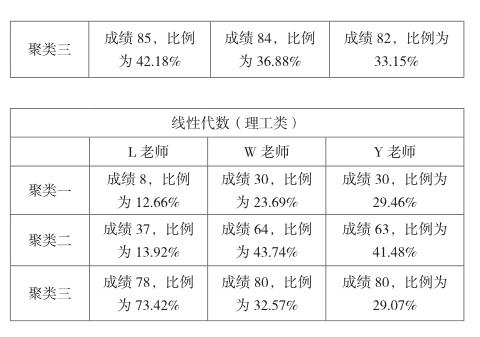
通过对不同老师相同课程的横向比较发现：每位老师的各个课程的横向比较，学生成绩的划分大致相同，且所占比例最多的聚类中心点在成绩65左右。

5 对数据分课程得出的聚类进行正态分布模型检验

从正态分布模型中看出虽然整体并不服从正态分布，现探究是否存在某一定区域内的数据服从正态分布。

将2010～2017级的概率论与数理统计（理工类）、微积分（经管类）、微积分（理工类）、线性代数（理工类）这四门不同的公共数学课程对按3类聚类进行聚类分析输出的结果再次根据各自的聚类再次进行正态分布模型检验。

从输出结果中，可以看到各个课程的每个聚类成绩都是均匀地分布在某个特定的区间内，并没有存在有很多偏离区域很大的点。同时，可以看到各个课程的成绩渐进显著性，该项值均大于0.05，即视为满足预期频数。

因此可以得出结论：各个课程聚类分析后每个聚类成绩各自服从正态分布。

6 对各个课程聚类分析后每个聚类各自再次进行K-Means聚类

经过多次的尝试，最终确定聚类数目仍为3类。

具体操作步骤如上所述，得到的输出结果如下所示：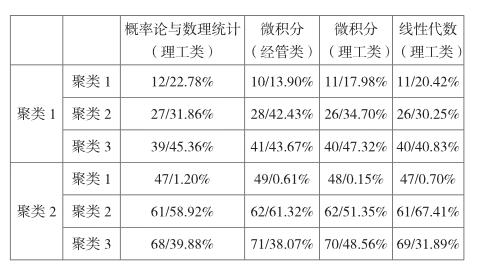

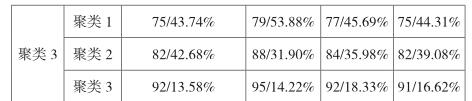
从输出结果来看，通过将各个课程的聚类分析后得到的每个聚类再次进行聚类分析，聚类中心点以及每个聚类所占比例均没有明显的差别。

7 结论

本文中共统计数据7854条：概率论与数理统计（理工类）课程学生成绩1871条，微积分（经管类）课程学生成绩1684条，微积分（理工类）学生成绩1725条，线性代数（经管类）学生成绩539条，线性代数（理工类）学生成绩2035条。

对所得数据通过正态分布模型检验得到，学生成绩并不像预计的一样服从正态分布。

对数据进行聚类分析发现：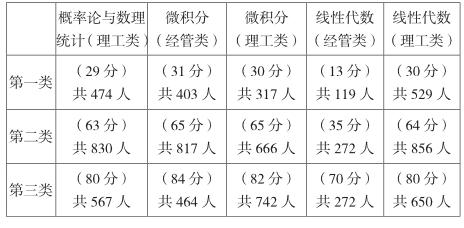

基本上每个课程的学生成绩都呈现“不及格—及格—高分”这三个成绩区间，且处于“及格”区间的人数多于其他区间。

之后，通过课程、老师、年级分类，再进行聚类分析。分析输出的结果，发现不同课程、老师、年级的学生成绩基本上刚好可以划分为“不及格—及格—高分”这三个类别。其中不及格的聚点在8～56之间，其中33为众数。及格的聚点在60～73之间，其中62、64为众数。高分的聚点在75～87之间，其中77为众数。

自2010年起到2017年的八年中，不及格学生的成绩虽有略微提高，但是变化不大。及格学生的成绩则变化较大，提升了6～7分。高分组学生的成绩比较稳定，上下浮动不大。

通过课程、老师分类，再进行聚类分析。分析输出结果显示，教师的不同对学生成绩的划分并无太大影响，不同课程对学生成绩的划分也不存在太大的影响。

鉴于通过对各个课程的正态分布模型检验看到整体虽然不服从正态分布，但通过对各个课程聚类分析后得出的聚类再次进行正态分布模型检验，发现各个聚类中的成绩是服从正态分布。

因此，对各个课程聚类分析后每个聚类各自再次进行K-Means聚类。通过输出结果可以看到聚类中心点以及每个聚类所占比例均没有明显的差别。由此可得出结论：不同班级、年级、教师之间学生成绩分布差异不明显。

综上所述，近年来，该校学生公共数学成绩60多分人数居多，80分以上高分人数相对较少。原因之一是在时间安排上，十八周课程一结束就开始考试，考试时间、科目密集，学生缺乏充足的考前复习归纳总结时间，使得学生往往考前突击复习，导致大部分学生考试成绩普遍偏低，高分相对较少；近年来学校扩招，降低了生源的准入门槛，导致学生总体素质下降，成绩出现在高分区间的数量也就相应下降；另外，学校设置计算总成绩的方法是当学生期末成绩高于50分，将平时、期中、期末成績加权平均为总成绩，导致总成绩在50～59分数段的数据缺失。

参考文献：

[1]高惠璇.应用多元统计分析[M].北京：北京大学出版社，2014：1-419.

[2]范金城，梅长林.数据分析[M].北京：科学出版社，2002：205-241.

[3]薛薇.SPSS统计分析方法及应用[M].北京：电子工业出版社，2013：1-382.

[4]李春林.应用多元统计分析[M].北京：清华大学出版社，2013：1-223.

[5]薛薇.统计分析与SPSS的应用[M].北京：中国人民大学出版社，2014.1-307.

[6]杨维忠，张甜.SPSS统计分析与行业应用案例详解[M].北京：清华大学出版社，2013：1-412.

[7]冯岩松.SPSS22.0统计分析应用教程[M].北京：清华大学出版社，2015：1-439.

[8]吴赣昌 概率论与数理统计（理工类·第五版） [M].北京：中国人民大学出版社，2017：212-217.

[9]戴维·R·安德森.商务与经济统计（第八版）[M].北京：中信出版社，2003：505.

◇责任编辑 赵丽斌◇