基于Matlab的量子密码攻击性能分析

张盛 王搏稀

（武警海警学院 浙江省宁波市 315801）

1 引言

近年来，量子信息技术发展迅速，作为量子信息学的分支之一，量子通信在理论和应用上也取得了巨大的发展成就。其最初以量子远程传态和量子稠密编码[1,2]等方案被人们所熟知，而如今，量子密钥分发和量子纠缠分发等方案也走出了实验室，逐渐开启了市场化应用的进程。另一方面，高效安全的信息传输日益受到人们的关注，安全性也成为通信性能的重要指标。正因为如此，量子通信以其“理论上的不可破译性”吸引了众多研究者和社会主体的关注。

基于无相互作用测量而研究出的反直观量子密码[3-5]，最初由Noh[5]在QKD 协议中提出，后被应用于密钥分配协议[6]中，这种反直观量子密码其中的量子态作为信息载体，永远不会通过传输信道。根据不可克隆定理，任何对量子密码窃取而产生的扰动都会被通信双方发现，反直观量子密码可以防止窃听者获得任何密钥信息。Yin 等人对Noh 协议（Noh09 协议）进行了安全性证明[7]。通过实验证明，发现这个协议属于拦截-重发攻击模式，在理想情况下是安全的，但实际的安全性却会受到暗计数率和低效的干涉仪的影响[8]。此外，窃听者可以通过发起反直观的特洛伊木马攻击[9]获得全部的关键性密钥信息以及可以通过有限计算资源方法在密钥长度较短的情况下获取部分信息[10]。

因此，虽然量子密码在理想情况下是不可破译的，但是，实际的量子密码系统由于受限于器件生产的技术水平，其内部仍然存在可被攻击者利用的安全漏洞，存在密钥泄露的风险。本文以一个典型的量子密钥分配方案[11]为例，利用Matlab 对两种针对该方案的攻击方法[9,10]进行建模分析，比较两种攻击方法的攻击性能，为量子密钥分配方案的设计提供新的研究视角。

2 基于Matlab的攻击模型

在量子密码的攻击方案性能分析中，不仅需要定性分析两种攻击方案所适用的条件，还要定量分析两种攻击方案性能临界值，两者结合，才能在进行量子攻击时制定出最优方案。所以对两种方案进行建模分析是关键环节。本文以两种针对反直观量子密码系统的攻击方案为例，详细介绍针对该方案的Matlab 攻击建模方法与定量分析。

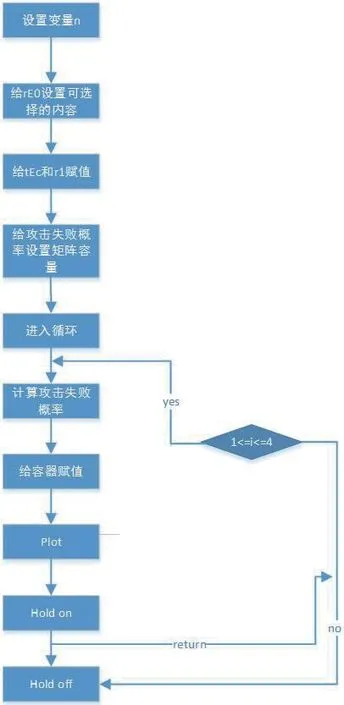
图1：有限计算资源攻击的Matlab 模型

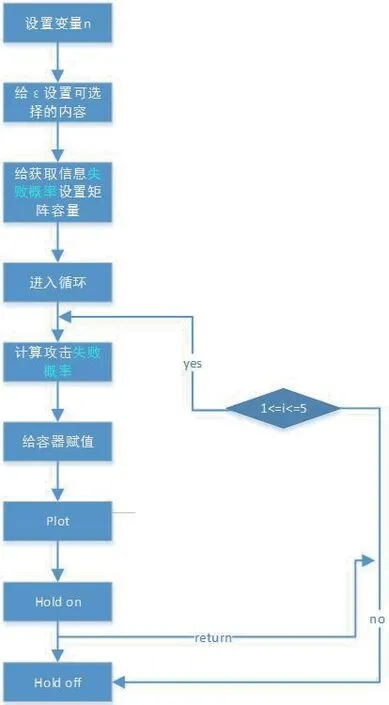
图2：特洛伊木马攻击方案的Matlab 模型

2.1 有限计算资源攻击模型[11]

有限计算资源攻击以窃听行为被发现概率为主要性能指标，其表述为：

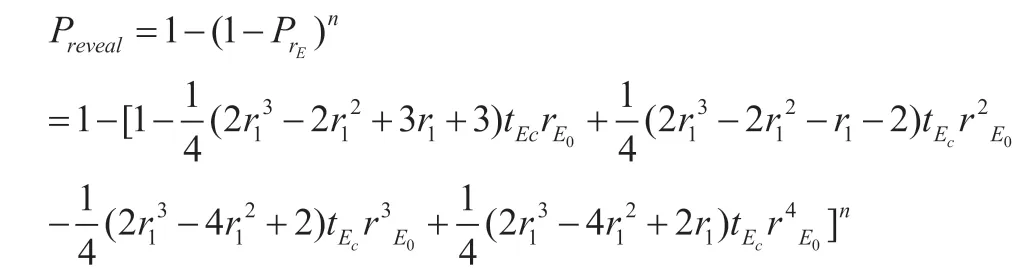
其中r1为BSE1的反射率，为Eve 端总的折射率，即BSE1累乘至再与相乘。为的反射率，n 为密钥长度，代表窃听被发现的概率。

有限计算资源攻击的Matlab 建模思路如下：首先设置好变量并设定其有效取值范围，对变化的参数进行矩阵赋值，接下来给另外两个和r1两个常量赋值。为了之后的循环运算，首先需对攻击失败的概率Preveal 设置矩阵变量，进入循环后首先计算攻击失败的概率，根据循环计算得出仿真图像，的取值由i 的值决定，当i 的取值为时，继续循环，并得出仿真图像，当i 不符合条件时，结束运算。该方案的流程图如图1所示。

2.2 特洛伊木马共攻击模型数学模型[10]

特洛伊木马攻击方案的matlab 建模思路与有限计算资源攻击有相似之处，首先设置密钥长度n 的取值，接下来给变量ε 设置可选择的内容，然后给获取信息失败的概率设置为矩阵变量，随后即可进入循环。第一步计算攻击失败的概率，接下来按照流程给矩阵变量赋值，i 的取值决定ε 的值，当时，按顺序进行循环，当i 的取值不满足循环条件时，程序结束。特洛伊木马攻击方案的matlab 模型如图2所示。

3 攻击方案的性能分析

为了更直观地比较两种攻击方案的性能优劣，须把二者的性能曲线放入同一坐标轴中，在操作过程中应注意密钥长度n 的取值范围，若密钥长度取值过小，则会出现欠拟合的情况。

如图3所示，有限计算资源攻击的性能曲线由于n 值过小，导致变化不明显，因而无法找到曲线的交点。反之，若n 的取值增大，则会出现过拟合的情况。

如图4所示，由于n 的取值过大，二者的性能偏差较大，难以找到二者的平衡点所在，即为过拟合。为了找到两种攻击方法的性能平衡点，特选取[10,100]与[1000,10000]两个n 的取样区间进行仿真，并通过判断曲线的走势，推断出平衡点的可能区间，即[100,1000]。

图3：密钥长度n 取值过小时的性能图

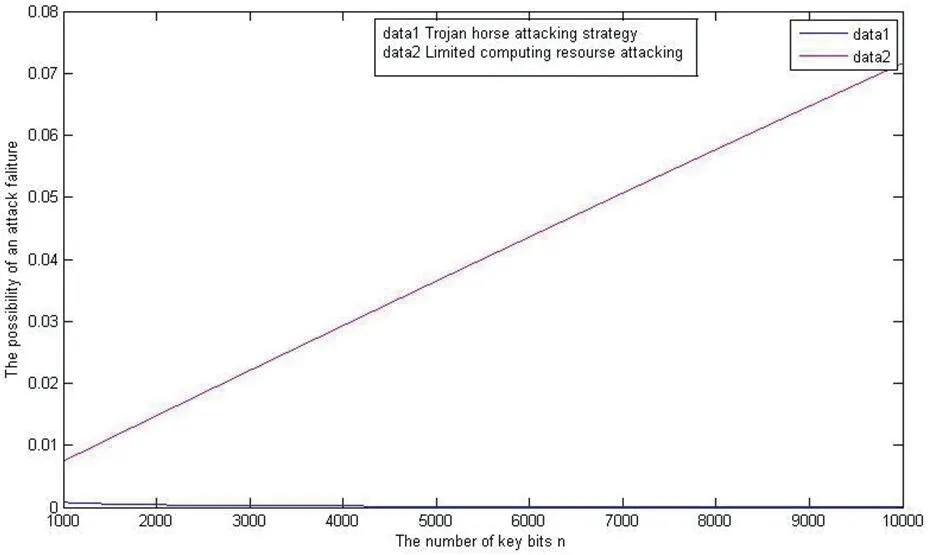
图4：密钥长度n 取值过大时的性能图

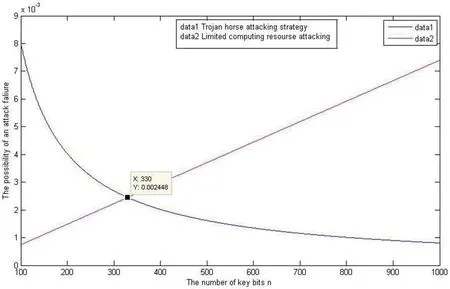
图5：两种攻击方法的性能平衡点图

如图5所示，两种攻击方法的性能曲线交于一点（即密钥长度n=330 时），验证了上述推断，该点即为平衡点。通过以上结果不难发现，有限计算资源攻击方法与特洛伊木马攻击方法二者性能的好坏取决于密钥长度。

当密钥长度n 为330 时，两者的攻击性能基本相同。当n 值小于330 时，特洛伊木马攻击方法的性能不占优，即能被窃取的密钥长度较小，窃听失败。而对于有限计算资源攻击方法而言，此时被终端发现的概率较小，性能具有明显优势，因此，若n 为[0,330]区间内的取值，宜选用有限计算资源攻击方法。

反之，当n＞330 时，有限计算资源攻击方法的性能迅速下降，而特洛伊木马攻击方法成功率增加。因此，此时宜应选择特洛伊木马攻击方法。可见两种方法各有优势，总的来说特洛伊木马攻击方案适用的范围更广，但是在实际应用中，应该根据密钥长度和实际需要进行选择。

4 小结

本文利用Matlab 对两种量子密码的攻击方案进行定量分析，为不同量子密码系统的攻击方案的性能比较提供了可靠的验证方法。但是，不同的量子攻击方案性能优劣一般很难直接比较，只要在适当的前提下，选取比较公平的衡量标准，才能实施。需要注意的是，针对量子密码的攻击方法研究目的是为了进一步弥补实际量子密码系统的技术漏洞，因此，研究量子系统的攻击方案对量子密码技术的发展具有一定推动作用。